Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Apel, Thomas
and
Matthies, Gunar
2008.
Nonconforming, Anisotropic, Rectangular Finite Elements of Arbitrary Order for the Stokes Problem.
SIAM Journal on Numerical Analysis,
Vol. 46,
Issue. 4,
p.
1867.
2010.
Die Finite‐Elemente‐Methode für Anfänger.
p.
213.
Köster, M.
Ouazzi, A.
Schieweck, F.
Turek, S.
and
Zajac, P.
2012.
New robust nonconforming finite elements of higher order.
Applied Numerical Mathematics,
Vol. 62,
Issue. 3,
p.
166.
Zhou, Xin-chen
Meng, Zhao-liang
Wang, Xiao-shan
and
Luo, Zhong-xuan
2016.
Quadratic nonconforming finite element method for 3D Stokes equations on cuboid meshes.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 31,
Issue. 1,
p.
21.
Zhou, Xinchen
Meng, Zhaoliang
and
Luo, Zhongxuan
2016.
New nonconforming finite elements on arbitrary convex quadrilateral meshes.
Journal of Computational and Applied Mathematics,
Vol. 296,
Issue. ,
p.
798.
Linke, Alexander
Matthies, Gunar
and
Tobiska, Lutz
2016.
Robust Arbitrary Order Mixed Finite Element Methods for the Incompressible Stokes Equations with pressure independent velocity errors.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 50,
Issue. 1,
p.
289.
Cangiani, Andrea
Gyrya, Vitaliy
and
Manzini, Gianmarco
2016.
The NonConforming Virtual Element Method for the Stokes Equations.
SIAM Journal on Numerical Analysis,
Vol. 54,
Issue. 6,
p.
3411.
Cangiani, Andrea
Manzini, Gianmarco
and
Sutton, Oliver J.
2016.
Conforming and nonconforming virtual element methods for elliptic problems.
IMA Journal of Numerical Analysis,
p.
drw036.
Meng, Zhaoliang
Luo, Zhongxuan
and
Zhou, Xinchen
2017.
A stable nonconforming finite element on hexahedra.
International Journal for Numerical Methods in Engineering,
Vol. 109,
Issue. 5,
p.
611.
Berrone, S.
Borio, A.
and
Manzini, G.
2018.
SUPG stabilization for the nonconforming virtual element method for advection–diffusion–reaction equations.
Computer Methods in Applied Mechanics and Engineering,
Vol. 340,
Issue. ,
p.
500.
Liu, Xin
and
Chen, Zhangxin
2019.
The nonconforming virtual element method for the Navier-Stokes equations.
Advances in Computational Mathematics,
Vol. 45,
Issue. 1,
p.
51.
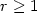 with optimal approximation properties on quadrilaterals andhexahedra. Their vector-valued versions together with a discontinuouspressure approximation of order $r-1$
with optimal approximation properties on quadrilaterals andhexahedra. Their vector-valued versions together with a discontinuouspressure approximation of order $r-1$ 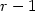 form inf-sup stable finite element pairsof order r for the Stokes problem. The well-known elements by Rannacherand Turek are recovered in the case r=1. A numerical comparison betweenconforming and nonconforming discretisations will be given. Since higherorder nonconforming discretisation on quadrilaterals and hexahedra have lessunknowns and much less non-zero matrix entries compared to correspondingconforming methods, these methods are attractive for numerical simulations.
form inf-sup stable finite element pairsof order r for the Stokes problem. The well-known elements by Rannacherand Turek are recovered in the case r=1. A numerical comparison betweenconforming and nonconforming discretisations will be given. Since higherorder nonconforming discretisation on quadrilaterals and hexahedra have lessunknowns and much less non-zero matrix entries compared to correspondingconforming methods, these methods are attractive for numerical simulations.
