Published online by Cambridge University Press: 15 August 2002
Let L be a parabolic second order differential operator on the domain $
\bar{\Pi}=\left[ 0,T\right] \times {\mathbb R}.$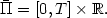 Given a function $\hat{u}:
{\mathbb R\rightarrow R}$
Given a function $\hat{u}:
{\mathbb R\rightarrow R}$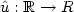 and $\hat{x}>0$
and $\hat{x}>0$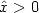 such that the support of û is
contained in $(-\infty ,-\hat{x}]$
such that the support of û is
contained in $(-\infty ,-\hat{x}]$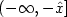 , we let $\hat{y}:\bar{\Pi}\rightarrow
{\mathbb R}$
, we let $\hat{y}:\bar{\Pi}\rightarrow
{\mathbb R}$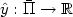 be the solution to the equation:
\[
L\hat{y}=0,\text{\quad }\hat{y}|_{\{0\}\times {\mathbb R}}=\hat{u} .
\]
be the solution to the equation:
\[
L\hat{y}=0,\text{\quad }\hat{y}|_{\{0\}\times {\mathbb R}}=\hat{u} .
\]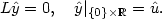 Given positive bounds $0<x_{0}<x_{1},$
Given positive bounds $0<x_{0}<x_{1},$ we seek a function u with support
in $\left[ x_{0},x_{1}\right] $
we seek a function u with support
in $\left[ x_{0},x_{1}\right] $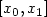 such that the corresponding solution y
satisfies:
\[
y(t,0)=\hat{y}(t,0)\quad \quad \forall t\in \left[ 0,T\right] .
\]
such that the corresponding solution y
satisfies:
\[
y(t,0)=\hat{y}(t,0)\quad \quad \forall t\in \left[ 0,T\right] .
\] We prove in this article that, under some regularity conditions on the
coefficients of L, continuous solutions are unique and dense in the sense
that $\hat{y}|_{[0,T]\times \{0\}}$
We prove in this article that, under some regularity conditions on the
coefficients of L, continuous solutions are unique and dense in the sense
that $\hat{y}|_{[0,T]\times \{0\}}$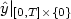 can be C0-approximated, but an
exact solution does not exist in general. This result solves the problem of almost replicating a barrier option in the
generalised Black–Scholes framework with a combination of European options,
as stated by Carr et al. in [6].
can be C0-approximated, but an
exact solution does not exist in general. This result solves the problem of almost replicating a barrier option in the
generalised Black–Scholes framework with a combination of European options,
as stated by Carr et al. in [6].