Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fridman, Emilia
Nicaise, Serge
and
Valein, Julie
2009.
Stability of second order evolution equations with time-varying delays.
IFAC Proceedings Volumes,
Vol. 42,
Issue. 14,
p.
112.
Ait Benhassi, E. M.
Ammari, K.
Boulite, S.
and
Maniar, L.
2009.
Feedback stabilization of a class of evolution equations with delay.
Journal of Evolution Equations,
Vol. 9,
Issue. 1,
p.
103.
Ning, Zhen-Hu
and
Yan, Qing-Xu
2010.
Stabilization of the wave equation with variable coefficients and a delay in dissipative boundary feedback.
Journal of Mathematical Analysis and Applications,
Vol. 367,
Issue. 1,
p.
167.
Zhang, Zai-yun
Liu, Zhen-hai
Miao, Xiu-jin
and
Chen, Yue-zhong
2010.
Stability analysis of heat flow with boundary time-varying delay effect.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 6,
p.
1878.
Fridman, Emilia
Nicaise, Serge
and
Valein, Julie
2010.
Stabilization of Second Order Evolution Equations with Unbounded Feedback with Time-Dependent Delay.
SIAM Journal on Control and Optimization,
Vol. 48,
Issue. 8,
p.
5028.
Said-Houari, Belkacem
and
Laskri, Yamina
2010.
A stability result of a Timoshenko system with a delay term in the internal feedback.
Applied Mathematics and Computation,
Vol. 217,
Issue. 6,
p.
2857.
Nicaise, Serge
and
Valein, Julie
2010.
Stabilization of second order evolution equations with unbounded feedback with delay.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 2,
p.
420.
Nicaise, Serge
Pignotti, Cristina
and
Valein, Julie
2011.
Exponential stability of the wave equation with
boundary time-varying delay.
Discrete & Continuous Dynamical Systems - S,
Vol. 4,
Issue. 3,
p.
693.
Han, Zhong-Jie
and
Xu, Gen-Qi
2011.
Dynamical behavior of networks of non-uniform Timoshenko beams system with boundary time-delay inputs.
Networks & Heterogeneous Media,
Vol. 6,
Issue. 2,
p.
297.
Henríquez, Hernán R.
Cuevas, Claudio
Rabelo, Marcos
and
Caicedo, Alejandro
2011.
Stabilization of distributed control systems with delay.
Systems & Control Letters,
Vol. 60,
Issue. 9,
p.
675.
Han, Zhong-Jie
and
Xu, Gen-Qi
2011.
Exponential stability of Timoshenko beam system with delay terms in boundary feedbacks.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 17,
Issue. 2,
p.
552.
Nicaise, Serge
2011.
Internal stabilization of a Mindlin-Timoshenko model by interior feedbacks.
Mathematical Control & Related Fields,
Vol. 1,
Issue. 3,
p.
331.
Mustafa, Muhammad I.
2011.
Uniform stability for thermoelastic systems with boundary time-varying delay.
Journal of Mathematical Analysis and Applications,
Vol. 383,
Issue. 2,
p.
490.
Kirane, Mokhtar
and
Said-Houari, Belkacem
2011.
Existence and asymptotic stability of a viscoelastic wave equation with a delay.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 62,
Issue. 6,
p.
1065.
Gerbi, Stéphane
and
Said-Houari, Belkacem
2012.
Existence and exponential stability of a damped wave equation with dynamic boundary conditions and a delay term.
Applied Mathematics and Computation,
Vol. 218,
Issue. 24,
p.
11900.
Guo, Yanni
and
Xu, Genqi
2012.
Stabilization of wave equations with boundary delays and non-collocated feedback controls.
p.
3142.
Guo, Yanni
Chen, Yunlan
Xu, Genqi
and
Zhang, Yaxuan
2012.
Exponential stabilization of variable coefficient wave equations in a generic tree with small time-delays in the nodal feedbacks.
Journal of Mathematical Analysis and Applications,
Vol. 395,
Issue. 2,
p.
727.
Shang, Ying Feng
and
Xu, Gen Qi
2012.
Stabilization of an Euler–Bernoulli beam with input delay in the boundary control.
Systems & Control Letters,
Vol. 61,
Issue. 11,
p.
1069.
Shang, Ying Feng
Xu, Gen Qi
and
Chen, Yun Lan
2012.
Stability analysis of Euler‐Bernoulli beam with input delay in the boundary control.
Asian Journal of Control,
Vol. 14,
Issue. 1,
p.
186.
Benaissa, Abbes
Benaissa, Abdelkader
and
Messaoudi, Salim. A.
2012.
Global existence and energy decay of solutions for the wave equation with a time varying delay term in the weakly nonlinear internal feedbacks.
Journal of Mathematical Physics,
Vol. 53,
Issue. 12,
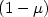 is applied over the other end. Using a simple boundary velocity feedback law, we show that the closed loop systemgenerates a C 0 group of linear operators. After a spectral analysis, we show that the closed loop system is a Riesz one, that is, there is a sequence of eigenvectors andgeneralized eigenvectors that forms a Riesz basis for the state Hilbert space.Furthermore, we show that when the weight $\mu>\frac{1}{2}$
is applied over the other end. Using a simple boundary velocity feedback law, we show that the closed loop systemgenerates a C 0 group of linear operators. After a spectral analysis, we show that the closed loop system is a Riesz one, that is, there is a sequence of eigenvectors andgeneralized eigenvectors that forms a Riesz basis for the state Hilbert space.Furthermore, we show that when the weight $\mu>\frac{1}{2}$ 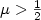 , for any time delay,we can choose a suitable feedback gain so that the closed loop system is exponentially stable. When $\mu=\frac{1}{2}$
, for any time delay,we can choose a suitable feedback gain so that the closed loop system is exponentially stable. When $\mu=\frac{1}{2}$ 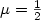 , we show that the system is at most asymptotically stable. When $\mu<\frac{1}{2}$
, we show that the system is at most asymptotically stable. When $\mu<\frac{1}{2}$ 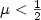 , the system is always unstable.
, the system is always unstable.