Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Khapalov, A.Y.
2009.
Micro motions of a 2-D swimming model governed by multiplicative controls.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 12,
p.
e1970.
Beauchard, Karine
2011.
Local controllability and non-controllability for a 1D wave equation with bilinear control.
Journal of Differential Equations,
Vol. 250,
Issue. 4,
p.
2064.
Beauchard, Karine
and
Morancey, Morgan
2014.
Local controllability of 1D Schrödinger equations with bilinear control and minimal time.
Mathematical Control & Related Fields,
Vol. 4,
Issue. 2,
p.
125.
Beauchard, Karine
Lange, Horst
and
Teismann, Holger
2015.
Local Exact Controllability of a One-Dimensional Nonlinear Schrödinger Equation.
SIAM Journal on Control and Optimization,
Vol. 53,
Issue. 5,
p.
2781.
Ouzahra, Mohamed
2016.
Approximate and exact controllability of a reaction–diffusion equation governed by bilinear control.
European Journal of Control,
Vol. 32,
Issue. ,
p.
32.
Jidou Khayar, M.
and
Ouzahra, M.
2020.
Partial controllability of the bilinear reaction–diffusion equation.
International Journal of Dynamics and Control,
Vol. 8,
Issue. 1,
p.
197.
Ouzahra, Mohamed
2022.
Approximate controllability of the semilinear reaction-diffusion equation governed by a multiplicative control.
Discrete & Continuous Dynamical Systems - B,
Vol. 27,
Issue. 2,
p.
1075.
Pozzoli, Eugenio
2024.
Small-time global approximate controllability of bilinear wave equations.
Journal of Differential Equations,
Vol. 388,
Issue. ,
p.
421.
 of the semilinear vibrating string that can be reached from any non-zero initial state $ (y_0, y_1) \in H^1_0 (0,1) \times L^2 (0,1)$
of the semilinear vibrating string that can be reached from any non-zero initial state $ (y_0, y_1) \in H^1_0 (0,1) \times L^2 (0,1)$ 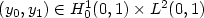 , by varying its axial load and the gain of damping, is dense in the “nonnegative” part of the subspace $ L^2 (0,1) \times \{0\} $
, by varying its axial load and the gain of damping, is dense in the “nonnegative” part of the subspace $ L^2 (0,1) \times \{0\} $ 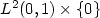 of $ L^2 (0,1) \times H^{-1} (0,1)$
of $ L^2 (0,1) \times H^{-1} (0,1)$ 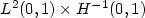 . Our main results deal with nonlinear terms which admit at most the linear growth at infinity in $ \; y \; $
. Our main results deal with nonlinear terms which admit at most the linear growth at infinity in $ \; y \; $  and satisfy certain restriction on their total impact on (0,∞) with respect to the time-variable.
and satisfy certain restriction on their total impact on (0,∞) with respect to the time-variable.