Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goncalves, J.M.
2002.
λ/sub 2/-Gain of double integrators with saturation nonlinearity.
IEEE Transactions on Automatic Control,
Vol. 47,
Issue. 12,
p.
2063.
Angeli, D.
Chitour, Y.
and
Marconi, L.
2003.
New results on robust stabilization via saturated feedback.
p.
4445.
Chitour, Y.
and
Zongli Lin
2003.
Finite gain l/sub p/ stabilization of discrete-time linear systems subject to actuator saturation: the case of p = 1.
Vol. 6,
Issue. ,
p.
5663.
Chitour, Y.
and
Zongli Lin
2003.
Finite gain l/sub p/ stabilization of discrete-time linear systems subject to actuator saturation: the case of p = 1.
IEEE Transactions on Automatic Control,
Vol. 48,
Issue. 12,
p.
2196.
Malisoff, Michael
Rifford, Ludovic
and
Sontag, Eduardo
2004.
Global Asymptotic Controllability Implies Input-to-State Stabilization.
SIAM Journal on Control and Optimization,
Vol. 42,
Issue. 6,
p.
2221.
Haijun Fang
Zongli Lin
and
Shamash, Y.
2005.
Disturbance Tolerance and Rejection of Linear Systems with Imprecise Knowledge of Actuator Input Output Characteristics.
p.
8294.
Fen Wu
Qian Zheng
and
Zongli Lin
2005.
Disturbance Attenuation for Linear Systems Subject to Actuator Saturation using Output Feedback.
p.
7546.
Angeli, D.
Chitour, Y.
and
Marconi, L.
2005.
Robust stabilization via saturated feedback.
IEEE Transactions on Automatic Control,
Vol. 50,
Issue. 12,
p.
1997.
Fang, Haijun
Lin, Zongli
and
Shamash, Yacov
2006.
Disturbance tolerance and rejection of linear systems with imprecise knowledge of actuator input output characteristics.
Automatica,
Vol. 42,
Issue. 9,
p.
1523.
Fang, H.
and
Lin, Z.
2006.
Global Practical Stabilization of Planar Linear Systems in the Presence of Actuator Saturation and Input Additive Disturbance.
IEEE Transactions on Automatic Control,
Vol. 51,
Issue. 7,
p.
1177.
Wen, Zheng
Roy, Sandip
and
Saberi, Ali
2007.
On the Disturbance Response and External Stability of a Saturating Static-Feedback-Controlled Double Integrator.
p.
4697.
Lv, Liang
and
Lin, Zongli
2008.
Analysis and design of singular linear systems under actuator saturation and disturbances.
Systems & Control Letters,
Vol. 57,
Issue. 11,
p.
904.
Forni, Fulvio
Galeani, Sergio
and
Zaccarian, Luca
2008.
Globally stabilizing quasi time-optimal control of planar saturated linear systems.
p.
883.
Lv, Liang
Lin, Zongli
and
Fang, Haijun
2008.
Analysis and Design of Switched Linear Systems in the Presence of Actuator Saturation and L2 Disturbances.
IFAC Proceedings Volumes,
Vol. 41,
Issue. 2,
p.
2490.
Wu, Fen
Zheng, Qian
and
Lin, Zongli
2009.
Disturbance attenuation by output feedback for linear systems subject to actuator saturation.
International Journal of Robust and Nonlinear Control,
Vol. 19,
Issue. 2,
p.
168.
Fang, Haijun
2010.
Global practical stabilization of third order integrator chain with actuator saturation and input additive disturbances.
p.
5222.
Bin Zhou
Guangren Duan
and
Zongli Lin
2010.
Global Stabilization of the Double Integrator System With Saturation and Delay in the Input.
IEEE Transactions on Circuits and Systems I: Regular Papers,
Vol. 57,
Issue. 6,
p.
1371.
Wang, Xu
Saberi, Ali
Stoorvogel, Anton A.
and
Grip, Håvard Fjær
2012.
Control of a chain of integrators subject to actuator saturation and disturbances.
International Journal of Robust and Nonlinear Control,
Vol. 22,
Issue. 14,
p.
1562.
Laghrouche, Salah
Harmouche, Mohamed
and
Chitour, Yacine
2012.
Target-point based path following controller for car-type vehicle using bounded feedback.
p.
562.
Saberi, Ali
Stoorvogel, Anton A.
and
Sannuti, Peddapullaiah
2012.
Internal and External Stabilization of Linear Systems with Constraints.
p.
723.
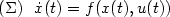 , such that there exists a feedback stabilizer k
that renders $\dot x=f(x,k(x))$
, such that there exists a feedback stabilizer k
that renders $\dot x=f(x,k(x))$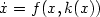 globally asymptotically
stable. Moreover, for (H,p,q) with H an output map and $1\leq
p\leq q\leq \infty$
globally asymptotically
stable. Moreover, for (H,p,q) with H an output map and $1\leq
p\leq q\leq \infty$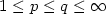 , we assume that there exists a ${\cal {K}}_{\infty}$
, we assume that there exists a ${\cal {K}}_{\infty}$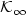 -function
α such that $\|H(x_u)\|_q\leq \alpha(\|u\|_p)$
-function
α such that $\|H(x_u)\|_q\leq \alpha(\|u\|_p)$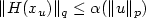 , where xu is the
maximal solution of $(\Sigma)_k \ \ \dot x(t)=f(x(t),k(x(t))+u(t))$
, where xu is the
maximal solution of $(\Sigma)_k \ \ \dot x(t)=f(x(t),k(x(t))+u(t))$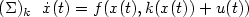 ,
corresponding to u and to the initial condition x(0)=0. Then, the
gain function $G_{(H,p,q)}$
,
corresponding to u and to the initial condition x(0)=0. Then, the
gain function $G_{(H,p,q)}$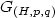 of (H,p,q) given by 14.5cm
$$
G_{(H,p,q)}(X)\stackrel{\rm def}{=}\sup_{\|u\|_p=X}\|H(x_u)\|_q,
$$
of (H,p,q) given by 14.5cm
$$
G_{(H,p,q)}(X)\stackrel{\rm def}{=}\sup_{\|u\|_p=X}\|H(x_u)\|_q,
$$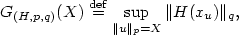 is well-defined. We call profile of k for (H,p,q) any
${\cal {K}}_{\infty}$
is well-defined. We call profile of k for (H,p,q) any
${\cal {K}}_{\infty}$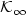 -function which is of the same order of magnitude
as $G_{(H,p,q)}$
-function which is of the same order of magnitude
as $G_{(H,p,q)}$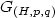 . For the double integrator subject to input saturation
and stabilized by
$k_L(x)=-(1\ 1)^Tx$
. For the double integrator subject to input saturation
and stabilized by
$k_L(x)=-(1\ 1)^Tx$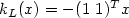 , we determine the profiles corresponding to the main
output maps. In particular, if $\sigma_0$
, we determine the profiles corresponding to the main
output maps. In particular, if $\sigma_0$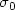 is used to denote the standard
saturation function, we show that the L2-gain from the output of the
saturation nonlinearity to u of the system $\ddot x=\sigma_0(-x-\dot x+u)$
is used to denote the standard
saturation function, we show that the L2-gain from the output of the
saturation nonlinearity to u of the system $\ddot x=\sigma_0(-x-\dot x+u)$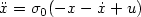 with $x(0)= \dot x(0)=0$
with $x(0)= \dot x(0)=0$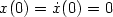 , is finite. We also provide a class of feedback
stabilizers kF that have a linear profile for (x,p,p), $1\leq p\leq \infty$
, is finite. We also provide a class of feedback
stabilizers kF that have a linear profile for (x,p,p), $1\leq p\leq \infty$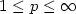 .
For instance,
we show that the L2-gains from x and $\dot x$
.
For instance,
we show that the L2-gains from x and $\dot x$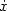 to u of the
system $\ddot x=\sigma_0(-x-\dot x-(\dot x)^3+u)$
to u of the
system $\ddot x=\sigma_0(-x-\dot x-(\dot x)^3+u)$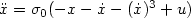 with $x(0)= \dot x(0)=0$
with $x(0)= \dot x(0)=0$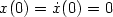 ,
are finite.
,
are finite.