Published online by Cambridge University Press: 23 January 2009
Motivated by the study of multidimensional control problems of Dieudonné-Rashevsky type, we raise the question how to understand to notion of quasiconvexity for a continuous function f with a convex body K $\subset \mathbb{R}^{nm}$ 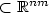 instead of the whole space $\mathbb{R}^{nm}$
instead of the whole space $\mathbb{R}^{nm}$ 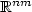 as the range of definition. In the present paper, we trace the consequences of an infinite extension of f outside K, and thus study quasiconvex functions which are allowed to take the value +∞. As an appropriate envelope, we introduce and investigate the lower semicontinuous quasiconvex envelope $f^{(qc)} (v) = {\rm sup} \{ \,g(v)\, \vert \,g : \mathbb{R}^{nm} \rightarrow \mathbb{R} \cup \{ + \infty \}$
as the range of definition. In the present paper, we trace the consequences of an infinite extension of f outside K, and thus study quasiconvex functions which are allowed to take the value +∞. As an appropriate envelope, we introduce and investigate the lower semicontinuous quasiconvex envelope $f^{(qc)} (v) = {\rm sup} \{ \,g(v)\, \vert \,g : \mathbb{R}^{nm} \rightarrow \mathbb{R} \cup \{ + \infty \}$ 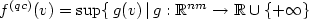 quasiconvex and lower semicontinuous, $g(v) \leq f(v) \,\,\,\,\forall v \in \mathbb{R}^{nm}\,\}.$
quasiconvex and lower semicontinuous, $g(v) \leq f(v) \,\,\,\,\forall v \in \mathbb{R}^{nm}\,\}.$ 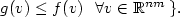 Our main result is a representation theorem for $f^{({\it qc})}$
Our main result is a representation theorem for $f^{({\it qc})}$ 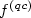 which generalizes Dacorogna's well-known theorem on the representation of the quasiconvex envelope of a finite function. The paper will be completed by the calculation of $f^{({\it qc})}$
which generalizes Dacorogna's well-known theorem on the representation of the quasiconvex envelope of a finite function. The paper will be completed by the calculation of $f^{({\it qc})}$ 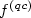 in two examples.
in two examples.