No CrossRef data available.
Article contents
On a variational problem arising in crystallography
Published online by Cambridge University Press: 14 February 2007
Abstract
We study a variational problem which was introduced by Hannon,Marcus and Mizel [ESAIM: COCV9 (2003) 145–149] todescribe step-terraces on surfaces of so-called “unorthodox” crystals.We show that there is no nondegenerate intervals on which the absolutevalue of a minimizer is $\pi/2$ 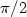 identically.
identically.
Information
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 1 , January 2007 , pp. 72 - 92
- Copyright
- © EDP Sciences, SMAI, 2007
References
Dacorogna, B. and Pfister, C.E., Wulff theorem and best constant in Sobolev inequality.
J. Math. Pures Appl.
71 (1992) 97–118.
Hannon, J., Bartelt, N.C., Swartzentruber, B.S., Hamilton, J.C. and Kellogg, G.L., Step faceting at the (001) surface of boron doped silicon.
Phys. Rev. Lett.
79 (1997) 4226–4229.
CrossRef
Hannon, J., Marcus, M. and Mizel, V.J., A variational problem modelling behavior of unorthodox silicon crystals.
ESAIM: COCV
9 (2003) 145–149.
CrossRef
Jeng, H.C. and Williams, E.D., Steps on surfaces: experiment and theory.
Surface Science Reports
34 (1999) 175–294.

