Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yamamoto, Masahiro
2009.
Carleman estimates for parabolic equations and applications.
Inverse Problems,
Vol. 25,
Issue. 12,
p.
123013.
Wu, Bin
and
Liu, Jijun
2011.
Conditional stability and uniqueness for determining two coefficients in a hyperbolic–parabolic system.
Inverse Problems,
Vol. 27,
Issue. 7,
p.
075013.
Wu, Bin
2012.
Carleman estimate for a strongly damped wave equation and applications to an inverse problem.
Mathematical Methods in the Applied Sciences,
Vol. 35,
Issue. 4,
p.
427.
Wu, Bin
and
Liu, Jijun
2012.
Determination of an unknown source for a thermoelastic system with a memory effect.
Inverse Problems,
Vol. 28,
Issue. 9,
p.
095012.
Guzmán Meléndez, Patricio
2013.
Lipschitz stability in an inverse problem for the main coefficient of a Kuramoto–Sivashinsky type equation.
Journal of Mathematical Analysis and Applications,
Vol. 408,
Issue. 1,
p.
275.
Wu, Bin
Chen, Qun
and
Wang, Zewen
2013.
Uniqueness and stability of an inverse problem for a phase field model using data from one component.
Computers & Mathematics with Applications,
Vol. 66,
Issue. 10,
p.
2126.
Wu, Bin
Yu, Jun
and
Wang, Zewen
2013.
Uniqueness and stability of an inverse kernel problem for type III thermoelasticity.
Journal of Mathematical Analysis and Applications,
Vol. 402,
Issue. 1,
p.
242.
Machida, Manabu
and
Yamamoto, Masahiro
2014.
Global Lipschitz stability in determining coefficients of the radiative transport equation.
Inverse Problems,
Vol. 30,
Issue. 3,
p.
035010.
Ainseba, Bedr'Eddine
Bendahmane, Mostafa
and
He, Yuan
2015.
Stability of conductivities in an inverse problem in the reaction-diffusion system in electrocardiology.
Networks and Heterogeneous Media,
Vol. 10,
Issue. 2,
p.
369.
Gölgeleyen, Fikret
and
Yamamoto, Masahiro
2016.
Stability for Some Inverse Problems for Transport Equations.
SIAM Journal on Mathematical Analysis,
Vol. 48,
Issue. 4,
p.
2319.
Shang, Yunxia
Zhao, Lixia
Li, Shumin
and
Ning, Wuqing
2017.
An inverse problem for Maxwell's equations in a uniaxially anisotropic medium.
Journal of Mathematical Analysis and Applications,
Vol. 456,
Issue. 2,
p.
1415.
Wu, Bin
and
Yu, Jun
2017.
Hölder stability of an inverse problem for a strongly coupled reaction-diffusion system.
IMA Journal of Applied Mathematics,
p.
hxw058.
Yuan, Ganghua
2017.
Conditional stability in determination of initial data for stochastic parabolic equations.
Inverse Problems,
Vol. 33,
Issue. 3,
p.
035014.
Gaitan, Patricia
and
Ouzzane, Hadjer
2017.
Stability result for two coefficients in a coupled hyperbolic-parabolic system.
Journal of Inverse and Ill-posed Problems,
Vol. 25,
Issue. 3,
p.
265.
Jiang, Daijun
Feng, Hui
and
Zou, Jun
2018.
Quadratic convergence of Levenberg-Marquardt method for elliptic and parabolic inverse robin problems.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 52,
Issue. 3,
p.
1085.
Abidi, Yassine
Bellassoued, Mourad
Mahjoub, Moncef
and
Zemzemi, Nejib
2018.
On the identification of multiple space dependent ionic parameters in cardiac electrophysiology modelling.
Inverse Problems,
Vol. 34,
Issue. 3,
p.
035005.
Wu, Bin
Yan, Lin
Gao, Ying
and
Chen, Qun
2018.
Carleman estimate for a linearized bidomain model in electrocardiology and its applications.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 25,
Issue. 1,
Harrach, Bastian
and
Meftahi, Houcine
2019.
Global Uniqueness and Lipschitz-Stability for the Inverse Robin Transmission Problem.
SIAM Journal on Applied Mathematics,
Vol. 79,
Issue. 2,
p.
525.
Wu, Bin
Gao, Ying
Wang, Zewen
and
Chen, Qun
2019.
Unique continuation for a reaction-diffusion system with cross diffusion.
Journal of Inverse and Ill-posed Problems,
Vol. 27,
Issue. 4,
p.
511.
Harrach, Bastian
2019.
Uniqueness and Lipschitz stability in electrical impedance tomography with finitely many electrodes.
Inverse Problems,
Vol. 35,
Issue. 2,
p.
024005.
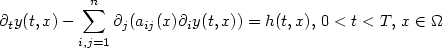 with a non-homogeneous term h, and $y\vert_{(0,T)\times\partial\Omega} = 0$
with a non-homogeneous term h, and $y\vert_{(0,T)\times\partial\Omega} = 0$ 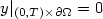 ,where $\Omega \subset\Bbb R^n$
,where $\Omega \subset\Bbb R^n$ 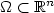 is a bounded domain. We discuss an inverse problemof determining n(n+1)/2 unknown functions a ij by $\{ \partial_{\nu}y(h_{\ell})\vert_{(0,T)\times \Gamma_0}$
is a bounded domain. We discuss an inverse problemof determining n(n+1)/2 unknown functions a ij by $\{ \partial_{\nu}y(h_{\ell})\vert_{(0,T)\times \Gamma_0}$ 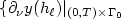 , $y(h_{\ell})(\theta,\cdot)\}_{1\le \ell\le \ell_0}$
, $y(h_{\ell})(\theta,\cdot)\}_{1\le \ell\le \ell_0}$ 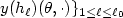 after selecting input sources $h_1, ...,h_{\ell_0}$
after selecting input sources $h_1, ...,h_{\ell_0}$  suitably, where $\Gamma_0$
suitably, where $\Gamma_0$ 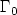 is an arbitrary subboundary, $\partial_{\nu}$
is an arbitrary subboundary, $\partial_{\nu}$ 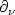 denotes the normal derivative, $0 < \theta < T$
denotes the normal derivative, $0 < \theta < T$ 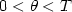 and $\ell_0 \in \Bbb N$
and $\ell_0 \in \Bbb N$ 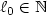 . In the case of $\ell_0 = (n+1)^2n/2$
. In the case of $\ell_0 = (n+1)^2n/2$ 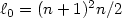 , we provethe Lipschitz stability in the inverse problem if we choose $(h_1, ...,h_{\ell_0})$
, we provethe Lipschitz stability in the inverse problem if we choose $(h_1, ...,h_{\ell_0})$ 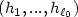 from a set ${\cal H} \subset \{ C_0^{\infty}((0,T)\times \omega)\}^{\ell_0}$
from a set ${\cal H} \subset \{ C_0^{\infty}((0,T)\times \omega)\}^{\ell_0}$ 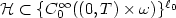 with an arbitrarily fixed subdomain $\omega \subset \Omega$
with an arbitrarily fixed subdomain $\omega \subset \Omega$  . Moreover we can take $\ell_0 = (n+3)n/2$
. Moreover we can take $\ell_0 = (n+3)n/2$ 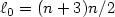 by making special choices for $h_{\ell}$
by making special choices for $h_{\ell}$ 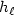 , $1 \le \ell \le \ell_0$
, $1 \le \ell \le \ell_0$ 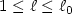 . The proof is based on a Carlemanestimate.
. The proof is based on a Carlemanestimate.
