Hostname: page-component-cb9f654ff-pvkqz Total loading time: 0 Render date: 2025-08-26T10:51:25.245Z Has data issue: false hasContentIssue false
  • English
  • Français

The Lazy Travelling Salesman Problem in $\mathbb{R}^2$

Published online by Cambridge University Press:  20 June 2007

Paz Polak  and
Gershon Wolansky
Paz Polak
Affiliation:
Weizmann Institute of Science, Rehovot, Israel.
Gershon Wolansky
Affiliation:
Department of Mathematics, Technion, Haifa 32000, Israel; gershonw@math.technion.ac.il
Get access

Abstract

We study a parameter (σ)dependent relaxation of the Travelling Salesman Problem on  $\mathbb{R}^2$ 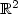.The relaxed problem is reduced to the Travelling Salesman Problemas $\sigma\rightarrow$ 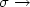0. For increasing σ it is also anordered clustering algorithm for a set of points in $\mathbb{R}^2$ 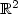.A dual formulation is introduced, which reduces the problem to aconvex optimization, provided the minimizer is in the domain ofconvexity of the relaxed functional. It is shown that this lastcondition is generically satisfied, provided σ is largeenough.

Keywords

Travelling Salesman ProblemLegendre-Fenchel transform

Information

Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 3 , July 2007 , pp. 538 - 552
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

A.J. Abrantes and J.S. Marques, Unified approach to snakes, elastic nets and Kohonen maps, in Proceeding ICASSP IEEE International Conference on Acoustics Speech Signal Process (1995) 3427–3430.
L. Cohen, On active contour models and balloons. CVGIP, Image Underst. 52 (1991) 211–218.
Durbin, R. and Willshaw, D., An analogue approach to the travelling salesman problem using an elastic net method. Nature 326 (1987) 681–691. CrossRef
Gilson, S.J. and Damper, R.I., An empirical comparison of neural techniques for edge linking of images. Neural Comput. Appl. 6 (1997) 64–78 (Historical Archive). CrossRef
Gurewitz, E., Rose, K. and Fox, G.C., Constrained clustering as an optimization method. IEEE Trans. Pattern Anal. Machine Intelligence 15 (1993) 785–794.
J.B. Hiriart-Urruty and C. Lemarèchal, Convex Analysis and Minimization Algorithms II, Grundlehren der Mathematischen Wissenschaften 306, Chap. 10. Springer-Verlag (1993).
T. Kohonen, Self-Organizing Maps, Springer Series in Information Sciences 30. Springer-Verlag (1997).
Skyum, S., A simple algorithm for computing the smallest enclosing circle. Process. Lett. 37 (1991) 121–125. CrossRef
Szeliski, R., Durbin, R. and Yuille, A., An analysis of the elastic net approach to the travelling salesman problem. Neural Comput. 1 (1989) 348–358.
Tsafrir, D., Tsafrir, I., Ein-Dor, L., Zuk, O., Notterman, D.A. and Domany, E., Sorting points into neighborhoods (spin): data analysis and visualization by ordering distance matrices. Bioinformatics 21 (2005) 2301–2308. CrossRef
E. Welzl, Smallest enclosing disks (balls) and ellipsoids, in New Results and New Trends in Computer Science, H. Maurer Ed., Lect. Notes Comput. Sci. (1991) 359–370.
C. Williams, Combining deformable models and neural networks for hand-pronted digit recognition. Ph.D. thesis, University of Toronto (1994).
A. Witkin, M. Kass and D. Terzopoulos, Snakes: Active contour models. First International Conference on Computer Vision (1987).