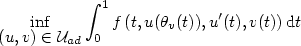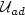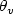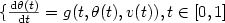Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carlier, Guillaume
and
Tahraoui, Rabah
2008.
On some optimal control problems governed by a state equation with memory.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 14,
Issue. 4,
p.
725.
Carlier, Guillaume
and
Tahraoui, Rabah
2010.
Hamilton-Jacobi-Bellman equations for the optimal control of a state equation with memory.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 3,
p.
744.
Bonnans, Joseph Frédéric
and
Sánchez Fernández de la Vega, Constanza
2010.
Optimal Control of State Constrained Integral Equations.
Set-Valued and Variational Analysis,
Vol. 18,
Issue. 3-4,
p.
307.
Buttazzo, G.
Carlier, G.
and
Tahraoui, R.
2010.
On Some Systems Controlled by the Structure of Their Memory.
SIAM Journal on Control and Optimization,
Vol. 48,
Issue. 8,
p.
5241.