Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
De Maio, U.
Gaudiello †, A.
and
Lefter ‡, C.
2004.
Optimal control for a parabolic problem in a domain with highly oscillating boundary.
Applicable Analysis,
Vol. 83,
Issue. 12,
p.
1245.
DE MAIO, U.
DURANTE, T.
and
MEL'NYK, T. A.
2005.
ASYMPTOTIC APPROXIMATION FOR THE SOLUTION TO THE ROBIN PROBLEM IN A THICK MULTI-LEVEL JUNCTION.
Mathematical Models and Methods in Applied Sciences,
Vol. 15,
Issue. 12,
p.
1897.
De Maio, U.
and
Mel'nyk, T. A.
2005.
Homogenization of the Neumann problem in thick multi‐structures of type 3 : 2 : 2.
Mathematical Methods in the Applied Sciences,
Vol. 28,
Issue. 7,
p.
865.
GAUDIELLO, ANTONIO
and
ZAPPALE, ELVIRA
2006.
JUNCTION IN A THIN MULTIDOMAIN FOR A FOURTH ORDER PROBLEM.
Mathematical Models and Methods in Applied Sciences,
Vol. 16,
Issue. 12,
p.
1887.
Amirat, Youcef
Bodart, Olivier
Maio, Umberto De
and
Gaudiello, Antonio
2007.
Asymptotic approximation of the solution of Stokes equations in a domain with highly oscillating boundary.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 53,
Issue. 2,
p.
135.
BLANCHARD, DOMINIQUE
GAUDIELLO, ANTONIO
and
MOSSINO, JACQUELINE
2007.
HIGHLY OSCILLATING BOUNDARIES AND REDUCTION OF DIMENSION: THE CRITICAL CASE.
Analysis and Applications,
Vol. 05,
Issue. 02,
p.
137.
Blanchard, Dominique
Gaudiello, Antonio
and
Griso, Georges
2007.
Junction of a periodic family of elastic rods with a thin plate. Part II.
Journal de Mathématiques Pures et Appliquées,
Vol. 88,
Issue. 2,
p.
149.
Mel'nyk, Taras A.
2008.
Homogenization of a boundary‐value problem with a nonlinear boundary condition in a thick junction of type 3:2:1.
Mathematical Methods in the Applied Sciences,
Vol. 31,
Issue. 9,
p.
1005.
Blanchard, Dominique
Gaudiello, Antonio
and
Mel'nyk, Taras A.
2008.
Boundary Homogenization and Reduction of Dimension in a Kirchhoff–Love Plate.
SIAM Journal on Mathematical Analysis,
Vol. 39,
Issue. 6,
p.
1764.
Moussa, Abdelaziz Aït
and
Zlaïji, Loubna
2012.
Dimension reduction and homogenization of random degenerate operators. Part I.
LMS Journal of Computation and Mathematics,
Vol. 15,
Issue. ,
p.
1.
Amirat, Youcef
Bodart, Olivier
De Maio, Umberto
and
Gaudiello, Antonio
2013.
Effective boundary condition for Stokes flow over a very rough surface.
Journal of Differential Equations,
Vol. 254,
Issue. 8,
p.
3395.
Klevtsovs’kyi, A. V.
and
Mel’nyk, T. A.
2014.
Asymptotic Expansion of the Solution of an Elliptic Boundary-Value Problem in a Thin Cascade Domain.
Journal of Mathematical Sciences,
Vol. 198,
Issue. 3,
p.
303.
De Maio, U.
Faella, L.
and
Perugia, C.
2014.
Optimal control problem for an anisotropic parabolic problem in a domain with very rough boundary.
Ricerche di Matematica,
Vol. 63,
Issue. 2,
p.
307.
De Maio, U.
Faella, L.
and
Perugia, C.
2015.
Optimal control for a second-order linear evolution problem in a domain with oscillating boundary.
Complex Variables and Elliptic Equations,
Vol. 60,
Issue. 10,
p.
1392.
Mel'nyk, Taras A.
2015.
Asymptotic approximation for the solution to a semi-linear parabolic problem in a thick junction with the branched structure.
Journal of Mathematical Analysis and Applications,
Vol. 424,
Issue. 2,
p.
1237.
De Maio, Umberto
K. Nandakumaran, Akamabadath
and
Perugia, Carmen
2015.
Exact internal controllability for the wave equation in a domain with oscillating boundary with Neumann boundary condition.
Evolution Equations & Control Theory,
Vol. 4,
Issue. 3,
p.
325.
Klevtsovskiy, A.V.
and
Mel’nyk, T.A.
2016.
Asymptotic expansion for the solution to a boundary-value problem in a thin cascade domain with a local joint.
Asymptotic Analysis,
Vol. 97,
Issue. 3-4,
p.
265.
Aiyappan, S.
and
Nandakumaran, A. K.
2017.
Optimal control problem in a domain with branched structure and homogenization.
Mathematical Methods in the Applied Sciences,
Vol. 40,
Issue. 8,
p.
3173.
Keller, Laura Gioia Andrea
2017.
Homogenization and concentrated capacity for the heat equation with two kinds of microstructures: uniform cases.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 196,
Issue. 3,
p.
791.
Aiyappan, S.
Nandakumaran, A. K.
and
Prakash, Ravi
2018.
Generalization of unfolding operator for highly oscillating smooth boundary domains and homogenization.
Calculus of Variations and Partial Differential Equations,
Vol. 57,
Issue. 3,
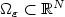 (N ≥ 2). The multidomain ΩE is composed of two domains. The first one is a plate which becomes asymptotically flat, with thickness hE in the x N direction, as ε → 0. The second one is a “forest" of cylinders distributed with ε-periodicity in the first N - 1 directions on the upper side of the plate. Each cylinder has a small cross section of size ε and fixed height (for the case N=3, see the figure). We identify the limit problem, under the assumption: ${\lim_{\varepsilon\rightarrow 0} {\varepsilon^p\over h_\varepsilon}=0}$
(N ≥ 2). The multidomain ΩE is composed of two domains. The first one is a plate which becomes asymptotically flat, with thickness hE in the x N direction, as ε → 0. The second one is a “forest" of cylinders distributed with ε-periodicity in the first N - 1 directions on the upper side of the plate. Each cylinder has a small cross section of size ε and fixed height (for the case N=3, see the figure). We identify the limit problem, under the assumption: ${\lim_{\varepsilon\rightarrow 0} {\varepsilon^p\over h_\varepsilon}=0}$ 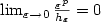 . After rescaling the equation, with respect to hE, on the plate, we prove that, in the limit domain corresponding to the “forest" of cylinders, the limit problem identifies with a diffusion operator with respect to x N , coupled with an algebraic system. Moreover, the limit solution is independent of x N in the rescaled plate and meets a Dirichlet transmission condition between the limit domain of the “forest" of cylinders and the upper boundary of the plate.
. After rescaling the equation, with respect to hE, on the plate, we prove that, in the limit domain corresponding to the “forest" of cylinders, the limit problem identifies with a diffusion operator with respect to x N , coupled with an algebraic system. Moreover, the limit solution is independent of x N in the rescaled plate and meets a Dirichlet transmission condition between the limit domain of the “forest" of cylinders and the upper boundary of the plate.

