No CrossRef data available.
Article contents
Higher-order phase transitions with line-tension effect
Published online by Cambridge University Press: 23 April 2010
Abstract
The behavior of energy minimizers at the boundary of the domain is of great importance in the Van de Waals-Cahn-Hilliard theory for fluid-fluid phase transitions, since it describes the effect of the container walls on the configuration of the liquid. This problem, also known as the liquid-drop problem, was studied by Modica in [Ann. Inst. Henri Poincaré, Anal. non linéaire 4 (1987) 487–512], and in a different form by Alberti et al. in [Arch. Rational Mech. Anal. 144 (1998) 1–46] for a first-order perturbation model.This work shows that using a second-order perturbation Cahn-Hilliard-type model, the boundary layer is intrinsically connected with the transition layer in the interior of the domain. Precisely, considering the energies
$\[{\cal F}_{\varepsilon}(u) := \varepsilon^{3} \int_{\Omega} |D^{2}u|^{2} + \frac{1}{\varepsilon} \int_{\Omega} W (u) + \lambda_{\varepsilon} \int_{\partial \Omega} V(Tu),\]$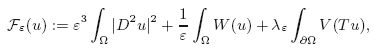
where u is a scalar density function and W and V are double-well potentials, the exact scaling law is identified in the critical regime, when $\varepsilon\lambda_{\varepsilon}^{\frac{2}{3}} \sim 1$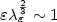 .
.
Keywords
Information
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 3 , July 2011 , pp. 603 - 647
- Copyright
- © EDP Sciences, SMAI, 2010

