Given a one-parameter family $\{g_\lambda\colon\lambda\in [a,b]\}$ 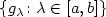of semi Riemannian metrics on ann-dimensional manifold M, a family of time-dependent potentials $\{ V_\lambda\colon \lambda\in [a,b]\}$ 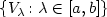and a family $\{\sigma_\lambda\colon \lambda\in [a,b]\} $ 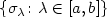of trajectories connecting two points of the mechanical system defined by $(g_\lambda, V_\lambda)$ 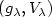, we show that there are trajectories bifurcating from the trivial branch $\sigma_\lambda$ 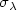if the generalized Morse indices $\mu(\sigma_a)$ 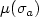and $\mu(\sigma_b)$ 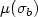are different. If the data are analytic we obtain estimates for the number of bifurcation points on the branch and, in particular, for the number of strictly conjugate points along a trajectory using an explicit computation of the Morse index inthe case of locally symmetric spaces and a comparison principle of Morse Schöenberg type.