Hostname: page-component-5b777bbd6c-5mwv9 Total loading time: 0 Render date: 2025-06-19T15:33:10.436Z Has data issue: false hasContentIssue false
  • English
  • Français

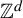Topological structure of isolated points in the space of $\mathbb {Z}^d$-shifts

Part of: Topological dynamics

Published online by Cambridge University Press:  18 June 2025

SILVÈRE GANGLOFF  and
ALONSO NÚÑEZ
SILVÈRE GANGLOFF*
Affiliation:
Independent researcher, Palma de Mallorca, Spain
ALONSO NÚÑEZ
Affiliation:
Institut de mathématiques de Toulouse, 1R3, Université Paul Sabatier, 118 Route de Narbonne, 31400 Toulouse, France Instituto de Ingeniería Matemática y Computacional, Pontificia Universidad Católica de Chile, Santiago, Chile (e-mail: alonso.herrera_nunez@math.univ-toulouse.fr)
*
e-mail: sfgangloff@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

R. Pavlov and S. Schmieding [On the structure of generic subshifts. Nonlinearity 36 (2023), 4904–4953] recently provided some results about generic 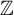$\mathbb {Z}$-shifts, which rely mainly on an original theorem stating that isolated points form a residual set in the space of 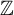$\mathbb {Z}$-shifts such that all other residual sets must contain it. As a direction for further research, they pointed towards genericity in the space of 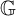$\mathbb {G}$-shifts, where 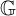$\mathbb {G}$ is a finitely generated group. In the present text, we approach this for the case of 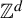$\mathbb {Z}^d$-shifts, where 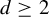$d \ge 2$. As it is usual, multidimensional dynamical systems are much more difficult to understand. In light of the result of R. Pavlov and S. Schmieding, it is natural to begin with a better understanding of isolated points. We prove here a characterization of such points in the space of 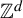$\mathbb {Z}^d$-shifts, in terms of the natural notion of maximal subsystems that we also introduce in this article. From this characterization, we recover the result of R. Pavlov and S. Schmieding for 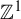$\mathbb {Z}^1$-shifts. We also prove a series of results that exploit this notion. In particular, some transitivity-like properties can be related to the number of maximal subsystems. Furthermore, we show that the Cantor–Bendixon rank of the space of 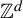$\mathbb {Z}^d$-shifts is infinite for 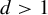$d>1$, while for 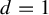$d=1$, it is known to be equal to one.

Keywords

shift spacesgeneric propertiesmultidimensional dynamical systemsCantor–Bendixson rank

MSC classification

Primary: 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 33
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akin, E., Glasner, E. and Weiss, B.. Generically there is but one self homeomorphism of the Cantor set. Trans. Amer. Math. Soc. 360 (2006), 3613–3630.10.1090/S0002-9947-08-04450-4CrossRefGoogle Scholar
Akin, E., Hurley, M. and Kennedy, J.. Dynamics of topologically generic homeomorphisms. Mem. Amer. Math. Soc. 164 (2003).Google Scholar
Berger, R.. The undecidability of the domino problem. Mem. Amer. Math. Soc. 1 (1996).Google Scholar
Bezugly, S., Dooley, A. and Kwiatkowski, J.. Topologies on the group of homeomorphisms of a cantor set. Topol. Methods Nonlinear Anal. 27(2) (2006), 299–331.Google Scholar
Callard, A. and de Menibus, B. H.. The aperiodic Domino problem in higher dimension. Proc. 39th Int. Symp. on Theoretical Aspects of Computer Science (STACS 2022) (Leibniz International Proceedings in Informatics (LIPIcs), 219). Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Wadern, 2022, pp. 19:1–19:15.Google Scholar
Doucha, M.. Strong topological Rokhlin property, shadowing, and symbolic dynamics of countable groups. J. Eur. Math. Soc. doi:10.4171/JEMS/1584. Published online 18 December 2024.CrossRefGoogle Scholar
Durand, B., Romashchenko, A. and Shen, A.. Effective closed subshifts in 1D can be implemented in 2D. Fields of Logic and Computation (Lecture Notes in Computer Science, 6300). Ed. A. Blass, N. Dershowitz and W. Reisig. Springer, Berlin, 2010, pp. 208–226.10.1007/978-3-642-15025-8_12CrossRefGoogle Scholar
Frisch, J. and Tamuz, O.. Symbolic dynamics on amenable groups: the entropy of generic shifts. Ergod. Th. & Dynam. Sys. 37 (2017), 1187–1210.10.1017/etds.2015.84CrossRefGoogle Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1(1) (1967), 1–49.10.1007/BF01692494CrossRefGoogle Scholar
Gangloff, S.. Characterizing entropy dimensions of minimal multidimensional shifts of finite type. Discrete Contin. Dyn. Syst. 42 (2022), 931–988.10.3934/dcds.2021143CrossRefGoogle Scholar
Gangloff, S. and Sablik, M.. Quantified block gluing for multidimensional SFT: aperiodicity and entropy. J. Anal. Math. 144 (2021), 21–118.10.1007/s11854-021-0172-5CrossRefGoogle Scholar
Glasner, E.. The topological Rohlin property and topological entropy. Amer. J. Math. 123 (2001), 1055–1070.10.1353/ajm.2001.0039CrossRefGoogle Scholar
Halmos, P.. Approximation theories for measure preserving transformations. Trans. Amer. Math. Soc. 55 (1944), 1–18.10.1090/S0002-9947-1944-0009703-4CrossRefGoogle Scholar
Halmos, P.. In general a measure preserving transformation is mixing. Ann. of Math. (2) 45 (1944), 786–792.10.2307/1969304CrossRefGoogle Scholar
Halmos, P.. Lectures on Ergodic Theory. Chelsea Publishing Co., New York, 1960.Google Scholar
Hochman, M.. Genericity in topological dynamics. Ergod. Th. & Dynam. Sys. 28 (2008), 125–165.10.1017/S0143385707000521CrossRefGoogle Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. (2) 171 (2010), 2011–2038.10.4007/annals.2010.171.2011CrossRefGoogle Scholar
Kechris, A. S. and Rosendal, C.. Turbulence, amalgamation and generic automorphisms of homogeneous structures. Proc. Lond. Math. Soc. (3) 94 (2007), 302–350.10.1112/plms/pdl007CrossRefGoogle Scholar
Oxtoby, J. and Ulam, S.. Measure-preserving homeomorphisms and metrical transitivity. Ann. of Math. (2) 138 (1941), 874–920.10.2307/1968772CrossRefGoogle Scholar
Pavlov, R. and Schmieding, S.. On the structure of generic subshifts. Nonlinearity 36 (2023), 4904–4953.10.1088/1361-6544/acea25CrossRefGoogle Scholar
Robinson, R.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.10.1007/BF01418780CrossRefGoogle Scholar
Rohlin, V.. A “general” measure-preserving transformation is not mixing. Dokl. Akad. Nauk 60 (1948), 349–351.Google Scholar
Rudolph, D.. ${\times}2$ and ${\times}3$ invariant measures and entropy. Ergod. Th. & Dynam. Sys. 10(2) (1990), 395–406.10.1017/S0143385700005629CrossRefGoogle Scholar
Sigmund, K.. On the prevalence of zero entropy. Israel J. Math. 10 (1971), 281–288.10.1007/BF02771645CrossRefGoogle Scholar