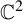Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Hénon, Julia Xénelkis
2024.
Hénon Maps: A List of Open Problems.
Arnold Mathematical Journal,
Vol. 10,
Issue. 4,
p.
585.
HIRONAKA, YUKI
and
ISHII, YUTAKA
2025.
Symbolic dynamics for Hénon maps near the boundary of the horseshoe locus.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 1,
p.
140.
Dujardin, Romain
and
Lyubich, Mikhail
2025.
Structure of hyperbolic polynomial automorphisms of C2${\mathbb {C}^2}$ with disconnected Julia sets.
Proceedings of the London Mathematical Society,
Vol. 130,
Issue. 6,