Article contents
There are no deviations for the ergodic averages of Giulietti–Liverani horocycle flows on the two-torus
Published online by Cambridge University Press: 18 March 2021
Abstract
We show that the ergodic integrals for the horocycle flow on the two-torus associated by Giulietti and Liverani with an Anosov diffeomorphism either grow linearly or are bounded; in other words, there are no deviations. For this, we use the topological invariance of the Artin–Mazur zeta function to exclude resonances outside the open unit disc. Transfer operators acting on suitable spaces of anisotropic distributions and their Ruelle determinants are the key tools used in the proof. As a bonus, we show that for any 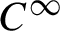 $C^\infty $ Anosov diffeomorphism F on the two-torus, the correlations for the measure of maximal entropy and
$C^\infty $ Anosov diffeomorphism F on the two-torus, the correlations for the measure of maximal entropy and 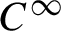 $C^\infty $ observables decay with a rate strictly smaller than
$C^\infty $ observables decay with a rate strictly smaller than 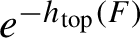 $e^{-h_{\mathrm {top}}(F)}$. We compare our results with very recent related work of Forni.
$e^{-h_{\mathrm {top}}(F)}$. We compare our results with very recent related work of Forni.
MSC classification
Information
- Type
- Original Article
- Information
- Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 500 - 513
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by


