Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Griesmer, John T.
2012.
Sumsets of dense sets and sparse sets.
Israel Journal of Mathematics,
Vol. 190,
Issue. 1,
p.
229.
LIMA, YURI
2012.
ℤd-actions with prescribed topological and ergodic properties.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 1,
p.
191.
OPROCHA, PIOTR
and
ZHANG, GUOHUA
2014.
On local aspects of topological weak mixing, sequence entropy and chaos.
Ergodic Theory and Dynamical Systems,
Vol. 34,
Issue. 5,
p.
1615.
Host, Bernard
Kra, Bryna
and
Maass, Alejandro
2016.
Variations on topological recurrence.
Monatshefte für Mathematik,
Vol. 179,
Issue. 1,
p.
57.
Bergelson, V.
and
Leibman, A.
2018.
IPr⁎-recurrence and nilsystems.
Advances in Mathematics,
Vol. 339,
Issue. ,
p.
642.
FRĄCZEK, KRZYSZTOF
KANIGOWSKI, ADAM
and
LEMAŃCZYK, MARIUSZ
2022.
Prime number theorem for regular Toeplitz subshifts.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 4,
p.
1446.
BULINSKI, KAMIL
and
FISH, ALEXANDER
2022.
Reconstructing a minimal topological dynamical system from a set of return times.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 9,
p.
2723.
PAVLOV, RONNIE
2025.
Minimal zero entropy subshifts can be unrestricted along any sparse set.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 2,
p.
566.

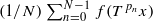 fail to converge on a residual set in
fail to converge on a residual set in 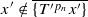 .
.