Article contents
Skinning measures in negative curvature and equidistribution of equidistant submanifolds
Published online by Cambridge University Press: 30 April 2013
Abstract
Let 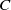 $C$ be a locally convex closed subset of a negatively curved Riemannian manifold
$C$ be a locally convex closed subset of a negatively curved Riemannian manifold 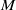 $M$. We define the skinning measure
$M$. We define the skinning measure 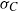 ${\sigma }_{C} $ on the outer unit normal bundle to
${\sigma }_{C} $ on the outer unit normal bundle to 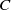 $C$ in
$C$ in 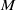 $M$ by pulling back the Patterson–Sullivan measures at infinity, and give a finiteness result for
$M$ by pulling back the Patterson–Sullivan measures at infinity, and give a finiteness result for 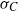 ${\sigma }_{C} $, generalizing the work of Oh and Shah, with different methods. We prove that the skinning measures, when finite, of the equidistant hypersurfaces to
${\sigma }_{C} $, generalizing the work of Oh and Shah, with different methods. We prove that the skinning measures, when finite, of the equidistant hypersurfaces to 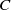 $C$ equidistribute to the Bowen–Margulis measure
$C$ equidistribute to the Bowen–Margulis measure 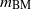 ${m}_{\mathrm{BM} } $ on
${m}_{\mathrm{BM} } $ on 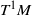 ${T}^{1} M$, assuming only that
${T}^{1} M$, assuming only that  ${m}_{\mathrm{BM} } $ is finite and mixing for the geodesic flow. Under additional assumptions on the rate of mixing, we give a control on the rate of equidistribution.
${m}_{\mathrm{BM} } $ is finite and mixing for the geodesic flow. Under additional assumptions on the rate of mixing, we give a control on the rate of equidistribution.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Cambridge University Press
References
- 9
- Cited by

