Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lopes, Artur O.
1989.
The Dimension Spectrum of the Maximal Measure.
SIAM Journal on Mathematical Analysis,
Vol. 20,
Issue. 5,
p.
1243.
Lopes, A O
1990.
Entropy and large deviation.
Nonlinearity,
Vol. 3,
Issue. 2,
p.
527.
Przytycki, Feliks
1990.
On the Perron-Frobenius-ruelle operator for rational maps on the riemann sphere and for Hölder continuous functions.
Boletim da Sociedade Brasileira de Matemática,
Vol. 20,
Issue. 2,
p.
95.
Denker, M
and
Urbanski, M
1991.
On Sullivan's conformal measures for rational maps of the Riemann sphere.
Nonlinearity,
Vol. 4,
Issue. 2,
p.
365.
Agnes, C.
and
Rasetti, M.
1991.
Undecidability of the word problem and chaos in symbolic dynamics.
Il Nuovo Cimento B Series 11,
Vol. 106,
Issue. 8,
p.
879.
Denker, M
and
Urbanski, M
1991.
Ergodic theory of equilibrium states for rational maps.
Nonlinearity,
Vol. 4,
Issue. 1,
p.
103.
Denker, Manfred
and
Urbański, Mariusz
1992.
Ergodic Theory and Related Topics III.
Vol. 1514,
Issue. ,
p.
90.
Agnes, Corrado
and
Rasetti, Mario
1995.
Undecidability and chaos in word-coded symbolic dynamics.
Chaos, Solitons & Fractals,
Vol. 5,
Issue. 2,
p.
161.
Urbański, Mariusz
2003.
Measures and dimensions in conformal dynamics.
Bulletin of the American Mathematical Society,
Vol. 40,
Issue. 3,
p.
281.
Hoffman, Christopher
2009.
Encyclopedia of Complexity and Systems Science.
p.
4983.
Hoffman, Christopher
2009.
Ergodic Theory.
p.
201.
Dinh, Tien-Cuong
and
Sibony, Nessim
2010.
Holomorphic Dynamical Systems.
Vol. 1998,
Issue. ,
p.
165.
Hoffman, Christopher
2012.
Mathematics of Complexity and Dynamical Systems.
p.
783.
Mihailescu, Eugen
2012.
On some coding and mixing properties for a class of chaotic systems.
Monatshefte für Mathematik,
Vol. 167,
Issue. 2,
p.
241.
Mihailescu, Eugen
2013.
Higher dimensional expanding maps and toral extensions.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 10,
p.
3467.
Szostakiewicz, Michał
Urbański, Mariusz
and
Zdunik, Anna
2015.
Fine inducing and equilibrium measures for rational functions of the Riemann sphere.
Israel Journal of Mathematics,
Vol. 210,
Issue. 1,
p.
399.

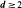 has a unique invariant probability ƒ
has a unique invariant probability ƒ . In this paper we prove that there exists
. In this paper we prove that there exists 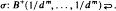 .
.