No CrossRef data available.
Article contents
On non-tameness of the Ellis semigroup
Published online by Cambridge University Press: 30 June 2025
Abstract
A tame dynamical system can be characterized by the cardinality of its enveloping (or Ellis) semigroup. Indeed, this cardinality is that of the power set of the continuum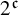 
$2^{\mathfrak c}$ if the system is non-tame. The semigroup admits a minimal bilateral ideal and this ideal is a union of isomorphic copies of a group 
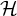$\mathcal H$, called the structure group. For almost automorphic systems, the cardinality of 
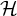$\mathcal H$ is at most 
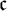${\mathfrak c}$ that of the continuum. We show a partial converse of this which holds for minimal systems for which the Ellis semigroup of their maximal equicontinuous factor acts freely, namely that the cardinality of 
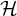$\mathcal H$ is 
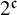$2^{{\mathfrak c}}$ if the proximal relation is not transitive and the subgroup generated by products 
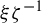$\xi \zeta ^{-1}$ of singular points 
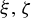$\xi ,\zeta $ in the maximal equicontinuous factor is not open. This refines the above statement about non-tame Ellis semigroups, as it locates a particular algebraic component of the latter which has such a large cardinality.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
References
Aujogue, J.-B., Barge, M., Kellendonk, J. and Lenz, D.. Equicontinuous factors, the proximal relation and Ellis semigroup for Delone sets. Mathematics of Aperiodic Order (Progress in Mathematics, 309). Ed. J. Kellendonk, D. Lent and J. Savinien. Birkhäuser/Springer, Basel, 2015, pp. 137–194.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and Their Extensions (North-Holland Mathematics Studies, 153). North-Holland Publishing Co., Amsterdam, 1988; (Notas de Matemática [Mathematical Notes], 122).Google Scholar
Barge, M. and Kellendonk, J.. The proximal relation and pure point spectrum for tiling dynamical systems. Michigan Math. J. 64(4) (2013), 793–822.Google Scholar
Ellis, R.. The Veech structure theorem. Trans. Amer. Math. Soc. 186 (1973), 203–218.CrossRefGoogle Scholar
Fuhrmann, G., Kellendonk, J. and Yassawi, R.. Tame or wild Toeplitz shifts. Ergod. Th. & Dynam. Sys. 44 (2024), 1379–1417.CrossRefGoogle Scholar
Glasner, E.. Enveloping semigroups in topological dynamics. Topology Appl. 154(11) (2007), 2344–2363.CrossRefGoogle Scholar
Glasner, E.. The structure of tame minimal dynamical systems for general groups. Invent. Math. 211(1) (2018), 213–244.CrossRefGoogle Scholar
Glasner, E. and Glasner, Y.. A metric minimal PI cascade with
${2}^{\mathfrak{c}}$
minimal ideals. Ergod. Th. & Dynam. Sys. 40(5) (2020), 1268–1281.CrossRefGoogle Scholar
${2}^{\mathfrak{c}}$
minimal ideals. Ergod. Th. & Dynam. Sys. 40(5) (2020), 1268–1281.CrossRefGoogle ScholarGlasner, E. and Megrelishvili, M.. Hereditarily non-sensitive dynamical systems and linear representations. Colloq. Math. 104 (2006), 223–283.CrossRefGoogle Scholar
Hindman, N. and Strauss, D.. Algebra in the Stone–Cech Compactification: Theory and Applications. Walter de Gruyter, Berlin, 2011.CrossRefGoogle Scholar
Howie, J. M.. Fundamentals of Semigroup Theory (London Mathematical Society Monographs, New Series, 12). Clarendon, Oxford, 1995.CrossRefGoogle Scholar
Kellendonk, J. and Yassawi, R.. The Ellis semigroup of bijective substitutions. Groups Geom. Dyn. 16(1) (2022), 29–73.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Independence in topological and
${\mathrm{C}}^{\ast }$
-dynamics. Math. Ann. 338(4) (2007), 869–926.CrossRefGoogle Scholar
${\mathrm{C}}^{\ast }$
-dynamics. Math. Ann. 338(4) (2007), 869–926.CrossRefGoogle ScholarKöhler, A.. Enveloping semigroups for flows. Proc. R. Ir. Acad. Sect. A 95(2) (1995), 179–191.Google Scholar
Sacker, R. J. and Sell, G. R.. Finite extensions of minimal transformation groups. Trans. Amer. Math. Soc. 190 (1974), 325–334.CrossRefGoogle Scholar