Article contents
On nilspace systems and their morphisms
Published online by Cambridge University Press: 10 April 2019
Abstract
A nilspace system is a generalization of a nilsystem, consisting of a compact nilspace 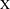 $\text{X}$ equipped with a group of nilspace translations acting on
$\text{X}$ equipped with a group of nilspace translations acting on 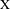 $\text{X}$ . Nilspace systems appear in different guises in several recent works and this motivates the study of these systems per se as well as their relation to more classical types of systems. In this paper we study morphisms of nilspace systems, i.e., nilspace morphisms with the additional property of being consistent with the actions of the given translations. A nilspace morphism does not necessarily have this property, but one of our main results shows that it factors through some other morphism which does have the property. As an application we obtain a strengthening of the inverse limit theorem for compact nilspaces, valid for nilspace systems. This is used in work of the first- and third-named authors to generalize the celebrated structure theorem of Host and Kra on characteristic factors.
$\text{X}$ . Nilspace systems appear in different guises in several recent works and this motivates the study of these systems per se as well as their relation to more classical types of systems. In this paper we study morphisms of nilspace systems, i.e., nilspace morphisms with the additional property of being consistent with the actions of the given translations. A nilspace morphism does not necessarily have this property, but one of our main results shows that it factors through some other morphism which does have the property. As an application we obtain a strengthening of the inverse limit theorem for compact nilspaces, valid for nilspace systems. This is used in work of the first- and third-named authors to generalize the celebrated structure theorem of Host and Kra on characteristic factors.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 8
- Cited by


