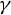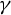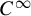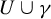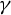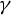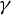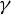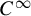1 Introduction and main results
The billiard reflection from a strictly convex smooth planar curve
![]() $\gamma \subset {\mathbb R}^2$
(parameterized by either a circle or an interval) is a map
$\gamma \subset {\mathbb R}^2$
(parameterized by either a circle or an interval) is a map
![]() ${\mathcal T}$
acting on the subset in the space of oriented lines that consists of those lines that are either tangent to
${\mathcal T}$
acting on the subset in the space of oriented lines that consists of those lines that are either tangent to
![]() $\gamma $
or intersect
$\gamma $
or intersect
![]() $\gamma $
transversally at two points. (In general, the latter subset is not
$\gamma $
transversally at two points. (In general, the latter subset is not
![]() ${\mathcal T}$
-invariant. In the case when
${\mathcal T}$
-invariant. In the case when
![]() $\gamma $
is a closed curve, the latter subset is
$\gamma $
is a closed curve, the latter subset is
![]() ${\mathcal T}$
-invariant and called the phase cylinder.) Namely, if a line is tangent to
${\mathcal T}$
-invariant and called the phase cylinder.) Namely, if a line is tangent to
![]() $\gamma $
, then it is a fixed point of the reflection map. If a line L intersects
$\gamma $
, then it is a fixed point of the reflection map. If a line L intersects
![]() $\gamma $
transversally at two points, take its last intersection point B with
$\gamma $
transversally at two points, take its last intersection point B with
![]() $\gamma $
(in the sense of orientation of the line L) and reflect L from
$\gamma $
(in the sense of orientation of the line L) and reflect L from
![]() $T_B\gamma $
according to the usual reflection law: the angle of incidence is equal to the angle of reflection. By definition, the image
$T_B\gamma $
according to the usual reflection law: the angle of incidence is equal to the angle of reflection. By definition, the image
![]() ${\mathcal T}(L)$
is the reflected line oriented at B inside the convex domain adjacent to
${\mathcal T}(L)$
is the reflected line oriented at B inside the convex domain adjacent to
![]() $\gamma $
. The reflection map
$\gamma $
. The reflection map
![]() ${\mathcal T}$
is called the billiard ball map. See Figure 1.
${\mathcal T}$
is called the billiard ball map. See Figure 1.
The space of oriented lines in Euclidean plane
![]() ${\mathbb R}^2_{x,y}$
is homeomorphic to a cylinder, and it carries the standard symplectic form
${\mathbb R}^2_{x,y}$
is homeomorphic to a cylinder, and it carries the standard symplectic form
where
![]() $\phi =\phi (L)$
is the azimuth of the line L (its angle with the x-axis) and
$\phi =\phi (L)$
is the azimuth of the line L (its angle with the x-axis) and
![]() $p=p(L)$
is its signed distance to the origin O defined as follows. For each oriented line L that does not pass through O, consider the circle centered at O and tangent to L. We say that L is clockwise (counterclockwise), if it orients the latter circle clockwise (counterclockwise). By definition:
$p=p(L)$
is its signed distance to the origin O defined as follows. For each oriented line L that does not pass through O, consider the circle centered at O and tangent to L. We say that L is clockwise (counterclockwise), if it orients the latter circle clockwise (counterclockwise). By definition:
-
•
 $p(L)=0$
if and only if L passes through the origin O;
$p(L)=0$
if and only if L passes through the origin O; -
•
 $p={\operatorname {dist}}(L,O)$
if L is clockwise; otherwise
$p={\operatorname {dist}}(L,O)$
if L is clockwise; otherwise
 $p=-{\operatorname {dist}}(L,O)$
.
$p=-{\operatorname {dist}}(L,O)$
.
Figure 1 The billiard ball map and a caustic.
It is well known that:
-
• the symplectic form
 $\omega $
is invariant under affine orientation-preserving isometries;
$\omega $
is invariant under affine orientation-preserving isometries; -
• the billiard reflections from all planar curves preserve the symplectic form
 $\omega $
.
$\omega $
.
Definition 1.1. A curve C is a caustic for the billiard on the curve
![]() $\gamma $
if each line tangent to C is reflected from
$\gamma $
if each line tangent to C is reflected from
![]() $\gamma $
to a line tangent to C. See Figure 1. Here the tangent line is taken with arbitrary orientation, for which its reflection is well defined: the notion of caustic is orientation independent.
$\gamma $
to a line tangent to C. See Figure 1. Here the tangent line is taken with arbitrary orientation, for which its reflection is well defined: the notion of caustic is orientation independent.
Remark 1.2. Consider the union
![]() ${\mathcal U}_C$
of two families of oriented tangent lines to a curve C: lines taken with two possible orientations. The curve C is a caustic if and only if the intersection of the set
${\mathcal U}_C$
of two families of oriented tangent lines to a curve C: lines taken with two possible orientations. The curve C is a caustic if and only if the intersection of the set
![]() ${\mathcal U}_C$
with the definition domain of the billiard ball map is sent by the billiard map to
${\mathcal U}_C$
with the definition domain of the billiard ball map is sent by the billiard map to
![]() $\mathcal U_C$
. Note that a single family of tangent lines to a caustic need not be invariant. For example, in an elliptic billiard, each confocal hyperbola is a caustic, but its two families of tangent lines are permuted by the billiard map. However, each confocal ellipse is a caustic, with both tangent line families being invariant curves. If a caustic of a general strictly convex billiard is
$\mathcal U_C$
. Note that a single family of tangent lines to a caustic need not be invariant. For example, in an elliptic billiard, each confocal hyperbola is a caustic, but its two families of tangent lines are permuted by the billiard map. However, each confocal ellipse is a caustic, with both tangent line families being invariant curves. If a caustic of a general strictly convex billiard is
![]() $C^1$
-close enough to the billiard boundary, then each individual family of its tangent lines is an invariant curve for the billiard map. For more details, see Remark 1.4.
$C^1$
-close enough to the billiard boundary, then each individual family of its tangent lines is an invariant curve for the billiard map. For more details, see Remark 1.4.
The famous Birkhoff conjecture deals with a planar billiard bounded by a strictly convex closed curve
![]() $\gamma $
. Recall that such a billiard is called Birkhoff integrable if there exists a topological annulus adjacent to
$\gamma $
. Recall that such a billiard is called Birkhoff integrable if there exists a topological annulus adjacent to
![]() $\gamma $
from the convex side foliated by closed caustics, and
$\gamma $
from the convex side foliated by closed caustics, and
![]() $\gamma $
is a leaf of this foliation. See Figure 2. It is well known that the billiard in an ellipse is integrable, since it has a family of closed caustics: confocal ellipses. The Birkhoff conjecture states the converse: the only integrable planar billiards are ellipses.
$\gamma $
is a leaf of this foliation. See Figure 2. It is well known that the billiard in an ellipse is integrable, since it has a family of closed caustics: confocal ellipses. The Birkhoff conjecture states the converse: the only integrable planar billiards are ellipses.

Figure 2 A Birkhoff integrable billiard.
Remark 1.3. The condition of the Birkhoff conjecture stating that the caustics in question form a foliation is important: the famous result by Lazutkin [Reference Lazutkin15] (1973) states that each strictly convex bounded planar billiard with boundary smooth enough has a Cantor family of closed caustics. Lazutkin proved it by using Kolmogorov–Arnold–Moser-type arguments. However, Lazutkin’s caustic family does not extend to a foliation in general.
The main result of the paper presented in §1.2 shows that the other condition of the Birkhoff conjecture stating that the caustics in question are closed is also important: the Birkhoff conjecture is false without closeness condition. Namely, we show that any open strictly convex
![]() $C^\infty $
-smooth planar curve
$C^\infty $
-smooth planar curve
![]() $\gamma $
has an adjacent domain U (from the convex side) admitting a foliation by caustics of
$\gamma $
has an adjacent domain U (from the convex side) admitting a foliation by caustics of
![]() $\gamma $
that extends to a
$\gamma $
that extends to a
![]() $C^\infty $
-smooth foliation of the domain with boundary
$C^\infty $
-smooth foliation of the domain with boundary
![]() $U\cup \gamma $
with
$U\cup \gamma $
with
![]() $\gamma $
being a leaf. (The exact sense of the notion ‘foliation by caustics’ for a strictly convex open billiard will be given in Definition 1.6 and Remark 1.7.) Moreover, we show that U can be chosen so that there exist infinitely many (continuum of) such foliations, and any two distinct foliations have pairwise distinct germs at every point in
$\gamma $
being a leaf. (The exact sense of the notion ‘foliation by caustics’ for a strictly convex open billiard will be given in Definition 1.6 and Remark 1.7.) Moreover, we show that U can be chosen so that there exist infinitely many (continuum of) such foliations, and any two distinct foliations have pairwise distinct germs at every point in
![]() $\gamma $
. We prove an analogous statement for a non-injectively immersed curve
$\gamma $
. We prove an analogous statement for a non-injectively immersed curve
![]() $\gamma $
and ‘immersed foliations’ by immersed caustics. We state and prove an analogue of this statement in the special case, when
$\gamma $
and ‘immersed foliations’ by immersed caustics. We state and prove an analogue of this statement in the special case, when
![]() $\gamma $
is a closed curve.
$\gamma $
is a closed curve.
The above-mentioned results extend a previous result of Melrose, who proved that for every
![]() $C^\infty $
-smooth germ
$C^\infty $
-smooth germ
![]() $\gamma $
of a strictly convex planar curve, there exists a germ of
$\gamma $
of a strictly convex planar curve, there exists a germ of
![]() $C^\infty $
-smooth foliation by caustics of the billiard played on
$C^\infty $
-smooth foliation by caustics of the billiard played on
![]() $\gamma $
, with
$\gamma $
, with
![]() $\gamma $
being a leaf [Reference Melrose17, p. 184, Proposition 7.14].
$\gamma $
being a leaf [Reference Melrose17, p. 184, Proposition 7.14].
Remark 1.4. Consider the map
![]() ${\mathcal T}$
of billiard reflections from a strictly convex planar oriented
${\mathcal T}$
of billiard reflections from a strictly convex planar oriented
![]() $C^{\infty }$
-smooth curve
$C^{\infty }$
-smooth curve
![]() $\gamma $
that is a one-dimensional submanifold in
$\gamma $
that is a one-dimensional submanifold in
![]() ${\mathbb R}^2$
parameterized by interval. Let
${\mathbb R}^2$
parameterized by interval. Let
![]() $\widehat {\gamma }$
denote the family of its orienting tangent lines. Then the points of the curve
$\widehat {\gamma }$
denote the family of its orienting tangent lines. Then the points of the curve
![]() $\widehat {\gamma }$
are fixed by
$\widehat {\gamma }$
are fixed by
![]() ${\mathcal T}$
. The map
${\mathcal T}$
. The map
![]() ${\mathcal T}$
is a well-defined area-preserving map on an open subset adjacent to
${\mathcal T}$
is a well-defined area-preserving map on an open subset adjacent to
![]() $\widehat {\gamma }$
in the space of oriented lines. The latter subset consists of those lines that intersect
$\widehat {\gamma }$
in the space of oriented lines. The latter subset consists of those lines that intersect
![]() $\gamma $
transversally and are directed to the concave side from
$\gamma $
transversally and are directed to the concave side from
![]() $\gamma $
at some intersection point. Each caustic close to
$\gamma $
at some intersection point. Each caustic close to
![]() $\gamma $
corresponds to a
$\gamma $
corresponds to a
![]() ${\mathcal T}$
-invariant curve (the family of its tangent lines chosen with appropriate orientation) and vice versa. Thus, a foliation by caustics induces a foliation by
${\mathcal T}$
-invariant curve (the family of its tangent lines chosen with appropriate orientation) and vice versa. Thus, a foliation by caustics induces a foliation by
![]() ${\mathcal T}$
-invariant curves. In §2.7, we prove the converse: each
${\mathcal T}$
-invariant curves. In §2.7, we prove the converse: each
![]() $C^{\infty }$
-smooth foliation by
$C^{\infty }$
-smooth foliation by
![]() ${\mathcal T}$
-invariant curves on a domain adjacent to
${\mathcal T}$
-invariant curves on a domain adjacent to
![]() $\widehat {\gamma }$
from an appropriate side (with
$\widehat {\gamma }$
from an appropriate side (with
![]() $\widehat {\gamma }$
being a leaf) induces a
$\widehat {\gamma }$
being a leaf) induces a
![]() $C^{\infty }$
-smooth foliation by caustics (with
$C^{\infty }$
-smooth foliation by caustics (with
![]() $\gamma $
being a leaf).
$\gamma $
being a leaf).
We show that the billiard map has an infinite-dimensional family of
![]() $C^{\infty }$
-smooth foliations by invariant curves (including
$C^{\infty }$
-smooth foliations by invariant curves (including
![]() $\widehat {\gamma }$
) in an appropriate domain adjacent to
$\widehat {\gamma }$
) in an appropriate domain adjacent to
![]() $\widehat {\gamma }$
with pairwise distinct germs at each point of the curve
$\widehat {\gamma }$
with pairwise distinct germs at each point of the curve
![]() $\widehat {\gamma }$
. This together with Remark 1.4 implies the existence of an infinite-dimensional family of foliations by caustics.
$\widehat {\gamma }$
. This together with Remark 1.4 implies the existence of an infinite-dimensional family of foliations by caustics.
In §1.4, we state the generalization of the above result on foliations by invariant curves to a special class of area-preserving maps: the so-called
![]() $C^{\infty }$
-lifted strongly billiard-like maps. Each one of the latter maps is defined on a domain
$C^{\infty }$
-lifted strongly billiard-like maps. Each one of the latter maps is defined on a domain
![]() $U\subset {\mathbb R}\times {\mathbb R}_{>0}$
taken together with an adjacent boundary interval
$U\subset {\mathbb R}\times {\mathbb R}_{>0}$
taken together with an adjacent boundary interval
![]() $J\subset {\mathbb R}\times \{0\}$
consisting of fixed points, and satisfies appropriate twist and regularity conditions. The (weakly and strongly) billiard-like maps were introduced and studied in [Reference Glutsyuk10], where results on their dynamics were applied to curves with Poritsky property. For the
$J\subset {\mathbb R}\times \{0\}$
consisting of fixed points, and satisfies appropriate twist and regularity conditions. The (weakly and strongly) billiard-like maps were introduced and studied in [Reference Glutsyuk10], where results on their dynamics were applied to curves with Poritsky property. For the
![]() $C^{\infty }$
-lifted strongly billiard-like maps, we prove the existence of an infinite-dimensional family of
$C^{\infty }$
-lifted strongly billiard-like maps, we prove the existence of an infinite-dimensional family of
![]() $C^{\infty }$
-smooth foliations by invariant curves with pairwise distinct germs at each point of the boundary segment. In §1.5, we describe one-to-one correspondence between germs of the latter foliations and germs at
$C^{\infty }$
-smooth foliations by invariant curves with pairwise distinct germs at each point of the boundary segment. In §1.5, we describe one-to-one correspondence between germs of the latter foliations and germs at
![]() $S^1\times \{0\}$
of
$S^1\times \{0\}$
of
![]() $C^{\infty }$
-smooth h-flat functions
$C^{\infty }$
-smooth h-flat functions
![]() $\psi (t,h)$
on the cylinder
$\psi (t,h)$
on the cylinder
![]() $S^1\times {\mathbb R}_{\geq 0}$
such that
$S^1\times {\mathbb R}_{\geq 0}$
such that
![]() $\psi (0,h)\equiv 0$
. This yields a one-to-one correspondence between foliations by caustics and the above germs of flat functions on a cylinder. Theorem 1.31 stated in §1.5 asserts that all the foliations by caustics (invariant curves) corresponding to a given billiard (map) have coinciding jets of any order at each point of the boundary curve.
$\psi (0,h)\equiv 0$
. This yields a one-to-one correspondence between foliations by caustics and the above germs of flat functions on a cylinder. Theorem 1.31 stated in §1.5 asserts that all the foliations by caustics (invariant curves) corresponding to a given billiard (map) have coinciding jets of any order at each point of the boundary curve.
The results of the paper mentioned below are motivated by the following open question attributed to Victor Guillemin:
Let two billiard maps corresponding to two strictly convex closed Jordan curves be conjugated by a homeomorphism. What can be said about the curves? Are they similar (that is, of the same shape)?
Theorem 1.27 presented in §1.4 states that each
![]() $C^{\infty }$
-lifted strongly billiard-like map is
$C^{\infty }$
-lifted strongly billiard-like map is
![]() $C^\infty $
-smoothly symplectically conjugated near the boundary (and up to the boundary) to the normal form
$C^\infty $
-smoothly symplectically conjugated near the boundary (and up to the boundary) to the normal form
![]() $(t,z)\mapsto (t+\sqrt z,z)$
restricted to
$(t,z)\mapsto (t+\sqrt z,z)$
restricted to
![]() $U\cup J$
, where
$U\cup J$
, where
![]() $J\subset {\mathbb R}\times \{0\}$
is an interval of the horizontal axis and
$J\subset {\mathbb R}\times \{0\}$
is an interval of the horizontal axis and
![]() $U\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J. In particular, this holds for the billiard map corresponding to each
$U\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J. In particular, this holds for the billiard map corresponding to each
![]() $C^\infty $
-smooth strictly convex (immersed) curve. As an application, we obtain a series of results on (symplectic) conjugacy of billiard maps near the boundary for billiards with reflections from
$C^\infty $
-smooth strictly convex (immersed) curve. As an application, we obtain a series of results on (symplectic) conjugacy of billiard maps near the boundary for billiards with reflections from
![]() $C^\infty $
-smooth strictly convex curves parameterized by intervals. These conjugacy results are stated in §1.6 and proved in §2.10. One of them (Theorem 1.39) states that for any two strictly convex open billiards, each of them being bounded by an infinite curve with asymptotic tangent line at infinity in each direction, the corresponding billiard maps are
$C^\infty $
-smooth strictly convex curves parameterized by intervals. These conjugacy results are stated in §1.6 and proved in §2.10. One of them (Theorem 1.39) states that for any two strictly convex open billiards, each of them being bounded by an infinite curve with asymptotic tangent line at infinity in each direction, the corresponding billiard maps are
![]() $C^\infty $
-smoothly conjugated near the boundary.
$C^\infty $
-smoothly conjugated near the boundary.
The results of the paper are proved in §2. The plan of proofs is presented in §1.7. The corresponding background material on symplectic properties of a billiard ball map is recalled in §1.3.
1.1 Historical remarks
The Birkhoff conjecture was first stated in print by Poritsky [Reference Poritsky19], who proved it under an additional condition that for any two nested closed caustics, the smaller one is a caustic of the billiard played in the bigger one; the same result was later obtained in [Reference Amiran1]. One of the most famous results on the Birkhoff conjecture is due to Bialy [Reference Bialy4], who proved that if the phase cylinder of the billiard is foliated by non-contractible invariant closed curves, then the billiard boundary is a circle; see also another proof in [Reference Wojtkowski22]. Recently, Kaloshin and Sorrentino proved that any integrable deformation of an ellipse is an ellipse [Reference Kaloshin and Sorrentino13]. Very recently, Bialy and Mironov proved the Birkhoff conjecture for centrally symmetric billiards having a family of closed caustics that extends up to a caustic tangent to four-periodic orbits [Reference Bialy and Mironov7]. For a detailed survey of the Birkhoff conjecture, see [Reference Bialy and Mironov5, Reference Bialy and Mironov7–Reference Glutsyuk9, Reference Kaloshin and Sorrentino13, Reference Kaloshin and Sorrentino14, Reference Tabachnikov21] and references therein.
Marvizi and Melrose have shown that the billiard ball map
![]() ${\mathcal T}$
in a planar domain bounded by a
${\mathcal T}$
in a planar domain bounded by a
![]() $C^\infty $
-smooth strictly convex closed curve
$C^\infty $
-smooth strictly convex closed curve
![]() $\gamma $
always has an asymptotic first integral on a domain with boundary in the space of oriented lines: a domain adjacent to the family of tangent lines to
$\gamma $
always has an asymptotic first integral on a domain with boundary in the space of oriented lines: a domain adjacent to the family of tangent lines to
![]() $\gamma $
. Namely, there exists a
$\gamma $
. Namely, there exists a
![]() $C^\infty $
-smooth function F on the closure of a domain as above such that the difference
$C^\infty $
-smooth function F on the closure of a domain as above such that the difference
![]() $F\circ {\mathcal T}-F$
is
$F\circ {\mathcal T}-F$
is
![]() $C^\infty $
-smooth there, and it is flat at the points of the family of tangent lines to
$C^\infty $
-smooth there, and it is flat at the points of the family of tangent lines to
![]() $\gamma $
; see [Reference Marvizi and Melrose16, Theorem 3.2]; see also the statement of their result in Theorem 2.1.
$\gamma $
; see [Reference Marvizi and Melrose16, Theorem 3.2]; see also the statement of their result in Theorem 2.1.
Kaloshin and Koudjinan proved that for a non-integrable billiard bounded by a strictly convex closed curve, the Taylor coefficients of the normalized Mather
![]() $\beta $
-function are invariant under
$\beta $
-function are invariant under
![]() $C^\infty $
-conjugacies [Reference Kaloshin and Koudjinan12]. They also obtained a series of results on conjugacy of elliptic billiard maps, showing in particular that global topological conjugacy implies similarity of underlying ellipses.
$C^\infty $
-conjugacies [Reference Kaloshin and Koudjinan12]. They also obtained a series of results on conjugacy of elliptic billiard maps, showing in particular that global topological conjugacy implies similarity of underlying ellipses.
1.2 Main result: an open convex arc has infinitely many foliations by caustics
Consider an open planar billiard: a convex planar domain bounded by a strictly convex
![]() $C^\infty $
-smooth one-dimensional submanifold
$C^\infty $
-smooth one-dimensional submanifold
![]() $\gamma $
that is a curve parameterized by interval; it goes to infinity in both directions. Let U be a domain adjacent to
$\gamma $
that is a curve parameterized by interval; it goes to infinity in both directions. Let U be a domain adjacent to
![]() $\gamma $
from the convex side. Consider a foliation
$\gamma $
from the convex side. Consider a foliation
![]() ${\mathcal F}$
of the domain U by strictly convex smooth curves, with
${\mathcal F}$
of the domain U by strictly convex smooth curves, with
![]() $\gamma $
being a leaf. We consider that it is a foliation by (connected components of) level curves of a continuous function h on
$\gamma $
being a leaf. We consider that it is a foliation by (connected components of) level curves of a continuous function h on
![]() $U\cup \gamma $
such that
$U\cup \gamma $
such that
![]() $h|_\gamma =0$
,
$h|_\gamma =0$
,
![]() $h|_U>0$
and h strictly increases as a function of the transversal parameter. We also consider that for every
$h|_U>0$
and h strictly increases as a function of the transversal parameter. We also consider that for every
![]() $x\in \gamma $
and every leaf
$x\in \gamma $
and every leaf
![]() ${\mathcal L}$
of the foliation
${\mathcal L}$
of the foliation
![]() ${\mathcal F}$
, there are at most two tangent lines to
${\mathcal F}$
, there are at most two tangent lines to
![]() ${\mathcal L}$
through x. One can achieve this by shrinking the foliated domain U, since for every
${\mathcal L}$
through x. One can achieve this by shrinking the foliated domain U, since for every
![]() $x\in \gamma $
, the line
$x\in \gamma $
, the line
![]() $T_x\gamma $
is the only line through x tangent to
$T_x\gamma $
is the only line through x tangent to
![]() $\gamma $
. Indeed, if there were another line through x tangent to
$\gamma $
. Indeed, if there were another line through x tangent to
![]() $\gamma $
at a point
$\gamma $
at a point
![]() $y\neq x$
, then the total increment of azimuth of the orienting tangent vector to
$y\neq x$
, then the total increment of azimuth of the orienting tangent vector to
![]() $\gamma $
along the arc
$\gamma $
along the arc
![]() $xy$
would be greater than
$xy$
would be greater than
![]() $\pi $
. However, the latter azimuth is monotonous, and its total increment along the curve
$\pi $
. However, the latter azimuth is monotonous, and its total increment along the curve
![]() $\gamma $
is no greater than
$\gamma $
is no greater than
![]() $\pi $
, since
$\pi $
, since
![]() $\gamma $
is convex and goes to infinity in both directions. The contradiction thus obtained proves uniqueness of tangent line through x.
$\gamma $
is convex and goes to infinity in both directions. The contradiction thus obtained proves uniqueness of tangent line through x.
Remark 1.5. In the above conditions, for every compact subarc
![]() $\gamma '\subset \gamma $
and every leaf
$\gamma '\subset \gamma $
and every leaf
![]() ${\mathcal L}$
of the foliation
${\mathcal L}$
of the foliation
![]() ${\mathcal F}$
close enough to
${\mathcal F}$
close enough to
![]() $\gamma $
for every
$\gamma $
for every
![]() $x\in \gamma '$
, there exist exactly two tangent lines to
$x\in \gamma '$
, there exist exactly two tangent lines to
![]() ${\mathcal L}$
through x. This follows from convexity.
${\mathcal L}$
through x. This follows from convexity.
Definition 1.6. We say that
![]() ${\mathcal F}$
is a foliation by caustics of the billiard played on
${\mathcal F}$
is a foliation by caustics of the billiard played on
![]() $\gamma $
if its leaves are caustics, see Figure 3, in the following sense. Let
$\gamma $
if its leaves are caustics, see Figure 3, in the following sense. Let
![]() $x\in \gamma $
, and let
$x\in \gamma $
, and let
![]() ${\mathcal L}$
be a leaf of the foliation
${\mathcal L}$
be a leaf of the foliation
![]() ${\mathcal F}$
. If there exist two tangent lines to
${\mathcal F}$
. If there exist two tangent lines to
![]() ${\mathcal L}$
through x, then they are symmetric with respect to the tangent line
${\mathcal L}$
through x, then they are symmetric with respect to the tangent line
![]() $T_x\gamma $
.
$T_x\gamma $
.

Figure 3 Foliation by caustics in an open strictly convex planar billiard. Here the ambient plane
![]() ${\mathbb R}^2$
is presented together with its boundary: the infinity line.
${\mathbb R}^2$
is presented together with its boundary: the infinity line.
Remark 1.7. The above definition also makes sense in the case when
![]() $\gamma $
is just a strictly convex arc that needs not go to infinity. A priori, in this case for some
$\gamma $
is just a strictly convex arc that needs not go to infinity. A priori, in this case for some
![]() $x\in \gamma $
, there may be more than two tangent lines through x to a leaf of the foliation, even for leaves arbitrarily close to
$x\in \gamma $
, there may be more than two tangent lines through x to a leaf of the foliation, even for leaves arbitrarily close to
![]() $\gamma $
. This holds, e.g., if there is a line through x tangent to
$\gamma $
. This holds, e.g., if there is a line through x tangent to
![]() $\gamma $
at a point distinct from x. This may take place only in the case when the azimuth increment along
$\gamma $
at a point distinct from x. This may take place only in the case when the azimuth increment along
![]() $\gamma $
of the orienting tangent vector to
$\gamma $
of the orienting tangent vector to
![]() $\gamma $
is bigger than
$\gamma $
is bigger than
![]() $\pi $
. In this case, we modify the above definition as follows. Let
$\pi $
. In this case, we modify the above definition as follows. Let
![]() $\mathcal H$
denote the space of triples
$\mathcal H$
denote the space of triples
![]() $(x,y,z)$
, where
$(x,y,z)$
, where
![]() $x\in \gamma $
and y, z lie in the same leaf
$x\in \gamma $
and y, z lie in the same leaf
![]() ${\mathcal L}$
of the foliation
${\mathcal L}$
of the foliation
![]() ${\mathcal F}$
,
${\mathcal F}$
,
![]() $y\neq z$
, such that the lines
$y\neq z$
, such that the lines
![]() $xy$
and
$xy$
and
![]() $xz$
are tangent to
$xz$
are tangent to
![]() ${\mathcal L}$
at the points y and z respectively. Set
${\mathcal L}$
at the points y and z respectively. Set
Let
![]() ${\mathcal H}_0$
denote the path-connected component of the space
${\mathcal H}_0$
denote the path-connected component of the space
![]() $\overline {\mathcal H}$
that contains
$\overline {\mathcal H}$
that contains
![]() $\Delta $
. We require that for every
$\Delta $
. We require that for every
![]() $(x,y,z)\in {\mathcal H}_0\setminus \Delta $
, the lines
$(x,y,z)\in {\mathcal H}_0\setminus \Delta $
, the lines
![]() $xy$
and
$xy$
and
![]() $xz$
be symmetric with respect to the line
$xz$
be symmetric with respect to the line
![]() $T_x\gamma $
.
$T_x\gamma $
.
Definition 1.8. Let
![]() $\gamma \subset {\mathbb R}^2$
be a smooth curve parameterized by an interval. Let
$\gamma \subset {\mathbb R}^2$
be a smooth curve parameterized by an interval. Let
![]() $U\subset {\mathbb R}^2$
be a domain adjacent to
$U\subset {\mathbb R}^2$
be a domain adjacent to
![]() $\gamma $
. A collection of
$\gamma $
. A collection of
![]() $C^\infty $
-smooth foliations on
$C^\infty $
-smooth foliations on
![]() $U\cup \gamma $
with
$U\cup \gamma $
with
![]() $\gamma $
being a leaf is said to be an infinite-dimensional family of foliations with distinct boundary germs if their germs at each point in
$\gamma $
being a leaf is said to be an infinite-dimensional family of foliations with distinct boundary germs if their germs at each point in
![]() $\gamma $
are pairwise distinct, and if their collection contains a
$\gamma $
are pairwise distinct, and if their collection contains a
![]() $C^\infty $
-smooth N-parametric family of foliations for every
$C^\infty $
-smooth N-parametric family of foliations for every
![]() $N\in {\mathbb N}$
.
$N\in {\mathbb N}$
.
Theorem 1.9.
-
(1) Consider an open billiard bounded by a strictly convex
 $C^{\infty }$
-smooth curve
$C^{\infty }$
-smooth curve
 $\gamma \subset {\mathbb R}^2$
: a one-dimensional submanifold parameterized by interval. There exists a simply connected domain U adjacent to
$\gamma \subset {\mathbb R}^2$
: a one-dimensional submanifold parameterized by interval. There exists a simply connected domain U adjacent to
 $\gamma $
from the convex side that admits a foliation by caustics of the billiard that extends to a
$\gamma $
from the convex side that admits a foliation by caustics of the billiard that extends to a
 $C^\infty $
-smooth foliation on
$C^\infty $
-smooth foliation on
 $U\cup \gamma $
, with
$U\cup \gamma $
, with
 $\gamma $
being a leaf. Moreover, U can be chosen to admit an infinite-dimensional family of foliations as above with distinct boundary germs. See Figure 3.
$\gamma $
being a leaf. Moreover, U can be chosen to admit an infinite-dimensional family of foliations as above with distinct boundary germs. See Figure 3. -
(2) The above statements remain valid in the case when
 $\gamma $
is just an arc: a strictly convex curve parameterized by an interval such that each its point has a neighborhood V whose intersection with
$\gamma $
is just an arc: a strictly convex curve parameterized by an interval such that each its point has a neighborhood V whose intersection with
 $\gamma $
is a submanifold in V.
$\gamma $
is a submanifold in V.
Remark 1.10. It follows from Melrose’s result [Reference Melrose17, p. 184, Proposition 7.14] that each point of the curve
![]() $\gamma $
has an arc neighborhood
$\gamma $
has an arc neighborhood
![]() $\alpha \subset \gamma $
for which there exists a domain U adjacent to
$\alpha \subset \gamma $
for which there exists a domain U adjacent to
![]() $\alpha $
from the convex side such that
$\alpha $
from the convex side such that
![]() $U\cup \alpha $
is
$U\cup \alpha $
is
![]() $C^{\infty }$
-smoothly foliated by caustics of the billiard played on
$C^{\infty }$
-smoothly foliated by caustics of the billiard played on
![]() $\gamma $
. The new result given by Theorem 1.9 is the statement that the latter holds for the whole curve
$\gamma $
. The new result given by Theorem 1.9 is the statement that the latter holds for the whole curve
![]() $\gamma $
and there exist infinitely many foliations by caustics with distinct boundary germs.
$\gamma $
and there exist infinitely many foliations by caustics with distinct boundary germs.
Below we extend Theorem 1.9 to the case of immersed (or closed) curve
![]() $\gamma $
.
$\gamma $
.
Definition 1.11. Let
![]() $\gamma \subset {\mathbb R}^2$
be a strictly convex
$\gamma \subset {\mathbb R}^2$
be a strictly convex
![]() $C^{\infty }$
-smooth curve that is the image of an interval
$C^{\infty }$
-smooth curve that is the image of an interval
![]() $(0,1)$
with coordinate x under an immersion
$(0,1)$
with coordinate x under an immersion
![]() $\psi :(0,1)\to \gamma $
. Let
$\psi :(0,1)\to \gamma $
. Let
![]() $V\subset (0,1)\times {\mathbb R}_+\subset {\mathbb R}^2$
be a domain adjacent to the interval
$V\subset (0,1)\times {\mathbb R}_+\subset {\mathbb R}^2$
be a domain adjacent to the interval
![]() ${J:=(0,1)\times \{0\}}$
. Fix a
${J:=(0,1)\times \{0\}}$
. Fix a
![]() $C^{\infty }$
-smooth immersion
$C^{\infty }$
-smooth immersion
![]() $\Psi : V\cup J\to {\mathbb R}^2$
extending
$\Psi : V\cup J\to {\mathbb R}^2$
extending
![]() $\psi $
as a map
$\psi $
as a map
![]() $J\to \gamma $
, sending V to the convex side from
$J\to \gamma $
, sending V to the convex side from
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $U\subset V$
be a domain adjacent to J and equipped with a foliation
$U\subset V$
be a domain adjacent to J and equipped with a foliation
![]() ${\mathcal F}$
by smooth curves parameterized by intervals, with J being a leaf. We consider that
${\mathcal F}$
by smooth curves parameterized by intervals, with J being a leaf. We consider that
![]() ${\mathcal F}$
is a foliation by level curves of a continuous function
${\mathcal F}$
is a foliation by level curves of a continuous function
![]() $h:U\to {\mathbb R}$
,
$h:U\to {\mathbb R}$
,
![]() $h|_J=0$
,
$h|_J=0$
,
![]() $h|_U>0$
, such that h strictly increases as a function of the transversal parameter. We say that
$h|_U>0$
, such that h strictly increases as a function of the transversal parameter. We say that
![]() ${\mathcal F}$
is a foliation by lifted caustics of the billiard played on
${\mathcal F}$
is a foliation by lifted caustics of the billiard played on
![]() $\gamma $
if
$\gamma $
if
![]() $\Psi $
sends each its leaf
$\Psi $
sends each its leaf
![]() ${\mathcal F}_t=\{ h=t\}$
to a caustic of the billiard, see Figure 4. In more detail, let
${\mathcal F}_t=\{ h=t\}$
to a caustic of the billiard, see Figure 4. In more detail, let
![]() $\mathcal H$
denote the space of triples
$\mathcal H$
denote the space of triples
![]() $(x,y,z)$
, where
$(x,y,z)$
, where
![]() $x\in J$
and y, z lie in the same leaf
$x\in J$
and y, z lie in the same leaf
![]() ${\mathcal L}$
of the foliation
${\mathcal L}$
of the foliation
![]() ${\mathcal F}$
,
${\mathcal F}$
,
![]() $y\neq z$
, such that the lines
$y\neq z$
, such that the lines
![]() $\Psi (x)\Psi (y)$
and
$\Psi (x)\Psi (y)$
and
![]() $\Psi (x)\Psi (z)$
are tangent to the curve
$\Psi (x)\Psi (z)$
are tangent to the curve
![]() $\Psi ({\mathcal L})$
at the points
$\Psi ({\mathcal L})$
at the points
![]() $\Psi (y)$
and
$\Psi (y)$
and
![]() $\Psi (z)$
respectively. Set
$\Psi (z)$
respectively. Set
Let
![]() ${\mathcal H}_0$
denote the path-connected component of the space
${\mathcal H}_0$
denote the path-connected component of the space
![]() $\overline {\mathcal H}$
that contains
$\overline {\mathcal H}$
that contains
![]() $\Delta $
. We require that for every
$\Delta $
. We require that for every
![]() $(x,y,z)\in {\mathcal H}_0\setminus \Delta $
, the lines
$(x,y,z)\in {\mathcal H}_0\setminus \Delta $
, the lines
![]() $\Psi (x)\Psi (y)$
and
$\Psi (x)\Psi (y)$
and
![]() $\Psi (x)\Psi (z)$
be symmetric with respect to the line tangent to
$\Psi (x)\Psi (z)$
be symmetric with respect to the line tangent to
![]() $\gamma $
at
$\gamma $
at
![]() $\Psi (x)$
.
$\Psi (x)$
.

Figure 4 An immersed foliation by immersed caustics and a foliation by lifted caustics.
Theorem 1.12. Let
![]() $\gamma $
,
$\gamma $
,
![]() $\psi $
,
$\psi $
,
![]() $\Psi $
, J, V be as above. There exists a domain
$\Psi $
, J, V be as above. There exists a domain
![]() $U\subset V$
adjacent to J on which there exists a foliation by lifted caustics that extends to a
$U\subset V$
adjacent to J on which there exists a foliation by lifted caustics that extends to a
![]() $C^\infty $
-smooth foliation on
$C^\infty $
-smooth foliation on
![]() $U\cup J$
, with J being a leaf. The above U can be chosen so that it admits an infinite-dimensional family of foliations as above with distinct boundary germs. See Figure 4.
$U\cup J$
, with J being a leaf. The above U can be chosen so that it admits an infinite-dimensional family of foliations as above with distinct boundary germs. See Figure 4.
Theorem 1.13. Let
![]() $\gamma $
be a strictly convex closed curve bijectively parameterized by a circle. Fix a topological annulus
$\gamma $
be a strictly convex closed curve bijectively parameterized by a circle. Fix a topological annulus
![]() ${\mathcal A}$
adjacent to
${\mathcal A}$
adjacent to
![]() $\gamma $
from the convex side. Let
$\gamma $
from the convex side. Let
![]() $\pi :\widetilde {\mathcal A}={\mathbb R}\times [0,{\varepsilon } )\to {\mathcal A}$
be its universal covering, set
$\pi :\widetilde {\mathcal A}={\mathbb R}\times [0,{\varepsilon } )\to {\mathcal A}$
be its universal covering, set
![]() $J:={\mathbb R}\times \{0\}$
;
$J:={\mathbb R}\times \{0\}$
;
![]() $\pi :J\to \gamma $
is the universal covering over
$\pi :J\to \gamma $
is the universal covering over
![]() $\gamma $
. There exists a domain
$\gamma $
. There exists a domain
![]() $U\subset \widetilde {\mathcal A}\setminus J$
adjacent to J that admits a foliation by lifted caustics of the billiard in
$U\subset \widetilde {\mathcal A}\setminus J$
adjacent to J that admits a foliation by lifted caustics of the billiard in
![]() $\gamma $
that extends to a
$\gamma $
that extends to a
![]() $C^{\infty }$
-smooth foliation on
$C^{\infty }$
-smooth foliation on
![]() $U\cup J$
, with J being a leaf. Moreover, one can choose U so that there exist an infinite-dimensional family of foliations as above with distinct boundary germs.
$U\cup J$
, with J being a leaf. Moreover, one can choose U so that there exist an infinite-dimensional family of foliations as above with distinct boundary germs.
Remark 1.14. In general, in Theorem 1.13, the projected leaves are caustics that need not be closed, may intersect each other, and may have self-intersections. Each individual caustic may have a finite length. However, the latter finite length tends to infinity, as the caustic in question tends to
![]() $\gamma $
.
$\gamma $
.
Example 1.15. Let
![]() $\gamma $
be an ellipse. Then every annulus bounded by
$\gamma $
be an ellipse. Then every annulus bounded by
![]() $\gamma $
and a smaller confocal ellipse is analytically foliated by confocal elliptic caustics. The lifting of this foliation to the universal cover yields a special foliation from Theorem 1.13. Namely, its leaves are invariant under the covering action of the fundamental group of the annulus. However, a generic foliation from Theorem 1.13 need not satisfy the latter invariance statement.
$\gamma $
and a smaller confocal ellipse is analytically foliated by confocal elliptic caustics. The lifting of this foliation to the universal cover yields a special foliation from Theorem 1.13. Namely, its leaves are invariant under the covering action of the fundamental group of the annulus. However, a generic foliation from Theorem 1.13 need not satisfy the latter invariance statement.
Remark 1.16. Let
![]() $\gamma \subset {\mathbb R}^2$
be a strictly convex closed curve. Let J be its universal covering and let
$\gamma \subset {\mathbb R}^2$
be a strictly convex closed curve. Let J be its universal covering and let
![]() ${\mathcal A}$
, U, be the same, as in Theorem 1.13. Let
${\mathcal A}$
, U, be the same, as in Theorem 1.13. Let
![]() ${\mathcal F}$
be a foliation of U by lifted caustics from the same theorem and let
${\mathcal F}$
be a foliation of U by lifted caustics from the same theorem and let
![]() $b\subset U$
be its cross-section: a curve starting at a point
$b\subset U$
be its cross-section: a curve starting at a point
![]() $B\in J$
and transversal to
$B\in J$
and transversal to
![]() ${\mathcal F}$
. Let
${\mathcal F}$
. Let
![]() $b'$
,
$b'$
,
![]() $B'$
denote their images under the covering transformation defined by the generator of the fundamental group
$B'$
denote their images under the covering transformation defined by the generator of the fundamental group
![]() $\pi _1({\mathcal A})$
: the generator given by a counterclockwise circuit. The curve
$\pi _1({\mathcal A})$
: the generator given by a counterclockwise circuit. The curve
![]() $b'$
starts at
$b'$
starts at
![]() $B'$
. Both b and
$B'$
. Both b and
![]() $b'$
are projected to the same curve
$b'$
are projected to the same curve
![]() $\widehat {b}:=\pi (b)\subset {\mathcal A}\cup \gamma $
starting at
$\widehat {b}:=\pi (b)\subset {\mathcal A}\cup \gamma $
starting at
![]() $\widehat {B}:=\pi (B)=\pi (B')\in \gamma $
. The foliation
$\widehat {B}:=\pi (B)=\pi (B')\in \gamma $
. The foliation
![]() ${\mathcal F}$
induces a germ of
${\mathcal F}$
induces a germ of
![]() $C^\infty $
-smooth holonomy diffeomorphism
$C^\infty $
-smooth holonomy diffeomorphism
![]() $(b,B)\to (b',B')$
sending a point of intersection of a leaf with b to its next intersection point with
$(b,B)\to (b',B')$
sending a point of intersection of a leaf with b to its next intersection point with
![]() $b'$
: next in the sense of orientation of the leaf J given by counterclockwise orientation of the curve
$b'$
: next in the sense of orientation of the leaf J given by counterclockwise orientation of the curve
![]() $\gamma $
. This together with the identification
$\gamma $
. This together with the identification
![]() $b=b'=\widehat {b}$
yields a germ of holonomy map
$b=b'=\widehat {b}$
yields a germ of holonomy map
![]() $g: (\widehat {b},\widehat {B})\to (\widehat {b},\widehat {B})$
. In general, the germ g depends on the choice of lifting b of the curve
$g: (\widehat {b},\widehat {B})\to (\widehat {b},\widehat {B})$
. In general, the germ g depends on the choice of lifting b of the curve
![]() $\widehat {b}$
, and so does its conjugacy class. A necessary condition of Birkhoff integrability of the billiard in
$\widehat {b}$
, and so does its conjugacy class. A necessary condition of Birkhoff integrability of the billiard in
![]() $\gamma $
with foliation by closed caustics being
$\gamma $
with foliation by closed caustics being
![]() $C^\infty $
-smooth up to the boundary is the existence of a foliation
$C^\infty $
-smooth up to the boundary is the existence of a foliation
![]() ${\mathcal F}$
from Theorem 1.13 and a cross-section b for which the above germ g is the identity.
${\mathcal F}$
from Theorem 1.13 and a cross-section b for which the above germ g is the identity.
A generalization of Theorems 1.9 and 1.12 for the so-called
![]() $C^{\infty }$
-lifted strongly billiard-like maps will be stated in §1.4.
$C^{\infty }$
-lifted strongly billiard-like maps will be stated in §1.4.
1.3 Background material: symplectic properties of billiard ball map
Let
![]() $\gamma $
be a
$\gamma $
be a
![]() $C^{\infty }$
-smooth strictly convex oriented curve in
$C^{\infty }$
-smooth strictly convex oriented curve in
![]() ${\mathbb R}^2$
parameterized injectively either by an interval or by a circle. Let s be its natural length parameter respecting its orientation. We identify a point in
${\mathbb R}^2$
parameterized injectively either by an interval or by a circle. Let s be its natural length parameter respecting its orientation. We identify a point in
![]() $\gamma $
with the corresponding value of the natural parameter s. Set
$\gamma $
with the corresponding value of the natural parameter s. Set
This is a two-dimensional surface parameterized diffeomorphically by
![]() $(s,\phi )\in \gamma \times S^1$
; here
$(s,\phi )\in \gamma \times S^1$
; here
![]() $\phi =\phi (u)$
is the angle of a given unit tangent vector
$\phi =\phi (u)$
is the angle of a given unit tangent vector
![]() $u\in T_s{\mathbb R}^2$
with the orienting unit tangent vector
$u\in T_s{\mathbb R}^2$
with the orienting unit tangent vector
![]() $\dot \gamma (s)$
to
$\dot \gamma (s)$
to
![]() $\gamma $
. The curve
$\gamma $
. The curve
is the graph of the above vector field
![]() $\dot \gamma $
. For every
$\dot \gamma $
. For every
![]() $(q,u)\in \Gamma $
, set
$(q,u)\in \Gamma $
, set
We treat the two following cases separately.
Case (1). The curve
![]() $\gamma $
is either:
$\gamma $
is either:
-
• parameterized by an interval and goes to infinity in both directions (for a convex curve, this means either the existence of asymptotic rays in both directions, or converging (in both directions) to one and the same point in the infinity line in the ambient projective plane
 ${\mathbb {RP}}^2$
); or
${\mathbb {RP}}^2$
); or -
• parameterized by a circle.
That is,
![]() $\gamma $
bounds a strictly convex unbounded (respectively, bounded) planar domain. Let
$\gamma $
bounds a strictly convex unbounded (respectively, bounded) planar domain. Let
![]() $\Gamma ^0\subset \Gamma $
denote the neighborhood of the curve
$\Gamma ^0\subset \Gamma $
denote the neighborhood of the curve
![]() $\widetilde {\gamma }$
that consists of those
$\widetilde {\gamma }$
that consists of those
![]() $(q,u)\in \Gamma $
that satisfy the following conditions:
$(q,u)\in \Gamma $
that satisfy the following conditions:
-
(a) the line
 $L(q,u)$
either intersects
$L(q,u)$
either intersects
 $\gamma $
at two points q and
$\gamma $
at two points q and
 $q'$
, or is the orienting tangent line to
$q'$
, or is the orienting tangent line to
 $\gamma $
at q:
$\gamma $
at q:
 $u=\dot \gamma (s)$
; in the latter case, we set
$u=\dot \gamma (s)$
; in the latter case, we set
 $q':=q$
;
$q':=q$
; -
(b) the angle between the oriented line
 $L(q,u)$
and any of the orienting tangent vectors to
$L(q,u)$
and any of the orienting tangent vectors to
 $\gamma $
at q or
$\gamma $
at q or
 $q'$
is acute. (In the case under consideration, this condition implies that the line
$q'$
is acute. (In the case under consideration, this condition implies that the line
 $L(q,u)$
has acute angle with the orienting tangent vector
$L(q,u)$
has acute angle with the orienting tangent vector
 $\dot \gamma $
at each point of the arc
$\dot \gamma $
at each point of the arc
 $qq'$
(for appropriately chosen arc
$qq'$
(for appropriately chosen arc
 $qq'$
in the case, when
$qq'$
in the case, when
 $\gamma $
is a closed curve).)
$\gamma $
is a closed curve).)
Let
![]() $u'$
denote the directing unit vector of the line
$u'$
denote the directing unit vector of the line
![]() $L(q,u)$
at
$L(q,u)$
at
![]() $q'$
. Consider the two following involutions acting on
$q'$
. Consider the two following involutions acting on
![]() $\Gamma ^0$
and
$\Gamma ^0$
and
![]() $\Gamma $
respectively:
$\Gamma $
respectively:
 $$ \begin{align*} \beta:\Gamma^0 \to\Gamma^0,\quad \beta(q,u)=(q',u');\quad \beta^2=\mathrm{Id}; \qquad\\I:\Gamma \to\Gamma \text{ is the reflection from } T_q\gamma : I(q,u)=(q,u^*), \end{align*} $$
$$ \begin{align*} \beta:\Gamma^0 \to\Gamma^0,\quad \beta(q,u)=(q',u');\quad \beta^2=\mathrm{Id}; \qquad\\I:\Gamma \to\Gamma \text{ is the reflection from } T_q\gamma : I(q,u)=(q,u^*), \end{align*} $$
where
![]() $u^*$
is the vector symmetric to u with respect to the tangent line
$u^*$
is the vector symmetric to u with respect to the tangent line
![]() $T_q\gamma $
. Let
$T_q\gamma $
. Let
![]() $\Gamma ^0_+\subset \Gamma ^0$
denote the open subset of those pairs
$\Gamma ^0_+\subset \Gamma ^0$
denote the open subset of those pairs
![]() $(q,u)$
in which the vector u is directed to the convex side from the curve
$(q,u)$
in which the vector u is directed to the convex side from the curve
![]() $\gamma $
.
$\gamma $
.
Remark 1.17. The domain
![]() $\Gamma ^0$
is
$\Gamma ^0$
is
![]() $\beta $
-invariant. It is a topological disk (cylinder) if
$\beta $
-invariant. It is a topological disk (cylinder) if
![]() $\gamma $
is parameterized by an interval (circle). The domain
$\gamma $
is parameterized by an interval (circle). The domain
![]() $\Gamma ^0_+$
is a topological disk (cylinder) adjacent to
$\Gamma ^0_+$
is a topological disk (cylinder) adjacent to
![]() $\widetilde {\gamma }$
.
$\widetilde {\gamma }$
.
Let
![]() $\Pi _\gamma $
denote the open subset of the space of oriented lines in
$\Pi _\gamma $
denote the open subset of the space of oriented lines in
![]() ${\mathbb R}^2$
consisting of the lines
${\mathbb R}^2$
consisting of the lines
![]() $L(q,u)$
with
$L(q,u)$
with
![]() $(q,u)\in \Gamma ^0_+$
. The mapping
$(q,u)\in \Gamma ^0_+$
. The mapping
![]() ${\Lambda } :(q,u)\mapsto L(q,u)$
is a diffeomorphism
${\Lambda } :(q,u)\mapsto L(q,u)$
is a diffeomorphism
It extends to the set
![]() $\Gamma ^0_+\cup \widetilde {\gamma }$
as a homeomorphism sending each point
$\Gamma ^0_+\cup \widetilde {\gamma }$
as a homeomorphism sending each point
![]() $(s,\dot \gamma (s))\in \widetilde {\gamma }$
to the tangent line
$(s,\dot \gamma (s))\in \widetilde {\gamma }$
to the tangent line
![]() $T_s\gamma $
directed by
$T_s\gamma $
directed by
![]() $\dot \gamma (s)$
.
$\dot \gamma (s)$
.
Remark 1.18. Let
![]() ${\mathcal T}$
denote the billiard ball map given by reflection from the curve
${\mathcal T}$
denote the billiard ball map given by reflection from the curve
![]() $\gamma $
acting on oriented lines. It is well known that the billiard ball map
$\gamma $
acting on oriented lines. It is well known that the billiard ball map
![]() ${\mathcal T}$
restricted to
${\mathcal T}$
restricted to
![]() $\Pi _\gamma $
is conjugated by
$\Pi _\gamma $
is conjugated by
![]() ${\Lambda } $
to the product of two involutions
${\Lambda } $
to the product of two involutions
If the curve
![]() $\gamma $
is
$\gamma $
is
![]() $C^{\infty }$
-smooth, then both involutions I and
$C^{\infty }$
-smooth, then both involutions I and
![]() $\beta $
are
$\beta $
are
![]() $C^{\infty }$
-smooth on
$C^{\infty }$
-smooth on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma ^0$
respectively. Their product is well defined and smooth on
$\Gamma ^0$
respectively. Their product is well defined and smooth on
![]() $\Gamma ^0$
and fixes the points of the curve
$\Gamma ^0$
and fixes the points of the curve
![]() $\widetilde {\gamma }$
. Both involutions preserve the canonical symplectic form
$\widetilde {\gamma }$
. Both involutions preserve the canonical symplectic form
![]() $\sin \phi ds\wedge d\phi $
on
$\sin \phi ds\wedge d\phi $
on
![]() $\Gamma \setminus \widetilde {\gamma }$
, which is known to be the
$\Gamma \setminus \widetilde {\gamma }$
, which is known to be the
![]() ${\Lambda } $
-pullback of the standard symplectic form on the space of oriented lines. See [Reference Arnold2, Reference Arnold3, Reference Marvizi and Melrose16–Reference Melrose18, Reference Tabachnikov20]; see also [Reference Glutsyuk10, §7.1].
${\Lambda } $
-pullback of the standard symplectic form on the space of oriented lines. See [Reference Arnold2, Reference Arnold3, Reference Marvizi and Melrose16–Reference Melrose18, Reference Tabachnikov20]; see also [Reference Glutsyuk10, §7.1].
Let us recall another representation of the billiard ball map
![]() ${\mathcal T}$
in a chart where it preserves the standard symplectic form. To do this, consider the orthogonal projection
${\mathcal T}$
in a chart where it preserves the standard symplectic form. To do this, consider the orthogonal projection
![]() ${\pi _\perp :(T{\mathbb R}^2)|_\gamma \to T\gamma }$
sending each vector
${\pi _\perp :(T{\mathbb R}^2)|_\gamma \to T\gamma }$
sending each vector
![]() $u\in T_q{\mathbb R}^2$
with
$u\in T_q{\mathbb R}^2$
with
![]() $q\in \gamma $
to its orthogonal projection to the tangent line
$q\in \gamma $
to its orthogonal projection to the tangent line
![]() $T_q\gamma $
. It projects the unit tangent bundle
$T_q\gamma $
. It projects the unit tangent bundle
![]() $\Gamma $
to the unit ball bundle
$\Gamma $
to the unit ball bundle
A tangent vector
![]() $w = w ({\partial }/{\partial s})\in T_q\gamma $
will be identified with its coordinate
$w = w ({\partial }/{\partial s})\in T_q\gamma $
will be identified with its coordinate
![]() $w=\pm \lVert w\rVert $
in the basic vector
$w=\pm \lVert w\rVert $
in the basic vector
![]() ${\partial }/{\partial s}$
. Thus,
${\partial }/{\partial s}$
. Thus,
![]() $\pi _\perp (s,\phi )=(s,\cos \phi )$
. Consider the following function and differential 2-form on
$\pi _\perp (s,\phi )=(s,\cos \phi )$
. Consider the following function and differential 2-form on
![]() $T\gamma $
:
$T\gamma $
:
The form
![]() $\omega $
coincides with the standard symplectic form on the tangent bundle
$\omega $
coincides with the standard symplectic form on the tangent bundle
![]() $T\gamma $
of the curve
$T\gamma $
of the curve
![]() $\gamma $
(considered as a Riemannian manifold equipped with the metric
$\gamma $
(considered as a Riemannian manifold equipped with the metric
![]() $\lvert ds\rvert ^2$
coming from the standard Euclidean metric on
$\lvert ds\rvert ^2$
coming from the standard Euclidean metric on
![]() ${\mathbb R}^2$
).
${\mathbb R}^2$
).
The curve
![]() $\widetilde {\gamma }=\{(s,\dot \gamma (s)) \mid s\in \gamma \}= \{ w=1\}=\{ y=0\}\subset T\gamma $
is a component of the boundary
$\widetilde {\gamma }=\{(s,\dot \gamma (s)) \mid s\in \gamma \}= \{ w=1\}=\{ y=0\}\subset T\gamma $
is a component of the boundary
![]() $\partial T_{\leq 1}\gamma $
. The projection
$\partial T_{\leq 1}\gamma $
. The projection
![]() $\pi _\perp $
sends
$\pi _\perp $
sends
![]() $\Gamma ^0_+$
diffeomorphically to a domain in
$\Gamma ^0_+$
diffeomorphically to a domain in
![]() $T_{\leq 1}\gamma $
adjacent to
$T_{\leq 1}\gamma $
adjacent to
![]() $\widetilde {\gamma }$
. It extends homeomorphically to
$\widetilde {\gamma }$
. It extends homeomorphically to
![]() $\Gamma ^0_+\cup \widetilde {\gamma }$
as the identity map
$\Gamma ^0_+\cup \widetilde {\gamma }$
as the identity map
![]() $\mathrm {Id}:\widetilde {\gamma }\to \widetilde {\gamma }$
. Let
$\mathrm {Id}:\widetilde {\gamma }\to \widetilde {\gamma }$
. Let
![]() $\mu _+: \pi _\perp (\Gamma ^0_+\cup \widetilde {\gamma })\to \Gamma ^0_+\cup \widetilde {\gamma }$
be the inverse to the restriction of the projection
$\mu _+: \pi _\perp (\Gamma ^0_+\cup \widetilde {\gamma })\to \Gamma ^0_+\cup \widetilde {\gamma }$
be the inverse to the restriction of the projection
![]() $\pi _\perp $
to
$\pi _\perp $
to
![]() $\Gamma ^0_+\cup \widetilde {\gamma }$
. Set
$\Gamma ^0_+\cup \widetilde {\gamma }$
. Set
Theorem 1.19. [Reference Tabachnikov20, §1.5], [Reference Arnold2, Reference Arnold3, Reference Melrose17, Reference Melrose18]; see also [Reference Glutsyuk10, Theorem 7.3]
The mapping
![]() ${\delta _+:\pi _\perp (\Gamma ^0_+)\to T_{\leq 1}\gamma }$
given by equation (1.3), is symplectic: it preserves the form
${\delta _+:\pi _\perp (\Gamma ^0_+)\to T_{\leq 1}\gamma }$
given by equation (1.3), is symplectic: it preserves the form
![]() $\omega =ds\wedge dy$
.
$\omega =ds\wedge dy$
.
Proposition 1.20. [Reference Glutsyuk10, Proposition 7.5]
Let
![]() $\kappa (s)$
denote the (geodesic) curvature of the curve
$\kappa (s)$
denote the (geodesic) curvature of the curve
![]() $\gamma $
. The involutions I,
$\gamma $
. The involutions I,
![]() $\beta $
and the mappings
$\beta $
and the mappings
![]() $\widetilde {\delta }_+$
,
$\widetilde {\delta }_+$
,
![]() $\delta _+$
admit the following (asymptotic) formulas:
$\delta _+$
admit the following (asymptotic) formulas:
The asymptotics are uniform on compact subsets of points
![]() $s\in \gamma $
, as
$s\in \gamma $
, as
![]() $\phi \to 0$
(respectively, as
$\phi \to 0$
(respectively, as
![]() $y\to 0$
).
$y\to 0$
).
Case (2). Let
![]() $\gamma $
be parameterized by an interval, but now it does not necessarily go to infinity or bound a region in the plane. Moreover, we allow
$\gamma $
be parameterized by an interval, but now it does not necessarily go to infinity or bound a region in the plane. Moreover, we allow
![]() $\gamma $
to be an immersed curve that may self-intersect. In this case, some lines
$\gamma $
to be an immersed curve that may self-intersect. In this case, some lines
![]() $L(q,u)$
may intersect
$L(q,u)$
may intersect
![]() $\gamma $
at more than two points. Now the definition of the subset
$\gamma $
at more than two points. Now the definition of the subset
![]() $\Gamma ^0\subset \Gamma $
should be modified to be the subset of those
$\Gamma ^0\subset \Gamma $
should be modified to be the subset of those
![]() $(q,u)\in \Gamma $
for which either
$(q,u)\in \Gamma $
for which either
![]() $u=\dot \gamma (q)$
or there exists a
$u=\dot \gamma (q)$
or there exists a
![]() $q'\in \gamma \cap L(q,u)$
satisfying the condition (b) from Case (1) and such that the arc
$q'\in \gamma \cap L(q,u)$
satisfying the condition (b) from Case (1) and such that the arc
![]() $qq'\subset \gamma $
is disjoint from the line
$qq'\subset \gamma $
is disjoint from the line
![]() $L(q,u)$
, injectively immersed (that is, without self-intersections) and satisfies the statement that the orienting tangent vector
$L(q,u)$
, injectively immersed (that is, without self-intersections) and satisfies the statement that the orienting tangent vector
![]() $\dot \gamma $
at each point has acute angle with
$\dot \gamma $
at each point has acute angle with
![]() $L(q,u)$
. (Here q and
$L(q,u)$
. (Here q and
![]() $q'$
may not be the only points of intersection
$q'$
may not be the only points of intersection
![]() $\gamma \cap L(q,u)$
. If
$\gamma \cap L(q,u)$
. If
![]() $u=\dot \gamma (q)$
, then we set
$u=\dot \gamma (q)$
, then we set
![]() $q'=q$
.)
$q'=q$
.)
Remark 1.21. For any given
![]() $(q,u)\in \Gamma ^0$
, the point
$(q,u)\in \Gamma ^0$
, the point
![]() $q'$
satisfying the conditions from the above paragraph exists whenever u is close enough to
$q'$
satisfying the conditions from the above paragraph exists whenever u is close enough to
![]() $\dot \gamma (q)$
(depending on q). Whenever it exists, it is unique. All the statements and discussion in the previous Case (1) remain valid in our Case (2). Now the mapping
$\dot \gamma (q)$
(depending on q). Whenever it exists, it is unique. All the statements and discussion in the previous Case (1) remain valid in our Case (2). Now the mapping
![]() $\Lambda $
is a local diffeomorphism but not necessarily a global diffeomorphism: an oriented line intersecting
$\Lambda $
is a local diffeomorphism but not necessarily a global diffeomorphism: an oriented line intersecting
![]() $\gamma $
at more than two points (if any) may correspond to at least two different tuples
$\gamma $
at more than two points (if any) may correspond to at least two different tuples
![]() $(q,u)\in \Gamma ^0_+$
.
$(q,u)\in \Gamma ^0_+$
.
1.4 Generalization to
 $C^{\infty }$
-lifted strongly billiard-like maps
$C^{\infty }$
-lifted strongly billiard-like maps
In this subsection and in what follows, we study the next class of area-preserving mappings introduced in [Reference Glutsyuk10] generalizing the billiard maps in equation (1.6).
Definition 1.22. (See [Reference Glutsyuk10, Definition 7.6])
Let
![]() $(a,b)$
be a (may be (semi) infinite) interval in
$(a,b)$
be a (may be (semi) infinite) interval in
![]() ${\mathbb R}$
with coordinate s. Let
${\mathbb R}$
with coordinate s. Let
![]() $V\subset {\mathbb R}\times {\mathbb R}_{+}$
be a domain adjacent to the interval
$V\subset {\mathbb R}\times {\mathbb R}_{+}$
be a domain adjacent to the interval
![]() ${J:=(a,b)\times \{0\}}$
. A mapping
${J:=(a,b)\times \{0\}}$
. A mapping
![]() $F:V\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}\subset {\mathbb R}^2_{s,y}$
is called billiard-like if it satisfies the following conditions:
$F:V\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}\subset {\mathbb R}^2_{s,y}$
is called billiard-like if it satisfies the following conditions:
-
(i)
 $F: V\cup J\to F(V\cup J)$
is a homeomorphism fixing the points in J;
$F: V\cup J\to F(V\cup J)$
is a homeomorphism fixing the points in J; -
(ii)
 $F|_V$
is a diffeomorphism preserving the standard area form
$F|_V$
is a diffeomorphism preserving the standard area form
 $ds\wedge dy$
;
$ds\wedge dy$
; -
(iii) F has the asymptotics of the type
(1.7) $$ \begin{align} F(s,y)=(s+w(s)\sqrt y+O(y),y+O(y^{3/2})) \quad\text{as } y\to0;\quad w(s)>0, \end{align} $$
$$ \begin{align} F(s,y)=(s+w(s)\sqrt y+O(y),y+O(y^{3/2})) \quad\text{as } y\to0;\quad w(s)>0, \end{align} $$
uniformly on compact subsets in the s-interval
 $(a,b)$
;
$(a,b)$
; -
(iv) the variable change
 $$ \begin{align*} (s,y)\mapsto (s,z), \quad z=\sqrt y>0 \end{align*} $$
$$ \begin{align*} (s,y)\mapsto (s,z), \quad z=\sqrt y>0 \end{align*} $$
conjugates F to a smooth map
 $\widetilde {F}(s,z)$
(called its lifting) that is also smooth at points of the boundary interval J; thus,
$\widetilde {F}(s,z)$
(called its lifting) that is also smooth at points of the boundary interval J; thus,
 $w(s)$
is continuous on
$w(s)$
is continuous on
 $(a,b)$
.
$(a,b)$
.
If, in addition to conditions (i)–(iv), the latter mapping
![]() $\widetilde {F}$
is a product of two involutions I and
$\widetilde {F}$
is a product of two involutions I and
![]() $\beta $
fixing the points of the line
$\beta $
fixing the points of the line
![]() $z=0$
,
$z=0$
,
then F will be called a (strongly) billiard-like map.
If F is strongly billiard-like, and the corresponding involution
![]() $\beta $
(or equivalently, the conjugate map
$\beta $
(or equivalently, the conjugate map
![]() $\widetilde {F}$
) is
$\widetilde {F}$
) is
![]() $C^{\infty }$
-smooth and also
$C^{\infty }$
-smooth and also
![]() $C^{\infty }$
-smooth at the points of the boundary interval J, then F is called
$C^{\infty }$
-smooth at the points of the boundary interval J, then F is called
![]() $C^{\infty }$
-lifted. The above definitions make sense for F being a germ of map at the interval J.
$C^{\infty }$
-lifted. The above definitions make sense for F being a germ of map at the interval J.
Example 1.23. The mapping
![]() $\delta _+$
from equation (1.6) is strongly billiard-like in the coordinates
$\delta _+$
from equation (1.6) is strongly billiard-like in the coordinates
![]() $(s,y)$
with
$(s,y)$
with
![]() $w(s)=2\sqrt 2\kappa ^{-1}(s)$
, see equations (1.4), (1.5), and (1.6). If the curve
$w(s)=2\sqrt 2\kappa ^{-1}(s)$
, see equations (1.4), (1.5), and (1.6). If the curve
![]() $\gamma $
is
$\gamma $
is
![]() $C^{\infty }$
-smooth, then
$C^{\infty }$
-smooth, then
![]() $\beta $
and hence
$\beta $
and hence
![]() $\widetilde {\delta }_+=I\circ \beta $
are
$\widetilde {\delta }_+=I\circ \beta $
are
![]() $C^{\infty }$
-smooth, and hence,
$C^{\infty }$
-smooth, and hence,
![]() $\delta _+$
is
$\delta _+$
is
![]() $C^{\infty }$
-lifted.
$C^{\infty }$
-lifted.
Proposition 1.24. The class of (germs at J of)
![]() $C^{\infty }$
-lifted strongly billiard-like maps is invariant under conjugacy by (germs at J of)
$C^{\infty }$
-lifted strongly billiard-like maps is invariant under conjugacy by (germs at J of)
![]() $C^{\infty }$
-smooth symplectomorphisms
$C^{\infty }$
-smooth symplectomorphisms
![]() $G:V\cup J\to G(V\cup J)\subset {\mathbb R}\times {\mathbb R}_{\geq 0}$
sending J onto an interval in
$G:V\cup J\to G(V\cup J)\subset {\mathbb R}\times {\mathbb R}_{\geq 0}$
sending J onto an interval in
![]() ${\mathbb R}\times \{0\}$
. Here,
${\mathbb R}\times \{0\}$
. Here,
![]() $V\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J.
$V\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J.
Proof. Let F be a
![]() $C^{\infty }$
-lifted strongly billiard-like map and
$C^{\infty }$
-lifted strongly billiard-like map and
![]() $\widetilde {F}=I\circ \beta $
be its lifting. Let
$\widetilde {F}=I\circ \beta $
be its lifting. Let
![]() $V\subset {\mathbb R}\times {\mathbb R}_+$
be a domain adjacent to J. Let F be defined on
$V\subset {\mathbb R}\times {\mathbb R}_+$
be a domain adjacent to J. Let F be defined on
![]() $V\cup J$
, and let
$V\cup J$
, and let
![]() $G:V\cup J\to G(V\cup J)\subset {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a
$G:V\cup J\to G(V\cup J)\subset {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a
![]() $C^{\infty }$
-smooth symplectomorphism as above. Let us denote
$C^{\infty }$
-smooth symplectomorphism as above. Let us denote
![]() $G(s,y)=(\widehat {s}(s,y), \widehat {y}(s,y))$
. One has
$G(s,y)=(\widehat {s}(s,y), \widehat {y}(s,y))$
. One has
![]() $\widehat {y}(s,0)\equiv 0$
,
$\widehat {y}(s,0)\equiv 0$
,
![]() ${\partial \widehat {s}}(s,0)/{\partial s}> 0$
,
${\partial \widehat {s}}(s,0)/{\partial s}> 0$
,
![]() ${\partial \widehat {y}}(s,0)/{\partial y}>0$
, by definition and orientation-preserving property (symplecticity). Thus,
${\partial \widehat {y}}(s,0)/{\partial y}>0$
, by definition and orientation-preserving property (symplecticity). Thus,
![]() $\widehat {y}(s,y)=yg(s,y)$
, where
$\widehat {y}(s,y)=yg(s,y)$
, where
![]() $g(s,y)$
is a positive
$g(s,y)$
is a positive
![]() $C^{\infty }$
-smooth function on a neighborhood of the interval J in
$C^{\infty }$
-smooth function on a neighborhood of the interval J in
![]() $({\mathbb R}\times {\mathbb R}_{>0})\cup J$
. The lifting
$({\mathbb R}\times {\mathbb R}_{>0})\cup J$
. The lifting
![]() $\widetilde {G}$
of the map G to the variables
$\widetilde {G}$
of the map G to the variables
![]() $(s,z)$
,
$(s,z)$
,
![]() $z=\sqrt y$
, acts as follows:
$z=\sqrt y$
, acts as follows:
The latter square root is well defined and
![]() $C^{\infty }$
-smooth. This implies that the map
$C^{\infty }$
-smooth. This implies that the map
![]() $\widetilde {G}$
is a
$\widetilde {G}$
is a
![]() $C^{\infty }$
-smooth diffeomorphism of domains with arcs of boundaries corresponding to
$C^{\infty }$
-smooth diffeomorphism of domains with arcs of boundaries corresponding to
![]() $V\cup J$
and
$V\cup J$
and
![]() $G(V\cup J)$
. Hence, the lifting
$G(V\cup J)$
. Hence, the lifting
![]() $\widetilde {G}\circ \widetilde {F}\circ \widetilde {G}^{-1}$
of the conjugate
$\widetilde {G}\circ \widetilde {F}\circ \widetilde {G}^{-1}$
of the conjugate
![]() $F_G:=G\circ F\circ G^{-1}$
is a
$F_G:=G\circ F\circ G^{-1}$
is a
![]() $C^{\infty }$
-smooth diffeomorphism that is the product of
$C^{\infty }$
-smooth diffeomorphism that is the product of
![]() $\widetilde {G}$
-conjugates of the involutions I and
$\widetilde {G}$
-conjugates of the involutions I and
![]() $\beta $
. One has
$\beta $
. One has
![]() $\widetilde {G}\circ I\circ \widetilde {G}^{-1}=I$
, by equation (1.9);
$\widetilde {G}\circ I\circ \widetilde {G}^{-1}=I$
, by equation (1.9);
![]() $F_G$
is a symplectomorphism, since so are F and G;
$F_G$
is a symplectomorphism, since so are F and G;
by diffeomorphicity. Substituting equations (1.10) and (1.7) to the expression
![]() $F_G=G\circ F\circ G^{-1}$
and denoting
$F_G=G\circ F\circ G^{-1}$
and denoting
![]() $(s,0):=G^{-1}(\widehat {s},0)$
, we get
$(s,0):=G^{-1}(\widehat {s},0)$
, we get
 $$ \begin{align*} F_G(\widehat{s},\widehat{y})=\bigg(\widehat{s}+ \frac{\partial\widehat{s}}{\partial s}(s,0)w(s)g^{-(1/2)}(s,0) (\widehat{y})^{1/2}+O(\widehat{y}), \widehat{y}+O(\widehat{y}^{3/2})\bigg). \end{align*} $$
$$ \begin{align*} F_G(\widehat{s},\widehat{y})=\bigg(\widehat{s}+ \frac{\partial\widehat{s}}{\partial s}(s,0)w(s)g^{-(1/2)}(s,0) (\widehat{y})^{1/2}+O(\widehat{y}), \widehat{y}+O(\widehat{y}^{3/2})\bigg). \end{align*} $$
This implies that the conjugate
![]() $F_G$
has type of equation (1.7) and hence is strongly billiard-like. This proves the proposition.
$F_G$
has type of equation (1.7) and hence is strongly billiard-like. This proves the proposition.
Convention 1.25. Let
![]() $J=(a,b)\times \{0\}\subset {\mathbb R}^2_{x,y}$
. Let
$J=(a,b)\times \{0\}\subset {\mathbb R}^2_{x,y}$
. Let
![]() $U\subset \{ y>0\}$
be a domain adjacent to J. Let
$U\subset \{ y>0\}$
be a domain adjacent to J. Let
![]() $F:U\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a map fixing all the points of the interval J. Let
$F:U\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a map fixing all the points of the interval J. Let
![]() $\widetilde {h}:U\cup J\to {\mathbb R}_{\geq 0}$
be a
$\widetilde {h}:U\cup J\to {\mathbb R}_{\geq 0}$
be a
![]() $C^{\infty }$
-smooth F-invariant function, that is,
$C^{\infty }$
-smooth F-invariant function, that is,
![]() $\widetilde {h}(z)=\widetilde {h}\circ F(z)$
whenever
$\widetilde {h}(z)=\widetilde {h}\circ F(z)$
whenever
![]() $z,F(z)\in U\cup J$
, and let
$z,F(z)\in U\cup J$
, and let
 $$ \begin{align} \widetilde{h}|_J\equiv 0,\quad \frac{\partial\widetilde{h}}{\partial y}>0. \end{align} $$
$$ \begin{align} \widetilde{h}|_J\equiv 0,\quad \frac{\partial\widetilde{h}}{\partial y}>0. \end{align} $$
Let
![]() $\widetilde {h}=\mathrm {const.}$
denote the foliation by connected components of level curves of the function
$\widetilde {h}=\mathrm {const.}$
denote the foliation by connected components of level curves of the function
![]() $\widetilde {h}$
. This is a
$\widetilde {h}$
. This is a
![]() $C^\infty $
-smooth foliation on
$C^\infty $
-smooth foliation on
![]() $U\cup J$
, with J being a leaf. It will be called a foliation by F-invariant curves.
$U\cup J$
, with J being a leaf. It will be called a foliation by F-invariant curves.
Theorem 1.26. For every
![]() $C^{\infty }$
-lifted strongly billiard-like map F, there exists a domain U adjacent to J such that
$C^{\infty }$
-lifted strongly billiard-like map F, there exists a domain U adjacent to J such that
![]() $U\cup J$
admits a
$U\cup J$
admits a
![]() $C^{\infty }$
-smooth F-invariant function
$C^{\infty }$
-smooth F-invariant function
![]() $\widetilde {h}$
satisfying equation (1.11); thus,
$\widetilde {h}$
satisfying equation (1.11); thus,
![]() $\widetilde {h}=\mathrm {const.}$
is a foliation by F-invariant curves. Moreover, U can be chosen so that there is an infinite-dimensional family of foliations as above with distinct boundary germs.
$\widetilde {h}=\mathrm {const.}$
is a foliation by F-invariant curves. Moreover, U can be chosen so that there is an infinite-dimensional family of foliations as above with distinct boundary germs.
Theorem 1.27. For every function
![]() $\widetilde {h}$
from Theorem 1.26, replacing it by its post-composition with a
$\widetilde {h}$
from Theorem 1.26, replacing it by its post-composition with a
![]() $C^\infty $
-smooth function of one variable (which does not change the foliation
$C^\infty $
-smooth function of one variable (which does not change the foliation
![]() $\widetilde {h}=\mathrm {const.}$
) one can achieve that there exists a
$\widetilde {h}=\mathrm {const.}$
) one can achieve that there exists a
![]() $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
![]() $\tau =\tau (s,y)$
and a domain
$\tau =\tau (s,y)$
and a domain
![]() $U\subset \{ y>0\}$
adjacent to J such that
$U\subset \{ y>0\}$
adjacent to J such that
![]() $(\tau ,\widetilde {h})$
are symplectic coordinates on
$(\tau ,\widetilde {h})$
are symplectic coordinates on
![]() $U\cup J$
and in these coordinates,
$U\cup J$
and in these coordinates,
Definition 1.28. Let
![]() $V\subset {\mathbb R}\times {\mathbb R}_{+}\subset {\mathbb R}^2_{s,y}$
be a domain adjacent to an interval
$V\subset {\mathbb R}\times {\mathbb R}_{+}\subset {\mathbb R}^2_{s,y}$
be a domain adjacent to an interval
![]() ${J=(a,b)\times \{0\}}$
. A
${J=(a,b)\times \{0\}}$
. A
![]() $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
![]() $f(s,y)$
on
$f(s,y)$
on
![]() $V\cup J$
is y-flat, if it vanishes on J together with all its partial derivatives in
$V\cup J$
is y-flat, if it vanishes on J together with all its partial derivatives in
![]() $(s,y)$
; that is, f has trivial jets of all orders at each point in J. (In this case, the function
$(s,y)$
; that is, f has trivial jets of all orders at each point in J. (In this case, the function
![]() $f(s,y)$
and each of its derivatives converge to zero uniformly on compact subsets in the s-interval
$f(s,y)$
and each of its derivatives converge to zero uniformly on compact subsets in the s-interval
![]() $(a,b)$
, as
$(a,b)$
, as
![]() $y\to 0$
, by continuity.)
$y\to 0$
, by continuity.)
Remark 1.29. In the conditions of the above definition, let
![]() $(x,h)$
be new
$(x,h)$
be new
![]() $C^{\infty }$
-smooth coordinates on
$C^{\infty }$
-smooth coordinates on
![]() $V\cup J$
with
$V\cup J$
with
![]() $h(s,0)\equiv 0$
. Then each y-flat function is h-flat and vice versa. This follows from definition.
$h(s,0)\equiv 0$
. Then each y-flat function is h-flat and vice versa. This follows from definition.
The proof of Theorem 1.26 uses the result of Marvizi and Melrose [Reference Marvizi and Melrose16, Theorem 3.2] stating a formal analogue of Theorem 1.26: the existence of an F-invariant formal power series
![]() $\sum _{k=1}^{+\infty }h_k(s)y^k$
, see Theorem 2.1. It implies that in appropriate coordinates
$\sum _{k=1}^{+\infty }h_k(s)y^k$
, see Theorem 2.1. It implies that in appropriate coordinates
![]() $(\tau ,h)$
, the map F takes the form
$(\tau ,h)$
, the map F takes the form
![]() $F(\tau ,h)=(\tau +\sqrt h+{\operatorname {flat}}(h), h+{\operatorname {flat}}(h))$
. Here,
$F(\tau ,h)=(\tau +\sqrt h+{\operatorname {flat}}(h), h+{\operatorname {flat}}(h))$
. Here,
![]() ${\operatorname {flat}}(h)$
is an h-flat function, see the above definition. In the coordinates
${\operatorname {flat}}(h)$
is an h-flat function, see the above definition. In the coordinates
![]() $(\tau ,\phi )$
,
$(\tau ,\phi )$
,
![]() $\phi =\sqrt h$
, the lifted map
$\phi =\sqrt h$
, the lifted map
![]() $\widetilde {F}$
takes the form
$\widetilde {F}$
takes the form
We prove the existence of a
![]() $C^{\infty }$
-smooth
$C^{\infty }$
-smooth
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
![]() $\widetilde {\phi }$
with
$\widetilde {\phi }$
with
![]() $\widetilde {\phi }-\phi ={\operatorname {flat}}(\phi )$
(the next theorem), and then deduce the existence statements in Theorems 1.26, 1.9, and 1.12.
$\widetilde {\phi }-\phi ={\operatorname {flat}}(\phi )$
(the next theorem), and then deduce the existence statements in Theorems 1.26, 1.9, and 1.12.
Theorem 1.30. Let
![]() $V\kern1.3pt{\subset}\kern1.3pt {\mathbb R}_{\tau }\kern1.3pt{\times}\kern1.3pt ({\mathbb R}_+)_{\phi }$
be a domain adjacent to an interval
$V\kern1.3pt{\subset}\kern1.3pt {\mathbb R}_{\tau }\kern1.3pt{\times}\kern1.3pt ({\mathbb R}_+)_{\phi }$
be a domain adjacent to an interval
![]() ${J\kern1.3pt{=}\kern1.3pt(a,b)\kern1.3pt{\times}\kern1.3pt \{0\}}$
. Let
${J\kern1.3pt{=}\kern1.3pt(a,b)\kern1.3pt{\times}\kern1.3pt \{0\}}$
. Let
![]() $\widetilde {F}:V\cup J\to {\mathbb R}_{\tau }\times ({\mathbb R}_{\geq 0})_{\phi }$
be a
$\widetilde {F}:V\cup J\to {\mathbb R}_{\tau }\times ({\mathbb R}_{\geq 0})_{\phi }$
be a
![]() $C^{\infty }$
-smooth mapping of the type in equation (1.13). (Here we do not assume any area-preserving property.)
$C^{\infty }$
-smooth mapping of the type in equation (1.13). (Here we do not assume any area-preserving property.)
-
(1) There exists a domain
 $W\subset V$
adjacent to J and an
$W\subset V$
adjacent to J and an
 $\widetilde {F}$
-invariant
$\widetilde {F}$
-invariant
 $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
 $\widetilde {\phi }$
on
$\widetilde {\phi }$
on
 $W\cup J$
of the type
$W\cup J$
of the type
 $\widetilde {\phi }(\tau ,\phi )=\phi +{\operatorname {flat}}(\phi )$
;
$\widetilde {\phi }(\tau ,\phi )=\phi +{\operatorname {flat}}(\phi )$
;
 $({\partial \widetilde {\phi }}/{\partial \phi })> 0$
.
$({\partial \widetilde {\phi }}/{\partial \phi })> 0$
. -
(2) For every function
 $\widetilde {\phi }$
as above, one can shrink the domain W (keeping it adjacent to J) so that there exists a
$\widetilde {\phi }$
as above, one can shrink the domain W (keeping it adjacent to J) so that there exists a
 $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
 $\widetilde {\tau }(\tau ,\phi )=\tau +{\operatorname {flat}}(\phi )$
such that the map
$\widetilde {\tau }(\tau ,\phi )=\tau +{\operatorname {flat}}(\phi )$
such that the map
 $(\tau ,\phi )\mapsto (\widetilde {\tau },\widetilde {\phi })$
is a
$(\tau ,\phi )\mapsto (\widetilde {\tau },\widetilde {\phi })$
is a
 $C^{\infty }$
-smooth diffeomorphism on
$C^{\infty }$
-smooth diffeomorphism on
 $W\cup J$
that conjugates
$W\cup J$
that conjugates
 $\widetilde {F}$
to the map (1.14)
$\widetilde {F}$
to the map (1.14) $$ \begin{align} \widehat{F}: (\widetilde{\tau},\widetilde{\phi})\mapsto(\widetilde{\tau}+\widetilde{\phi},\widetilde{\phi}). \end{align} $$
$$ \begin{align} \widehat{F}: (\widetilde{\tau},\widetilde{\phi})\mapsto(\widetilde{\tau}+\widetilde{\phi},\widetilde{\phi}). \end{align} $$
-
(3) There exists a continuum of functions
 $\widetilde {\phi }$
satisfying statement (1) such that the corresponding foliations
$\widetilde {\phi }$
satisfying statement (1) such that the corresponding foliations
 $\widetilde {\phi }=\mathrm {const.}$
are
$\widetilde {\phi }=\mathrm {const.}$
are
 $C^{\infty }$
-smooth on the same subset
$C^{\infty }$
-smooth on the same subset
 $W\cup J$
and form an infinite-dimensional family of foliations with distinct boundary germs.
$W\cup J$
and form an infinite-dimensional family of foliations with distinct boundary germs.
1.5 Unique determination of jets. Space of germs of foliations. Non-uniqueness
Theorem 1.31. All the germs of foliations satisfying the statements of any of Theorems 1.9, 1.12, 1.13, 1.26, and 1.30 at the corresponding boundary curve
![]() $\gamma $
, J are flatly close to each other near the boundary. That is, they have the same n-jet for every n at each point of the boundary.
$\gamma $
, J are flatly close to each other near the boundary. That is, they have the same n-jet for every n at each point of the boundary.
The statement of Theorem 1.31 follows from the result of Marvizi and Melrose [Reference Marvizi and Melrose16, Theorem 3.2] recalled below as Theorem 2.1. For completeness of presentation, we will give a proof of Theorem 1.31 in §2.8.
Let us now describe the space of jets at J of foliations satisfying the statements of Theorem 1.26. Recall that there exist coordinates
![]() $(\tau ,\widetilde {h})$
in which
$(\tau ,\widetilde {h})$
in which
![]() $J=\{\widetilde {h}=0\}$
and F acts as in equation (1.12):
$J=\{\widetilde {h}=0\}$
and F acts as in equation (1.12):
![]() $F:(\tau ,\widetilde {h})\mapsto (\tau +\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}},\widetilde {h})$
. Fix these coordinates
$F:(\tau ,\widetilde {h})\mapsto (\tau +\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}},\widetilde {h})$
. Fix these coordinates
![]() $(\tau ,\widetilde {h})$
. Without loss of generality, we consider that
$(\tau ,\widetilde {h})$
. Without loss of generality, we consider that
![]() $0\in J$
.
$0\in J$
.
Consider the foliation
![]() $\widetilde {h}=\mathrm {const}$
. Let
$\widetilde {h}=\mathrm {const}$
. Let
![]() ${\mathcal F}$
be another
${\mathcal F}$
be another
![]() $C^\infty $
-smooth foliation by F-invariant curves defined on a domain V in the upper half-plane
$C^\infty $
-smooth foliation by F-invariant curves defined on a domain V in the upper half-plane
![]() $\{\widetilde {h}>0\}$
adjacent to J that extends
$\{\widetilde {h}>0\}$
adjacent to J that extends
![]() $C^\infty $
-smoothly to J with J being a leaf. It is a foliation by level curves of an F-invariant function
$C^\infty $
-smoothly to J with J being a leaf. It is a foliation by level curves of an F-invariant function
![]() $g(\tau ,\widetilde {h})=\widetilde {h}+{\operatorname {flat}}(\widetilde {h})$
, which follows from Theorem 1.31. We can and will normalize g so that
$g(\tau ,\widetilde {h})=\widetilde {h}+{\operatorname {flat}}(\widetilde {h})$
, which follows from Theorem 1.31. We can and will normalize g so that
Remark 1.32. The above normalization can be achieved by replacing the function g by its post-composition with a function
![]() $\phi +{\operatorname {flat}}(\phi )$
of one variable
$\phi +{\operatorname {flat}}(\phi )$
of one variable
![]() $\phi $
. Each foliation from Theorem 1.26 admits a unique F-invariant first integral g as in equation (1.15) and vice versa: for every F-invariant function g as in equation (1.15), the foliation
$\phi $
. Each foliation from Theorem 1.26 admits a unique F-invariant first integral g as in equation (1.15) and vice versa: for every F-invariant function g as in equation (1.15), the foliation
![]() $g=\mathrm {const.}$
satisfies the statement of Theorem 1.26.
$g=\mathrm {const.}$
satisfies the statement of Theorem 1.26.
Proposition 1.33.
-
(1) For every
 $C^\infty $
-smooth function g on a domain
$C^\infty $
-smooth function g on a domain
 $V\subset \{\widetilde {h}>0\}$
adjacent to J that extends
$V\subset \{\widetilde {h}>0\}$
adjacent to J that extends
 $C^\infty $
-smoothly to J, satisfies equation (1.15), and is invariant under the mapping
$C^\infty $
-smoothly to J, satisfies equation (1.15), and is invariant under the mapping
 $F:(\tau ,\widetilde {h})\mapsto (\tau +\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}},\widetilde {h})$
, there exist a
$F:(\tau ,\widetilde {h})\mapsto (\tau +\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}},\widetilde {h})$
, there exist a
 $\delta>0$
and a unique
$\delta>0$
and a unique
 $C^\infty $
- smooth
$C^\infty $
- smooth
 $\widetilde {h}$
-flat function
$\widetilde {h}$
-flat function
 $\psi (t,\widetilde {h})$
on
$\psi (t,\widetilde {h})$
on
 $S^1\times [0,\delta )$
,
$S^1\times [0,\delta )$
,
 $S^1={\mathbb R}_{t}/ {\mathbb Z}$
such that (1.16)
$S^1={\mathbb R}_{t}/ {\mathbb Z}$
such that (1.16) $$ \begin{align} \!\!\psi(0,\widetilde{h}) =0,\qquad\qquad\qquad \end{align} $$
(1.17)
$$ \begin{align} \!\!\psi(0,\widetilde{h}) =0,\qquad\qquad\qquad \end{align} $$
(1.17) $$ \begin{align} g(\tau,\widetilde{h}) &=\widetilde{h}+\psi\bigg(\frac{\tau}{\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}}},\widetilde{h}\bigg). \end{align} $$
$$ \begin{align} g(\tau,\widetilde{h}) &=\widetilde{h}+\psi\bigg(\frac{\tau}{\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}}},\widetilde{h}\bigg). \end{align} $$
Here we treat
 $\psi (t,\widetilde {h})$
as a function of two variables that is 1-periodic in t. Conversely, for every
$\psi (t,\widetilde {h})$
as a function of two variables that is 1-periodic in t. Conversely, for every
 $\delta>0$
, every
$\delta>0$
, every
 $\widetilde {h}$
-flat function
$\widetilde {h}$
-flat function
 $\psi $
on the cylinder
$\psi $
on the cylinder
 $S^1\times [0,\delta )$
satisfying equation (1.16) corresponds to some function g as above via equation (1.17), defined on
$S^1\times [0,\delta )$
satisfying equation (1.16) corresponds to some function g as above via equation (1.17), defined on
 $V\cup J$
with
$V\cup J$
with
 $J={\mathbb R}\times \{0\}$
and
$J={\mathbb R}\times \{0\}$
and
 $V=\{0<\widetilde {h}<\delta \}$
.
$V=\{0<\widetilde {h}<\delta \}$
. -
(2) The analogous statements hold for the map
 $F:(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
and the function (1.18)
$F:(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
and the function (1.18) $$ \begin{align} g(\tau,\phi)=\phi+\psi\bigg(\frac{\tau}{\phi},\phi\bigg). \end{align} $$
$$ \begin{align} g(\tau,\phi)=\phi+\psi\bigg(\frac{\tau}{\phi},\phi\bigg). \end{align} $$
Theorem 1.34. Every germ at J of
![]() $C^\infty $
-smooth foliation
$C^\infty $
-smooth foliation
![]() ${\mathcal F}$
by invariant curves under a map F of one of the types in equation (1.12) or (1.14) is defined by a unique germ at
${\mathcal F}$
by invariant curves under a map F of one of the types in equation (1.12) or (1.14) is defined by a unique germ at
![]() $S^1\times \{0\}$
of
$S^1\times \{0\}$
of
![]() $C^\infty $
-smooth h-flat function
$C^\infty $
-smooth h-flat function
![]() $\psi (t,h)$
,
$\psi (t,h)$
,
![]() $\psi : S^1\times {\mathbb R}_{\geq 0}\to {\mathbb R}$
,
$\psi : S^1\times {\mathbb R}_{\geq 0}\to {\mathbb R}$
,
![]() $\psi (0,h)=0$
, so that
$\psi (0,h)=0$
, so that
![]() ${\mathcal F}$
is the foliation by level curves of the corresponding function g given by equation (1.17) or (1.18) respectively. Conversely, each germ of function
${\mathcal F}$
is the foliation by level curves of the corresponding function g given by equation (1.17) or (1.18) respectively. Conversely, each germ of function
![]() $\psi $
as above defines a germ of foliation as above at J.
$\psi $
as above defines a germ of foliation as above at J.
Theorem 1.35. The space of germs of foliations satisfy statements of any of Theorems 1.9, 1.12, 1.13, 1.26, and 1.30 at the corresponding boundary curve
![]() $\gamma $
or J is isomorphic to the space of h-flat germs at
$\gamma $
or J is isomorphic to the space of h-flat germs at
![]() $S^1\times \{0\}$
of
$S^1\times \{0\}$
of
![]() $C^\infty $
-smooth functions
$C^\infty $
-smooth functions
![]() $\psi (t,h)$
on
$\psi (t,h)$
on
![]() $S^1\times {\mathbb R}_{\geq 0}$
with
$S^1\times {\mathbb R}_{\geq 0}$
with
![]() $\psi (0,h)=0$
.
$\psi (0,h)=0$
.
Theorems 1.31, 1.34, and 1.35 and Proposition 1.33 will be proved in §2.8. In §2.9, we deduce non-uniqueness statements of Theorems 1.9, 1.12, 1.13, 1.26, and 1.30 from Theorem 1.35 and the following proposition, which will be also proved there.
Proposition 1.36. Let
![]() $J=(a,b)\times \{0\}$
,
$J=(a,b)\times \{0\}$
,
![]() $W\subset {\mathbb R}_\tau \times ({\mathbb R}_+)_\phi $
be a domain adjacent to J. Let
$W\subset {\mathbb R}_\tau \times ({\mathbb R}_+)_\phi $
be a domain adjacent to J. Let
![]() $\widetilde {F}:W\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a map, as in equation (1.13). Any two
$\widetilde {F}:W\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a map, as in equation (1.13). Any two
![]() $\widetilde {F}$
-invariant foliations (functions, line fields) on W having distinct germs at J have distinct germs at each point in J. The same statement holds for similar objects invariant under a
$\widetilde {F}$
-invariant foliations (functions, line fields) on W having distinct germs at J have distinct germs at each point in J. The same statement holds for similar objects invariant under a
![]() $C^{\infty }$
-lifted strongly billiard-like map.
$C^{\infty }$
-lifted strongly billiard-like map.
1.6 Corollaries on conjugacy of open billiard maps near the boundary
The results stated below and proved in §2.10 concern (symplectic) conjugacy of billiard maps near the boundary.
Here we deal with a strictly convex oriented
![]() $C^\infty $
-smooth curve
$C^\infty $
-smooth curve
![]() $\gamma \subset {\mathbb R}^2$
that is not closed: parameterized by an interval. We consider that it is positively oriented as the boundary of its convex side. Let us first consider that
$\gamma \subset {\mathbb R}^2$
that is not closed: parameterized by an interval. We consider that it is positively oriented as the boundary of its convex side. Let us first consider that
![]() $\gamma $
goes to infinity in both directions and bounds a convex open billiard. By
$\gamma $
goes to infinity in both directions and bounds a convex open billiard. By
![]() $\widetilde {\gamma }$
, we denote the family of its orienting unit tangent vectors;
$\widetilde {\gamma }$
, we denote the family of its orienting unit tangent vectors;
![]() $\widetilde {\gamma }$
lies in the space
$\widetilde {\gamma }$
lies in the space
![]() $\Gamma $
, which is the unit tangent bundle of the ambient plane restricted to
$\Gamma $
, which is the unit tangent bundle of the ambient plane restricted to
![]() $\gamma $
. Let s be a natural length parameter of the curve
$\gamma $
. Let s be a natural length parameter of the curve
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\Gamma ^0_+\subset \Gamma $
be the open subset adjacent to
$\Gamma ^0_+\subset \Gamma $
be the open subset adjacent to
![]() $\widetilde {\gamma }$
defined in §1.3. It lies in the space of pairs
$\widetilde {\gamma }$
defined in §1.3. It lies in the space of pairs
![]() $(s,v)$
, where
$(s,v)$
, where
![]() $s\in \gamma $
and
$s\in \gamma $
and
![]() $v\in T_s{\mathbb R}^2$
is a unit vector directed to the convex side from the curve
$v\in T_s{\mathbb R}^2$
is a unit vector directed to the convex side from the curve
![]() $\gamma $
. Recall that
$\gamma $
. Recall that
![]() $\phi =\phi (v)$
denotes the angle between the vector
$\phi =\phi (v)$
denotes the angle between the vector
![]() $v$
and the unit tangent vector
$v$
and the unit tangent vector
![]() $\dot \gamma (s)$
. Let
$\dot \gamma (s)$
. Let
![]() $(a,b)=(a_\gamma ,b_\gamma )\subset {\mathbb R}$
denote the length parameter interval parameterizing
$(a,b)=(a_\gamma ,b_\gamma )\subset {\mathbb R}$
denote the length parameter interval parameterizing
![]() $\gamma $
. In the coordinates
$\gamma $
. In the coordinates
![]() $(s,\phi )$
, the curve
$(s,\phi )$
, the curve
![]() $\widetilde {\gamma }$
is the interval
$\widetilde {\gamma }$
is the interval
![]() $J=J_\gamma =(a,b)\times \{0\}$
, and
$J=J_\gamma =(a,b)\times \{0\}$
, and
![]() $\Gamma ^0_+$
is a domain in
$\Gamma ^0_+$
is a domain in
![]() ${\mathbb R}\times {\mathbb R}_+$
adjacent to J. Set
${\mathbb R}\times {\mathbb R}_+$
adjacent to J. Set
![]() $y=1-\cos \phi $
, see equation (1.2). Recall that the billiard map
$y=1-\cos \phi $
, see equation (1.2). Recall that the billiard map
![]() $\mathcal T_\gamma $
acting by reflection from
$\mathcal T_\gamma $
acting by reflection from
![]() $\gamma $
of the above unit vectors is a
$\gamma $
of the above unit vectors is a
![]() $C^\infty $
-smooth diffeomorphism defined on
$C^\infty $
-smooth diffeomorphism defined on
![]() $\Gamma ^0_+\cup \widetilde {\gamma }$
. In the coordinates
$\Gamma ^0_+\cup \widetilde {\gamma }$
. In the coordinates
![]() $(s,y)$
, it is a symplectic map: a
$(s,y)$
, it is a symplectic map: a
![]() $C^\infty $
-lifted strongly billiard-like map defined on
$C^\infty $
-lifted strongly billiard-like map defined on
![]() $\mathcal V\cup J$
, where
$\mathcal V\cup J$
, where
![]() $\mathcal V\subset {\mathbb R}_s\times ({\mathbb R}_+)_y$
is a domain adjacent to J.
$\mathcal V\subset {\mathbb R}_s\times ({\mathbb R}_+)_y$
is a domain adjacent to J.
The above statements remain valid in the case when the curve
![]() $\gamma $
in question is a subarc (parameterized by interval but not necessarily infinite) of a strictly convex
$\gamma $
in question is a subarc (parameterized by interval but not necessarily infinite) of a strictly convex
![]() $C^\infty $
-smooth curve;
$C^\infty $
-smooth curve;
![]() $\gamma $
also may be an immersed curve.
$\gamma $
also may be an immersed curve.
Definition 1.37. Let
![]() $\gamma _1,\gamma _2\subset {\mathbb R}^2$
be strictly convex
$\gamma _1,\gamma _2\subset {\mathbb R}^2$
be strictly convex
![]() $C^\infty $
-smooth planar curves parameterized by intervals (they are allowed to be immersed), positively oriented as boundaries of their convex sides. Let
$C^\infty $
-smooth planar curves parameterized by intervals (they are allowed to be immersed), positively oriented as boundaries of their convex sides. Let
![]() $J_{\gamma _i}\subset {\mathbb R}\times \{0\}$
,
$J_{\gamma _i}\subset {\mathbb R}\times \{0\}$
,
![]() $i=1,2$
, be the corresponding intervals defined above. We say that the billiard maps
$i=1,2$
, be the corresponding intervals defined above. We say that the billiard maps
![]() $\mathcal T_{\gamma _i}$
are
$\mathcal T_{\gamma _i}$
are
![]() $C^\infty $
-smoothly conjugated near the boundary in the
$C^\infty $
-smoothly conjugated near the boundary in the
![]() $(s,\phi )$
-
$(s,\phi )$
-
![]() $((s,y)\text {-})$
coordinates if there exist domains
$((s,y)\text {-})$
coordinates if there exist domains
![]() $U_i$
in
$U_i$
in
![]() ${\mathbb R}_s\times ({\mathbb R}_+)_\phi $
(respectively, in
${\mathbb R}_s\times ({\mathbb R}_+)_\phi $
(respectively, in
![]() ${\mathbb R}_s\times ({\mathbb R}_+)_y$
) adjacent to
${\mathbb R}_s\times ({\mathbb R}_+)_y$
) adjacent to
![]() $J_{\gamma _i}$
and a
$J_{\gamma _i}$
and a
![]() $C^\infty $
-smooth diffeomorphism
$C^\infty $
-smooth diffeomorphism
![]() $H:U_1\cup J_{\gamma _1}\to U_2\cup J_{\gamma _2}$
conjugating the billiard maps,
$H:U_1\cup J_{\gamma _1}\to U_2\cup J_{\gamma _2}$
conjugating the billiard maps,
![]() $H\circ {\mathcal T}_{\gamma _1}\circ H^{-1}={\mathcal T}_{\gamma _2}$
. In the case when the billiard maps are conjugated in the
$H\circ {\mathcal T}_{\gamma _1}\circ H^{-1}={\mathcal T}_{\gamma _2}$
. In the case when the billiard maps are conjugated in the
![]() $(s,y)$
-coordinates, and the conjugating diffeomorphism H is a symplectomorphism, we say that they are
$(s,y)$
-coordinates, and the conjugating diffeomorphism H is a symplectomorphism, we say that they are
![]() $C^\infty $
-smoothly symplectically conjugated near the boundary.
$C^\infty $
-smoothly symplectically conjugated near the boundary.
Remark 1.38. Smooth conjugacy of billiard maps near the boundary in the coordinates
![]() $(s,y)$
implies their smooth conjugacy in the coordinates
$(s,y)$
implies their smooth conjugacy in the coordinates
![]() $(s,\phi )$
. This follows from the fact that for every two intervals
$(s,\phi )$
. This follows from the fact that for every two intervals
![]() $J_1,J_2\subset {\mathbb R}_s\times \{0\}$
and every two domains
$J_1,J_2\subset {\mathbb R}_s\times \{0\}$
and every two domains
![]() $U_1,U_2\subset {\mathbb R}_s\times ({\mathbb R}_+)_y$
adjacent to
$U_1,U_2\subset {\mathbb R}_s\times ({\mathbb R}_+)_y$
adjacent to
![]() $J_1$
and
$J_1$
and
![]() $J_2$
respectively, every diffeomorphism
$J_2$
respectively, every diffeomorphism
![]() $H:U_1\cup J_1\to U_2\cup J_2$
lifts to a diffeomorphism of the corresponding domains in the
$H:U_1\cup J_1\to U_2\cup J_2$
lifts to a diffeomorphism of the corresponding domains in the
![]() $(s,\phi )$
-coordinates (taken together with adjacent intervals
$(s,\phi )$
-coordinates (taken together with adjacent intervals
![]() $J_i$
). The latter statement follows from [Reference Glutsyuk10, Lemma 3.1] applied to the second component of the diffeomorphism H.
$J_i$
). The latter statement follows from [Reference Glutsyuk10, Lemma 3.1] applied to the second component of the diffeomorphism H.
The results stated below on conjugacy of billiard maps near the boundary are corollaries of Theorems 1.27 and 1.30 on normal forms of
![]() $C^\infty $
-lifted strongly billiard-like maps and their liftings.
$C^\infty $
-lifted strongly billiard-like maps and their liftings.
Theorem 1.39. Let
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\gamma _2$
be strictly convex
$\gamma _2$
be strictly convex
![]() $C^\infty $
-smooth one-dimensional submanifolds in
$C^\infty $
-smooth one-dimensional submanifolds in
![]() ${\mathbb R}^2$
parameterized by intervals (thus, going to infinity in both directions) and positively oriented as boundaries of their convex sides. Let, in addition, the curves
${\mathbb R}^2$
parameterized by intervals (thus, going to infinity in both directions) and positively oriented as boundaries of their convex sides. Let, in addition, the curves
![]() $\gamma _i$
have finite asymptotic tangent lines at infinity: as
$\gamma _i$
have finite asymptotic tangent lines at infinity: as
![]() $x\in \gamma _i$
tends to infinity (in each direction), the tangent line
$x\in \gamma _i$
tends to infinity (in each direction), the tangent line
![]() $T_x\gamma _i$
converges to a finite line. Then the corresponding billiard maps are
$T_x\gamma _i$
converges to a finite line. Then the corresponding billiard maps are
![]() $C^\infty $
-smoothly conjugated near the boundary in
$C^\infty $
-smoothly conjugated near the boundary in
![]() $(s,y)$
- (and hence, in
$(s,y)$
- (and hence, in
![]() $(s,\phi $
)-) coordinates.
$(s,\phi $
)-) coordinates.
Theorem 1.40. The statement of Theorem 1.39 on conjugacy of billiard maps corresponding to
![]() $C^\infty $
-smooth strictly convex curves
$C^\infty $
-smooth strictly convex curves
![]() $\gamma _i$
remains valid in the case when each
$\gamma _i$
remains valid in the case when each
![]() $\gamma _j$
is either a submanifold going to infinity in both directions or a (may be immersed) subarc of an (immersed)
$\gamma _j$
is either a submanifold going to infinity in both directions or a (may be immersed) subarc of an (immersed)
![]() $C^\infty $
-smooth curve, and the two following statements hold:
$C^\infty $
-smooth curve, and the two following statements hold:
-
(1) as the length parameter s of the curve
 $\gamma _j$
goes to an endpoint of the length parameter interval, the corresponding point of the curve
$\gamma _j$
goes to an endpoint of the length parameter interval, the corresponding point of the curve
 $\gamma _j$
tends either to a finite limit (endpoint of
$\gamma _j$
tends either to a finite limit (endpoint of
 $\gamma _j$
) where
$\gamma _j$
) where
 $\gamma _j$
is
$\gamma _j$
is
 $C^2$
-smooth, or to infinity;
$C^2$
-smooth, or to infinity; -
(2) in the latter case, when the limit is infinite, the tangent line
 $T_s\gamma _j$
has a finite limit: a finite asymptotic tangent line.
$T_s\gamma _j$
has a finite limit: a finite asymptotic tangent line.
Remark 1.41. Kaloshin and Koudjinan [Reference Kaloshin and Koudjinan12] proved continuous conjugacy near the boundary of two billiard maps corresponding to two arbitrary ellipses. For any two ellipses with two appropriate points deleted in each of them, they have also proved smooth conjugacy of the corresponding billiard maps on open domains adjacent to the corresponding boundary intervals J in the
![]() $(s,\phi )$
-coordinates.
$(s,\phi )$
-coordinates.
Below we state a more general result and provide a sufficient condition of symplectic conjugacy of billiard maps in the coordinates
![]() $(s,y)$
. To this end, let us recall the following definition.
$(s,y)$
. To this end, let us recall the following definition.
Definition 1.42. Let
![]() $\gamma $
be a
$\gamma $
be a
![]() $C^2$
-smooth oriented planar curve, and let s be its length parameter defining its orientation. Let
$C^2$
-smooth oriented planar curve, and let s be its length parameter defining its orientation. Let
![]() $J_\gamma =(a_\gamma ,b_\gamma )\subset {\mathbb R}_s$
denote the length parameter interval parameterizing
$J_\gamma =(a_\gamma ,b_\gamma )\subset {\mathbb R}_s$
denote the length parameter interval parameterizing
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\kappa =\kappa (s)$
denote the geodesic curvature of the curve
$\kappa =\kappa (s)$
denote the geodesic curvature of the curve
![]() $\gamma $
as a function of s. The Lazutkin length of the curve
$\gamma $
as a function of s. The Lazutkin length of the curve
![]() $\gamma $
is the integral
$\gamma $
is the integral
 $$ \begin{align}{\mathcal L}(\gamma):=\int_{a_\gamma}^{b_\gamma}\kappa^{2/3}(s)\,ds,\end{align} $$
$$ \begin{align}{\mathcal L}(\gamma):=\int_{a_\gamma}^{b_\gamma}\kappa^{2/3}(s)\,ds,\end{align} $$
see [Reference Lazutkin15, equation (1.3)]. (While the length parameter interval is defined up to translation, the integral
![]() ${\mathcal L}(\gamma )$
is uniquely defined.)
${\mathcal L}(\gamma )$
is uniquely defined.)
Theorem 1.43. Let
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\gamma _2$
be two strictly convex
$\gamma _2$
be two strictly convex
![]() $C^\infty $
-smooth (may be immersed) planar curves, parameterized by intervals and positively oriented as local boundaries of their convex sides. The corresponding billiard maps are
$C^\infty $
-smooth (may be immersed) planar curves, parameterized by intervals and positively oriented as local boundaries of their convex sides. The corresponding billiard maps are
![]() $C^\infty $
-smoothly conjugated near the boundary in
$C^\infty $
-smoothly conjugated near the boundary in
![]() $(s,y)$
-coordinates, if and only if one of the two following conditions holds:
$(s,y)$
-coordinates, if and only if one of the two following conditions holds:
-
(i) either both Lazutkin lengths
 ${\mathcal L}(\gamma _i)$
are finite;
${\mathcal L}(\gamma _i)$
are finite; -
(ii) or both Lazutkin lengths
 ${\mathcal L}(\gamma _i)$
are infinite and the improper integrals in equation (1.19) defining them are
${\mathcal L}(\gamma _i)$
are infinite and the improper integrals in equation (1.19) defining them are-
(a) either both infinite in both directions;
-
(b) or both infinite in one and the same direction (with respect to the orientations of the curves
 $\gamma _i$
) and both finite in the other direction.
$\gamma _i$
) and both finite in the other direction.
-
The same criterion also holds for
![]() $C^\infty $
-smooth conjugacy near the boundary in
$C^\infty $
-smooth conjugacy near the boundary in
![]() $(s,\phi )$
-coordinates.
$(s,\phi )$
-coordinates.
Theorem 1.44. Let in the conditions of Theorem 1.43 some of conditions (i) or (ii) hold. Then the billiard maps are
![]() $C^\infty $
-smoothly symplectically conjugated near the boundary if and only if the Lazutkin lengths of the curves
$C^\infty $
-smoothly symplectically conjugated near the boundary if and only if the Lazutkin lengths of the curves
![]() $\gamma _j$
are either both finite and equal, or both infinite and the above condition (ii) holds.
$\gamma _j$
are either both finite and equal, or both infinite and the above condition (ii) holds.
Theorems 1.39 and 1.40 will be deduced from Theorem 1.43 using the following propositions on
![]() $C^\infty $
-lifted strongly billiard-like maps and lemma on curves with asymptotic line at infinity.
$C^\infty $
-lifted strongly billiard-like maps and lemma on curves with asymptotic line at infinity.
Proposition 1.45. Let
![]() $F(s,y)=(s+w(s)\sqrt y+O(y),y+O(y^{3/2}))$
be a
$F(s,y)=(s+w(s)\sqrt y+O(y),y+O(y^{3/2}))$
be a
![]() $C^\infty $
-lifted strongly billiard-like map, see equation (1.7), defined on
$C^\infty $
-lifted strongly billiard-like map, see equation (1.7), defined on
![]() $U\cup J$
, where
$U\cup J$
, where
![]() $J=(a,b)\times \{0\}$
and
$J=(a,b)\times \{0\}$
and
![]() $U\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J. Let
$U\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J. Let
![]() $H(s,y)=(H_1(s,y),H_2(s,y))$
be a
$H(s,y)=(H_1(s,y),H_2(s,y))$
be a
![]() $C^\infty $
-smooth diffeomorphism of the domain with boundary
$C^\infty $
-smooth diffeomorphism of the domain with boundary
![]() $U\cup J$
onto its image in
$U\cup J$
onto its image in
![]() ${\mathbb R}\times {\mathbb R}_{\geq 0}$
that conjugates F with its normal form
${\mathbb R}\times {\mathbb R}_{\geq 0}$
that conjugates F with its normal form
![]() ${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
, that is,
${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
, that is,
![]() ${H\circ F\circ H^{-1}={\Lambda } }$
. Fix a
${H\circ F\circ H^{-1}={\Lambda } }$
. Fix a
![]() $s_0\in (a,b)$
.
$s_0\in (a,b)$
.
-
(1) The diffeomorphism H is orientation-preserving,
 $H(J)\subset {\mathbb R}\times \{0\}$
, and the restriction
$H(J)\subset {\mathbb R}\times \{0\}$
, and the restriction
 $H_1(s,0)$
to J of its first component is an increasing function.
$H_1(s,0)$
to J of its first component is an increasing function. -
(2) If H is symplectic, then, up to additive constant,
(1.20) $$ \begin{align} H_1(s,0)=t_L(s):=\int_{s_0}^sw^{-(2/3)}(s)\,ds. \end{align} $$
$$ \begin{align} H_1(s,0)=t_L(s):=\int_{s_0}^sw^{-(2/3)}(s)\,ds. \end{align} $$
-
(3) If H is not necessarily symplectic, then
(1.21) $$ \begin{align} H_1(s,0)=\alpha t_L(s)+\beta \quad\text{for some } \alpha>0 \quad\text{and}\quad\beta\in{\mathbb R}.\end{align} $$
$$ \begin{align} H_1(s,0)=\alpha t_L(s)+\beta \quad\text{for some } \alpha>0 \quad\text{and}\quad\beta\in{\mathbb R}.\end{align} $$
Proposition 1.46. Let F, U, J be the same, as in Proposition 1.45. Let
![]() $\widetilde {F}$
be the lifting of the map F to the coordinates
$\widetilde {F}$
be the lifting of the map F to the coordinates
![]() $(s,\psi )$
,
$(s,\psi )$
,
![]() $\psi ^2=y$
, which is a
$\psi ^2=y$
, which is a
![]() $C^\infty $
-smooth diffeomorphism defined on
$C^\infty $
-smooth diffeomorphism defined on
![]() $\widetilde {U}\cup J$
,
$\widetilde {U}\cup J$
,
![]() $\widetilde {U}=\{(s,\psi ) \mid (s,\psi ^2)\in U, \ \psi>0\}$
. Let
$\widetilde {U}=\{(s,\psi ) \mid (s,\psi ^2)\in U, \ \psi>0\}$
. Let
![]() $\widetilde {H}$
be a
$\widetilde {H}$
be a
![]() $C^\infty $
-smooth diffeomorphism defined on
$C^\infty $
-smooth diffeomorphism defined on
![]() $\widetilde {U}\cup J$
conjugating
$\widetilde {U}\cup J$
conjugating
![]() $\widetilde {F}$
with the diffeomorphism
$\widetilde {F}$
with the diffeomorphism
![]() $\widetilde {\Lambda } :(t,\widetilde {z})\mapsto (t+\widetilde {z},\widetilde {z})$
:
$\widetilde {\Lambda } :(t,\widetilde {z})\mapsto (t+\widetilde {z},\widetilde {z})$
:
![]() $\widetilde {H}\circ \widetilde {F}\circ \widetilde {H}^{-1}=\widetilde {\Lambda } $
. Then
$\widetilde {H}\circ \widetilde {F}\circ \widetilde {H}^{-1}=\widetilde {\Lambda } $
. Then
![]() $\widetilde {H}(J)\subset {\mathbb R}\times \{0\}$
, and the first component of the map
$\widetilde {H}(J)\subset {\mathbb R}\times \{0\}$
, and the first component of the map
![]() $\widetilde {H}$
satisfies equation (1.21).
$\widetilde {H}$
satisfies equation (1.21).
Lemma 1.47. Let a
![]() $C^\infty $
-smooth strictly convex planar curve
$C^\infty $
-smooth strictly convex planar curve
![]() $\gamma $
go to infinity in some direction, and let it have a finite asymptotic tangent line at infinity in this direction (in the same sense as in Theorem 1.39). Then the improper integral in equation (1.19) defining the Lazutkin length converges in the given direction.
$\gamma $
go to infinity in some direction, and let it have a finite asymptotic tangent line at infinity in this direction (in the same sense as in Theorem 1.39). Then the improper integral in equation (1.19) defining the Lazutkin length converges in the given direction.
Remark 1.48. For a
![]() $C^\infty $
-smooth strictly convex planar curve going to infinity, the existence of a finite asymptotic tangent line is not a necessary condition for convergence of the improper integral in equation (1.19) defining the Lazutkin length. Namely, consider the graph
$C^\infty $
-smooth strictly convex planar curve going to infinity, the existence of a finite asymptotic tangent line is not a necessary condition for convergence of the improper integral in equation (1.19) defining the Lazutkin length. Namely, consider the graph
![]() $\{ y=x^r\}\subset [1,+\infty )\times [1,+\infty )$
,
$\{ y=x^r\}\subset [1,+\infty )\times [1,+\infty )$
,
![]() $r>1$
. One has
$r>1$
. One has
Indeed,
![]() $ds=\sqrt {1+r^2x^{2(r-1)}}\,dx$
,
$ds=\sqrt {1+r^2x^{2(r-1)}}\,dx$
,
![]() $\kappa (s(x))= {r(r-1)x^{r-2}}/{(1+r^2x^{2(r-1)})^{3/2}}$
, see equation (2.59),
$\kappa (s(x))= {r(r-1)x^{r-2}}/{(1+r^2x^{2(r-1)})^{3/2}}$
, see equation (2.59),
 $$ \begin{align*} \kappa^{2/3}(s(x))\,ds=(r(r-1))^{2/3} \frac{x^{(2/3)(r-2)}}{\sqrt{1+r^2x^{2(r-1)}}}\,dx\simeq(r(r-1))^{2/3}x^\nu \,dx,\!\quad \nu=-\frac{r+1}3, \end{align*} $$
$$ \begin{align*} \kappa^{2/3}(s(x))\,ds=(r(r-1))^{2/3} \frac{x^{(2/3)(r-2)}}{\sqrt{1+r^2x^{2(r-1)}}}\,dx\simeq(r(r-1))^{2/3}x^\nu \,dx,\!\quad \nu=-\frac{r+1}3, \end{align*} $$
as
![]() $x\to +\infty $
. Therefore, the integral in equation (1.22) converges if and only if
$x\to +\infty $
. Therefore, the integral in equation (1.22) converges if and only if
![]() $\nu <-1$
, that is,
$\nu <-1$
, that is,
![]() $r>2$
. In the case of parabola
$r>2$
. In the case of parabola
![]() $\{ y=x^2\}$
, the integral in equation (1.22) diverges.
$\{ y=x^2\}$
, the integral in equation (1.22) diverges.
1.7 Plan of the proof of main results
In §2.1, we recall the above-mentioned result of Marvizi and Melrose [Reference Marvizi and Melrose16, Theorem 3.2] (with proof) yielding
![]() $C^{\infty }$
-smooth coordinates in which a
$C^{\infty }$
-smooth coordinates in which a
![]() $C^\infty $
-lifted strongly billiard-like map F takes the form
$C^\infty $
-lifted strongly billiard-like map F takes the form
![]() $F(\tau ,h)=(\tau +\sqrt h+{\operatorname {flat}}(h), h+{\operatorname {flat}}(h))$
. It implies that the lifted map
$F(\tau ,h)=(\tau +\sqrt h+{\operatorname {flat}}(h), h+{\operatorname {flat}}(h))$
. It implies that the lifted map
![]() $\widetilde {F}$
, written in the coordinates
$\widetilde {F}$
, written in the coordinates
![]() $(\tau ,\phi )$
,
$(\tau ,\phi )$
,
![]() $\phi =\sqrt h$
, takes form of equation (1.13).
$\phi =\sqrt h$
, takes form of equation (1.13).
Statement (1) of Theorem 1.30 will be proved in §§2.2–2.4. To do this, first in §2.2, we construct a fundamental domain for the map
![]() $\widetilde {F}$
(a curvilinear sector
$\widetilde {F}$
(a curvilinear sector
![]() $\Delta $
with vertex at a point in J) and an
$\Delta $
with vertex at a point in J) and an
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
![]() $\widetilde {\phi }$
defined on a bigger sector that is
$\widetilde {\phi }$
defined on a bigger sector that is
![]() $\phi $
-flatly close to
$\phi $
-flatly close to
![]() $\phi $
on the latter bigger sector. Then in §2.3, we construct its
$\phi $
on the latter bigger sector. Then in §2.3, we construct its
![]() $\widetilde {F}$
-invariant extension along the
$\widetilde {F}$
-invariant extension along the
![]() $\widetilde {F}$
-orbits and show that it is well defined on a domain adjacent to J. In §2.4, we prove that the extended function
$\widetilde {F}$
-orbits and show that it is well defined on a domain adjacent to J. In §2.4, we prove that the extended function
![]() $\widetilde {\phi }$
is
$\widetilde {\phi }$
is
![]() $C^{\infty }$
-smooth and
$C^{\infty }$
-smooth and
![]() $\phi $
-flatly close to
$\phi $
-flatly close to
![]() $\phi $
. This will prove statement (1) of Theorem 1.30. Statement (2) on normal form will be proved in §2.5.
$\phi $
. This will prove statement (1) of Theorem 1.30. Statement (2) on normal form will be proved in §2.5.
The existence statement in Theorem 1.26 will be deduced from statement (1) of Theorem 1.30 in §2.6, where we will also prove Theorem 1.27. Existence in Theorems 1.9, 1.12, and 1.13 will be proved in §2.7. The results from §1.5 on jets and space of germs of foliations will be proved in §2.8. Proposition 1.36 and non-uniqueness statements in the main theorems will be proved in §2.9.
The results of §1.6 on conjugacy of billiard maps near the boundary will be proved in §2.10.
2 Construction of foliation by invariant curves. Proofs of main results
2.1 Marvizi and Melrose construction of an ‘up-to-flat’ first integral
Here we recall the following theorem of Marvizi and Melrose with proof. Though it was stated in [Reference Marvizi and Melrose16] for billiard ball maps, its statement and proof remain valid for
![]() $C^\infty $
-lifted strongly billiard-like maps.
$C^\infty $
-lifted strongly billiard-like maps.
Theorem 2.1. [Reference Marvizi and Melrose16, Theorem 3.2]
-
(1) Let
 $V{\kern-1pt}\subset{\kern-1pt} (a,b)\times {\mathbb R}_{>0}{\kern-1pt}\subset{\kern-1pt} {\mathbb R}^2_{s,y}$
be a domain adjacent to the interval
$V{\kern-1pt}\subset{\kern-1pt} (a,b)\times {\mathbb R}_{>0}{\kern-1pt}\subset{\kern-1pt} {\mathbb R}^2_{s,y}$
be a domain adjacent to the interval
 $J{\kern-1pt}:={\kern-1pt}(a,b){\kern-1pt}\times \{0\}$
. Let
$J{\kern-1pt}:={\kern-1pt}(a,b){\kern-1pt}\times \{0\}$
. Let
 $F:V\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a
$F:V\cup J\to {\mathbb R}\times {\mathbb R}_{\geq 0}$
be a
 $C^{\infty }$
-lifted strongly billiard-like map. There exists a domain
$C^{\infty }$
-lifted strongly billiard-like map. There exists a domain
 $W\subset V$
adjacent to J and a real-valued
$W\subset V$
adjacent to J and a real-valued
 $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
 $h:W\cup J\to {\mathbb R}_{\geq 0}$
,
$h:W\cup J\to {\mathbb R}_{\geq 0}$
,
 $h|_J\equiv 0$
,
$h|_J\equiv 0$
,
 $({\partial h}/{\partial y})|_J>0$
, such that the difference
$({\partial h}/{\partial y})|_J>0$
, such that the difference
 $h\circ F-h$
is
$h\circ F-h$
is
 $C^{\infty }$
-smooth and y-flat. Moreover, one can normalize h as above so that the mapping F coincides, up to y-flat terms, with the time-1 map of the flow of the Hamiltonian vector field with the Hamiltonian function
$C^{\infty }$
-smooth and y-flat. Moreover, one can normalize h as above so that the mapping F coincides, up to y-flat terms, with the time-1 map of the flow of the Hamiltonian vector field with the Hamiltonian function
 $\tfrac 23 h^{3/2}$
. This normalization determines the asymptotic Taylor series
$\tfrac 23 h^{3/2}$
. This normalization determines the asymptotic Taylor series
 $h(s,y)=\sum _{k=1}^{+\infty }h_k(s)y^k$
of the function
$h(s,y)=\sum _{k=1}^{+\infty }h_k(s)y^k$
of the function
 $h(s,y)$
uniquely.
$h(s,y)$
uniquely. -
(2) The analogue of the above statement holds if J is replaced by the coordinate circle
 $S^1=S^1\times \{0\}$
,
$S^1=S^1\times \{0\}$
,
 $S^1:={\mathbb R}_s / {\mathbb Z}$
, lying in the cylinder
$S^1:={\mathbb R}_s / {\mathbb Z}$
, lying in the cylinder
 $C:=S^1\times [0,{\varepsilon } )$
equipped with the standard area form and F is a strongly billiard-like map
$C:=S^1\times [0,{\varepsilon } )$
equipped with the standard area form and F is a strongly billiard-like map
 $C\to S^1\times {\mathbb R}_{\geq 0}$
. In this case, the coefficients
$C\to S^1\times {\mathbb R}_{\geq 0}$
. In this case, the coefficients
 $h_k(s)$
of the above normalized series are 1-periodic and
$h_k(s)$
of the above normalized series are 1-periodic and
 $C^{\infty }$
-smooth.
$C^{\infty }$
-smooth. -
(3) Let h be the function normalized as in statement (1). Let
 $\tau $
denote the time function for the Hamiltonian vector field with the Hamiltonian function h. In the coordinates
$\tau $
denote the time function for the Hamiltonian vector field with the Hamiltonian function h. In the coordinates
 $(\tau ,h)$
(which are symplectic), the map F takes the form (2.1)
$(\tau ,h)$
(which are symplectic), the map F takes the form (2.1) $$ \begin{align} F:(\tau,h)\mapsto(\tau+\sqrt h+{\operatorname{flat}}(h), h+{\operatorname{flat}}(h)). \end{align} $$
$$ \begin{align} F:(\tau,h)\mapsto(\tau+\sqrt h+{\operatorname{flat}}(h), h+{\operatorname{flat}}(h)). \end{align} $$
Proof. The lifting
![]() $\widetilde {F}(s,z)$
,
$\widetilde {F}(s,z)$
,
![]() $z=\sqrt y$
, of the map
$z=\sqrt y$
, of the map
![]() $F(s,y)$
is
$F(s,y)$
is
![]() $C^{\infty }$
-smooth and has the form
$C^{\infty }$
-smooth and has the form
 $$ \begin{align} \widetilde{F}(s,z)=\bigg(s+w(s)z+O(z^2), z+\frac{q(s)}2z^2+O(z^3)\bigg), \end{align} $$
$$ \begin{align} \widetilde{F}(s,z)=\bigg(s+w(s)z+O(z^2), z+\frac{q(s)}2z^2+O(z^3)\bigg), \end{align} $$
where
![]() $q(s)$
is a
$q(s)$
is a
![]() $C^{\infty }$
-smooth function on
$C^{\infty }$
-smooth function on
![]() $(a,b)$
. This follows from equation (1.7) and
$(a,b)$
. This follows from equation (1.7) and
![]() $C^\infty $
-liftedness. The map
$C^\infty $
-liftedness. The map
![]() $\widetilde {F}(s,z)$
admits an asymptotic Taylor series in z. The map F has the form
$\widetilde {F}(s,z)$
admits an asymptotic Taylor series in z. The map F has the form
by equation (2.2), and it admits an asymptotic Puiseux series in y involving powers
![]() $0, \tfrac 12, 1, \tfrac 32, 2,\ldots .$
The coefficients of both series are
$0, \tfrac 12, 1, \tfrac 32, 2,\ldots .$
The coefficients of both series are
![]() $C^{\infty }$
-smooth functions in s. Therefore, the mapping F acts by the formula
$C^{\infty }$
-smooth functions in s. Therefore, the mapping F acts by the formula
![]() $h\mapsto h\circ F$
not only on functions, but also on formal Puiseux series. It transforms each power series
$h\mapsto h\circ F$
not only on functions, but also on formal Puiseux series. It transforms each power series
![]() $h=\sum _{k=1}^{+\infty }h_k(s)y^k$
with coefficients being
$h=\sum _{k=1}^{+\infty }h_k(s)y^k$
with coefficients being
![]() $C^{\infty }$
-smooth functions on
$C^{\infty }$
-smooth functions on
![]() $(a,b)$
to a Puiseux series of the above type. Our goal is to find an F-invariant power series (or equivalently, an
$(a,b)$
to a Puiseux series of the above type. Our goal is to find an F-invariant power series (or equivalently, an
![]() $\widetilde {F}$
-invariant even power series
$\widetilde {F}$
-invariant even power series
![]() $\sum _{k=1}^{+\infty }h_k(s)z^{2k}$
) and then to choose its
$\sum _{k=1}^{+\infty }h_k(s)z^{2k}$
) and then to choose its
![]() $C^{\infty }$
-smooth representative. To do this, we use the following formula for the function
$C^{\infty }$
-smooth representative. To do this, we use the following formula for the function
![]() $q(s)$
in equation (2.3), see [Reference Lazutkin15, equation (1.2)], [Reference Glutsyuk10, equation (7.18)], which follows from the area-preserving property:
$q(s)$
in equation (2.3), see [Reference Lazutkin15, equation (1.2)], [Reference Glutsyuk10, equation (7.18)], which follows from the area-preserving property:
Step 1. Constructing an even series
![]() $\sum _{k=1}^{+\infty }g_k(s)z^{2k}$
whose
$\sum _{k=1}^{+\infty }g_k(s)z^{2k}$
whose
![]() $\widetilde {F}$
-image is also an even series. We construct its coefficients
$\widetilde {F}$
-image is also an even series. We construct its coefficients
![]() $g_k$
by induction as follows.
$g_k$
by induction as follows.
Induction base:
![]() $k=1$
. Let us find a function
$k=1$
. Let us find a function
![]() $g_1(s)$
such that the
$g_1(s)$
such that the
![]() $\widetilde {F}$
-image of the function
$\widetilde {F}$
-image of the function
![]() $g_1(s)z^2$
contains no
$g_1(s)z^2$
contains no
![]() $z^3$
-term. This is equivalent to the statement saying that the function
$z^3$
-term. This is equivalent to the statement saying that the function
![]() $g_1(s+w(s)z)(z+ ({q(s)}/2)z^2)^2$
contains no
$g_1(s+w(s)z)(z+ ({q(s)}/2)z^2)^2$
contains no
![]() $z^3$
-term, which is, in its turn, equivalent to the differential equation
$z^3$
-term, which is, in its turn, equivalent to the differential equation
which has a unique solution
![]() $g_1(s)=w^{2/3}(s)$
up to constant factor. (Note that
$g_1(s)=w^{2/3}(s)$
up to constant factor. (Note that
![]() $w^{2/3}(s)y$
is a well-known function: the second Lazutkin coordinate [Reference Lazutkin15, Reference Marvizi and Melrose16].)
$w^{2/3}(s)y$
is a well-known function: the second Lazutkin coordinate [Reference Lazutkin15, Reference Marvizi and Melrose16].)
Induction step in the case when
![]() $J=(a,b)\times \{0\}$
is an interval. We have already found an even Taylor polynomial
$J=(a,b)\times \{0\}$
is an interval. We have already found an even Taylor polynomial
![]() $G_{n-1}(s,z):=\sum _{k=1}^{n-1}g_k(s)z^{2k}$
,
$G_{n-1}(s,z):=\sum _{k=1}^{n-1}g_k(s)z^{2k}$
,
![]() $n\geq 2$
, such that the asymptotic Taylor series in z of the function
$n\geq 2$
, such that the asymptotic Taylor series in z of the function
![]() $G_{n-1}\circ \widetilde {F}$
contains no odd powers of z of degrees no greater than
$G_{n-1}\circ \widetilde {F}$
contains no odd powers of z of degrees no greater than
![]() $2n-1$
. Let us construct
$2n-1$
. Let us construct
![]() $g_{n}(s)$
and set
$g_{n}(s)$
and set
![]() $G_n(s,z):=\sum _{k=1}^{n}g_k(s)z^{2k}$
so that
$G_n(s,z):=\sum _{k=1}^{n}g_k(s)z^{2k}$
so that
Note that
![]() $G_n\circ \widetilde {F}-G_n$
obviously cannot contain odd powers of degrees less than
$G_n\circ \widetilde {F}-G_n$
obviously cannot contain odd powers of degrees less than
![]() $2n$
. Let
$2n$
. Let
![]() $b(s)z^{2n+1}$
denote the degree
$b(s)z^{2n+1}$
denote the degree
![]() $2n+1$
term in the Taylor series of the function
$2n+1$
term in the Taylor series of the function
![]() $G_{n-1}\circ \widetilde {F}$
. Equation (2.5) is equivalent to the differential equation
$G_{n-1}\circ \widetilde {F}$
. Equation (2.5) is equivalent to the differential equation
which always has a solution
![]() $g_n(s)$
well defined on the interval
$g_n(s)$
well defined on the interval
![]() $(a,b)$
.
$(a,b)$
.
Step 2. Constructing an
![]() $\widetilde {F}$
-invariant series. The mapping
$\widetilde {F}$
-invariant series. The mapping
![]() $\widetilde {F}$
is the product
$\widetilde {F}$
is the product
![]() $I\circ \beta $
of two involutions:
$I\circ \beta $
of two involutions:
![]() $I(s,z)=(s,-z)$
and
$I(s,z)=(s,-z)$
and
![]() $\beta $
. Let
$\beta $
. Let
![]() $g:=\sum _{k=1}^{+\infty }g_k(s)z^{2k}$
be the series constructed in Step 1. One has
$g:=\sum _{k=1}^{+\infty }g_k(s)z^{2k}$
be the series constructed in Step 1. One has
since the series g is even. The series in equation (2.7) is even (Step 1). Hence, the series
is even and
![]() $\beta $
-invariant by construction. Therefore, it is
$\beta $
-invariant by construction. Therefore, it is
![]() $\widetilde {F}$
-invariant. Its first coefficient is equal to
$\widetilde {F}$
-invariant. Its first coefficient is equal to
![]() $2g_1(s)=2w^{2/3}(s)>0$
, by construction. We denote the
$2g_1(s)=2w^{2/3}(s)>0$
, by construction. We denote the
![]() $\widetilde {F}$
-invariant series thus constructed by
$\widetilde {F}$
-invariant series thus constructed by
![]() $t:=\sum _{k=1}^{+\infty }t_k(s)z^{2k}$
.
$t:=\sum _{k=1}^{+\infty }t_k(s)z^{2k}$
.
Step 3. Symplectic coordinates and normalization. Let
![]() $t(s,y)$
be a function representing the series
$t(s,y)$
be a function representing the series
![]() $\sum _{k=1}^{+\infty }t_k(s)y^{k}$
, which is obtained from the latter series (given by Step 2) by the variable change
$\sum _{k=1}^{+\infty }t_k(s)y^{k}$
, which is obtained from the latter series (given by Step 2) by the variable change
![]() $y=z^2$
. It is defined on a domain W adjacent to J and
$y=z^2$
. It is defined on a domain W adjacent to J and
![]() $C^{\infty }$
-smooth on
$C^{\infty }$
-smooth on
![]() $W\cup J$
;
$W\cup J$
;
![]() $t|_J\equiv 0$
,
$t|_J\equiv 0$
,
![]() $({\partial t}/{\partial y})|_J>0$
. Let
$({\partial t}/{\partial y})|_J>0$
. Let
![]() $H_t$
denote the corresponding Hamiltonian vector field. Fix an arbitrary
$H_t$
denote the corresponding Hamiltonian vector field. Fix an arbitrary
![]() $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
![]() $\theta $
such that
$\theta $
such that
![]() $d\theta (H_t)\equiv 1$
,
$d\theta (H_t)\equiv 1$
,
![]() $\theta |_{s=0}=0$
: a time function for the vector field
$\theta |_{s=0}=0$
: a time function for the vector field
![]() $H_t$
. Then
$H_t$
. Then
![]() $(\theta ,t)$
are symplectic coordinates for the form
$(\theta ,t)$
are symplectic coordinates for the form
![]() $\omega =dx\wedge \,dy$
:
$\omega =dx\wedge \,dy$
:
![]() $\omega =d\theta \wedge \,dt$
. Shrinking W (keeping it adjacent to J), we can and will consider that they are global coordinates on
$\omega =d\theta \wedge \,dt$
. Shrinking W (keeping it adjacent to J), we can and will consider that they are global coordinates on
![]() $W\cup J$
. The difference
$W\cup J$
. The difference
![]() $t\circ F-t$
is t-flat, by construction, and hence, so is
$t\circ F-t$
is t-flat, by construction, and hence, so is
![]() $dF(H_t)-H_t$
. Therefore, in the coordinates
$dF(H_t)-H_t$
. Therefore, in the coordinates
![]() $(\theta ,t)$
, the symplectic map F takes the form
$(\theta ,t)$
, the symplectic map F takes the form
In the new coordinates
![]() $(\theta ,t)$
, the map F is
$(\theta ,t)$
, the map F is
![]() $C^{\infty }$
-lifted strongly billiard-like, as in the old coordinates
$C^{\infty }$
-lifted strongly billiard-like, as in the old coordinates
![]() $(s,y)$
, by Proposition 1.24.
$(s,y)$
, by Proposition 1.24.
Claim 1. The function
![]() $\xi (t)$
in equation (2.8) has the form
$\xi (t)$
in equation (2.8) has the form
![]() $\xi (t)=\sqrt t \psi (t)$
, where
$\xi (t)=\sqrt t \psi (t)$
, where
![]() $\psi (t)$
is a
$\psi (t)$
is a
![]() $C^{\infty }$
-smooth function on a segment
$C^{\infty }$
-smooth function on a segment
![]() $[0,{\varepsilon } ]$
,
$[0,{\varepsilon } ]$
,
![]() ${\varepsilon }>0$
,
${\varepsilon }>0$
,
![]() $\psi \geq 0$
,
$\psi \geq 0$
,
![]() $\psi (0)>0$
.
$\psi (0)>0$
.
Proof. Let
![]() $\widetilde {F}$
denote the lifting of the map F to the coordinates
$\widetilde {F}$
denote the lifting of the map F to the coordinates
![]() $(\theta ,\zeta )$
,
$(\theta ,\zeta )$
,
![]() $\zeta =\sqrt t$
. One has
$\zeta =\sqrt t$
. One has
![]() $\widetilde {F}=I\circ \beta $
, where
$\widetilde {F}=I\circ \beta $
, where
![]() $I(\theta ,\zeta )=(\theta ,-\zeta )$
and
$I(\theta ,\zeta )=(\theta ,-\zeta )$
and
![]() $\beta $
is an involution,
$\beta $
is an involution,
![]() $\beta (\theta ,0)\equiv (\theta ,0)$
. The involution
$\beta (\theta ,0)\equiv (\theta ,0)$
. The involution
![]() $\beta $
takes the form
$\beta $
takes the form
The function
![]() $r(\zeta )$
should be
$r(\zeta )$
should be
![]() $C^{\infty }$
-smooth, as is
$C^{\infty }$
-smooth, as is
![]() $\beta $
, and
$\beta $
, and
![]() $r'(0)>0$
(strong billiard-likedness). The condition saying that
$r'(0)>0$
(strong billiard-likedness). The condition saying that
![]() $\beta $
is an involution implies that
$\beta $
is an involution implies that
![]() $r(\zeta )+r(-\zeta )={\operatorname {flat}}(\zeta )$
. This, in its turn, implies that
$r(\zeta )+r(-\zeta )={\operatorname {flat}}(\zeta )$
. This, in its turn, implies that
![]() $r(\zeta )=\zeta \psi (\zeta ^2)+{\operatorname {flat}}(\zeta )$
, where
$r(\zeta )=\zeta \psi (\zeta ^2)+{\operatorname {flat}}(\zeta )$
, where
![]() $\psi $
is a
$\psi $
is a
![]() $C^{\infty }$
-smooth function;
$C^{\infty }$
-smooth function;
![]() $\psi (0)=r'(0)>0$
. This together with equation (2.9) implies the statement of the claim.
$\psi (0)=r'(0)>0$
. This together with equation (2.9) implies the statement of the claim.
We have to find a function
![]() $h(s,y)$
,
$h(s,y)$
,
![]() $h(s,0)\equiv 0$
, such that the Hamiltonian vector field with the Hamiltonian function
$h(s,0)\equiv 0$
, such that the Hamiltonian vector field with the Hamiltonian function
![]() $\tfrac 23 h^{3/2}$
coincides with
$\tfrac 23 h^{3/2}$
coincides with
![]() $\xi (t) {\partial }/{\partial \theta }$
. This function will satisfy the normalization statement of Theorem 2.1, part (1), by construction. We are looking for it as a function depending only on t:
$\xi (t) {\partial }/{\partial \theta }$
. This function will satisfy the normalization statement of Theorem 2.1, part (1), by construction. We are looking for it as a function depending only on t:
![]() $h(s,y)=v(t)$
. The above Hamiltonian vector field is then equal to
$h(s,y)=v(t)$
. The above Hamiltonian vector field is then equal to
![]() $\sqrt {v(t)}v'(t){\partial }/{\partial \theta }$
. Thus, we have to solve the equation
$\sqrt {v(t)}v'(t){\partial }/{\partial \theta }$
. Thus, we have to solve the equation
Its solution
![]() $v(t)$
is given by
$v(t)$
is given by
 $$ \begin{align*} v(t)=\bigg(\frac32\int_0^t\sqrt p\psi(p)\,dp\bigg)^{2/3}. \end{align*} $$
$$ \begin{align*} v(t)=\bigg(\frac32\int_0^t\sqrt p\psi(p)\,dp\bigg)^{2/3}. \end{align*} $$
This is a
![]() $C^{\infty }$
-smooth function, by construction and smoothness of the function
$C^{\infty }$
-smooth function, by construction and smoothness of the function
![]() $\psi (t)$
. One has
$\psi (t)$
. One has
![]() $({\partial h}/{\partial y})|_J>0$
, since
$({\partial h}/{\partial y})|_J>0$
, since
![]() $v'(0)=\psi ^{2/3}(0)>0$
and
$v'(0)=\psi ^{2/3}(0)>0$
and
![]() ${\partial t}/{\partial y}(s,0)=2g_1(s)= 2w^{2/3}(s)>0$
, by construction. Uniqueness of the Taylor series in y of the function
${\partial t}/{\partial y}(s,0)=2g_1(s)= 2w^{2/3}(s)>0$
, by construction. Uniqueness of the Taylor series in y of the function
![]() $h(s,y)$
satisfying the above Hamiltonian vector field statement (up to flat terms) follows directly, as in [Reference Marvizi and Melrose16, p. 383]. Statement (1) of Theorem 2.1 is proved. Statement (3) follows immediately from statement (1), since in the coordinates
$h(s,y)$
satisfying the above Hamiltonian vector field statement (up to flat terms) follows directly, as in [Reference Marvizi and Melrose16, p. 383]. Statement (1) of Theorem 2.1 is proved. Statement (3) follows immediately from statement (1), since in the coordinates
![]() $(\tau ,h)$
, see statement (3), the Hamiltonian field with the Hamiltonian function
$(\tau ,h)$
, see statement (3), the Hamiltonian field with the Hamiltonian function
![]() $\tfrac 23 h^{3/2}$
is equal to
$\tfrac 23 h^{3/2}$
is equal to
![]() $(\sqrt h, 0)$
. Statement (2) (in the case when J is a circle and F is defined on a cylinder bounded by J) says that the Taylor coefficients of the series in y of the function
$(\sqrt h, 0)$
. Statement (2) (in the case when J is a circle and F is defined on a cylinder bounded by J) says that the Taylor coefficients of the series in y of the function
![]() $h(s,y)$
are well-defined functions on the circle J. This follows from the above uniqueness statement (which holds locally, in a neighborhood of every point
$h(s,y)$
are well-defined functions on the circle J. This follows from the above uniqueness statement (which holds locally, in a neighborhood of every point
![]() $(s_0,0)\in J$
). Theorem 2.1 is proved.
$(s_0,0)\in J$
). Theorem 2.1 is proved.
2.2 Step 1. Construction of an invariant function on a neighborhood of fundamental domain
Here we give the first step of the proof of Theorem 1.30. We consider a fundamental sector
![]() $\Delta $
for the map
$\Delta $
for the map
![]() $\widetilde {F}$
that is bounded by the segment
$\widetilde {F}$
that is bounded by the segment
![]() $K=[0, \eta /2]$
of the
$K=[0, \eta /2]$
of the
![]() $\phi $
-axis, by its
$\phi $
-axis, by its
![]() $\widetilde {F}$
-image and by the straightline segment connecting their ends. We construct an
$\widetilde {F}$
-image and by the straightline segment connecting their ends. We construct an
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
![]() $\widetilde {\phi }$
that is
$\widetilde {\phi }$
that is
![]() $\phi $
-flatly close to
$\phi $
-flatly close to
![]() $\phi $
on a sectorial neighborhood
$\phi $
on a sectorial neighborhood
![]() $S_{\chi ,\eta }$
of
$S_{\chi ,\eta }$
of
![]() $\overline \Delta \setminus \{(0,0)\}$
. See Figure 5.
$\overline \Delta \setminus \{(0,0)\}$
. See Figure 5.

Figure 5 The fundamental domain
![]() $\Delta $
and its sectorial neighborhood
$\Delta $
and its sectorial neighborhood
![]() $S_{\chi ,\eta }$
.
$S_{\chi ,\eta }$
.
Without loss of generality, we consider that the
![]() $\tau $
-interval contains the origin:
$\tau $
-interval contains the origin:
![]() ${a<0<b}$
. Fix a number
${a<0<b}$
. Fix a number
![]() $\chi $
,
$\chi $
,
![]() $0 < \chi < \tfrac 12$
. Consider the sectors
$0 < \chi < \tfrac 12$
. Consider the sectors
The domain
![]() $S_{\chi ,\eta }$
will be the above-mentioned neighborhood of fundamental sector, where we construct an
$S_{\chi ,\eta }$
will be the above-mentioned neighborhood of fundamental sector, where we construct an
![]() $\widetilde {F}$
-invariant function.
$\widetilde {F}$
-invariant function.
Proposition 2.2. For every
![]() $\chi \in (0,\tfrac 12)$
and
$\chi \in (0,\tfrac 12)$
and
![]() $\eta>0$
small enough depending on
$\eta>0$
small enough depending on
![]() $\widetilde {F}$
and
$\widetilde {F}$
and
![]() $\chi $
, the following statements hold.
$\chi $
, the following statements hold.
-
(i) The maps
 $\widetilde {F}^{\pm 1}$
,
$\widetilde {F}^{\pm 1}$
,
 $\widetilde {F}^{\pm 2}$
are well defined on
$\widetilde {F}^{\pm 2}$
are well defined on
 $S_{\chi ,2\eta }$
.
$S_{\chi ,2\eta }$
. -
(ii) The domains
 $S_{\chi ,2\eta }$
and
$S_{\chi ,2\eta }$
and
 $\widetilde {F}^2(S_{\chi ,2\eta })$
are disjoint; the latter lies on the right from the former.
$\widetilde {F}^2(S_{\chi ,2\eta })$
are disjoint; the latter lies on the right from the former. -
(iii) The segment
 $K:=\{0\}\times [0, \eta /2]\subset {\mathbb R}^2_{\tau ,\phi }$
and its image
$K:=\{0\}\times [0, \eta /2]\subset {\mathbb R}^2_{\tau ,\phi }$
and its image
 $\widetilde {F}(K)$
intersect just by the origin;
$\widetilde {F}(K)$
intersect just by the origin;
 $\widetilde {F}(K)$
lies on the right from K. The domain
$\widetilde {F}(K)$
lies on the right from K. The domain
 $\Delta \subset S_{\chi ,2\eta }$
bounded by K,
$\Delta \subset S_{\chi ,2\eta }$
bounded by K,
 $\widetilde {F}(K)$
and the straightline segment connecting the endpoints of the arcs K and
$\widetilde {F}(K)$
and the straightline segment connecting the endpoints of the arcs K and
 $\widetilde {F}(K)$
distinct from
$\widetilde {F}(K)$
distinct from
 $(0,0)$
is a fundamental domain for the map
$(0,0)$
is a fundamental domain for the map
 $\widetilde {F}$
. See Figure 5.
$\widetilde {F}$
. See Figure 5.
Proof. One has
 $$ \begin{align} d\widetilde{F}(0,0)=\bigg(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\bigg). \end{align} $$
$$ \begin{align} d\widetilde{F}(0,0)=\bigg(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\bigg). \end{align} $$
The latter differential sends each line
![]() $\{\tau =\zeta \phi \}$
to the line
$\{\tau =\zeta \phi \}$
to the line
![]() $\{\tau =(\zeta +1)\phi \}$
. This implies that for every
$\{\tau =(\zeta +1)\phi \}$
. This implies that for every
![]() $\eta>0$
small enough, statements (i)–(iii) hold.
$\eta>0$
small enough, statements (i)–(iii) hold.
Proposition 2.3. For every
![]() $\chi \in (0,\tfrac 12)$
and
$\chi \in (0,\tfrac 12)$
and
![]() $\eta>0$
small enough depending on
$\eta>0$
small enough depending on
![]() $\widetilde {F}$
and
$\widetilde {F}$
and
![]() $\chi $
, there exists a
$\chi $
, there exists a
![]() $C^{\infty }$
-smooth and
$C^{\infty }$
-smooth and
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
![]() $\widetilde {\phi }(\tau ,\phi )$
on
$\widetilde {\phi }(\tau ,\phi )$
on
![]() $S_{\chi ,\eta }$
such that the difference
$S_{\chi ,\eta }$
such that the difference
![]() $\widetilde {\phi }(\tau ,\phi )-\phi $
is
$\widetilde {\phi }(\tau ,\phi )-\phi $
is
![]() $\phi $
-flat on
$\phi $
-flat on
![]() $S_{\chi ,\eta }$
: that is, tends to zero with all its partial derivatives, as
$S_{\chi ,\eta }$
: that is, tends to zero with all its partial derivatives, as
![]() $(\tau ,\phi )\in S_{\chi ,\eta }$
tends to zero.
$(\tau ,\phi )\in S_{\chi ,\eta }$
tends to zero.
Proof. Let
![]() $\nu :S_{\chi }\to {\mathbb R}$
denote the function
$\nu :S_{\chi }\to {\mathbb R}$
denote the function
whose level curves are lines through the origin. The interval of values of the function
![]() $\nu $
on
$\nu $
on
![]() $S_{\chi }$
is
$S_{\chi }$
is
![]() $M:=(-\chi ,1+\chi )$
. Fix a
$M:=(-\chi ,1+\chi )$
. Fix a
Consider the covering of the interval M by the intervals
and a corresponding
![]() $C^\infty $
-smooth partition of unity
$C^\infty $
-smooth partition of unity
![]() $\rho _1$
,
$\rho _1$
,
![]() $\rho _2$
:
$\rho _2$
:
![]() $M\to {\mathbb R}$
,
$M\to {\mathbb R}$
,
Set
 $$ \begin{align} \widetilde{\phi}(x)&:=\rho_1(\nu(x))\phi(x)+\rho_2(\nu(x))\phi\circ \widetilde{F}^{-1}(x) \\ &=\phi(x)+\rho_2(\nu(x))(\phi\circ\widetilde{F}^{-1}(x)-\phi(x)).\nonumber \end{align} $$
$$ \begin{align} \widetilde{\phi}(x)&:=\rho_1(\nu(x))\phi(x)+\rho_2(\nu(x))\phi\circ \widetilde{F}^{-1}(x) \\ &=\phi(x)+\rho_2(\nu(x))(\phi\circ\widetilde{F}^{-1}(x)-\phi(x)).\nonumber \end{align} $$
Proposition 2.4. For every fixed
![]() $\chi \in (0,\tfrac 12)$
,
$\chi \in (0,\tfrac 12)$
,
![]() $\sigma \in (0,\tfrac 12(\tfrac 12-\chi ))$
and every
$\sigma \in (0,\tfrac 12(\tfrac 12-\chi ))$
and every
![]() $\eta $
small enough (depending on
$\eta $
small enough (depending on
![]() $\chi $
and
$\chi $
and
![]() $\sigma $
), the function
$\sigma $
), the function
![]() $\widetilde {\phi }$
given by equation (2.14) is well defined on
$\widetilde {\phi }$
given by equation (2.14) is well defined on
![]() $S_{\chi ,\eta }$
and
$S_{\chi ,\eta }$
and
![]() $\widetilde {F}$
-invariant: if
$\widetilde {F}$
-invariant: if
![]() $x, \widetilde {F}(x)\in S_{\chi ,\eta }$
, then
$x, \widetilde {F}(x)\in S_{\chi ,\eta }$
, then
![]() $\widetilde {\phi }(\widetilde {F}(x))=\widetilde {\phi }(x)$
. It is
$\widetilde {\phi }(\widetilde {F}(x))=\widetilde {\phi }(x)$
. It is
![]() $C^{\infty }$
-smooth, and the difference
$C^{\infty }$
-smooth, and the difference
![]() $\widetilde {\phi }(x)-\phi (x)$
is
$\widetilde {\phi }(x)-\phi (x)$
is
![]() $\phi $
-flat on
$\phi $
-flat on
![]() $S_{\chi ,\eta }$
.
$S_{\chi ,\eta }$
.
Proof. Recall that
![]() $\widetilde {F}$
satisfies asymptotic equation (1.13):
$\widetilde {F}$
satisfies asymptotic equation (1.13):
Well-definedness and
![]() $C^{\infty }$
-smoothness of the function
$C^{\infty }$
-smoothness of the function
![]() $\widetilde {\phi }$
on
$\widetilde {\phi }$
on
![]() $S_{\chi ,\eta }$
for small
$S_{\chi ,\eta }$
for small
![]() $\eta $
are obvious. The difference
$\eta $
are obvious. The difference
![]() $\widetilde {\phi }(x)-\phi (x)$
is
$\widetilde {\phi }(x)-\phi (x)$
is
![]() $\phi $
-flat on
$\phi $
-flat on
![]() $S_{\chi ,\eta }$
, by equation (2.14),
$S_{\chi ,\eta }$
, by equation (2.14),
![]() $\phi $
-flatness of the difference
$\phi $
-flatness of the difference
![]() $\phi \circ \widetilde {F}-\phi $
, see equation (1.13), and the fact that the function
$\phi \circ \widetilde {F}-\phi $
, see equation (1.13), and the fact that the function
![]() $\nu (\tau ,\phi )= \tau /\phi $
has partial derivatives of at most polynomial growth in
$\nu (\tau ,\phi )= \tau /\phi $
has partial derivatives of at most polynomial growth in
![]() $\phi $
, as
$\phi $
, as
![]() $(\tau ,\phi )\to 0$
along the sector
$(\tau ,\phi )\to 0$
along the sector
![]() $S_{\chi ,\eta }$
. Let us prove
$S_{\chi ,\eta }$
. Let us prove
![]() $\widetilde {F}$
-invariance of the function
$\widetilde {F}$
-invariance of the function
![]() $\widetilde {\phi }$
for
$\widetilde {\phi }$
for
![]() $\eta $
small enough. For every
$\eta $
small enough. For every
![]() $\delta>0$
and every
$\delta>0$
and every
![]() $\eta>0$
small enough (depending on
$\eta>0$
small enough (depending on
![]() $\delta $
), the inclusion
$\delta $
), the inclusion
![]() $x,\widetilde {F}(x)\in S_{\chi ,\eta }$
implies that
$x,\widetilde {F}(x)\in S_{\chi ,\eta }$
implies that
![]() $x\in \{-\chi \phi <\tau <(\chi +\delta )\phi \}$
, see equation (2.11). Choosing
$x\in \{-\chi \phi <\tau <(\chi +\delta )\phi \}$
, see equation (2.11). Choosing
![]() $\delta <\sigma $
, we get that the latter sector lies in the sector
$\delta <\sigma $
, we get that the latter sector lies in the sector
![]() $\{-\chi \phi <\tau <(\tfrac 12-\sigma )\phi \}$
, since
$\{-\chi \phi <\tau <(\tfrac 12-\sigma )\phi \}$
, since
![]() $\chi +\delta <\chi +\sigma < \tfrac 12-\sigma $
, see equation (2.12). Thus, on the latter sector,
$\chi +\delta <\chi +\sigma < \tfrac 12-\sigma $
, see equation (2.12). Thus, on the latter sector,
![]() $\rho _1\circ \nu \equiv 1$
and
$\rho _1\circ \nu \equiv 1$
and
![]() $\rho _2\circ \nu \equiv 0$
, see equation (2.13). Hence,
$\rho _2\circ \nu \equiv 0$
, see equation (2.13). Hence,
![]() $\widetilde {\phi }(x)=\phi (x)$
, by equation (2.14). Similarly applying the above argument ‘in the inverse time’ yields that the inclusion
$\widetilde {\phi }(x)=\phi (x)$
, by equation (2.14). Similarly applying the above argument ‘in the inverse time’ yields that the inclusion
![]() $x,\widetilde {F}(x)\in S_{\chi ,\eta }$
implies that
$x,\widetilde {F}(x)\in S_{\chi ,\eta }$
implies that
![]() $\widetilde {F}(x)$
lies in the sector
$\widetilde {F}(x)$
lies in the sector
![]() $\{(1-\chi -\delta )\phi <\tau <(1+\chi )\phi \}$
. The latter sector and hence
$\{(1-\chi -\delta )\phi <\tau <(1+\chi )\phi \}$
. The latter sector and hence
![]() $\widetilde {F}(x)$
lie in the sector
$\widetilde {F}(x)$
lie in the sector
![]() $\{(\tfrac 12+\sigma )\phi <\tau <(1+\chi )\phi \}$
, since
$\{(\tfrac 12+\sigma )\phi <\tau <(1+\chi )\phi \}$
, since
Therefore,
![]() $\rho _2\circ \nu (\widetilde {F}(x))=1$
, by equation (2.13), and
$\rho _2\circ \nu (\widetilde {F}(x))=1$
, by equation (2.13), and
![]() $\widetilde {\phi }(\widetilde {F}(x))=\phi \circ \widetilde {F}^{-1}(\widetilde {F}(x))=\phi (x)$
, by equation (2.14). Finally, we get that
$\widetilde {\phi }(\widetilde {F}(x))=\phi \circ \widetilde {F}^{-1}(\widetilde {F}(x))=\phi (x)$
, by equation (2.14). Finally, we get that
![]() $\widetilde {\phi }(x)=\widetilde {\phi }\circ \widetilde {F}(x)$
and hence
$\widetilde {\phi }(x)=\widetilde {\phi }\circ \widetilde {F}(x)$
and hence
![]() $\widetilde {\phi }$
is
$\widetilde {\phi }$
is
![]() $\widetilde {F}$
-invariant. The proposition is proved.
$\widetilde {F}$
-invariant. The proposition is proved.
Proposition 2.4 immediately implies the statement of Proposition 2.3.
2.3 Step 2. Extension by dynamics
Here we show that an
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
![]() $\widetilde {\phi }$
constructed above on a neighborhood of the fundamental domain
$\widetilde {\phi }$
constructed above on a neighborhood of the fundamental domain
![]() $\Delta $
extends along
$\Delta $
extends along
![]() $\widetilde {F}$
-orbits to an
$\widetilde {F}$
-orbits to an
![]() $\widetilde {F}$
-invariant function on a domain W adjacent to
$\widetilde {F}$
-invariant function on a domain W adjacent to
![]() $J=(a,b)\times \{0\}\subset {\mathbb R}^2_{\tau ,\phi }$
. The fact that it is
$J=(a,b)\times \{0\}\subset {\mathbb R}^2_{\tau ,\phi }$
. The fact that it is
![]() $C^\infty $
-smooth on
$C^\infty $
-smooth on
![]() $W\cup J$
and coincides with
$W\cup J$
and coincides with
![]() $\phi $
up to
$\phi $
up to
![]() $\phi $
-flat terms will be proved in the next subsection. It suffices to prove that the function
$\phi $
-flat terms will be proved in the next subsection. It suffices to prove that the function
![]() $\widetilde {\phi }$
extends as above to a rectangle
$\widetilde {\phi }$
extends as above to a rectangle
![]() $(a',b')\times [0,\eta ')$
adjacent to an arbitrary relatively compact subinterval
$(a',b')\times [0,\eta ')$
adjacent to an arbitrary relatively compact subinterval
![]() $J'=(a',b')\times \{0\}\Subset ~J$
. A union of the above rectangles corresponding to an exhaustion of J by a sequence of subintervals
$J'=(a',b')\times \{0\}\Subset ~J$
. A union of the above rectangles corresponding to an exhaustion of J by a sequence of subintervals
![]() $J'$
yields a domain W adjacent to all of J, where the extended function is defined. Therefore, we make the following convention.
$J'$
yields a domain W adjacent to all of J, where the extended function is defined. Therefore, we make the following convention.
Convention 2.5. Everywhere below, we identify the interval
![]() $J=(a,b)\times \{0\}$
with
$J=(a,b)\times \{0\}$
with
![]() $(a,b)$
and sometimes we denote
$(a,b)$
and sometimes we denote
![]() $J=(a,b)\subset {\mathbb R}$
. We consider that J is a finite interval: a, b are finite. We will consider that there exists a
$J=(a,b)\subset {\mathbb R}$
. We consider that J is a finite interval: a, b are finite. We will consider that there exists a
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\widetilde {F}^{\pm 1}$
are diffeomorphisms of the rectangle
$\widetilde {F}^{\pm 1}$
are diffeomorphisms of the rectangle
![]() $J\times [0,\delta )\subset {\mathbb R}^2_{\tau ,\phi }$
onto its images, and the
$J\times [0,\delta )\subset {\mathbb R}^2_{\tau ,\phi }$
onto its images, and the
![]() $\phi $
-flat terms in asymptotic equation (1.13) are uniformly
$\phi $
-flat terms in asymptotic equation (1.13) are uniformly
![]() $\phi $
-flat: the difference
$\phi $
-flat: the difference
![]() $\widetilde {F}(\tau ,\phi )-(\tau +\phi ,\phi )$
converges to zero uniformly in
$\widetilde {F}(\tau ,\phi )-(\tau +\phi ,\phi )$
converges to zero uniformly in
![]() $\tau \in J$
, and every partial derivative (of any order) also converges to zero uniformly, as
$\tau \in J$
, and every partial derivative (of any order) also converges to zero uniformly, as
![]() $\phi \to 0$
. A priori,
$\phi \to 0$
. A priori,
![]() $\phi $
-flatness of a
$\phi $
-flatness of a
![]() $C^\infty $
-smooth function on
$C^\infty $
-smooth function on
![]() $J\times [0,\delta )$
, which means triviality of all its jets at all points in
$J\times [0,\delta )$
, which means triviality of all its jets at all points in
![]() $J\times \{0\}$
, is weaker than its uniform
$J\times \{0\}$
, is weaker than its uniform
![]() $\phi $
-flatness. However, it implies uniform
$\phi $
-flatness. However, it implies uniform
![]() $\phi $
-flatness on compact subsegments in J, see Definition 1.28. Hence, one can achieve uniform flatness replacing J by its relatively compact subinterval. Under this assumption, the above difference and its differential are both uniformly
$\phi $
-flatness on compact subsegments in J, see Definition 1.28. Hence, one can achieve uniform flatness replacing J by its relatively compact subinterval. Under this assumption, the above difference and its differential are both uniformly
![]() $o(\phi ^m)$
in
$o(\phi ^m)$
in
![]() $\tau \in J$
for each individual
$\tau \in J$
for each individual
![]() $m\in {\mathbb N}$
.
$m\in {\mathbb N}$
.
The next proposition describes asymptotics of two-sided
![]() $\widetilde {F}$
-orbits.
$\widetilde {F}$
-orbits.
Proposition 2.6. For every
![]() $\eta $
small enough and
$\eta $
small enough and
![]() $x:=(\tau _0,\phi _0)\in J\times [0,\eta )$
:
$x:=(\tau _0,\phi _0)\in J\times [0,\eta )$
:
-
(a) the iterates
 $\widetilde {F}^j(x)=(\tau _j,\phi _j)$
are well defined for all
$\widetilde {F}^j(x)=(\tau _j,\phi _j)$
are well defined for all
 $j\geq 0$
,
$j\geq 0$
,
 $j\leq N_+$
, where
$j\leq N_+$
, where
 ${N_+=N_+(x)}$
is the maximal number j for which
${N_+=N_+(x)}$
is the maximal number j for which
 $\tau _j< b$
;
$\tau _j< b$
; -
(b) the inverse iterates
 $\widetilde {F}^{-j}(x)=(\tau _{-j},\phi _{-j})$
are well defined for all
$\widetilde {F}^{-j}(x)=(\tau _{-j},\phi _{-j})$
are well defined for all
 $j\leq N_{-}$
, where
$j\leq N_{-}$
, where
 $N_-=N_-(x)$
is the maximal number j for which
$N_-=N_-(x)$
is the maximal number j for which
 $\tau _{-j}> a$
;
$\tau _{-j}> a$
; -
(c)
 $\phi _j=\phi _0(1+o(1))$
uniformly in
$\phi _j=\phi _0(1+o(1))$
uniformly in
 $\tau _0$
and
$\tau _0$
and
 $j\in [-N_-,N_+]$
, as
$j\in [-N_-,N_+]$
, as
 $\phi _0\to 0$
;
$\phi _0\to 0$
; -
(d) the points
 $\tau _j$
form an asymptotic arithmetic progression:
$\tau _j$
form an asymptotic arithmetic progression:
 $\tau _{j+1}-\tau _j= \phi _0(1+o(1))$
uniformly in
$\tau _{j+1}-\tau _j= \phi _0(1+o(1))$
uniformly in
 $\tau _0\in J$
and in
$\tau _0\in J$
and in
 $j\in [-N_-,N_+-1]$
, as
$j\in [-N_-,N_+-1]$
, as
 $\phi _0\to 0$
.
$\phi _0\to 0$
.
Proof. Consider two lines and segments through x:
Claim 2. For every
![]() $x=(\tau _0,\phi _0)\in J\times [0,2\eta )$
with
$x=(\tau _0,\phi _0)\in J\times [0,2\eta )$
with
![]() $\phi _0$
small enough:
$\phi _0$
small enough:
-
(e) the image
 $\widetilde {F}({\unicode{x3bb} } _{\pm })$
is disjoint from
$\widetilde {F}({\unicode{x3bb} } _{\pm })$
is disjoint from
 ${\unicode{x3bb} } _{\pm }$
and lies on its right;
${\unicode{x3bb} } _{\pm }$
and lies on its right; -
(f) the image
 $\widetilde {F}^{-1}({\unicode{x3bb} } _{\pm })$
is disjoint from
$\widetilde {F}^{-1}({\unicode{x3bb} } _{\pm })$
is disjoint from
 ${\unicode{x3bb} } _{\pm }$
and lies on its left;
${\unicode{x3bb} } _{\pm }$
and lies on its left; -
(g) the right sector
 $S_{+}(x)$
bounded by the right subintervals in
$S_{+}(x)$
bounded by the right subintervals in
 ${\unicode{x3bb} } _{\pm }$
with vertex x is
${\unicode{x3bb} } _{\pm }$
with vertex x is
 $\widetilde {F}$
-invariant;
$\widetilde {F}$
-invariant; -
(h) the left sector
 $S_{-}(x)$
bounded by the left subintervals in
$S_{-}(x)$
bounded by the left subintervals in
 ${\unicode{x3bb} } _{\pm }$
with vertex x is
${\unicode{x3bb} } _{\pm }$
with vertex x is
 $\widetilde {F}^{-1}$
-invariant.
$\widetilde {F}^{-1}$
-invariant.
Proof. If
![]() $\eta $
is small enough, then
$\eta $
is small enough, then
![]() $\widetilde {F}^{\pm 1}$
are well defined on
$\widetilde {F}^{\pm 1}$
are well defined on
![]() $J\times [0,3\eta )$
. If
$J\times [0,3\eta )$
. If
![]() $\phi _0$
is small enough, then each
$\phi _0$
is small enough, then each
![]() ${\unicode{x3bb} } _{\pm }$
is projected to all of J, and the
${\unicode{x3bb} } _{\pm }$
is projected to all of J, and the
![]() $\phi $
-coordinates of all its points are uniformly asymptotically equivalent to
$\phi $
-coordinates of all its points are uniformly asymptotically equivalent to
![]() $\phi _0$
, that is, their ratio with
$\phi _0$
, that is, their ratio with
![]() $\phi _0$
tends uniformly to 1 (finiteness of J). The map
$\phi _0$
tends uniformly to 1 (finiteness of J). The map
![]() $\widetilde {F}$
moves a point
$\widetilde {F}$
moves a point
![]() $z=(\tau ,\phi )\in {\unicode{x3bb} }_{\pm }$
to
$z=(\tau ,\phi )\in {\unicode{x3bb} }_{\pm }$
to
![]() $y:=(\tau +\phi ,\phi )$
up to a
$y:=(\tau +\phi ,\phi )$
up to a
![]() $\phi $
-flat term, which is
$\phi $
-flat term, which is
![]() $o(\phi _0^m)$
for every
$o(\phi _0^m)$
for every
![]() $m\in {\mathbb N}$
. However, the distance of the latter point y to the line
$m\in {\mathbb N}$
. However, the distance of the latter point y to the line
![]() $L_{\pm }$
is equal to
$L_{\pm }$
is equal to
![]() $\phi \simeq \phi _0$
times the
$\phi \simeq \phi _0$
times the
![]() $\lvert \sin \rvert $
of the azimuth of the line
$\lvert \sin \rvert $
of the azimuth of the line
![]() $L_{\pm }$
. The latter
$L_{\pm }$
. The latter
![]() $\lvert \sin \rvert $
is asymptotic to
$\lvert \sin \rvert $
is asymptotic to
![]() $\phi _0^{4}$
, and hence, is greater than
$\phi _0^{4}$
, and hence, is greater than
![]() $\tfrac 12\phi _0^{4}$
, whenever
$\tfrac 12\phi _0^{4}$
, whenever
![]() $\phi _0<1$
is small enough. Thus,
$\phi _0<1$
is small enough. Thus,
![]() ${\operatorname {dist}}(y,L_{\pm })\geq \tfrac 13\phi _0^5$
. Therefore, adding a term
${\operatorname {dist}}(y,L_{\pm })\geq \tfrac 13\phi _0^5$
. Therefore, adding a term
![]() $o(\phi _0^m)$
,
$o(\phi _0^m)$
,
![]() $m\geq 5$
, to y will not allow to cross
$m\geq 5$
, to y will not allow to cross
![]() $L_{\pm }$
, and we will get a point lying on the same, right side from the line
$L_{\pm }$
, and we will get a point lying on the same, right side from the line
![]() $L_{\pm }$
, as y. The cases of lines
$L_{\pm }$
, as y. The cases of lines
![]() $L_{\mp }$
and inverse iterates are treated analogously. Statements (e) and (f) are proved. They immediately imply statements (g) and (h).
$L_{\mp }$
and inverse iterates are treated analogously. Statements (e) and (f) are proved. They immediately imply statements (g) and (h).
Let
![]() $\eta \in (0,\tfrac 18)$
be small enough so that
$\eta \in (0,\tfrac 18)$
be small enough so that
![]() $\widetilde {F}$
is defined on the rectangle
$\widetilde {F}$
is defined on the rectangle
![]() $\Pi :=J\times [0,3\eta )$
and for every
$\Pi :=J\times [0,3\eta )$
and for every
![]() $x\in \Pi $
with
$x\in \Pi $
with
![]() $\phi _0=\phi (x)\in [0,2\eta ]$
, the sector
$\phi _0=\phi (x)\in [0,2\eta ]$
, the sector
![]() $S_{+}(x)$
contains the points
$S_{+}(x)$
contains the points
![]() ${x_j=\widetilde {F}^j(x)}$
until they go out of
${x_j=\widetilde {F}^j(x)}$
until they go out of
![]() $\Pi $
(Claim 2(g)). The intersection
$\Pi $
(Claim 2(g)). The intersection
![]() $S_{+}(x)\cap \partial \Pi $
is contained in the right lateral side
$S_{+}(x)\cap \partial \Pi $
is contained in the right lateral side
![]() $\{ b\}\times [0,3\eta )$
. Therefore, the first j for which
$\{ b\}\times [0,3\eta )$
. Therefore, the first j for which
![]() $x_j$
goes out of
$x_j$
goes out of
![]() $\Pi $
is the one for which
$\Pi $
is the one for which
![]() $\tau (x_j)\geq b$
. This proves statement (a) of Proposition 2.6. The proof of statement (b) is analogous. For every
$\tau (x_j)\geq b$
. This proves statement (a) of Proposition 2.6. The proof of statement (b) is analogous. For every
![]() $x\in \Pi $
with
$x\in \Pi $
with
![]() $\phi _0=\phi (x)$
small enough, the above inclusion
$\phi _0=\phi (x)$
small enough, the above inclusion
![]() ${x_j\in S_{+}(x)}$
holds for
${x_j\in S_{+}(x)}$
holds for
![]() $j=1,\ldots ,N_+$
. It implies statement (c) for the above j, by the definition of the sector
$j=1,\ldots ,N_+$
. It implies statement (c) for the above j, by the definition of the sector
![]() $S_{+}$
. The proof of statement (c) for
$S_{+}$
. The proof of statement (c) for
![]() $j=-N_-,\ldots ,-1$
is analogous. Statement (d) follows from statement (c), since
$j=-N_-,\ldots ,-1$
is analogous. Statement (d) follows from statement (c), since
![]() $\tau \circ \widetilde {F}(x)-\tau (x)=\phi (x)+{\operatorname {flat}}(\phi (x))$
, see equation (1.13). Proposition 2.6 is proved.
$\tau \circ \widetilde {F}(x)-\tau (x)=\phi (x)+{\operatorname {flat}}(\phi (x))$
, see equation (1.13). Proposition 2.6 is proved.
Corollary 2.7.
-
(1) For every
 $\eta>0$
small enough, each point
$\eta>0$
small enough, each point
 $x=(\tau _0,\phi _0)\in J\times [0, (2\eta)/3)$
has two-sided orbit lying in
$x=(\tau _0,\phi _0)\in J\times [0, (2\eta)/3)$
has two-sided orbit lying in
 $J\times [0,\eta )$
and consisting of points
$J\times [0,\eta )$
and consisting of points
 $x_j$
,
$x_j$
,
 $j\in [-N_-(x),N_+(x)]$
, with
$j\in [-N_-(x),N_+(x)]$
, with
 $\phi _j\simeq \phi _0$
, as
$\phi _j\simeq \phi _0$
, as
 $\phi _0\to 0$
; the latter asymptotics is uniform in the above j and in
$\phi _0\to 0$
; the latter asymptotics is uniform in the above j and in
 $\tau _0\in J$
.
$\tau _0\in J$
. -
(2) Let
 $\Delta $
denote the fundamental domain (curvilinear triangle) for the map
$\Delta $
denote the fundamental domain (curvilinear triangle) for the map
 $\widetilde {F}$
from Proposition 2.2(iii). Let
$\widetilde {F}$
from Proposition 2.2(iii). Let
 $\widehat \Delta $
denote the complement of the closure
$\widehat \Delta $
denote the complement of the closure
 $\overline \Delta $
to the union of its vertex
$\overline \Delta $
to the union of its vertex
 $(0,0)$
and the opposite side. If
$(0,0)$
and the opposite side. If
 $\eta>0$
is small enough, then the domain W saturated by the above two-sided orbits of points in
$\eta>0$
is small enough, then the domain W saturated by the above two-sided orbits of points in
 $\widehat \Delta $
lies in
$\widehat \Delta $
lies in
 $J\times [0, (2\eta)/3)$
and contains the strip
$J\times [0, (2\eta)/3)$
and contains the strip
 $J\times (0, \eta /4)$
.
$J\times (0, \eta /4)$
. -
(3) The orbit of each point in W contains either a unique point lying in the fundamental domain
 $\Delta $
, or two subsequent points lying in its lateral boundary curves (glued by
$\Delta $
, or two subsequent points lying in its lateral boundary curves (glued by
 $\widetilde {F}$
).
$\widetilde {F}$
). -
(4) Each
 $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
 $\widetilde {\phi }$
on
$\widetilde {\phi }$
on
 $\widehat \Delta $
extends to a unique
$\widehat \Delta $
extends to a unique
 $\widetilde {F}$
-invariant function on W as a function constant along the latter orbits.
$\widetilde {F}$
-invariant function on W as a function constant along the latter orbits.
The corollary follows immediately from Proposition 2.6. Step 2 is done.
2.4 Step 3. Regularity and flatness. End of proof of Theorem 1.30(1)
Here we will prove the following lemma, which will imply statement (1) of Theorem 1.30.
Lemma 2.8. Let in Corollary 2.7 the function
![]() $\widetilde {\phi }$
on
$\widetilde {\phi }$
on
![]() $\widehat \Delta $
be the restriction to
$\widehat \Delta $
be the restriction to
![]() $\widehat \Delta $
of a
$\widehat \Delta $
of a
![]() $C^{\infty }$
-smooth
$C^{\infty }$
-smooth
![]() $\widetilde {F}$
-invariant function defined on a neighborhood of
$\widetilde {F}$
-invariant function defined on a neighborhood of
![]() $\widehat \Delta $
. Let the function
$\widehat \Delta $
. Let the function
![]() $\widetilde {\phi }(\tau ,\phi )-\phi $
be flat on
$\widetilde {\phi }(\tau ,\phi )-\phi $
be flat on
![]() $\widehat \Delta $
: it tends to zero with all its partial derivatives, as
$\widehat \Delta $
: it tends to zero with all its partial derivatives, as
![]() $(\tau ,\phi )\in \widehat \Delta $
tends to zero. Consider its
$(\tau ,\phi )\in \widehat \Delta $
tends to zero. Consider its
![]() $\widetilde {F}$
-invariant extension to the above domain W from Corollary 2.7(4), and let us denote the extended function by the same symbol
$\widetilde {F}$
-invariant extension to the above domain W from Corollary 2.7(4), and let us denote the extended function by the same symbol
![]() $\widetilde {\phi }$
. The difference
$\widetilde {\phi }$
. The difference
![]() $\widetilde {\phi }(\tau ,\phi )-\phi $
is
$\widetilde {\phi }(\tau ,\phi )-\phi $
is
![]() $C^{\infty }$
-smooth on
$C^{\infty }$
-smooth on
![]() $W\cup J$
, and it is uniformly
$W\cup J$
, and it is uniformly
![]() $\phi $
-flat (see Convention 2.5).
$\phi $
-flat (see Convention 2.5).
Proof. For every point
![]() $x=(\tau ,\phi )\in W$
, there exists an
$x=(\tau ,\phi )\in W$
, there exists an
![]() $N=N(x)\in {\mathbb Z}$
such that
$N=N(x)\in {\mathbb Z}$
such that
![]() ${\widetilde {F}^N(x)\in \widehat \Delta }$
. The latter image
${\widetilde {F}^N(x)\in \widehat \Delta }$
. The latter image
![]() $\widetilde {F}^N(x)$
lies in the definition domain of the initial function
$\widetilde {F}^N(x)$
lies in the definition domain of the initial function
![]() $\widetilde {\phi }$
(which is defined on a neighborhood of
$\widetilde {\phi }$
(which is defined on a neighborhood of
![]() $\widehat \Delta $
), and
$\widehat \Delta $
), and
![]() $\widetilde {\phi }(x)=\widetilde {\phi }_N(x):=\widetilde {\phi }(\widetilde {F}^N(x))$
, by definition. This immediately implies
$\widetilde {\phi }(x)=\widetilde {\phi }_N(x):=\widetilde {\phi }(\widetilde {F}^N(x))$
, by definition. This immediately implies
![]() $C^{\infty }$
-smoothness of the extended function
$C^{\infty }$
-smoothness of the extended function
![]() $\widetilde {\phi }$
on W. Let us prove its
$\widetilde {\phi }$
on W. Let us prove its
![]() $\phi $
-flatness. This will automatically imply
$\phi $
-flatness. This will automatically imply
![]() $C^{\infty }$
-smoothness at points of the boundary interval J. To do this, we use the asymptotics
$C^{\infty }$
-smoothness at points of the boundary interval J. To do this, we use the asymptotics
 $$ \begin{align} d\widetilde{F}(\tau,\phi)&=A+{\operatorname{flat}}(\phi),\quad \ A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1 \end{matrix}\bigg); \end{align} $$
$$ \begin{align} d\widetilde{F}(\tau,\phi)&=A+{\operatorname{flat}}(\phi),\quad \ A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1 \end{matrix}\bigg); \end{align} $$
 $$ \begin{align} \!\!N(x) =N(\tau,\phi)=O\bigg(\frac1\phi\bigg).\qquad \end{align} $$
$$ \begin{align} \!\!N(x) =N(\tau,\phi)=O\bigg(\frac1\phi\bigg).\qquad \end{align} $$
Here the flat term in equation (2.15) is uniformly flat, see Convention 2.5. Equation (2.15) follows from equation (1.13). Equation (2.16) holds, since
![]() $N\leq N_++N_-=O(1/\phi )$
, which follows from Proposition 2.6(d).
$N\leq N_++N_-=O(1/\phi )$
, which follows from Proposition 2.6(d).
We study the derivatives of the functions
![]() $\widetilde {\phi }_N-\phi $
,
$\widetilde {\phi }_N-\phi $
,
![]() $N=N(x)$
, at the point
$N=N(x)$
, at the point
![]() $x=(\tau ,\phi )$
, as functions in x with fixed N chosen as above for this concrete x. To prove uniform flatness, we have to show that all its partial derivatives tend to zero uniformly in
$x=(\tau ,\phi )$
, as functions in x with fixed N chosen as above for this concrete x. To prove uniform flatness, we have to show that all its partial derivatives tend to zero uniformly in
![]() $\tau \in J$
, as
$\tau \in J$
, as
![]() $\phi \to 0$
. We prove this statement for the first derivatives (Step 1) and then for the higher derivatives (Step 2).
$\phi \to 0$
. We prove this statement for the first derivatives (Step 1) and then for the higher derivatives (Step 2).
Without loss of generality, everywhere below, we consider that
![]() $N\geq 1$
, that is, x lies on the left from the sector
$N\geq 1$
, that is, x lies on the left from the sector
![]() $\Delta $
: for negative N, the proof is analogous.
$\Delta $
: for negative N, the proof is analogous.
Step 1. The first derivatives. The initial function
![]() $\widetilde {\phi }$
defined on a neighborhood of the set
$\widetilde {\phi }$
defined on a neighborhood of the set
![]() $\widehat \Delta $
is already known to be
$\widehat \Delta $
is already known to be
![]() $\phi $
-flat on
$\phi $
-flat on
![]() $\widehat \Delta $
. The differential of the composition
$\widehat \Delta $
. The differential of the composition
![]() $\widetilde {\phi }_N=\widetilde {\phi }\circ \widetilde {F}^N$
at the point x,
$\widetilde {\phi }_N=\widetilde {\phi }\circ \widetilde {F}^N$
at the point x,
![]() $N=N(x)$
, is equal to
$N=N(x)$
, is equal to
Proposition 2.9. For every sequence of points
![]() $x(k)=(\tau _{0k},\phi _{0k})\in W$
with
$x(k)=(\tau _{0k},\phi _{0k})\in W$
with
![]() $\phi _{0k}\to 0$
, as
$\phi _{0k}\to 0$
, as
![]() $k\to \infty $
, and numbers
$k\to \infty $
, and numbers
![]() $N_k=N(x(k))\in {\mathbb N}$
with
$N_k=N(x(k))\in {\mathbb N}$
with
![]() $\widetilde {F}^{N_k}(x(k))\in \widehat \Delta $
, the difference
$\widetilde {F}^{N_k}(x(k))\in \widehat \Delta $
, the difference
![]() $d(\widetilde {\phi }\circ \widetilde {F}^{N_k})(x(k))-d\phi $
tends to zero, as
$d(\widetilde {\phi }\circ \widetilde {F}^{N_k})(x(k))-d\phi $
tends to zero, as
![]() $k\to \infty $
.
$k\to \infty $
.
Proposition 2.9 implies uniform convergence to zero of the first derivatives.
In its proof (given below), we use the following asymptotics of differential
![]() $d\widetilde {F}(\widetilde {F}^j(x))$
and technical proposition on matrix products. We denote
$d\widetilde {F}(\widetilde {F}^j(x))$
and technical proposition on matrix products. We denote
Proposition 2.10. Let
![]() $x\kern1.4pt{=}\kern1.4pt(\tau _0,\phi _0)\kern1.4pt{\in}\kern1.4pt J\kern1.4pt{\times}\kern1.4pt (0, \eta /4)$
,
$x\kern1.4pt{=}\kern1.4pt(\tau _0,\phi _0)\kern1.4pt{\in}\kern1.4pt J\kern1.4pt{\times}\kern1.4pt (0, \eta /4)$
,
![]() $x_j\kern1.4pt{=}\kern1.4pt(\tau _j,\phi _j)\kern1.4pt{:=}\kern1.4pt \widetilde {F}^j(x)$
,
$x_j\kern1.4pt{=}\kern1.4pt(\tau _j,\phi _j)\kern1.4pt{:=}\kern1.4pt \widetilde {F}^j(x)$
,
![]() $j\kern1.4pt{=}\kern1.4pt 0,\ldots , N(x)$
. For every
$j\kern1.4pt{=}\kern1.4pt 0,\ldots , N(x)$
. For every
![]() $m\in {\mathbb N}$
, one has
$m\in {\mathbb N}$
, one has
 $$ \begin{align} M(\tau_j,\phi_j)=A+o(\phi_0^m),\quad \text{as } \phi_0\to0; \quad A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\bigg), \end{align} $$
$$ \begin{align} M(\tau_j,\phi_j)=A+o(\phi_0^m),\quad \text{as } \phi_0\to0; \quad A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1\end{matrix}\bigg), \end{align} $$
uniformly in
![]() $j=1,\ldots ,N(x)$
and in
$j=1,\ldots ,N(x)$
and in
![]() $\tau _0\in J$
for each individual m.
$\tau _0\in J$
for each individual m.
Proposition 2.11. Consider arbitrary sequences of numbers
![]() $\phi _{0k}>0$
,
$\phi _{0k}>0$
,
![]() $N_k\in {\mathbb N}$
,
$N_k\in {\mathbb N}$
,
![]() $\phi _{0k}\to 0$
,
$\phi _{0k}\to 0$
,
![]() $N_k=O(1/{\phi _{0k}})$
, as
$N_k=O(1/{\phi _{0k}})$
, as
![]() $k\to \infty $
, and matrix collections
$k\to \infty $
, and matrix collections
 $$ \begin{align} M_{j;k}=A+o(\phi_{0k}^m) \quad \text{for every } m\in{\mathbb N};\quad A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1 \end{matrix}\bigg). \end{align} $$
$$ \begin{align} M_{j;k}=A+o(\phi_{0k}^m) \quad \text{for every } m\in{\mathbb N};\quad A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1 \end{matrix}\bigg). \end{align} $$
Here the latter asymptotics is uniform in
![]() $j=1,\ldots ,N_k$
for each individual m, as
$j=1,\ldots ,N_k$
for each individual m, as
![]() $k\to \infty $
. Then the products of the matrices
$k\to \infty $
. Then the products of the matrices
![]() $M_{j;k}$
have the asymptotics
$M_{j;k}$
have the asymptotics
 $$ \begin{align} \widehat M_k:=M_{N_k;k}\cdots M_{1;k} =\bigg(\begin{matrix} 1 & N_k\\ 0 & 1\end{matrix}\bigg) + o(\phi_{0k}^m)\quad \text{for every} \ m\in{\mathbb N}. \end{align} $$
$$ \begin{align} \widehat M_k:=M_{N_k;k}\cdots M_{1;k} =\bigg(\begin{matrix} 1 & N_k\\ 0 & 1\end{matrix}\bigg) + o(\phi_{0k}^m)\quad \text{for every} \ m\in{\mathbb N}. \end{align} $$
Proof. Conjugation by the diagonal matrix
![]() $H_k:={\operatorname {diag}} (1,\phi _{0k}^{-1})$
transforms the matrices
$H_k:={\operatorname {diag}} (1,\phi _{0k}^{-1})$
transforms the matrices
![]() $M_{j;k}$
and their product respectively to the following matrices:
$M_{j;k}$
and their product respectively to the following matrices:
 $$ \begin{align*} \widetilde{M}_{j;k}=B_k+o(\phi_{0k}^m),\quad B_k=\bigg(\begin{matrix} 1 & \phi_{0k}\\ 0 & 1 \end{matrix}\bigg);\quad \widetilde{M}_k:=\widetilde{M}_{N_k;k}\cdots \widetilde{M}_{1;k}. \end{align*} $$
$$ \begin{align*} \widetilde{M}_{j;k}=B_k+o(\phi_{0k}^m),\quad B_k=\bigg(\begin{matrix} 1 & \phi_{0k}\\ 0 & 1 \end{matrix}\bigg);\quad \widetilde{M}_k:=\widetilde{M}_{N_k;k}\cdots \widetilde{M}_{1;k}. \end{align*} $$
Claim 3. One has
 $$ \begin{align}\widetilde{M}_k=B_k^{N_k}+o(\phi_{0k}^m)=\bigg(\begin{matrix} 1 & N_k\phi_{0k}\\ 0 & 1 \end{matrix}\bigg)+o(\phi_{0k}^m).\end{align} $$
$$ \begin{align}\widetilde{M}_k=B_k^{N_k}+o(\phi_{0k}^m)=\bigg(\begin{matrix} 1 & N_k\phi_{0k}\\ 0 & 1 \end{matrix}\bigg)+o(\phi_{0k}^m).\end{align} $$
Proof. Without loss of generality, we can and will consider that
![]() $N_k\phi _{0k}\to C\in {\mathbb R}_{\geq 0}$
, passing to a subsequence, since
$N_k\phi _{0k}\to C\in {\mathbb R}_{\geq 0}$
, passing to a subsequence, since
![]() $N_k=O(1/{\phi _{0k}})$
, by assumption. Let
$N_k=O(1/{\phi _{0k}})$
, by assumption. Let
![]() ${\mathcal {UT}}\subset {\operatorname {GL}} _2({\mathbb R})$
denote the one-parametric subgroup of unipotent upper triangular matrices. Consider the tangent vector
${\mathcal {UT}}\subset {\operatorname {GL}} _2({\mathbb R})$
denote the one-parametric subgroup of unipotent upper triangular matrices. Consider the tangent vector
 $$ \begin{align*}V=\bigg(\begin{matrix} 0 & 1\\ 0 & 0\end{matrix}\bigg)\in T_1{\mathcal{UT}}\subset T_1{\operatorname{GL}} _2({\mathbb R}). \end{align*} $$
$$ \begin{align*}V=\bigg(\begin{matrix} 0 & 1\\ 0 & 0\end{matrix}\bigg)\in T_1{\mathcal{UT}}\subset T_1{\operatorname{GL}} _2({\mathbb R}). \end{align*} $$
Let us extend it to a left-invariant vector field on
![]() ${\operatorname {GL}} _2({\mathbb R})$
, which is tangent to the
${\operatorname {GL}} _2({\mathbb R})$
, which is tangent to the
![]() ${\mathcal {UT}}$
-orbits under right multiplication action. Take a small transverse section
${\mathcal {UT}}$
-orbits under right multiplication action. Take a small transverse section
![]() $S\subset {\operatorname {GL}} _2({\mathbb R})$
passing through the identity and consider the subset
$S\subset {\operatorname {GL}} _2({\mathbb R})$
passing through the identity and consider the subset
![]() $\mathcal W\subset {\operatorname {GL}} _2({\mathbb R})$
foliated by arcs of phase curves of the field V starting in S and parameterized by time segment
$\mathcal W\subset {\operatorname {GL}} _2({\mathbb R})$
foliated by arcs of phase curves of the field V starting in S and parameterized by time segment
![]() $[0,2C+1]$
. The subset
$[0,2C+1]$
. The subset
![]() $\mathcal W$
is a bordered domain (flowbox) diffeomorphic to the product
$\mathcal W$
is a bordered domain (flowbox) diffeomorphic to the product
![]() $S\times [0,2C+1]$
via the diffeomorphism sending a point
$S\times [0,2C+1]$
via the diffeomorphism sending a point
![]() $y\in \mathcal W$
to the pair
$y\in \mathcal W$
to the pair
![]() $(s(y),t(y))$
such that the orbit issued from the point
$(s(y),t(y))$
such that the orbit issued from the point
![]() $s(y)\in S$
arrives to y in time
$s(y)\in S$
arrives to y in time
![]() $t(y)$
. Fix an arbitrary
$t(y)$
. Fix an arbitrary
![]() $m\geq 3$
. In the new chart
$m\geq 3$
. In the new chart
![]() $(s,t)$
, the multiplication by a matrix
$(s,t)$
, the multiplication by a matrix
![]() $\widetilde {M}_{j;k}=B_k+o(\phi _{0k}^m)$
from the right moves a point
$\widetilde {M}_{j;k}=B_k+o(\phi _{0k}^m)$
from the right moves a point
![]() $(s,t)$
to the point
$(s,t)$
to the point
![]() $(s,t+\phi _{0k})$
up to a small correction of order
$(s,t+\phi _{0k})$
up to a small correction of order
![]() $o(\phi _{0k}^m)$
. Therefore, the multiplication by
$o(\phi _{0k}^m)$
. Therefore, the multiplication by
![]() $N_k\simeq ({C+o(1)})/{\phi _{0k}}$
similar matrices
$N_k\simeq ({C+o(1)})/{\phi _{0k}}$
similar matrices
![]() $\widetilde {M}_{j;k}$
with the
$\widetilde {M}_{j;k}$
with the
![]() $o(\phi _{0k}^m)$
in their asymptotics being uniform in j moves a point
$o(\phi _{0k}^m)$
in their asymptotics being uniform in j moves a point
![]() $(s,t)$
to a point
$(s,t)$
to a point
![]() $(s,t+N_k\phi _{0k})$
up to a correction of order
$(s,t+N_k\phi _{0k})$
up to a correction of order
![]() $N_ko(\phi _{0k}^m)=o(\phi _{0k}^{m-1})$
. This implies equation (2.21) with m replaced by
$N_ko(\phi _{0k}^m)=o(\phi _{0k}^{m-1})$
. This implies equation (2.21) with m replaced by
![]() $m-1$
. Taking into account that m can be chosen arbitrary, this proves equation (2.21).
$m-1$
. Taking into account that m can be chosen arbitrary, this proves equation (2.21).
Conjugating equation (2.21) by the matrix
![]() $H^{-1}_k$
and taking into account that
$H^{-1}_k$
and taking into account that
![]() $m\in {\mathbb N}$
is arbitrary yields equation (2.20) and proves Proposition 2.11.
$m\in {\mathbb N}$
is arbitrary yields equation (2.20) and proves Proposition 2.11.
Proof of Proposition 2.9
For
![]() $z\in \widehat \Delta $
, set
$z\in \widehat \Delta $
, set
 $$ \begin{align*} St(z):=\bigg(\frac{\partial\widetilde{\phi}}{\partial\tau},\frac{\partial\widetilde{\phi}}{\partial\phi}\bigg)(z). \end{align*} $$
$$ \begin{align*} St(z):=\bigg(\frac{\partial\widetilde{\phi}}{\partial\tau},\frac{\partial\widetilde{\phi}}{\partial\phi}\bigg)(z). \end{align*} $$
The string of the first partial derivatives of the function
![]() $\widetilde {\phi }_N=\widetilde {\phi }\circ \widetilde {F}^N(x)$
,
$\widetilde {\phi }_N=\widetilde {\phi }\circ \widetilde {F}^N(x)$
,
![]() $N=N(x)$
, is equal to the product
$N=N(x)$
, is equal to the product
by
![]() $\phi $
-flatness of the initial function
$\phi $
-flatness of the initial function
![]() $\widetilde {\phi }$
on
$\widetilde {\phi }$
on
![]() $\widehat \Delta $
and by the uniform asymptotics
$\widehat \Delta $
and by the uniform asymptotics
![]() $\phi _j=\phi _0(1+o(1))$
,
$\phi _j=\phi _0(1+o(1))$
,
![]() $j=1,\ldots ,N$
(Proposition 2.6(c)).
$j=1,\ldots ,N$
(Proposition 2.6(c)).
Take arbitrary sequence of points
![]() $x(k):=(\tau _{0k},\phi _{0k})$
,
$x(k):=(\tau _{0k},\phi _{0k})$
,
![]() $\tau _{0k}\in J$
,
$\tau _{0k}\in J$
,
![]() $\phi _{0k}\to 0$
, as
$\phi _{0k}\to 0$
, as
![]() $k\to \infty $
. Set
$k\to \infty $
. Set
The sequence of collections of Jacobian matrices
![]() $M_{j+1;k}:=M(\tau _{jk},\phi _{jk})$
,
$M_{j+1;k}:=M(\tau _{jk},\phi _{jk})$
,
![]() $j=0,\ldots , N_k-1$
, satisfy the conditions of Proposition 2.11, by equations (2.16) and (2.18). Therefore, their product
$j=0,\ldots , N_k-1$
, satisfy the conditions of Proposition 2.11, by equations (2.16) and (2.18). Therefore, their product
![]() $\widehat M_k$
, which is the Jacobian matrix of the differential
$\widehat M_k$
, which is the Jacobian matrix of the differential
![]() $d\widetilde {F}^{N_k}(x(k))$
, has asymptotics in equation (2.20):
$d\widetilde {F}^{N_k}(x(k))$
, has asymptotics in equation (2.20):
 $$ \begin{align}\widehat M_k:= \text{ the Jacobian matrix of } d\widetilde{F}^{N_k}(x(k)) = \bigg(\begin{matrix} 1 & N_k\\ 0 & 1\end{matrix}\bigg) + o(\phi_{0k}^m). \end{align} $$
$$ \begin{align}\widehat M_k:= \text{ the Jacobian matrix of } d\widetilde{F}^{N_k}(x(k)) = \bigg(\begin{matrix} 1 & N_k\\ 0 & 1\end{matrix}\bigg) + o(\phi_{0k}^m). \end{align} $$
Thus, the matrix-string of the differential
![]() $d\widetilde {\phi }_{N_k}(\tau _{0k},\phi _{0k})$
is the product
$d\widetilde {\phi }_{N_k}(\tau _{0k},\phi _{0k})$
is the product
 $$ \begin{align*} St(\tau_{N_k},\phi_{N_k})\widehat M_k = ((0,1) + o(\phi_{0k}^m)) \bigg(\begin{matrix} 1 & N_k\\ 0 & 1 \end{matrix}\bigg) + o(\phi_{0k}^m) = (0,1) + o(\phi_{0k}^{m-1}), \end{align*} $$
$$ \begin{align*} St(\tau_{N_k},\phi_{N_k})\widehat M_k = ((0,1) + o(\phi_{0k}^m)) \bigg(\begin{matrix} 1 & N_k\\ 0 & 1 \end{matrix}\bigg) + o(\phi_{0k}^m) = (0,1) + o(\phi_{0k}^{m-1}), \end{align*} $$
since
![]() $N_k=O(1/{\phi _{0k}})$
, see equation (2.16). For
$N_k=O(1/{\phi _{0k}})$
, see equation (2.16). For
![]() $m=2$
, we get that the differential
$m=2$
, we get that the differential
![]() $d(\widetilde {\phi }_{N_k}(\tau ,\phi )-\phi )$
taken at the point
$d(\widetilde {\phi }_{N_k}(\tau ,\phi )-\phi )$
taken at the point
![]() $x(k)$
tends to zero, as
$x(k)$
tends to zero, as
![]() $k\to \infty $
. This proves Proposition 2.9.
$k\to \infty $
. This proves Proposition 2.9.
Step 2. The higher derivatives. For a smooth function f defined on a neighborhood of a point x by
![]() $j^\ell _x(f)$
, we will denote its
$j^\ell _x(f)$
, we will denote its
![]() $\ell $
-jet at x. Below we prove the following proposition.
$\ell $
-jet at x. Below we prove the following proposition.
Proposition 2.12. In the conditions of Proposition 2.9, for every
![]() $\ell \in {\mathbb N}$
, the
$\ell \in {\mathbb N}$
, the
![]() $\ell $
-jet at
$\ell $
-jet at
![]() $x(k)$
of the difference
$x(k)$
of the difference
![]() $\widetilde {\phi }\circ \widetilde {F}^{N_k}-\phi $
tends to zero, as
$\widetilde {\phi }\circ \widetilde {F}^{N_k}-\phi $
tends to zero, as
![]() $k\to \infty $
.
$k\to \infty $
.
Proposition 2.12 will imply
![]() $C^{\infty }$
-smoothness and
$C^{\infty }$
-smoothness and
![]() $\phi $
-flatness of the extended function
$\phi $
-flatness of the extended function
![]() $\widetilde {\phi }$
at the points of the boundary interval
$\widetilde {\phi }$
at the points of the boundary interval
![]() $J\times \{0\}$
.
$J\times \{0\}$
.
For every
![]() $\ell \in {\mathbb N}$
and
$\ell \in {\mathbb N}$
and
![]() $x\in {\mathbb R}^2$
, let
$x\in {\mathbb R}^2$
, let
![]() $J^\ell _x$
denote the space of
$J^\ell _x$
denote the space of
![]() $\ell $
-jets of functions at the point x. The map
$\ell $
-jets of functions at the point x. The map
![]() $\widetilde {F}$
induces a transformation of functions,
$\widetilde {F}$
induces a transformation of functions,
![]() $g\mapsto g\circ \widetilde {F}$
. This induces linear operators in the jet spaces,
$g\mapsto g\circ \widetilde {F}$
. This induces linear operators in the jet spaces,
![]() $D_\ell \widetilde {F}(x):J^\ell _{\widetilde {F}(x)}\to J ^\ell _{x}$
. We identify the space of
$D_\ell \widetilde {F}(x):J^\ell _{\widetilde {F}(x)}\to J ^\ell _{x}$
. We identify the space of
![]() $\ell $
-jets at each point in
$\ell $
-jets at each point in
![]() ${\mathbb R}^2$
with the
${\mathbb R}^2$
with the
![]() $\ell $
-jet space at the origin, which, in its turn, is identified with the space
$\ell $
-jet space at the origin, which, in its turn, is identified with the space
![]() ${\mathcal P}_{\leq \ell }$
of polynomials in two variables of degrees no greater than
${\mathcal P}_{\leq \ell }$
of polynomials in two variables of degrees no greater than
![]() $\ell $
. Thus, we consider the operator
$\ell $
. Thus, we consider the operator
![]() $D_\ell \widetilde {F}(x)$
as acting on the above space
$D_\ell \widetilde {F}(x)$
as acting on the above space
![]() ${\mathcal P}_{\leq \ell }$
. One has
${\mathcal P}_{\leq \ell }$
. One has
Linear changes of variables
![]() $(\tau ,\phi )$
act on the space
$(\tau ,\phi )$
act on the space
![]() ${\mathcal P}_{\leq \ell }$
and induce an injective linear anti-representation
${\mathcal P}_{\leq \ell }$
and induce an injective linear anti-representation
![]() $\rho :{\operatorname {GL}} _2({\mathbb R})\to {\operatorname {GL}} ({\mathcal P}_{\leq \ell })$
. Let A denote the unipotent Jordan cell, see equation (2.19).
$\rho :{\operatorname {GL}} _2({\mathbb R})\to {\operatorname {GL}} ({\mathcal P}_{\leq \ell })$
. Let A denote the unipotent Jordan cell, see equation (2.19).
Proposition 2.13. For every sequence of points
![]() $x(k)=(\tau _{0k},\phi _{0k})\in W$
with
$x(k)=(\tau _{0k},\phi _{0k})\in W$
with
![]() $\phi _{0k}\to 0$
, as
$\phi _{0k}\to 0$
, as
![]() $k\to \infty $
, set
$k\to \infty $
, set
![]() $N_k:=N(x(k))$
, one has
$N_k:=N(x(k))$
, one has
Proof. One has
by equation (2.15). Set
![]() $x_j(k)=(\tau _{jk},\phi _{jk})=\widetilde {F}^j(x(k))$
,
$x_j(k)=(\tau _{jk},\phi _{jk})=\widetilde {F}^j(x(k))$
,
![]() $j=0,\ldots , N_k-1$
. One has
$j=0,\ldots , N_k-1$
. One has
by equation (2.26) and Proposition 2.6(c). We use equation (2.24) and the following multidimensional version of Proposition 2.11.
Proposition 2.14. Consider arbitrary sequences of numbers
![]() $\phi _{0k}>0$
,
$\phi _{0k}>0$
,
![]() $N_k\in {\mathbb N}$
,
$N_k\in {\mathbb N}$
,
![]() $\phi _{0k}\to 0$
,
$\phi _{0k}\to 0$
,
![]() $N_k=O(1/{\phi _{0k}})$
, as
$N_k=O(1/{\phi _{0k}})$
, as
![]() $k\to \infty $
, and matrix collections
$k\to \infty $
, and matrix collections
 $$ \begin{align} \mathcal M_k &=(M_{1;k},\ldots,M_{N_k;k}),\quad M_{j;k}\in{\operatorname{GL}} ({\mathcal P}_{\leq\ell}),\notag \\ M_{j;k} &=\rho(A)+o(\phi_{0k}^m)\quad \text{for every } m\in{\mathbb N};\quad A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1 \end{matrix}\bigg). \end{align} $$
$$ \begin{align} \mathcal M_k &=(M_{1;k},\ldots,M_{N_k;k}),\quad M_{j;k}\in{\operatorname{GL}} ({\mathcal P}_{\leq\ell}),\notag \\ M_{j;k} &=\rho(A)+o(\phi_{0k}^m)\quad \text{for every } m\in{\mathbb N};\quad A=\bigg(\begin{matrix} 1 & 1\\ 0 & 1 \end{matrix}\bigg). \end{align} $$
Here the latter asymptotics is uniform in
![]() $j=1,\ldots ,N_k$
for each individual m, as
$j=1,\ldots ,N_k$
for each individual m, as
![]() $k\to \infty $
. Then the product of the matrices
$k\to \infty $
. Then the product of the matrices
![]() $M_{j;k}$
has the asymptotics
$M_{j;k}$
has the asymptotics
Proof. Conjugating the matrices
![]() $M_{j;k}$
by
$M_{j;k}$
by
![]() $\rho (H_k)$
,
$\rho (H_k)$
,
![]() $H_k:={\operatorname {diag}} (1,\phi _{0k}^{-1})$
, transforms them to matrices
$H_k:={\operatorname {diag}} (1,\phi _{0k}^{-1})$
, transforms them to matrices
 $$ \begin{align*}\widetilde{M}_{j;k}=\rho(B_k)+o(\phi_{0k}^{m'}),\quad B_k=\bigg(\begin{matrix} 1 & \phi_{0k}\\ 0 & 1 \end{matrix}\bigg), \quad m'=m-\ell-1.\end{align*} $$
$$ \begin{align*}\widetilde{M}_{j;k}=\rho(B_k)+o(\phi_{0k}^{m'}),\quad B_k=\bigg(\begin{matrix} 1 & \phi_{0k}\\ 0 & 1 \end{matrix}\bigg), \quad m'=m-\ell-1.\end{align*} $$
It suffices to show that the product of the matrices
![]() $\widetilde {M}_{j;k}$
has asymptotics
$\widetilde {M}_{j;k}$
has asymptotics
![]() $\rho (B_k^{N_k})+o(\phi _{0k}^m)$
for every
$\rho (B_k^{N_k})+o(\phi _{0k}^m)$
for every
![]() $m\in {\mathbb N}$
, as in Claim 3. This is done by applying the arguments from the proof of Claim 3 to the left-invariant vector field on
$m\in {\mathbb N}$
, as in Claim 3. This is done by applying the arguments from the proof of Claim 3 to the left-invariant vector field on
![]() ${\operatorname {GL}} ({\mathcal P}_{\leq \ell })$
whose time t flow map acts by right multiplication by
${\operatorname {GL}} ({\mathcal P}_{\leq \ell })$
whose time t flow map acts by right multiplication by
![]() $\rho (A^t)$
.
$\rho (A^t)$
.
Equation (2.25) is deduced from Proposition 2.14 and equations (2.24), (2.27), as equation (2.23).
Proof of Proposition 2.12
The polynomial representing the
![]() $\ell $
-jet of the initial function
$\ell $
-jet of the initial function
![]() $\widetilde {\phi }$
at a point
$\widetilde {\phi }$
at a point
![]() $z\in \widehat \Delta $
tends to the linear polynomial
$z\in \widehat \Delta $
tends to the linear polynomial
![]() $P(\tau ,\phi )=\phi $
, as
$P(\tau ,\phi )=\phi $
, as
![]() $z\to 0$
, so that its distance to
$z\to 0$
, so that its distance to
![]() $P(\tau ,\phi )$
is
$P(\tau ,\phi )$
is
![]() $o(\phi ^m)$
for every
$o(\phi ^m)$
for every
![]() $m\in {\mathbb N}$
, by flatness of
$m\in {\mathbb N}$
, by flatness of
![]() $\widetilde {\phi }$
on
$\widetilde {\phi }$
on
![]() $\widehat \Delta $
. This together with Proposition 2.6(c) implies that the distance of its
$\widehat \Delta $
. This together with Proposition 2.6(c) implies that the distance of its
![]() $\ell $
-jet at the point
$\ell $
-jet at the point
![]() $\widetilde {F}^{N_k}(x(k))$
to the polynomial
$\widetilde {F}^{N_k}(x(k))$
to the polynomial
![]() $\phi $
is asymptotic to
$\phi $
is asymptotic to
![]() $o(\phi _{0k}^m)$
. The image of the latter
$o(\phi _{0k}^m)$
. The image of the latter
![]() $\ell $
-jet under the operator
$\ell $
-jet under the operator
![]() $D_\ell \widetilde {F}^{N_k}(x(k))$
is also
$D_\ell \widetilde {F}^{N_k}(x(k))$
is also
![]() $o(\phi _{0k}^m)$
-close to
$o(\phi _{0k}^m)$
-close to
![]() $\phi $
for every
$\phi $
for every
![]() $m\in {\mathbb N}$
. This follows from the previous statement, equation (2.25), the fact that
$m\in {\mathbb N}$
. This follows from the previous statement, equation (2.25), the fact that
![]() $\rho (A)$
fixes
$\rho (A)$
fixes
![]() $\phi $
and the asymptotics
$\phi $
and the asymptotics
![]() $N_k=O(\phi _{0k}^{-1})$
. Finally, we get that the difference of the
$N_k=O(\phi _{0k}^{-1})$
. Finally, we get that the difference of the
![]() $\ell $
-jet of the function
$\ell $
-jet of the function
![]() $\phi $
at
$\phi $
at
![]() $x(k)$
and the
$x(k)$
and the
![]() $\ell $
-jet
$\ell $
-jet
![]() $j^\ell _{x(k)}(\widetilde {\phi }\circ \widetilde {F}^{N_k})$
of the extended function tends to zero, as
$j^\ell _{x(k)}(\widetilde {\phi }\circ \widetilde {F}^{N_k})$
of the extended function tends to zero, as
![]() $k\to \infty $
. Proposition 2.12 is proved.
$k\to \infty $
. Proposition 2.12 is proved.
Lemma 2.8 follows from Proposition 2.12. It implies statement (1) of Theorem 1.30.
2.5 Normal form. Proof of statement (2) of Theorem 1.30
Let
![]() $\widetilde {\phi }$
be a function from statement (1) of Theorem 1.30. The vector function
$\widetilde {\phi }$
be a function from statement (1) of Theorem 1.30. The vector function
![]() $(\tau ,\widetilde {\phi })$
has non-degenerate Jacobian matrix at J. Hence, shrinking W, we can and will consider that
$(\tau ,\widetilde {\phi })$
has non-degenerate Jacobian matrix at J. Hence, shrinking W, we can and will consider that
![]() $(\tau ,\widetilde {\phi })$
are
$(\tau ,\widetilde {\phi })$
are
![]() $C^{\infty }$
-smooth coordinates on
$C^{\infty }$
-smooth coordinates on
![]() $W\cup J$
. In these coordinates,
$W\cup J$
. In these coordinates,
Claim 4. Shrinking W, one can achieve that there exists a
![]() $C^{\infty }$
-smooth function
$C^{\infty }$
-smooth function
![]() $\widetilde {\tau }(\tau ,\widetilde {\phi })=\tau +{\operatorname {flat}}(\widetilde {\phi })$
on
$\widetilde {\tau }(\tau ,\widetilde {\phi })=\tau +{\operatorname {flat}}(\widetilde {\phi })$
on
![]() $W\cup J$
such that
$W\cup J$
such that
![]() $(\widetilde {\tau },\widetilde {\phi })$
are
$(\widetilde {\tau },\widetilde {\phi })$
are
![]() $C^{\infty }$
-smooth coordinates on
$C^{\infty }$
-smooth coordinates on
![]() $W\cup J$
in which
$W\cup J$
in which
![]() $\widetilde {F}$
acts as in equation (1.14):
$\widetilde {F}$
acts as in equation (1.14):
Proof. Equation (2.31) is equivalent to the equation
Shifting
![]() $\tau $
and shrinking W, we can and will consider that
$\tau $
and shrinking W, we can and will consider that
![]() $(0,0)\in J$
,
$(0,0)\in J$
,
Fix a small
![]() $\chi \in (0,\tfrac 12)$
and a
$\chi \in (0,\tfrac 12)$
and a
![]() $\eta>0$
(depending on
$\eta>0$
(depending on
![]() $\chi $
) satisfying the statements of Proposition 2.2 and such that the second statement (set equality) in equation (2.33) holds for every
$\chi $
) satisfying the statements of Proposition 2.2 and such that the second statement (set equality) in equation (2.33) holds for every
![]() $\zeta <3\eta $
. Consider the sector
$\zeta <3\eta $
. Consider the sector
![]() $S_{\chi ,\eta }$
, the segment
$S_{\chi ,\eta }$
, the segment
![]() $K=\{0\}\times [0, \eta /2]$
, and the fundamental domain
$K=\{0\}\times [0, \eta /2]$
, and the fundamental domain
![]() $\Delta $
bounded by K,
$\Delta $
bounded by K,
![]() $F(K)$
, and the (now horizontal) straightline segment connecting their endpoints distinct from the origin. Set
$F(K)$
, and the (now horizontal) straightline segment connecting their endpoints distinct from the origin. Set
![]() $\widehat \Delta :=\overline \Delta \setminus \{(0,0)\}\subset S_{\chi ,\eta }$
. First, we define the function
$\widehat \Delta :=\overline \Delta \setminus \{(0,0)\}\subset S_{\chi ,\eta }$
. First, we define the function
![]() $\widetilde {\tau }$
on the sector
$\widetilde {\tau }$
on the sector
![]() $S_{\chi ,\eta }$
so that equation (2.32) holds, whenever
$S_{\chi ,\eta }$
so that equation (2.32) holds, whenever
![]() $x, \widetilde {F}(x)\in S_{\chi ,\eta }$
. Afterward, we extend
$x, \widetilde {F}(x)\in S_{\chi ,\eta }$
. Afterward, we extend
![]() $\widetilde {\tau }$
to all of W by dynamics.
$\widetilde {\tau }$
to all of W by dynamics.
Fix a
![]() $\sigma \in (0,\tfrac 12(\tfrac 12-\chi ))$
. Let
$\sigma \in (0,\tfrac 12(\tfrac 12-\chi ))$
. Let
![]() $\rho _1$
,
$\rho _1$
,
![]() $\rho _2$
be a partition of unity on the interval
$\rho _2$
be a partition of unity on the interval
![]() $(-\chi , 1+\chi )$
subordinated to its covering by intervals
$(-\chi , 1+\chi )$
subordinated to its covering by intervals
![]() $(-\chi ,\tfrac 12+\sigma )$
,
$(-\chi ,\tfrac 12+\sigma )$
,
![]() $(\tfrac 12-\sigma ,1+\chi )$
, see equation (2.13). Set
$(\tfrac 12-\sigma ,1+\chi )$
, see equation (2.13). Set
![]() $\nu := {\tau }/{\widetilde {\phi }}$
. For every
$\nu := {\tau }/{\widetilde {\phi }}$
. For every
![]() $x\in S_{\chi ,\eta }$
, set
$x\in S_{\chi ,\eta }$
, set
The inclusion
![]() $x, \widetilde {F}(x)\in S_{\chi ,\eta }$
implies equation (2.32), whenever
$x, \widetilde {F}(x)\in S_{\chi ,\eta }$
implies equation (2.32), whenever
![]() $\eta $
is small enough, since then
$\eta $
is small enough, since then
![]() $\rho _1(\nu (x))=1$
and
$\rho _1(\nu (x))=1$
and
![]() $\rho _2(\nu \circ F(x))=1$
, as in the proof of Proposition 2.2, and by equation (2.34) and
$\rho _2(\nu \circ F(x))=1$
, as in the proof of Proposition 2.2, and by equation (2.34) and
![]() $\widetilde {F}$
-invariance of the function
$\widetilde {F}$
-invariance of the function
![]() $\widetilde {\phi }$
. Recall that the height of the fundamental domain
$\widetilde {\phi }$
. Recall that the height of the fundamental domain
![]() $\Delta $
is
$\Delta $
is
![]() $\eta /2$
. Let us now replace W by
$\eta /2$
. Let us now replace W by
![]() $W\cap \{\widetilde {\phi }< (\eta /2)\}$
. Then for every
$W\cap \{\widetilde {\phi }< (\eta /2)\}$
. Then for every
![]() $x\in W$
, there exists a
$x\in W$
, there exists a
![]() $N=N(x)\in {\mathbb Z}$
such that
$N=N(x)\in {\mathbb Z}$
such that
![]() $\widetilde {F}^N(x)\in \widehat \Delta $
; the latter N is unique, unless
$\widetilde {F}^N(x)\in \widehat \Delta $
; the latter N is unique, unless
![]() $\widetilde {F}^N(x)\in \partial \widehat \Delta $
. This follows from equation (2.33). Set
$\widetilde {F}^N(x)\in \partial \widehat \Delta $
. This follows from equation (2.33). Set
The function
![]() $\widetilde {\tau }(x)$
is well defined and
$\widetilde {\tau }(x)$
is well defined and
![]() $C^\infty $
-smooth on all of W and satisfies equation (2.32) there. Indeed, it suffices to check smoothness on the boundary
$C^\infty $
-smooth on all of W and satisfies equation (2.32) there. Indeed, it suffices to check smoothness on the boundary
![]() $\partial \widehat \Delta $
and on its images. If
$\partial \widehat \Delta $
and on its images. If
![]() $x\in \partial \widehat \Delta $
, then either
$x\in \partial \widehat \Delta $
, then either
![]() $x, \widetilde {F}(x)\in \widehat \Delta $
or
$x, \widetilde {F}(x)\in \widehat \Delta $
or
![]() $x, \widetilde {F}^{-1}(x)\in \widehat \Delta $
. In the first case, one can take
$x, \widetilde {F}^{-1}(x)\in \widehat \Delta $
. In the first case, one can take
![]() $N=0$
or
$N=0$
or
![]() $N=1$
. For both these values of N, the corresponding right-hand sides
$N=1$
. For both these values of N, the corresponding right-hand sides
![]() $\widetilde {\tau }(x)$
and
$\widetilde {\tau }(x)$
and
![]() $\widetilde {\tau }\circ F(x)-\widetilde {\phi }(x)$
in equation (2.35) coincide, since equation (2.32) holds on
$\widetilde {\tau }\circ F(x)-\widetilde {\phi }(x)$
in equation (2.35) coincide, since equation (2.32) holds on
![]() $S_{\chi ,\eta }\supset \widehat \Delta $
. The second case is treated analogously. For the same reason, the function
$S_{\chi ,\eta }\supset \widehat \Delta $
. The second case is treated analogously. For the same reason, the function
![]() $\widetilde {\tau }$
on
$\widetilde {\tau }$
on
![]() $S_{\chi ,\eta }$
given by equation (2.34) coincides with the corresponding expression in equation (2.35) (in which
$S_{\chi ,\eta }$
given by equation (2.34) coincides with the corresponding expression in equation (2.35) (in which
![]() $N\in \{0,\pm 1\}$
). This implies smoothness of the function in equation (2.35) on a neighborhood of the subset
$N\in \{0,\pm 1\}$
). This implies smoothness of the function in equation (2.35) on a neighborhood of the subset
![]() $\widehat \Delta \subset W$
. One has
$\widehat \Delta \subset W$
. One has
![]() $\widetilde {\tau }(\widetilde {F}(x))=\widetilde {\tau }(x)+\widetilde {\phi }(x)$
, by equation (2.35). This together with the above discussion implies that
$\widetilde {\tau }(\widetilde {F}(x))=\widetilde {\tau }(x)+\widetilde {\phi }(x)$
, by equation (2.35). This together with the above discussion implies that
![]() $\widetilde {\tau }$
is
$\widetilde {\tau }$
is
![]() $C^\infty $
-smooth on W and satisfies equation (2.32) on all of W. The function
$C^\infty $
-smooth on W and satisfies equation (2.32) on all of W. The function
![]() $\widetilde {\tau }$
extends to a
$\widetilde {\tau }$
extends to a
![]() $C^\infty $
-smooth function on
$C^\infty $
-smooth function on
![]() $W\cup J$
, and the function
$W\cup J$
, and the function
![]() $\widetilde {\tau }-\tau $
is
$\widetilde {\tau }-\tau $
is
![]() $\widetilde {\phi }$
-flat. This is proved as in §2.4. Namely, first it is
$\widetilde {\phi }$
-flat. This is proved as in §2.4. Namely, first it is
![]() $\widetilde {\phi }$
-flat on
$\widetilde {\phi }$
-flat on
![]() $S_{\chi ,\eta }$
, as in Proposition 2.3. Then we fix an arbitrary compact segment
$S_{\chi ,\eta }$
, as in Proposition 2.3. Then we fix an arbitrary compact segment
![]() $[a',b']\subset (a,b)=J$
. The differential of the map
$[a',b']\subset (a,b)=J$
. The differential of the map
![]() $H:(\tau ,\widetilde {\phi })\mapsto (\widetilde {\tau },\widetilde {\phi })$
tends to the identity, and all its higher derivatives tend to zero, as
$H:(\tau ,\widetilde {\phi })\mapsto (\widetilde {\tau },\widetilde {\phi })$
tends to the identity, and all its higher derivatives tend to zero, as
![]() $\widetilde {\phi }\to 0$
, uniformly in
$\widetilde {\phi }\to 0$
, uniformly in
![]() $\tau \in [a',b']$
. In particular,
$\tau \in [a',b']$
. In particular,
![]() ${{\partial \widetilde {\tau }}(\tau ,\widetilde {\phi })/{\partial \tau }\to 1}$
. Indeed, for every
${{\partial \widetilde {\tau }}(\tau ,\widetilde {\phi })/{\partial \tau }\to 1}$
. Indeed, for every
![]() $x\in W$
, set
$x\in W$
, set
![]() $N=N(x)$
, one has
$N=N(x)$
, one has
![]() $H(\tau ,\widetilde {\phi })=(\widetilde {\tau }\circ \widetilde {F}^N(\tau ,\widetilde {\phi })-N\widetilde {\phi },\ \widetilde {\phi })$
on a neighborhood of x. This together with equations (2.23) and (2.25) applied to the differential and higher jet action of the iterates of the map
$H(\tau ,\widetilde {\phi })=(\widetilde {\tau }\circ \widetilde {F}^N(\tau ,\widetilde {\phi })-N\widetilde {\phi },\ \widetilde {\phi })$
on a neighborhood of x. This together with equations (2.23) and (2.25) applied to the differential and higher jet action of the iterates of the map
![]() $\widetilde {F}$
imply the above convergence statement. The restriction of the function
$\widetilde {F}$
imply the above convergence statement. The restriction of the function
![]() $\widetilde {\tau }$
to
$\widetilde {\tau }$
to
![]() $S_{\chi ,\eta }$
extends continuously to the origin as
$S_{\chi ,\eta }$
extends continuously to the origin as
![]() $\widetilde {\tau }(0,0)=0$
. Thus,
$\widetilde {\tau }(0,0)=0$
. Thus,
![]() $\widetilde {\tau }(0,\widetilde {\phi })\to 0$
, as
$\widetilde {\tau }(0,\widetilde {\phi })\to 0$
, as
![]() $\widetilde {\phi }\to 0$
. This together with uniform convergence
$\widetilde {\phi }\to 0$
. This together with uniform convergence
![]() ${\partial \widetilde {\tau }}(\tau ,\widetilde {\phi })/{\partial \tau }\to 1$
in
${\partial \widetilde {\tau }}(\tau ,\widetilde {\phi })/{\partial \tau }\to 1$
in
![]() $\tau \in [a',b']$
, as
$\tau \in [a',b']$
, as
![]() $\widetilde {\phi }\to 0$
, implies uniform convergence
$\widetilde {\phi }\to 0$
, implies uniform convergence
![]() $\widetilde {\tau }(\tau ,\widetilde {\phi })\to \tau $
. Together with the above higher derivative convergence, this implies
$\widetilde {\tau }(\tau ,\widetilde {\phi })\to \tau $
. Together with the above higher derivative convergence, this implies
![]() $\widetilde {\phi }$
-flatness of the function
$\widetilde {\phi }$
-flatness of the function
![]() $\widetilde {\tau }-\tau $
and proves the claim.
$\widetilde {\tau }-\tau $
and proves the claim.
The above claim immediately implies statement (2) of Theorem 1.30.
2.6 Proof of existence in Theorem 1.26. Proof of Theorem 1.27
Let F be a
![]() $C^{\infty }$
-lifted strongly billiard-like map. Let
$C^{\infty }$
-lifted strongly billiard-like map. Let
![]() $(\tau ,h)$
be the coordinates from Theorem 2.1. Set
$(\tau ,h)$
be the coordinates from Theorem 2.1. Set
![]() $\phi =\sqrt h$
. Let
$\phi =\sqrt h$
. Let
![]() $\widetilde {F}$
denote the map F written in the coordinates
$\widetilde {F}$
denote the map F written in the coordinates
![]() $(\tau ,\phi )$
, which is
$(\tau ,\phi )$
, which is
![]() $C^{\infty }$
-smooth and takes the form
$C^{\infty }$
-smooth and takes the form
![]() $(\tau ,\phi )\mapsto (\tau +\phi +{\operatorname {flat}}(\phi ), \phi +{\operatorname {flat}}(\phi ))$
(Theorem 2.1). There exists a
$(\tau ,\phi )\mapsto (\tau +\phi +{\operatorname {flat}}(\phi ), \phi +{\operatorname {flat}}(\phi ))$
(Theorem 2.1). There exists a
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
![]() $\widetilde {\phi }=\phi +{\operatorname {flat}}(\phi )$
(Theorem 1.30). The function
$\widetilde {\phi }=\phi +{\operatorname {flat}}(\phi )$
(Theorem 1.30). The function
![]() $\widetilde {h}:=\widetilde {\phi }^2$
is F-invariant,
$\widetilde {h}:=\widetilde {\phi }^2$
is F-invariant,
![]() $C^{\infty }$
-smooth, and
$C^{\infty }$
-smooth, and
![]() $\widetilde {h}=h+{\operatorname {flat}}(h)$
; hence,
$\widetilde {h}=h+{\operatorname {flat}}(h)$
; hence,
![]() $({\partial \widetilde {h}}/{\partial h})> 0$
on J and on some domain adjacent to J. The existence in Theorem 1.26 is proved. Non-uniqueness of the function
$({\partial \widetilde {h}}/{\partial h})> 0$
on J and on some domain adjacent to J. The existence in Theorem 1.26 is proved. Non-uniqueness of the function
![]() $\widetilde {h}$
will be proved in §2.9.
$\widetilde {h}$
will be proved in §2.9.
Let us now prove Theorem 1.27. Let us fix a function
![]() $\widetilde {h}$
constructed above. Let
$\widetilde {h}$
constructed above. Let
![]() $\theta $
denote the time function of the Hamiltonian vector field with the Hamiltonian function
$\theta $
denote the time function of the Hamiltonian vector field with the Hamiltonian function
![]() $\widetilde {h}$
normalized to vanish on the vertical axis
$\widetilde {h}$
normalized to vanish on the vertical axis
![]() $\{\tau =0\}$
. (We consider that
$\{\tau =0\}$
. (We consider that
![]() $(0,0)\in J$
, shifting the coordinate
$(0,0)\in J$
, shifting the coordinate
![]() $\tau $
.) The coordinates
$\tau $
.) The coordinates
![]() $(\theta ,\widetilde {h})$
are symplectic. In these coordinates,
$(\theta ,\widetilde {h})$
are symplectic. In these coordinates,
![]() $F(\theta ,\widetilde {h})=(\theta +\xi (\widetilde {h}), \widetilde {h})$
for some function
$F(\theta ,\widetilde {h})=(\theta +\xi (\widetilde {h}), \widetilde {h})$
for some function
![]() $\xi (\widetilde {h})=\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}}\psi (\widetilde {h})$
in one variable, since F preserves the symplectic area;
$\xi (\widetilde {h})=\sqrt {\vphantom{\widetilde {h^A}}\widetilde {h}}\psi (\widetilde {h})$
in one variable, since F preserves the symplectic area;
![]() $\psi $
is
$\psi $
is
![]() $C^\infty $
-smooth and
$C^\infty $
-smooth and
![]() $\psi (0)>0$
, as in Claim 1 in §2.1. Afterward, modifying the functions
$\psi (0)>0$
, as in Claim 1 in §2.1. Afterward, modifying the functions
![]() $\widetilde {h}$
and
$\widetilde {h}$
and
![]() $\theta $
, as at the end of §2.1, we get new coordinates
$\theta $
, as at the end of §2.1, we get new coordinates
![]() $(\tau ,\widetilde {h})$
(with new
$(\tau ,\widetilde {h})$
(with new
![]() $\tau $
) in which F takes the form in equation (1.12). Theorem 1.27 is proved.
$\tau $
) in which F takes the form in equation (1.12). Theorem 1.27 is proved.
2.7 Foliation by caustics. Proof of existence in Theorems 1.9, 1.12, and 1.13
First, let us consider the case when
![]() $\gamma $
is an unbounded submanifold: a strictly convex curve injectively parameterized by interval and bounding a domain in
$\gamma $
is an unbounded submanifold: a strictly convex curve injectively parameterized by interval and bounding a domain in
![]() ${\mathbb R}^2$
(conditions of statement (1) of Theorem 1.9).
${\mathbb R}^2$
(conditions of statement (1) of Theorem 1.9).
Let W denote the domain in the space of oriented lines that consists of lines intersecting
![]() $\gamma $
twice and satisfying condition (b) from the beginning of §1.3. Let
$\gamma $
twice and satisfying condition (b) from the beginning of §1.3. Let
![]() $\widehat {\gamma }$
denote the curve given by the family of orienting tangent lines of
$\widehat {\gamma }$
denote the curve given by the family of orienting tangent lines of
![]() $\gamma $
. The domain W is adjacent to
$\gamma $
. The domain W is adjacent to
![]() $\widehat {\gamma }$
. The billiard ball map is well defined on
$\widehat {\gamma }$
. The billiard ball map is well defined on
![]() $W\cup \widehat {\gamma }$
. Each line L close to a tangent line
$W\cup \widehat {\gamma }$
. Each line L close to a tangent line
![]() $\ell $
of
$\ell $
of
![]() $\gamma $
carries a canonical orientation: the pullback of the orientation of the line
$\gamma $
carries a canonical orientation: the pullback of the orientation of the line
![]() $\ell $
under a projection
$\ell $
under a projection
![]() $L\to \ell $
close to identity. The billiard ball map acting on thus oriented lines close to tangent lines of
$L\to \ell $
close to identity. The billiard ball map acting on thus oriented lines close to tangent lines of
![]() $\gamma $
and intersecting
$\gamma $
and intersecting
![]() $\gamma $
twice will be treated as a map acting on non-oriented lines: we will just forget the orientation.
$\gamma $
twice will be treated as a map acting on non-oriented lines: we will just forget the orientation.
Let us fix a natural length parameter s on the curve
![]() $\gamma $
that orients
$\gamma $
that orients
![]() $\gamma $
counterclockwise, that is, positively as the boundary of its convex side. Let us identify each point in
$\gamma $
counterclockwise, that is, positively as the boundary of its convex side. Let us identify each point in
![]() $\gamma $
with the corresponding length parameter value. Let us introduce the following tuples of coordinates on the domain W. For every line
$\gamma $
with the corresponding length parameter value. Let us introduce the following tuples of coordinates on the domain W. For every line
![]() $L\in W$
, let
$L\in W$
, let
![]() $s_1=s_1(L)$
and
$s_1=s_1(L)$
and
![]() $s_2=s_2(L)$
denote the length parameter values of its intersection points with
$s_2=s_2(L)$
denote the length parameter values of its intersection points with
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\phi _j$
denote the oriented angles between L and the tangent lines to
$\phi _j$
denote the oriented angles between L and the tangent lines to
![]() $\gamma $
at the points
$\gamma $
at the points
![]() $s_j$
. To each L, we put into correspondence the pair
$s_j$
. To each L, we put into correspondence the pair
![]() $(s_1,\phi _1)$
, where
$(s_1,\phi _1)$
, where
![]() $s_j$
are numerated so that
$s_j$
are numerated so that
![]() $s_1<s_2$
. Set
$s_1<s_2$
. Set
see equation (1.2). Any of the pairs
![]() $(s_1,\phi _1)$
or
$(s_1,\phi _1)$
or
![]() $(s_1,y_1)$
defines L uniquely. Recall that
$(s_1,y_1)$
defines L uniquely. Recall that
![]() $(s_1,y_1)$
are symplectic coordinates on W, see the discussion after Remark 1.18. Let
$(s_1,y_1)$
are symplectic coordinates on W, see the discussion after Remark 1.18. Let
![]() ${V\subset {\mathbb R}\times {\mathbb R}_+}$
denote the domain W represented in the coordinates
${V\subset {\mathbb R}\times {\mathbb R}_+}$
denote the domain W represented in the coordinates
![]() $(s_1,y_1)$
. It is adjacent to an interval
$(s_1,y_1)$
. It is adjacent to an interval
![]() $J=(a,b)\times \{0\}$
representing
$J=(a,b)\times \{0\}$
representing
![]() $\widehat {\gamma }$
. Let
$\widehat {\gamma }$
. Let
![]() $\widetilde {V}\subset {\mathbb R}\times {\mathbb R}_+$
denote the same domain represented in the coordinates
$\widetilde {V}\subset {\mathbb R}\times {\mathbb R}_+$
denote the same domain represented in the coordinates
![]() $(s_1,\phi _1)$
.
$(s_1,\phi _1)$
.
Proposition 2.15. In the coordinates
![]() $(s_1,y_1)$
, the billiard ball map is a
$(s_1,y_1)$
, the billiard ball map is a
![]() $C^{\infty }$
-lifted strongly billiard-like map F defined on
$C^{\infty }$
-lifted strongly billiard-like map F defined on
![]() $V\cup J$
. In the coordinates
$V\cup J$
. In the coordinates
![]() $(s_1,\phi _1)$
, it is a
$(s_1,\phi _1)$
, it is a
![]() $C^{\infty }$
-smooth diffeomorphism
$C^{\infty }$
-smooth diffeomorphism
![]() $\widetilde {F}$
defined on
$\widetilde {F}$
defined on
![]() $\widetilde {V}\cup J$
.
$\widetilde {V}\cup J$
.
Proposition 2.16. Shrinking V (without changing its boundary interval J), one can achieve that there exists a
![]() $C^{\infty }$
-smooth F-invariant function
$C^{\infty }$
-smooth F-invariant function
![]() $G(s_1,y_1)$
on
$G(s_1,y_1)$
on
![]() $V\cup J$
such that
$V\cup J$
such that
Proof. The proposition follows from Theorem 1.26 (existence).
From now on, by W, we denote the domain of those lines that are represented by points of the (shrinked) domain V from Proposition 2.16.
The level curves of the function G are F-invariant and form a
![]() $C^\infty $
-smooth foliation. Lifting everything to the domain W in the space of lines, we get a foliation by invariant curves under the billiard ball map. Each leaf is a smooth family of lines. Its enveloping curve is a caustic of the billiard in
$C^\infty $
-smooth foliation. Lifting everything to the domain W in the space of lines, we get a foliation by invariant curves under the billiard ball map. Each leaf is a smooth family of lines. Its enveloping curve is a caustic of the billiard in
![]() $\gamma $
. To prove that
$\gamma $
. To prove that
![]() $\gamma $
and the caustics in question form a
$\gamma $
and the caustics in question form a
![]() $C^{\infty }$
-smooth foliation of a domain adjacent to
$C^{\infty }$
-smooth foliation of a domain adjacent to
![]() $\gamma $
, we use the following lemma.
$\gamma $
, we use the following lemma.
Lemma 2.17. The above function G is
![]() $C^{\infty }$
-smooth as a function on the domain with boundary
$C^{\infty }$
-smooth as a function on the domain with boundary
![]() $W\cup \widehat {\gamma }$
in the space of lines. It has non-zero differential on
$W\cup \widehat {\gamma }$
in the space of lines. It has non-zero differential on
![]() $W\cup \widehat {\gamma }$
. Thus, its level curves form a
$W\cup \widehat {\gamma }$
. Thus, its level curves form a
![]() $C^{\infty }$
-smooth foliation of
$C^{\infty }$
-smooth foliation of
![]() $W\cup \widehat {\gamma }$
with
$W\cup \widehat {\gamma }$
with
![]() $\widehat {\gamma }$
being a leaf.
$\widehat {\gamma }$
being a leaf.
Remark 2.18. The function
![]() $s_1(L)$
is smooth on W but not on
$s_1(L)$
is smooth on W but not on
![]() $W\cup \widehat {\gamma }$
: it is not
$W\cup \widehat {\gamma }$
: it is not
![]() $C^1$
-smooth at points of the curve
$C^1$
-smooth at points of the curve
![]() $\widehat {\gamma }$
. Therefore, a priori, a function smooth in
$\widehat {\gamma }$
. Therefore, a priori, a function smooth in
![]() $(s_1,y_1)$
is not necessarily smooth on
$(s_1,y_1)$
is not necessarily smooth on
![]() $W\cup \widehat {\gamma }$
.
$W\cup \widehat {\gamma }$
.
Proof of Lemma 2.17
The function G is
![]() $C^\infty $
-smooth on W and has non-degenerate differential there, by Proposition 2.16. Let us prove that this also holds at points of the boundary curve
$C^\infty $
-smooth on W and has non-degenerate differential there, by Proposition 2.16. Let us prove that this also holds at points of the boundary curve
![]() $\widehat {\gamma }$
. The function G lifts to an
$\widehat {\gamma }$
. The function G lifts to an
![]() $\widetilde {F}$
-invariant function
$\widetilde {F}$
-invariant function
The map
![]() $(s_1,\phi _1)\to (s_1,s_2)$
is a diffeomorphism defined on
$(s_1,\phi _1)\to (s_1,s_2)$
is a diffeomorphism defined on
![]() $\widetilde {V}\cup J$
. The analogous statement holds for the diffeomorphism
$\widetilde {V}\cup J$
. The analogous statement holds for the diffeomorphism
![]() $(s_2,\phi _2)\mapsto (s_1,s_2)$
. One has
$(s_2,\phi _2)\mapsto (s_1,s_2)$
. One has
by invariance of the function
![]() $\widetilde {G}$
under sign change at the second coordinate and by its invariance under the billiard ball map represented by
$\widetilde {G}$
under sign change at the second coordinate and by its invariance under the billiard ball map represented by
![]() $\widetilde {\delta }_+:(s_1,\phi _1)\mapsto (s_2,-\phi _2)$
. Given an unordered pair
$\widetilde {\delta }_+:(s_1,\phi _1)\mapsto (s_2,-\phi _2)$
. Given an unordered pair
![]() $(s_1,s_2)$
, the tuples
$(s_1,s_2)$
, the tuples
![]() $(s_1,\phi _1)$
and
$(s_1,\phi _1)$
and
![]() $(s_2,\phi _2)$
are well defined up to permutation. Therefore, in the coordinates
$(s_2,\phi _2)$
are well defined up to permutation. Therefore, in the coordinates
![]() $(s_1,s_2)$
on
$(s_1,s_2)$
on
![]() $\widetilde {V}$
(where
$\widetilde {V}$
(where
![]() $a<s_1\leq s_2<b$
by definition), the function
$a<s_1\leq s_2<b$
by definition), the function
![]() $\widetilde {G}$
is
$\widetilde {G}$
is
![]() $C^\infty $
-smooth and extends
$C^\infty $
-smooth and extends
![]() $C^\infty $
-smoothly to a neighborhood of the diagonal (identified with J) in
$C^\infty $
-smoothly to a neighborhood of the diagonal (identified with J) in
![]() $(a,b)\times (a,b)$
as a function invariant under coordinate permutation. This means that in the coordinates
$(a,b)\times (a,b)$
as a function invariant under coordinate permutation. This means that in the coordinates
 $$ \begin{align*} (\alpha,\beta):=\bigg(\frac{s_1+s_2}2, \frac{s_2-s_1}2\bigg) \end{align*} $$
$$ \begin{align*} (\alpha,\beta):=\bigg(\frac{s_1+s_2}2, \frac{s_2-s_1}2\bigg) \end{align*} $$
(which are
![]() $C^{\infty }$
-diffeomorphic coordinates on
$C^{\infty }$
-diffeomorphic coordinates on
![]() $\widetilde {V}\cup J$
), the function
$\widetilde {V}\cup J$
), the function
![]() $\widetilde {G}$
is invariant under sign change at
$\widetilde {G}$
is invariant under sign change at
![]() $\beta $
. Hence,
$\beta $
. Hence,
![]() $\widetilde {G}$
is a
$\widetilde {G}$
is a
![]() $C^\infty $
-smooth function in
$C^\infty $
-smooth function in
![]() $(\alpha ,\beta ^2)$
,
$(\alpha ,\beta ^2)$
,
the function
![]() $\widehat G$
is
$\widehat G$
is
![]() $C^\infty $
-smooth on the domain in
$C^\infty $
-smooth on the domain in
![]() ${\mathbb R}_\alpha \times ({\mathbb R}_+)_\psi $
adjacent to J and corresponding to W, and it is also smooth at points of the boundary J.
${\mathbb R}_\alpha \times ({\mathbb R}_+)_\psi $
adjacent to J and corresponding to W, and it is also smooth at points of the boundary J.
Proposition 2.19. The pair
![]() $(\alpha ,\psi )$
forms
$(\alpha ,\psi )$
forms
![]() $C^{\infty }$
-smooth coordinates on the domain with boundary arc
$C^{\infty }$
-smooth coordinates on the domain with boundary arc
![]() $W\cup \widehat {\gamma }$
in the space of lines.
$W\cup \widehat {\gamma }$
in the space of lines.
Proof. Consider the map
![]() $S{\Lambda } : (s_1,s_2)\to \{\text {lines}\}$
sending a pair of points
$S{\Lambda } : (s_1,s_2)\to \{\text {lines}\}$
sending a pair of points
![]() $(s_1,s_2)$
of the curve
$(s_1,s_2)$
of the curve
![]() $\gamma $
to the line through them. (For
$\gamma $
to the line through them. (For
![]() $s_1=s_2=s$
, the image is the tangent line to
$s_1=s_2=s$
, the image is the tangent line to
![]() $\gamma $
at s.) The map
$\gamma $
at s.) The map
![]() $S{\Lambda } $
is
$S{\Lambda } $
is
![]() $C^{\infty }$
-smooth on
$C^{\infty }$
-smooth on
![]() $(a,b)\times (a,b)$
. It is invariant under permutation of the coordinates
$(a,b)\times (a,b)$
. It is invariant under permutation of the coordinates
![]() $s_1$
,
$s_1$
,
![]() $s_2$
, and its restriction to each connected component of the complement to the diagonal is a diffeomorphism, by convexity. Equivalently, it is
$s_2$
, and its restriction to each connected component of the complement to the diagonal is a diffeomorphism, by convexity. Equivalently, it is
![]() $C^{\infty }$
-smooth in the coordinates
$C^{\infty }$
-smooth in the coordinates
![]() $(\alpha ,\beta )$
and invariant under sign change at
$(\alpha ,\beta )$
and invariant under sign change at
![]() $\beta $
. Hence, it is smooth in
$\beta $
. Hence, it is smooth in
![]() $(\alpha ,\psi )$
. Its differential is non-degenerate at those points, where
$(\alpha ,\psi )$
. Its differential is non-degenerate at those points, where
![]() $s_1\neq s_2$
, or equivalently,
$s_1\neq s_2$
, or equivalently,
![]() $\psi \neq 0$
. It remains to check that it has non-degenerate differential at the points of the line
$\psi \neq 0$
. It remains to check that it has non-degenerate differential at the points of the line
![]() $\{\psi =0\}$
. To do this, consider yet another tuple of coordinates
$\{\psi =0\}$
. To do this, consider yet another tuple of coordinates
![]() $(\alpha ^*,\psi ^*)$
on
$(\alpha ^*,\psi ^*)$
on
![]() $W\cup \widehat {\gamma }$
defined as follows: for every
$W\cup \widehat {\gamma }$
defined as follows: for every
![]() $L\in W\cup \widehat {\gamma }$
:
$L\in W\cup \widehat {\gamma }$
:
-
• the point
 $\alpha ^*=\alpha ^*(L)\in (a,b)$
is the unique point in the curve
$\alpha ^*=\alpha ^*(L)\in (a,b)$
is the unique point in the curve
 $\gamma $
where the tangent line to
$\gamma $
where the tangent line to
 $\gamma $
is parallel to L (it exists by Rolle theorem);
$\gamma $
is parallel to L (it exists by Rolle theorem); -
• the number
 $\psi ^*=\psi ^*(L)$
is the distance between the line L and the above tangent line.
$\psi ^*=\psi ^*(L)$
is the distance between the line L and the above tangent line.
Proposition 2.20. The coordinates
![]() $(\alpha ^*,\psi ^*)$
are
$(\alpha ^*,\psi ^*)$
are
![]() $C^{\infty }$
-smooth coordinates on
$C^{\infty }$
-smooth coordinates on
![]() $W\cup \widehat {\gamma }$
.
$W\cup \widehat {\gamma }$
.
Proposition 2.20 follows from definition and strict convexity of
![]() $\gamma $
.
$\gamma $
.
Consider now
![]() $(\alpha ^*,\psi ^*)$
as functions of
$(\alpha ^*,\psi ^*)$
as functions of
![]() $(\alpha ,\psi )$
. One obviously has
$(\alpha ,\psi )$
. One obviously has
As
![]() $(\alpha ,\psi )\to (\alpha _0,0)$
, one has
$(\alpha ,\psi )\to (\alpha _0,0)$
, one has
Here
![]() $\kappa $
is the curvature of the curve
$\kappa $
is the curvature of the curve
![]() $\gamma $
. Indeed, as
$\gamma $
. Indeed, as
![]() $s_1,s_2\to \alpha _0$
, the line L through
$s_1,s_2\to \alpha _0$
, the line L through
![]() $s_1$
and
$s_1$
and
![]() $s_2$
is parallel to a line tangent to
$s_2$
is parallel to a line tangent to
![]() $\gamma $
at a point
$\gamma $
at a point
![]() $\alpha ^*$
that is
$\alpha ^*$
that is
![]() $o(s_1-s_2)$
-close to
$o(s_1-s_2)$
-close to
![]() $\alpha = ({s_1+s_2})/2$
. The distance between the two lines is asymptotic to
$\alpha = ({s_1+s_2})/2$
. The distance between the two lines is asymptotic to
![]() $\tfrac 12\kappa (\alpha )(\alpha ^*-s_1)^2$
, by [Reference Glutsyuk10, equation (2.1)]. This together with the equality
$\tfrac 12\kappa (\alpha )(\alpha ^*-s_1)^2$
, by [Reference Glutsyuk10, equation (2.1)]. This together with the equality
![]() $\alpha -s_1=\beta \simeq \alpha ^*-s_1$
implies equation (2.38), which in its turn implies that
$\alpha -s_1=\beta \simeq \alpha ^*-s_1$
implies equation (2.38), which in its turn implies that
![]() ${\partial \psi ^*}(\alpha ,0)/{\partial \psi }>0$
. Together with equation (2.37), this implies non-degeneracy of the Jacobian matrix of the vector function
${\partial \psi ^*}(\alpha ,0)/{\partial \psi }>0$
. Together with equation (2.37), this implies non-degeneracy of the Jacobian matrix of the vector function
![]() $(\alpha ^*(\alpha ,\psi ),\psi ^*(\alpha ,\psi ))$
at the line
$(\alpha ^*(\alpha ,\psi ),\psi ^*(\alpha ,\psi ))$
at the line
![]() $\{\psi =0\}$
. This proves Proposition 2.19.
$\{\psi =0\}$
. This proves Proposition 2.19.
The function
![]() $\widehat G(\alpha ,\psi )=\widetilde {G}(s_1,\phi _1)$
is smooth in
$\widehat G(\alpha ,\psi )=\widetilde {G}(s_1,\phi _1)$
is smooth in
![]() $(\alpha ,\psi )$
, as was shown above. Hence, it is smooth on
$(\alpha ,\psi )$
, as was shown above. Hence, it is smooth on
![]() $W\cup \widehat {\gamma }$
(Proposition 2.19). It has non-zero differential on W, by Proposition 2.16. It remains to show that it has non-zero differential at each point
$W\cup \widehat {\gamma }$
(Proposition 2.19). It has non-zero differential on W, by Proposition 2.16. It remains to show that it has non-zero differential at each point
![]() $x\in \widehat {\gamma }$
. Indeed, it is smooth in the coordinates
$x\in \widehat {\gamma }$
. Indeed, it is smooth in the coordinates
![]() $(s_1,y_1)$
(in which
$(s_1,y_1)$
(in which
![]() $y_1|_{\widehat {\gamma }}\equiv 0 $
), and one has
$y_1|_{\widehat {\gamma }}\equiv 0 $
), and one has
by Proposition 2.16. However, as
![]() $s_1,s_2\to s$
, one has
$s_1,s_2\to s$
, one has
![]() $y_1,\phi _1\to 0$
and
$y_1,\phi _1\to 0$
and
 $$ \begin{align*} y_1=1-\cos\phi_1=\tfrac12\phi_1^2(1+o(1)),\quad \psi=\bigg(\frac{s_2-s_1}2\bigg)^2, \quad s_2-s_1\simeq2(\kappa(s))^{-1}\phi_1. \end{align*} $$
$$ \begin{align*} y_1=1-\cos\phi_1=\tfrac12\phi_1^2(1+o(1)),\quad \psi=\bigg(\frac{s_2-s_1}2\bigg)^2, \quad s_2-s_1\simeq2(\kappa(s))^{-1}\phi_1. \end{align*} $$
Hence,
![]() $y_1\simeq \tfrac 12\kappa ^2(s)\psi $
. This together with equation (2.39) implies that in the coordinates
$y_1\simeq \tfrac 12\kappa ^2(s)\psi $
. This together with equation (2.39) implies that in the coordinates
![]() $(\alpha ,\psi )$
, one has
$(\alpha ,\psi )$
, one has
![]() ${\partial \widehat G}(\alpha ,0)/{\partial \psi }>0$
. Together with the above discussion, this proves Lemma 2.17.
${\partial \widehat G}(\alpha ,0)/{\partial \psi }>0$
. Together with the above discussion, this proves Lemma 2.17.
Proof of existence in Theorem 1.9
The function G defined on the set
![]() $W\cup \widehat {\gamma }$
in the space of lines is invariant under the billiard ball map. Therefore, its level curves are invariant families of lines. They form a
$W\cup \widehat {\gamma }$
in the space of lines is invariant under the billiard ball map. Therefore, its level curves are invariant families of lines. They form a
![]() $C^{\infty }$
-smooth foliation of
$C^{\infty }$
-smooth foliation of
![]() $W\cup \widehat {\gamma }$
, with
$W\cup \widehat {\gamma }$
, with
![]() $\widehat {\gamma }$
being a leaf. Let us denote the latter foliation by
$\widehat {\gamma }$
being a leaf. Let us denote the latter foliation by
![]() ${\mathcal F}$
. The enveloping curves of the curve
${\mathcal F}$
. The enveloping curves of the curve
![]() $\widehat {\gamma }$
and of its leaves are respectively the curve
$\widehat {\gamma }$
and of its leaves are respectively the curve
![]() $\gamma $
and caustics of the billiard on
$\gamma $
and caustics of the billiard on
![]() $\gamma $
. Let us show that they lie on its convex side and there exists a domain
$\gamma $
. Let us show that they lie on its convex side and there exists a domain
![]() $U\subset {\mathbb R}^2$
adjacent to
$U\subset {\mathbb R}^2$
adjacent to
![]() $\gamma $
from the convex side such that the latter caustics form a
$\gamma $
from the convex side such that the latter caustics form a
![]() $C^{\infty }$
-smooth foliation of
$C^{\infty }$
-smooth foliation of
![]() $U\cup \gamma $
, with
$U\cup \gamma $
, with
![]() $\gamma $
being a leaf.
$\gamma $
being a leaf.
Fix a projective duality sending lines to points, e.g., polar duality with respect to the unit circle centered at a point O in the convex domain bounded by
![]() $\gamma $
. Let us shrink W so that its points represent lines that do not pass through O. Then the duality represents the subset
$\gamma $
. Let us shrink W so that its points represent lines that do not pass through O. Then the duality represents the subset
![]() $W\cup \widehat {\gamma }$
in the space of lines as a domain in the affine chart
$W\cup \widehat {\gamma }$
in the space of lines as a domain in the affine chart
![]() ${\mathbb R}^2\subset {\mathbb {RP}}^2$
with a boundary curve. The latter domain and curve will be also denoted by W and
${\mathbb R}^2\subset {\mathbb {RP}}^2$
with a boundary curve. The latter domain and curve will be also denoted by W and
![]() $\widehat {\gamma }$
respectively. The curve
$\widehat {\gamma }$
respectively. The curve
![]() $\widehat {\gamma }$
is dual to
$\widehat {\gamma }$
is dual to
![]() $\gamma $
.
$\gamma $
.
Proposition 2.21. The curve
![]() $\widehat {\gamma }$
is strictly convex, and the domain W lies on its concave side.
$\widehat {\gamma }$
is strictly convex, and the domain W lies on its concave side.
Proof. The curve
![]() $\widehat {\gamma }$
is strictly convex, being dual to the strictly convex curve
$\widehat {\gamma }$
is strictly convex, being dual to the strictly convex curve
![]() $\gamma $
. Each point
$\gamma $
. Each point
![]() $x\in W$
is dual to a line intersecting
$x\in W$
is dual to a line intersecting
![]() $\gamma $
twice. Therefore, there are two tangent lines to
$\gamma $
twice. Therefore, there are two tangent lines to
![]() $\widehat {\gamma }$
through x. Hence, x lies on the concave side from
$\widehat {\gamma }$
through x. Hence, x lies on the concave side from
![]() $\widehat {\gamma }$
.
$\widehat {\gamma }$
.
For every
![]() $x\in W$
, let
$x\in W$
, let
![]() ${\mathcal F}_x\subset {\mathbb R}^2\subset {\mathbb {RP}}^2$
denote the leaf through x of the foliation
${\mathcal F}_x\subset {\mathbb R}^2\subset {\mathbb {RP}}^2$
denote the leaf through x of the foliation
![]() ${\mathcal F}$
(represented in the above dual chart), and let
${\mathcal F}$
(represented in the above dual chart), and let
![]() $L_x$
denote its projective tangent line at x. The enveloping curve of the family of lines represented by the curve
$L_x$
denote its projective tangent line at x. The enveloping curve of the family of lines represented by the curve
![]() ${\mathcal F}_x$
(treated now as a subset in the space of lines) is its dual curve
${\mathcal F}_x$
(treated now as a subset in the space of lines) is its dual curve
![]() ${\mathcal F}_x^*$
. It consists of points
${\mathcal F}_x^*$
. It consists of points
![]() $L_y^*$
dual to the lines
$L_y^*$
dual to the lines
![]() $L_y$
for all
$L_y$
for all
![]() $y\in {\mathcal F}_x$
. Recall that the boundary curve
$y\in {\mathcal F}_x$
. Recall that the boundary curve
![]() $\widehat {\gamma }$
is a strictly convex leaf.
$\widehat {\gamma }$
is a strictly convex leaf.
Proposition 2.22. Shrinking the domain W adjacent to
![]() $\widehat {\gamma }$
one can achieve that the map
$\widehat {\gamma }$
one can achieve that the map
![]() $x\mapsto L_x^*$
be a
$x\mapsto L_x^*$
be a
![]() $C^{\infty }$
-smooth diffeomorphism of the domain
$C^{\infty }$
-smooth diffeomorphism of the domain
![]() $W\cup \widehat {\gamma }$
onto a domain
$W\cup \widehat {\gamma }$
onto a domain
![]() $U\subset {\mathbb R}^2\subset {\mathbb {RP}}^2$
taken together with its boundary arc
$U\subset {\mathbb R}^2\subset {\mathbb {RP}}^2$
taken together with its boundary arc
![]() $\gamma $
. The domain U lies on the convex side from the curve
$\gamma $
. The domain U lies on the convex side from the curve
![]() $\gamma $
.
$\gamma $
.
Proof. The curve
![]() $\widehat {\gamma }$
is strictly convex. No tangent line passes through O, being dual to a point of the curve
$\widehat {\gamma }$
is strictly convex. No tangent line passes through O, being dual to a point of the curve
![]() $\gamma $
(which is a finite point), since the dual to O is the infinity line. Therefore, every compact arc in
$\gamma $
(which is a finite point), since the dual to O is the infinity line. Therefore, every compact arc in
![]() $\widehat {\gamma }$
has a neighborhood in
$\widehat {\gamma }$
has a neighborhood in
![]() ${\mathbb R}^2$
whose intersection with each leaf of the foliation
${\mathbb R}^2$
whose intersection with each leaf of the foliation
![]() ${\mathcal F}$
is a strictly convex curve. Each tangent line to
${\mathcal F}$
is a strictly convex curve. Each tangent line to
![]() $\widehat {\gamma }$
intersects
$\widehat {\gamma }$
intersects
![]() $\widehat {\gamma }$
only at one point: their unique tangency point. This follows from the fact that through each point
$\widehat {\gamma }$
only at one point: their unique tangency point. This follows from the fact that through each point
![]() $A\in \gamma $
passes a unique line tangent to
$A\in \gamma $
passes a unique line tangent to
![]() $\gamma $
, namely its tangent line at A, since
$\gamma $
, namely its tangent line at A, since
![]() $\gamma $
bounds a strictly convex domain. Thus, shrinking W, we can and will consider that each leaf
$\gamma $
bounds a strictly convex domain. Thus, shrinking W, we can and will consider that each leaf
![]() ${\mathcal L}$
is strictly convex, no tangent line passes through O, and each tangent line intersects
${\mathcal L}$
is strictly convex, no tangent line passes through O, and each tangent line intersects
![]() ${\mathcal L}$
at one point: their unique tangency point. Hence, each line L tangent to
${\mathcal L}$
at one point: their unique tangency point. Hence, each line L tangent to
![]() ${\mathcal L}$
is disjoint from the leaves lying on the convex side from
${\mathcal L}$
is disjoint from the leaves lying on the convex side from
![]() ${\mathcal L}$
. Thus, L is disjoint from
${\mathcal L}$
. Thus, L is disjoint from
![]() $\widehat {\gamma }$
and
$\widehat {\gamma }$
and
![]() $O\notin L$
. Let U denote the set of points dual to lines tangent to leaves in W. In the dual picture, the latter statements mean that
$O\notin L$
. Let U denote the set of points dual to lines tangent to leaves in W. In the dual picture, the latter statements mean that
![]() $U\subset {\mathbb R}^2$
and for every
$U\subset {\mathbb R}^2$
and for every
![]() $A=L^*\in U$
, there are no tangent lines to
$A=L^*\in U$
, there are no tangent lines to
![]() $\gamma $
passing through A. The set U is path-connected, disjoint from
$\gamma $
passing through A. The set U is path-connected, disjoint from
![]() $\gamma $
, and it accumulates to all of
$\gamma $
, and it accumulates to all of
![]() $\gamma $
. Therefore, it approaches
$\gamma $
. Therefore, it approaches
![]() $\gamma $
from the convex side, by the previous statement. Hence, it lies entirely on its convex side. Let us now prove that shrinking W, one can achieve that the map
$\gamma $
from the convex side, by the previous statement. Hence, it lies entirely on its convex side. Let us now prove that shrinking W, one can achieve that the map
![]() $x\mapsto L_x^*$
be a diffeomorphism
$x\mapsto L_x^*$
be a diffeomorphism
![]() $W\cup \widehat {\gamma }\to U\cup \gamma $
.
$W\cup \widehat {\gamma }\to U\cup \gamma $
.
Fix a compact arc exhaustion
For every k, fix a flowbox
![]() $\Pi _k\subset W$
of the foliation
$\Pi _k\subset W$
of the foliation
![]() ${\mathcal F}$
adjacent to
${\mathcal F}$
adjacent to
![]() $\widehat {\gamma }_k$
whose leaves are strictly convex. We construct the flowboxes
$\widehat {\gamma }_k$
whose leaves are strictly convex. We construct the flowboxes
![]() $\Pi _k$
with decreasing heights, which means that for every k, each leaf of the flowbox
$\Pi _k$
with decreasing heights, which means that for every k, each leaf of the flowbox
![]() $\Pi _{k+1}$
crosses
$\Pi _{k+1}$
crosses
![]() $\Pi _k$
. Now replace W by the union
$\Pi _k$
. Now replace W by the union
![]() $\bigcup _k\Pi _k$
, which will be now denoted by W. The leaves of the foliation on
$\bigcup _k\Pi _k$
, which will be now denoted by W. The leaves of the foliation on
![]() $W\cup \widehat {\gamma }$
are strictly convex and connected, by construction. We claim that the map
$W\cup \widehat {\gamma }$
are strictly convex and connected, by construction. We claim that the map
![]() $x\mapsto L_x$
, and hence
$x\mapsto L_x$
, and hence
![]() $x\mapsto L_x^*$
, is a
$x\mapsto L_x^*$
, is a
![]() $C^\infty $
-smooth diffeomorphism. Indeed, it is a local diffeomorphism by strict convexity of leaves. It remains to show that
$C^\infty $
-smooth diffeomorphism. Indeed, it is a local diffeomorphism by strict convexity of leaves. It remains to show that
![]() $L_x\neq L_y$
for every distinct
$L_x\neq L_y$
for every distinct
![]() $x,y\in W$
. Indeed, fix an
$x,y\in W$
. Indeed, fix an
![]() $x\in W$
, let
$x\in W$
, let
![]() ${\mathcal L}$
denote the leaf of the foliation
${\mathcal L}$
denote the leaf of the foliation
![]() ${\mathcal F}$
through x. Set
${\mathcal F}$
through x. Set
![]() $L=L_x$
. Fix a k such that
$L=L_x$
. Fix a k such that
![]() $x\in \Pi _k$
. Every leaf in the flowbox
$x\in \Pi _k$
. Every leaf in the flowbox
![]() $\Pi _k$
that does not lie in its leaf through x either intersects L transversally or is disjoint from L, by convexity. Then the latter statement also holds for every other flowbox
$\Pi _k$
that does not lie in its leaf through x either intersects L transversally or is disjoint from L, by convexity. Then the latter statement also holds for every other flowbox
![]() $\Pi _\ell $
, by construction and convexity. This implies that L can be tangent to no other leaf in W. It cannot be tangent to the same leaf
$\Pi _\ell $
, by construction and convexity. This implies that L can be tangent to no other leaf in W. It cannot be tangent to the same leaf
![]() ${\mathcal L}$
at another point
${\mathcal L}$
at another point
![]() $y\neq x$
: leaves have no bitangent lines, by construction. This proves diffeomorphicity of the map
$y\neq x$
: leaves have no bitangent lines, by construction. This proves diffeomorphicity of the map
![]() $x\mapsto L_x^*$
.
$x\mapsto L_x^*$
.
The above
![]() $C^{\infty }$
-smooth diffeomorphism
$C^{\infty }$
-smooth diffeomorphism
![]() $x\mapsto L_x^*$
sends W onto a domain
$x\mapsto L_x^*$
sends W onto a domain
![]() $U\subset {\mathbb R}^2$
adjacent to
$U\subset {\mathbb R}^2$
adjacent to
![]() $\gamma $
. It sends leaves of the foliation
$\gamma $
. It sends leaves of the foliation
![]() ${\mathcal F}$
to the corresponding caustics of the billiard on
${\mathcal F}$
to the corresponding caustics of the billiard on
![]() $\gamma $
. Hence, the caustics together with the curve
$\gamma $
. Hence, the caustics together with the curve
![]() $\gamma $
form a
$\gamma $
form a
![]() $C^{\infty }$
-smooth foliation of
$C^{\infty }$
-smooth foliation of
![]() $U\cup \gamma $
. Constructing the above flowboxes
$U\cup \gamma $
. Constructing the above flowboxes
![]() $\Pi _k$
narrow enough in the transversal direction (step by step), we can achieve that for every
$\Pi _k$
narrow enough in the transversal direction (step by step), we can achieve that for every
![]() $x\in \gamma $
and every leaf
$x\in \gamma $
and every leaf
![]() ${\mathcal L}$
of the foliation
${\mathcal L}$
of the foliation
![]() ${\mathcal F}$
, there are at most two tangent lines through x to the caustic
${\mathcal F}$
, there are at most two tangent lines through x to the caustic
![]() ${\mathcal L}^*$
. Indeed, each leaf
${\mathcal L}^*$
. Indeed, each leaf
![]() ${\mathcal L}$
of the foliation
${\mathcal L}$
of the foliation
![]() ${\mathcal F}$
is a leaf of some flowbox
${\mathcal F}$
is a leaf of some flowbox
![]() $\Pi _k$
. Its dual caustic
$\Pi _k$
. Its dual caustic
![]() ${\mathcal L}^*$
is convex, as is
${\mathcal L}^*$
is convex, as is
![]() ${\mathcal L}$
. It will satisfy the above tangent line statement if the total angle increment of its tangent vector is no greater than
${\mathcal L}$
. It will satisfy the above tangent line statement if the total angle increment of its tangent vector is no greater than
![]() $\pi $
. The latter angle increment statement holds for the curve
$\pi $
. The latter angle increment statement holds for the curve
![]() $\gamma $
. Hence, it remains valid for the caustics dual to the leaves of the flowbox
$\gamma $
. Hence, it remains valid for the caustics dual to the leaves of the flowbox
![]() $\Pi _k$
if
$\Pi _k$
if
![]() $\Pi _k$
is chosen narrow enough. The existence statement (1) of Theorem 1.9 is proved.
$\Pi _k$
is chosen narrow enough. The existence statement (1) of Theorem 1.9 is proved.
The existence statement (2) of Theorem 1.9 (the case when
![]() $\gamma $
is an arc) is proved analogously with small modifications. We deal with the billiard map
$\gamma $
is an arc) is proved analogously with small modifications. We deal with the billiard map
![]() $\widetilde {\delta }_+=I\circ \beta $
acting on the restriction to
$\widetilde {\delta }_+=I\circ \beta $
acting on the restriction to
![]() $\gamma $
of the unit tangent bundle to
$\gamma $
of the unit tangent bundle to
![]() ${\mathbb R}^2$
. The map
${\mathbb R}^2$
. The map
![]() $I:(q',u)\mapsto (q',u^*)$
is the symmetry of a vector
$I:(q',u)\mapsto (q',u^*)$
is the symmetry of a vector
![]() $u\in T_{q'}{\mathbb R}^2$
,
$u\in T_{q'}{\mathbb R}^2$
,
![]() $q'\in \gamma $
, with respect to the tangent line
$q'\in \gamma $
, with respect to the tangent line
![]() $T_{q'}\gamma $
. The map
$T_{q'}\gamma $
. The map
![]() $\beta (q,u)=(q',u')$
is defined for u close enough to
$\beta (q,u)=(q',u')$
is defined for u close enough to
![]() $\dot \gamma (q)$
, with q,
$\dot \gamma (q)$
, with q,
![]() $q'$
being the same, as in §1.3, Case (2), Remark 1.21; the unit vectors
$q'$
being the same, as in §1.3, Case (2), Remark 1.21; the unit vectors
![]() $u\in T_q{\mathbb R}^2$
,
$u\in T_q{\mathbb R}^2$
,
![]() $u'\in T_{q'}{\mathbb R}^2$
being tangent to the line
$u'\in T_{q'}{\mathbb R}^2$
being tangent to the line
![]() $qq'$
and inducing the same orientation of this line. The corresponding map
$qq'$
and inducing the same orientation of this line. The corresponding map
![]() $F=\delta _+:(s_1,y_1)\mapsto (s_2,y_2)$
from equation (1.3) with
$F=\delta _+:(s_1,y_1)\mapsto (s_2,y_2)$
from equation (1.3) with
![]() $s_1=s(q)<s_2=s(q')$
is a well-defined
$s_1=s(q)<s_2=s(q')$
is a well-defined
![]() $C^\infty $
-lifted strongly billiard-like map on the union of the natural parameter interval
$C^\infty $
-lifted strongly billiard-like map on the union of the natural parameter interval
![]() $J=(a,b)=(a,b)\times \{0\}$
of the curve
$J=(a,b)=(a,b)\times \{0\}$
of the curve
![]() $\gamma $
and a domain in
$\gamma $
and a domain in
![]() ${\mathbb R}\times {\mathbb R}_+$
adjacent to it. Now the map
${\mathbb R}\times {\mathbb R}_+$
adjacent to it. Now the map
![]() $\Lambda $
sending
$\Lambda $
sending
![]() $(s_1,y_1)$
to the corresponding oriented line is a local
$(s_1,y_1)$
to the corresponding oriented line is a local
![]() $C^\infty $
-smooth diffeomorphism. The modified Lemma 2.17 adapted to the case under consideration states that the F-invariant function G is locally
$C^\infty $
-smooth diffeomorphism. The modified Lemma 2.17 adapted to the case under consideration states that the F-invariant function G is locally
![]() $C^\infty $
-smooth (up to the boundary) with non-zero differential as a function of a line. The above proof of Lemma 2.17 remains valid, since it uses only local arguments. The modified Lemma 2.17 implies (analogously to the above discussion) that the foliation
$C^\infty $
-smooth (up to the boundary) with non-zero differential as a function of a line. The above proof of Lemma 2.17 remains valid, since it uses only local arguments. The modified Lemma 2.17 implies (analogously to the above discussion) that the foliation
![]() $G=\mathrm {const.}$
with leaves represented as smooth families of lines induces a
$G=\mathrm {const.}$
with leaves represented as smooth families of lines induces a
![]() $C^\infty $
-smooth foliation by caustics (their enveloping curves) on an appropriate domain adjacent to
$C^\infty $
-smooth foliation by caustics (their enveloping curves) on an appropriate domain adjacent to
![]() $\gamma $
from its convex side; smooth up to the boundary. If
$\gamma $
from its convex side; smooth up to the boundary. If
![]() $\gamma $
is an arc, then we need not prove that for every
$\gamma $
is an arc, then we need not prove that for every
![]() $x\in \gamma $
and every leaf
$x\in \gamma $
and every leaf
![]() ${\mathcal L}^*$
of the foliation by caustics, there are at most two lines through x tangent to
${\mathcal L}^*$
of the foliation by caustics, there are at most two lines through x tangent to
![]() ${\mathcal L}^*$
. Indeed, the latter tangent line condition (which is required in the definition of foliation by caustics for
${\mathcal L}^*$
. Indeed, the latter tangent line condition (which is required in the definition of foliation by caustics for
![]() $\gamma $
being an unbounded submanifold) is not required for
$\gamma $
being an unbounded submanifold) is not required for
![]() $\gamma $
being an arc: see Remark 1.7.
$\gamma $
being an arc: see Remark 1.7.
The proof of the existence in Theorem 1.12 repeats the above proof of the existence in Theorem 1.9 with obvious changes. The existence statement of Theorem 1.13 follows from that of Theorem 1.12.
2.8 Space of foliations. Proofs of Theorems 1.31, 1.34, and 1.35 and Proposition 1.33
Proof of Theorem 1.31
It suffices to prove the statement of Theorem 1.31 for foliations from Theorems 1.26 and 1.30, since the foliations in Theorems 1.9, 1.12, and 1.13 are obtained from foliations in Theorem 1.26 by duality, see the above subsection.
Case of Theorem 1.26. Consider a
![]() $C^{\infty }$
-lifted strongly billiard-like map. We already know that in appropriate coordinates, it takes the form in equation (1.12):
$C^{\infty }$
-lifted strongly billiard-like map. We already know that in appropriate coordinates, it takes the form in equation (1.12):
The function h is F-invariant, and so are its level lines.
Suppose the contrary: there exists another
![]() $C^{\infty }$
-smooth F-invariant function
$C^{\infty }$
-smooth F-invariant function
![]() $G(\tau ,h)$
,
$G(\tau ,h)$
,
![]() $G(\tau ,0)\equiv 0$
, without critical points on
$G(\tau ,0)\equiv 0$
, without critical points on
![]() $J=\{ h=0\}$
and such that there exists an
$J=\{ h=0\}$
and such that there exists an
![]() $x\in J$
where the foliations
$x\in J$
where the foliations
![]() $G=\mathrm {const.}$
and
$G=\mathrm {const.}$
and
![]() $h=\mathrm {const.}$
have different k-jets for some k. Without loss of generality, we consider that
$h=\mathrm {const.}$
have different k-jets for some k. Without loss of generality, we consider that
![]() $x=(0,0)$
, shifting the coordinate
$x=(0,0)$
, shifting the coordinate
![]() $\tau $
. Then the asymptotic Taylor series of the function G at x contains at least one monomial
$\tau $
. Then the asymptotic Taylor series of the function G at x contains at least one monomial
![]() $a_{mn}\tau ^mh^n$
with
$a_{mn}\tau ^mh^n$
with
![]() $m\geq 1$
and a non-zero coefficient
$m\geq 1$
and a non-zero coefficient
![]() $a_{mn}$
. Set
$a_{mn}$
. Set
Consider the lower
![]() $(1,2)$
-quasihomogeneous terms containing
$(1,2)$
-quasihomogeneous terms containing
![]() $\tau$
:
$\tau$
:
 $$ \begin{align*} G_d(\tau,h):=\sum_{(m,n)\in{\mathcal N},\ m+2n=d}a_{mn}\tau^mh^n. \end{align*} $$
$$ \begin{align*} G_d(\tau,h):=\sum_{(m,n)\in{\mathcal N},\ m+2n=d}a_{mn}\tau^mh^n. \end{align*} $$
One has
![]() $G\circ F(\tau ,h)-G(\tau ,h)\equiv 0$
. However,
$G\circ F(\tau ,h)-G(\tau ,h)\equiv 0$
. However,
 $$ \begin{align} G\circ F(\tau,h) -G(\tau,h)&=G(\tau+\sqrt h,h)-G(\tau,h) \notag \\ &=G_d(\tau+\sqrt h,h)-G_d(\tau,h)+\text{ higher terms}. \end{align} $$
$$ \begin{align} G\circ F(\tau,h) -G(\tau,h)&=G(\tau+\sqrt h,h)-G(\tau,h) \notag \\ &=G_d(\tau+\sqrt h,h)-G_d(\tau,h)+\text{ higher terms}. \end{align} $$
Here ‘higher terms’ means ‘a function that admits an asymptotic Taylor series in
![]() $(\tau ,\sqrt h)$
at
$(\tau ,\sqrt h)$
at
![]() $(0,0)$
that contains only terms
$(0,0)$
that contains only terms
![]() $a_{mn}\tau ^\alpha h^\beta $
of quasihomogeneous degrees
$a_{mn}\tau ^\alpha h^\beta $
of quasihomogeneous degrees
![]() $\alpha +2\beta>d$
’. Let
$\alpha +2\beta>d$
’. Let
![]() $m_0$
denote the higher degree of
$m_0$
denote the higher degree of
![]() $\tau $
in a monomial entering
$\tau $
in a monomial entering
![]() $G_d$
. The difference
$G_d$
. The difference
![]() $G_d(\tau +\sqrt h,h)-G_d(\tau ,h)$
is quasihomogeneous of degree d. It contains the monomial
$G_d(\tau +\sqrt h,h)-G_d(\tau ,h)$
is quasihomogeneous of degree d. It contains the monomial
![]() $\tau ^{m_0-1}h^\ell $
,
$\tau ^{m_0-1}h^\ell $
,
![]() $m_0-1+2\ell =d$
,
$m_0-1+2\ell =d$
,
![]() $\ell \in \tfrac 12+{\mathbb Z}$
, with non-zero coefficient, by construction. This monomial will not cancel out with other monomials in the asymptotic Taylor series of the difference
$\ell \in \tfrac 12+{\mathbb Z}$
, with non-zero coefficient, by construction. This monomial will not cancel out with other monomials in the asymptotic Taylor series of the difference
![]() $G\circ F(\tau ,h)- G(\tau ,h)$
, by construction. Therefore, the latter difference cannot be identically equal to zero. The contradiction thus obtained proves the statement of Theorem 1.31 in the conditions of Theorem 1.26.
$G\circ F(\tau ,h)- G(\tau ,h)$
, by construction. Therefore, the latter difference cannot be identically equal to zero. The contradiction thus obtained proves the statement of Theorem 1.31 in the conditions of Theorem 1.26.
Case of Theorem 1.30. In this case, we know that the map in question is conjugated to
![]() $(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
. The statement of Theorem 1.31 for the latter map is proved by the above arguments for lower homogeneous (that is,
$(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
. The statement of Theorem 1.31 for the latter map is proved by the above arguments for lower homogeneous (that is,
![]() $(1,1)$
-quasihomogeneous) terms of the Taylor series of the function G.
$(1,1)$
-quasihomogeneous) terms of the Taylor series of the function G.
Proof of Proposition 1.33
Let
![]() $g(\tau ,h)$
be a
$g(\tau ,h)$
be a
![]() $C^\infty $
-smooth function invariant under the map
$C^\infty $
-smooth function invariant under the map
![]() $F:(\tau ,h)\mapsto (\tau +\sqrt h,h)$
that has type in equation (1.15):
$F:(\tau ,h)\mapsto (\tau +\sqrt h,h)$
that has type in equation (1.15):
Invariance is equivalent to the equality
![]() $g(\tau +\sqrt h,h)=g(\tau ,h)$
. This together with equation (2.42) implies that
$g(\tau +\sqrt h,h)=g(\tau ,h)$
. This together with equation (2.42) implies that
Moreover, the function
![]() $\psi (s,h)$
is
$\psi (s,h)$
is
![]() $C^{\infty }$
-smooth and h-flat on a cylinder
$C^{\infty }$
-smooth and h-flat on a cylinder
![]() $S^1\times [0,\delta )$
,
$S^1\times [0,\delta )$
,
![]() $S^1={\mathbb R}_{s} / {\mathbb Z}$
, for a small
$S^1={\mathbb R}_{s} / {\mathbb Z}$
, for a small
![]() $\delta>0$
. This follows from smoothness and h-flatness of the function
$\delta>0$
. This follows from smoothness and h-flatness of the function
![]() $g(\tau ,h)-h$
. Conversely, consider an h-flat function
$g(\tau ,h)-h$
. Conversely, consider an h-flat function
![]() $\psi (s,h)$
that is 1-periodic in s and such that
$\psi (s,h)$
that is 1-periodic in s and such that
![]() $\psi (0,h)=0$
. Then the function
$\psi (0,h)=0$
. Then the function
 $$ \begin{align*} g(\tau,h):=\psi\bigg(\frac\tau{\sqrt h},h\bigg)+h \end{align*} $$
$$ \begin{align*} g(\tau,h):=\psi\bigg(\frac\tau{\sqrt h},h\bigg)+h \end{align*} $$
is
![]() $C^{\infty }$
-smooth, F-invariant, and its difference with h is h-flat, by construction. Statement (1) of Proposition 1.33 is proved. Statement (2) can be reduced to statement (1) and also can be proved analogously.
$C^{\infty }$
-smooth, F-invariant, and its difference with h is h-flat, by construction. Statement (1) of Proposition 1.33 is proved. Statement (2) can be reduced to statement (1) and also can be proved analogously.
Theorem 1.34 follows immediately from Proposition 1.33, and in its turn, it immediately implies Theorem 1.35.
2.9 Proof of Proposition 1.36 and non-uniqueness in main theorems
Proof of Proposition 1.36
Let us prove the statement of Proposition 1.36 for a map
![]() $\widetilde {F}$
of the type in equation (1.13). We prove it for line fields: for other objects, the proof is analogous. Without loss of generality, we can and will consider that the map
$\widetilde {F}$
of the type in equation (1.13). We prove it for line fields: for other objects, the proof is analogous. Without loss of generality, we can and will consider that the map
![]() $\widetilde {F}$
takes the form
$\widetilde {F}$
takes the form
![]() $(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
: see statement (2) of Theorem 1.30. Let
$(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
: see statement (2) of Theorem 1.30. Let
![]() $G_1$
and
$G_1$
and
![]() $G_2$
be two
$G_2$
be two
![]() $\widetilde {F}$
-invariant line fields on W with distinct germs at J. This means that there exists a sequence of points
$\widetilde {F}$
-invariant line fields on W with distinct germs at J. This means that there exists a sequence of points
![]() $x(k)=(\tau (k),\phi (k))$
with
$x(k)=(\tau (k),\phi (k))$
with
![]() $\phi (k)\to 0$
and
$\phi (k)\to 0$
and
![]() $\tau (k)$
lying in a compact subset in J such that the lines
$\tau (k)$
lying in a compact subset in J such that the lines
![]() $G_1(x(k)),G_2(x(k))\subset T_{x(k)}{\mathbb R}^2$
are distinct. Taking a subsequence, we can and will consider that
$G_1(x(k)),G_2(x(k))\subset T_{x(k)}{\mathbb R}^2$
are distinct. Taking a subsequence, we can and will consider that
![]() $x(k)\to x=(\tau _0,0)$
, as
$x(k)\to x=(\tau _0,0)$
, as
![]() $k\to \infty $
. The two-sided orbit of a point
$k\to \infty $
. The two-sided orbit of a point
![]() $x(k)$
with big k consists of points with
$x(k)$
with big k consists of points with
![]() $\phi $
-coordinate
$\phi $
-coordinate
![]() $\phi (k)$
whose
$\phi (k)$
whose
![]() $\tau $
-coordinates form an arithmetic progression with step
$\tau $
-coordinates form an arithmetic progression with step
![]() $\phi (k)$
converging to zero. At each point of the orbit, the lines of the fields
$\phi (k)$
converging to zero. At each point of the orbit, the lines of the fields
![]() $G_1$
and
$G_1$
and
![]() $G_2$
are distinct, since this holds at
$G_2$
are distinct, since this holds at
![]() $x(k)$
and by
$x(k)$
and by
![]() $\widetilde {F}$
-invariance. Therefore, passing to limit, as
$\widetilde {F}$
-invariance. Therefore, passing to limit, as
![]() $k\to \infty $
, we get that for every point
$k\to \infty $
, we get that for every point
![]() $z\in J$
, there exist points
$z\in J$
, there exist points
![]() $z'$
arbitrarily close to z with
$z'$
arbitrarily close to z with
![]() $G_1(z')\neq G_2(z')$
. Hence, the germs at z of the line fields
$G_1(z')\neq G_2(z')$
. Hence, the germs at z of the line fields
![]() $G_1$
and
$G_1$
and
![]() $G_2$
are distinct. The first statement of Proposition 1.36, for a map
$G_2$
are distinct. The first statement of Proposition 1.36, for a map
![]() $\widetilde {F}$
of the type in equation (1.13), is proved. Its second statement, for a
$\widetilde {F}$
of the type in equation (1.13), is proved. Its second statement, for a
![]() $C^\infty $
-lifted strongly billiard-like map
$C^\infty $
-lifted strongly billiard-like map
![]() $F:V\cup J\to F(V\cup J)\subset {\mathbb R}^2$
, follows from its first statement and the fact that F is conjugated to the map
$F:V\cup J\to F(V\cup J)\subset {\mathbb R}^2$
, follows from its first statement and the fact that F is conjugated to the map
![]() $(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
by a homeomorphism that is smooth on the complement to the boundary interval J. The latter conjugating homeomorphism is the composition of a diffeomorphism conjugating F to the map
$(\tau ,\phi )\mapsto (\tau +\phi ,\phi )$
by a homeomorphism that is smooth on the complement to the boundary interval J. The latter conjugating homeomorphism is the composition of a diffeomorphism conjugating F to the map
![]() $(\tau ,h)\mapsto (\tau +\sqrt h,h)$
(Theorem 1.27) and the map
$(\tau ,h)\mapsto (\tau +\sqrt h,h)$
(Theorem 1.27) and the map
![]() $(\tau ,h)\mapsto (\tau ,\phi )$
,
$(\tau ,h)\mapsto (\tau ,\phi )$
,
![]() $\phi =\sqrt h$
. Proposition 1.36 is proved.
$\phi =\sqrt h$
. Proposition 1.36 is proved.
Proof of non-uniqueness in Theorems 1.30, 1.26, 1.9, 1.12, and 1.13
Existence of a continuum of distinct germs of foliations satisfying the statements of any of the above-mentioned theorems follows immediately from Proposition 1.36 and Theorem 1.35, which states that there are as many distinct boundary germs as flat functions on the cylinder
![]() $S^1\times {\mathbb R}_{\geq 0}$
with distinct germs at
$S^1\times {\mathbb R}_{\geq 0}$
with distinct germs at
![]() $S^1\times \{0\}$
. It remains to show that there exists a domain adjacent to the boundary interval (or the curve
$S^1\times \{0\}$
. It remains to show that there exists a domain adjacent to the boundary interval (or the curve
![]() $\gamma $
) which admits an infinite-dimensional family of corresponding foliations with distinct germs.
$\gamma $
) which admits an infinite-dimensional family of corresponding foliations with distinct germs.
Case of Theorem 1.30. Fix coordinates
![]() $(\tau ,\phi )$
in which
$(\tau ,\phi )$
in which
![]() $\widetilde {F}(\tau ,\phi )=(\tau +\phi ,\phi )$
. Recall that the coordinates
$\widetilde {F}(\tau ,\phi )=(\tau +\phi ,\phi )$
. Recall that the coordinates
![]() $(\tau ,\phi )$
are defined on
$(\tau ,\phi )$
are defined on
![]() $W\cup J$
, where
$W\cup J$
, where
![]() $W\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to the interval
$W\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to the interval
![]() $J=(a,b)\times \{0\}$
. Without loss of generality, we consider that
$J=(a,b)\times \{0\}$
. Without loss of generality, we consider that
![]() $a<0<b$
. Fix a
$a<0<b$
. Fix a
![]() $C^\infty $
-smooth h-flat function
$C^\infty $
-smooth h-flat function
![]() $\psi $
on the cylinder
$\psi $
on the cylinder
![]() $S^1\times {\mathbb R}_{\geq 0}$
,
$S^1\times {\mathbb R}_{\geq 0}$
,
![]() $S^1={\mathbb R} / {\mathbb Z}$
, with non-trivial germ at
$S^1={\mathbb R} / {\mathbb Z}$
, with non-trivial germ at
![]() $S^1\times \{0\}$
:
$S^1\times \{0\}$
:
For every
![]() ${\varepsilon }>0$
, the function
${\varepsilon }>0$
, the function
 $$ \begin{align} g_{\varepsilon} (\tau,\phi):=\phi+{\varepsilon} \chi(\tau,\phi), \quad \chi(\tau,\phi):=\psi\bigg(\frac{\tau}\phi,\phi\bigg) \end{align} $$
$$ \begin{align} g_{\varepsilon} (\tau,\phi):=\phi+{\varepsilon} \chi(\tau,\phi), \quad \chi(\tau,\phi):=\psi\bigg(\frac{\tau}\phi,\phi\bigg) \end{align} $$
is
![]() $\widetilde {F}$
-invariant,
$\widetilde {F}$
-invariant,
![]() $C^\infty $
-smooth, and well defined on
$C^\infty $
-smooth, and well defined on
![]() $W\cup J$
,
$W\cup J$
,
![]() $g_{\varepsilon } (\tau ,\phi )=\phi +{\operatorname {flat}}(\phi )$
. Let us show that shrinking the domain W one can achieve that the foliation
$g_{\varepsilon } (\tau ,\phi )=\phi +{\operatorname {flat}}(\phi )$
. Let us show that shrinking the domain W one can achieve that the foliation
![]() $g_{\varepsilon } =\mathrm {const.}$
is regular, that is,
$g_{\varepsilon } =\mathrm {const.}$
is regular, that is,
![]() $g_{\varepsilon } $
has no critical points on W, whenever
$g_{\varepsilon } $
has no critical points on W, whenever
![]() ${\varepsilon } $
is small enough.
${\varepsilon } $
is small enough.
Claim 5. Replacing W by a smaller domain adjacent to J, one can achieve that each partial derivative of the function
![]() $\chi $
(of any order) be bounded on W. For any given m and every
$\chi $
(of any order) be bounded on W. For any given m and every
![]() $\delta>0$
shrinking W (depending on m and
$\delta>0$
shrinking W (depending on m and
![]() $\delta $
), one can achieve that all its order m partial derivatives have moduli less than
$\delta $
), one can achieve that all its order m partial derivatives have moduli less than
![]() $\delta $
.
$\delta $
.
Proof. The modulus of each partial derivative of order m admits an upper bound by a quantity
 $$ \begin{align} \bigg\lvert \frac{\partial^m\chi(\tau,\phi)}{\partial \tau^\nu\partial\phi^{m-\nu}}\bigg\rvert \leq c_m(1+ \lvert \tau\rvert^m)(1+\phi^{-2(m+1)})\sum_{\ell,r=1}^m \lvert \psi_{\ell r}\rvert , \end{align} $$
$$ \begin{align} \bigg\lvert \frac{\partial^m\chi(\tau,\phi)}{\partial \tau^\nu\partial\phi^{m-\nu}}\bigg\rvert \leq c_m(1+ \lvert \tau\rvert^m)(1+\phi^{-2(m+1)})\sum_{\ell,r=1}^m \lvert \psi_{\ell r}\rvert , \end{align} $$
 $$ \begin{align*} c_m =\mathrm{const.}>0,\quad \psi_{\ell r}(\tau,\phi)=\frac{\partial^{\ell+r}\psi}{\partial s^\ell\partial\phi^r}\bigg(\frac{\tau}\phi,\phi\bigg)= o(\phi^k) \quad \text{for every } k\in{\mathbb N}. \end{align*} $$
$$ \begin{align*} c_m =\mathrm{const.}>0,\quad \psi_{\ell r}(\tau,\phi)=\frac{\partial^{\ell+r}\psi}{\partial s^\ell\partial\phi^r}\bigg(\frac{\tau}\phi,\phi\bigg)= o(\phi^k) \quad \text{for every } k\in{\mathbb N}. \end{align*} $$
Here the latter
![]() $o(\phi ^k)$
is uniform in
$o(\phi ^k)$
is uniform in
![]() $\tau $
, as
$\tau $
, as
![]() $\phi \to 0$
. Equation (2.46) follows from 1-periodicity and flatness of the function
$\phi \to 0$
. Equation (2.46) follows from 1-periodicity and flatness of the function
![]() $\psi (s,h)$
, and chain rule for calculating derivatives. Let us now replace the domain W by a smaller domain adjacent to J on which the right-hand side in equation (2.46) is bounded for each m and is less than
$\psi (s,h)$
, and chain rule for calculating derivatives. Let us now replace the domain W by a smaller domain adjacent to J on which the right-hand side in equation (2.46) is bounded for each m and is less than
![]() $\delta $
for a given m. To do this, fix an arbitrary
$\delta $
for a given m. To do this, fix an arbitrary
![]() $\eta>0$
. First let us replace W by the connected component adjacent to J of its intersection with the rectangle
$\eta>0$
. First let us replace W by the connected component adjacent to J of its intersection with the rectangle
![]() $(a,b)\times (0,\eta )$
. In the case when
$(a,b)\times (0,\eta )$
. In the case when
![]() $(a,b)$
is a finite interval, the right-hand side in equation (2.46) is uniformly bounded on W and tends to zero uniformly in
$(a,b)$
is a finite interval, the right-hand side in equation (2.46) is uniformly bounded on W and tends to zero uniformly in
![]() $\tau \in (a,b)$
, as
$\tau \in (a,b)$
, as
![]() $\phi \to 0$
. This follows from boundedness of derivatives of the function
$\phi \to 0$
. This follows from boundedness of derivatives of the function
![]() $\psi $
on any compact cylinder
$\psi $
on any compact cylinder
![]() $S^1\times [0,\eta ]$
and from the fact that the asymptotics
$S^1\times [0,\eta ]$
and from the fact that the asymptotics
![]() $\psi _{\ell r}(\tau ,\phi )=o(\phi ^{3m+3})$
kills polynomial growth of the function
$\psi _{\ell r}(\tau ,\phi )=o(\phi ^{3m+3})$
kills polynomial growth of the function
![]() $\phi ^{-2(m+1)}$
. Therefore, shrinking W, one can achieve that for given m and
$\phi ^{-2(m+1)}$
. Therefore, shrinking W, one can achieve that for given m and
![]() $\delta $
, the right-hand side in equation (2.46) be less than
$\delta $
, the right-hand side in equation (2.46) be less than
![]() $\delta $
on W.
$\delta $
on W.
In the case when some (or both) of the boundary points a or b is infinity, take an exhaustion of the interval
![]() $(a,b)$
by segments
$(a,b)$
by segments
![]() $[a_k,b_k]$
. By the above argument, we can take a rectangle
$[a_k,b_k]$
. By the above argument, we can take a rectangle
![]() $\Pi _k=(a_k,b_k)\times (0,d_k)\subset W$
on which for all m, the right-hand sides in equation (2.46) be bounded, and for some given m, the same right-hand side be less than a given
$\Pi _k=(a_k,b_k)\times (0,d_k)\subset W$
on which for all m, the right-hand sides in equation (2.46) be bounded, and for some given m, the same right-hand side be less than a given
![]() $\delta $
. Replacing W by
$\delta $
. Replacing W by
![]() $\bigcup _k\Pi _k$
, we achieve that the two latter inequalities hold on
$\bigcup _k\Pi _k$
, we achieve that the two latter inequalities hold on
![]() $W\cup J$
.
$W\cup J$
.
Let W satisfy the statements of the above claim so that each first partial derivative of the function
![]() $\chi $
has modulus less than
$\chi $
has modulus less than
![]() $\tfrac 12$
. Then for every
$\tfrac 12$
. Then for every
![]() ${\varepsilon } \in [0,1]$
, the foliation
${\varepsilon } \in [0,1]$
, the foliation
![]() ${g_{\varepsilon } =\mathrm {const.}}$
is regular on
${g_{\varepsilon } =\mathrm {const.}}$
is regular on
![]() $W\cup J$
, since for those
$W\cup J$
, since for those
![]() ${\varepsilon } $
, one has
${\varepsilon } $
, one has
![]() ${\partial g_{\varepsilon } }/{\partial \phi }=1+{\varepsilon } ({\partial \chi }/{\partial \phi })>\tfrac 12$
on
${\partial g_{\varepsilon } }/{\partial \phi }=1+{\varepsilon } ({\partial \chi }/{\partial \phi })>\tfrac 12$
on
![]() $W\cup J$
. All its leaves are
$W\cup J$
. All its leaves are
![]() $\widetilde {F}$
-invariant. For distinct values of the parameter
$\widetilde {F}$
-invariant. For distinct values of the parameter
![]() ${\varepsilon } $
the germs of the corresponding foliations are distinct at each point of the interval J, by Theorem 1.35, Proposition 1.36, and non-triviality of the germ at
${\varepsilon } $
the germs of the corresponding foliations are distinct at each point of the interval J, by Theorem 1.35, Proposition 1.36, and non-triviality of the germ at
![]() $S^1\times \{0\}$
of the function
$S^1\times \{0\}$
of the function
![]() $\psi $
. This yields a one-dimensional family of foliations from Theorem 1.30 with pairwise distinct germs at each point in J.
$\psi $
. This yields a one-dimensional family of foliations from Theorem 1.30 with pairwise distinct germs at each point in J.
Now let us apply the above argument with the expression
![]() ${\varepsilon } \chi $
in equation (2.45) being replaced by an arbitrary linear combination
${\varepsilon } \chi $
in equation (2.45) being replaced by an arbitrary linear combination
 $$ \begin{align} \widetilde{\chi}_{\varepsilon} (\tau,\phi)=\sum_{k=1}^N\frac{{\varepsilon} _k}{k!4^k}\psi^k \bigg(\frac{\tau}{\phi},\phi\bigg),\quad {\varepsilon} =({\varepsilon} _1,\ldots,{\varepsilon} _N)\in[0,1]^N. \end{align} $$
$$ \begin{align} \widetilde{\chi}_{\varepsilon} (\tau,\phi)=\sum_{k=1}^N\frac{{\varepsilon} _k}{k!4^k}\psi^k \bigg(\frac{\tau}{\phi},\phi\bigg),\quad {\varepsilon} =({\varepsilon} _1,\ldots,{\varepsilon} _N)\in[0,1]^N. \end{align} $$
Recall that
![]() $\lvert \psi \rvert < \tfrac 18$
. This inequality together with the above assumption that the first partial derivatives of the function
$\lvert \psi \rvert < \tfrac 18$
. This inequality together with the above assumption that the first partial derivatives of the function
![]() $\chi (\tau ,\phi )=\psi ({\tau }/{\phi },\phi )$
have moduli less than
$\chi (\tau ,\phi )=\psi ({\tau }/{\phi },\phi )$
have moduli less than
![]() $\tfrac 12$
on W imply that for every
$\tfrac 12$
on W imply that for every
![]() ${\varepsilon } $
as in equation (2.47), the module of each first partial derivative of the function
${\varepsilon } $
as in equation (2.47), the module of each first partial derivative of the function
![]() $\widetilde {\chi }_{\varepsilon } $
is less than
$\widetilde {\chi }_{\varepsilon } $
is less than
![]() $\tfrac 12$
on
$\tfrac 12$
on
![]() $W\cup J$
. This implies that the foliation by level curves of the function
$W\cup J$
. This implies that the foliation by level curves of the function
![]() $g_{\varepsilon } (\tau ,\phi )=\phi +\widetilde {\chi }_{\varepsilon } $
is a
$g_{\varepsilon } (\tau ,\phi )=\phi +\widetilde {\chi }_{\varepsilon } $
is a
![]() $C^\infty $
-smooth foliation on
$C^\infty $
-smooth foliation on
![]() $W\cup J$
. We get an N-dimensional family of foliations on
$W\cup J$
. We get an N-dimensional family of foliations on
![]() $W\cup J$
depending on
$W\cup J$
depending on
![]() $({\varepsilon } _1,\ldots ,{\varepsilon } _N)\in [0,1]^N$
with pairwise distinct germs at J, and hence, at each point of the curve J (Proposition 1.36). The non-uniqueness statement of Theorem 1.30 is proved.
$({\varepsilon } _1,\ldots ,{\varepsilon } _N)\in [0,1]^N$
with pairwise distinct germs at J, and hence, at each point of the curve J (Proposition 1.36). The non-uniqueness statement of Theorem 1.30 is proved.
Case of Theorem 1.26. Its non-uniqueness statement follows from that of Theorem 1.30 and also from the above arguments.
Case of Theorem 1.9(1). Here,
![]() $\gamma \subset {\mathbb R}^2$
is an unbounded one-dimensional submanifold. Let us consider the billiard ball map acting on lines as a
$\gamma \subset {\mathbb R}^2$
is an unbounded one-dimensional submanifold. Let us consider the billiard ball map acting on lines as a
![]() $C^\infty $
-lifted strongly billiard-like map F. Let us introduce new (symplectic) coordinates
$C^\infty $
-lifted strongly billiard-like map F. Let us introduce new (symplectic) coordinates
![]() $(\tau ,h)$
in which
$(\tau ,h)$
in which
![]() $F(\tau ,h)=(\tau +\sqrt h,h)$
, see equation (1.12). The map F is defined on
$F(\tau ,h)=(\tau +\sqrt h,h)$
, see equation (1.12). The map F is defined on
![]() $W\cup J$
, where
$W\cup J$
, where
![]() $J=(a,b)\times \{0\}$
,
$J=(a,b)\times \{0\}$
,
![]() $a<0<b$
, parameterizes the family of lines tangent to
$a<0<b$
, parameterizes the family of lines tangent to
![]() $\gamma $
and
$\gamma $
and
![]() $W\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J. Representing lines as points in
$W\subset {\mathbb R}\times {\mathbb R}_+$
is a domain adjacent to J. Representing lines as points in
![]() ${\mathbb {RP}}^2$
via a projective duality
${\mathbb {RP}}^2$
via a projective duality
![]() ${\mathbb {RP}}^{2*}\to {\mathbb {RP}}^2$
transforms J to a strictly convex curve
${\mathbb {RP}}^{2*}\to {\mathbb {RP}}^2$
transforms J to a strictly convex curve
![]() $\gamma ^*\subset {\mathbb {RP}}^2$
dual to
$\gamma ^*\subset {\mathbb {RP}}^2$
dual to
![]() $\gamma $
, and W to a domain adjacent to
$\gamma $
, and W to a domain adjacent to
![]() $\gamma ^*$
from the concave side. See §2.7. We can and will consider that
$\gamma ^*$
from the concave side. See §2.7. We can and will consider that
![]() $\gamma ^*$
and W lie in an affine chart
$\gamma ^*$
and W lie in an affine chart
![]() ${\mathbb R}^2$
, as in the proof of the existence in Theorem 1.9 in §2.7. In what follows, we identify J with
${\mathbb R}^2$
, as in the proof of the existence in Theorem 1.9 in §2.7. In what follows, we identify J with
![]() $\gamma ^*$
. Consider the foliation
$\gamma ^*$
. Consider the foliation
![]() $h=\mathrm {const.}$
by F-invariant curves. Let us first construct a one-dimensional family of foliations using a
$h=\mathrm {const.}$
by F-invariant curves. Let us first construct a one-dimensional family of foliations using a
![]() $C^\infty $
-smooth h-flat function
$C^\infty $
-smooth h-flat function
![]() $\psi (s,h)$
on
$\psi (s,h)$
on
![]() $S^1\times {\mathbb R}_{\geq 0}$
,
$S^1\times {\mathbb R}_{\geq 0}$
,
![]() $S^1={\mathbb R}_s / {\mathbb Z}$
, with non-trivial germ at
$S^1={\mathbb R}_s / {\mathbb Z}$
, with non-trivial germ at
![]() $S^1\times \{0\}$
, as in equation (2.44). Namely, set
$S^1\times \{0\}$
, as in equation (2.44). Namely, set
 $$ \begin{align*} g_{\varepsilon} (\tau,h):=h+{\varepsilon} \chi(\tau,h),\quad \chi(\tau,h):=\psi \bigg(\frac{\tau}{\sqrt h},h\bigg), \quad{\varepsilon} \in[0,1]. \end{align*} $$
$$ \begin{align*} g_{\varepsilon} (\tau,h):=h+{\varepsilon} \chi(\tau,h),\quad \chi(\tau,h):=\psi \bigg(\frac{\tau}{\sqrt h},h\bigg), \quad{\varepsilon} \in[0,1]. \end{align*} $$
The functions
![]() $g_{\varepsilon } $
are F-invariant and
$g_{\varepsilon } $
are F-invariant and
![]() $g_{\varepsilon } (\tau ,h)=h+{\operatorname {flat}}(h)$
. The germs of any two foliations
$g_{\varepsilon } (\tau ,h)=h+{\operatorname {flat}}(h)$
. The germs of any two foliations
![]() $g_{{\varepsilon } _1}=\mathrm {const.}$
,
$g_{{\varepsilon } _1}=\mathrm {const.}$
,
![]() $g_{{\varepsilon } _2}=\mathrm {const.}$
,
$g_{{\varepsilon } _2}=\mathrm {const.}$
,
![]() ${\varepsilon } _1\neq {\varepsilon } _2$
, are distinct at each point in J, by Theorem 1.35 and Proposition 1.36. It remains to prove their regularity and regularity of the dual foliations by caustics on one and the same domain. To do this, we use the following claim.
${\varepsilon } _1\neq {\varepsilon } _2$
, are distinct at each point in J, by Theorem 1.35 and Proposition 1.36. It remains to prove their regularity and regularity of the dual foliations by caustics on one and the same domain. To do this, we use the following claim.
Claim 6. Shrinking the domain W adjacent to
![]() $J=\gamma ^*$
, one can achieve that for every
$J=\gamma ^*$
, one can achieve that for every
![]() ${\varepsilon } \in [0,1]$
, the foliation
${\varepsilon } \in [0,1]$
, the foliation
![]() $g_{\varepsilon } =\mathrm {const.}$
is regular on
$g_{\varepsilon } =\mathrm {const.}$
is regular on
![]() $W\cup J$
, its leaves are strictly convex curves, as is
$W\cup J$
, its leaves are strictly convex curves, as is
![]() $\gamma ^*$
, and the map
$\gamma ^*$
, and the map
![]() ${\Lambda } _{\varepsilon } :x\to L_{x,{\varepsilon } }$
sending a point
${\Lambda } _{\varepsilon } :x\to L_{x,{\varepsilon } }$
sending a point
![]() $x\in W$
to the projective line
$x\in W$
to the projective line
![]() $L_{x,{\varepsilon } }$
tangent to the level curve
$L_{x,{\varepsilon } }$
tangent to the level curve
![]() $\{ g_{\varepsilon } =g_{\varepsilon } (x)\}$
at x is a diffeomorphism on W.
$\{ g_{\varepsilon } =g_{\varepsilon } (x)\}$
at x is a diffeomorphism on W.
Proof. Consider the function h and the above function
![]() $\chi $
as functions on
$\chi $
as functions on
![]() $W\cup \gamma ^*$
as on a subset in
$W\cup \gamma ^*$
as on a subset in
![]() ${\mathbb R}^2\subset {\mathbb {RP}}^2$
. The curve
${\mathbb R}^2\subset {\mathbb {RP}}^2$
. The curve
![]() $\gamma ^*=\{ h=0\}$
is strictly convex. Hence, shrinking W, we can and will consider that each level curve
$\gamma ^*=\{ h=0\}$
is strictly convex. Hence, shrinking W, we can and will consider that each level curve
![]() $\{ h=\mathrm {const.}\}\cap W$
is strictly convex. Consider the rectangles
$\{ h=\mathrm {const.}\}\cap W$
is strictly convex. Consider the rectangles
![]() $\Pi _k\subset W$
from the proof of the above Claim 5 (in the coordinates
$\Pi _k\subset W$
from the proof of the above Claim 5 (in the coordinates
![]() $(\tau ,h)$
) with decreasing heights. They are represented as curvilinear quadrilaterals in
$(\tau ,h)$
) with decreasing heights. They are represented as curvilinear quadrilaterals in
![]() ${\mathbb R}^2\subset {\mathbb {RP}}^2$
. Choosing them with heights small enough, we can achieve that
${\mathbb R}^2\subset {\mathbb {RP}}^2$
. Choosing them with heights small enough, we can achieve that
![]() $\lVert \nabla \chi \rVert < \tfrac 12 \lVert \nabla h\rVert $
on
$\lVert \nabla \chi \rVert < \tfrac 12 \lVert \nabla h\rVert $
on
![]() $\Pi _k$
. Let us now replace W by
$\Pi _k$
. Let us now replace W by
![]() $\bigcup _k\Pi _k$
. Then,
$\bigcup _k\Pi _k$
. Then,
![]() $\nabla g_{\varepsilon } \neq 0$
on W, and hence, the foliation
$\nabla g_{\varepsilon } \neq 0$
on W, and hence, the foliation
![]() ${g_{\varepsilon } =\mathrm {const.}}$
is regular for all
${g_{\varepsilon } =\mathrm {const.}}$
is regular for all
![]() ${\varepsilon } \in [0,1]$
. Choosing
${\varepsilon } \in [0,1]$
. Choosing
![]() $\Pi _k$
with heights small enough (step by step), one can also achieve that each level curve
$\Pi _k$
with heights small enough (step by step), one can also achieve that each level curve
![]() $\{ g_{\varepsilon } =\mathrm {const.}\}\cap \Pi _k$
be strictly convex for every
$\{ g_{\varepsilon } =\mathrm {const.}\}\cap \Pi _k$
be strictly convex for every
![]() ${\varepsilon } \in [0,1]$
, by strict convexity of the boundary curve
${\varepsilon } \in [0,1]$
, by strict convexity of the boundary curve
![]() $\gamma ^*$
and h-flatness of the function
$\gamma ^*$
and h-flatness of the function
![]() $\psi $
. In more detail, let
$\psi $
. In more detail, let
![]() $(x,y)$
be coordinates on the ambient affine chart
$(x,y)$
be coordinates on the ambient affine chart
![]() ${\mathbb R}^2$
. Strict convexity of level curves
${\mathbb R}^2$
. Strict convexity of level curves
![]() $\{g_{\varepsilon } =\mathrm {const.}\}$
is equivalent to non-vanishing of the Hessian
$\{g_{\varepsilon } =\mathrm {const.}\}$
is equivalent to non-vanishing of the Hessian
![]() $H(g_{\varepsilon })$
:
$H(g_{\varepsilon })$
:
 $$ \begin{align*} H(g_{\varepsilon} )\neq0,\quad H(g):=\frac{\partial^2g}{\partial x^2}\bigg(\frac{\partial g}{\partial y}\bigg)^2 + \frac{\partial^2g}{\partial y^2}\bigg(\frac{\partial g}{\partial x}\bigg)^2-2 \frac{\partial^2g}{\partial x\partial y}\bigg(\frac{\partial g}{\partial x}\bigg)\bigg(\frac{\partial g}{\partial y}\bigg). \end{align*} $$
$$ \begin{align*} H(g_{\varepsilon} )\neq0,\quad H(g):=\frac{\partial^2g}{\partial x^2}\bigg(\frac{\partial g}{\partial y}\bigg)^2 + \frac{\partial^2g}{\partial y^2}\bigg(\frac{\partial g}{\partial x}\bigg)^2-2 \frac{\partial^2g}{\partial x\partial y}\bigg(\frac{\partial g}{\partial x}\bigg)\bigg(\frac{\partial g}{\partial y}\bigg). \end{align*} $$
(The Hessian
![]() $H(g)$
of a function g was introduced by Tabachnikov in his paper [Reference Tabachnikov21], where he used it to study his conjecture stating that every polynomially integrable outer billiard is an ellipse (later this conjecture was solved in [Reference Glutsyuk and Shustin11]). The Hessian was also used by Bialy, Mironov, and later the author in the solution of Bolotin’s polynomial version of the Birkhoff conjecture, which is the result of papers [Reference Bialy and Mironov5, Reference Bialy and Mironov6, Reference Glutsyuk9].)
$H(g)$
of a function g was introduced by Tabachnikov in his paper [Reference Tabachnikov21], where he used it to study his conjecture stating that every polynomially integrable outer billiard is an ellipse (later this conjecture was solved in [Reference Glutsyuk and Shustin11]). The Hessian was also used by Bialy, Mironov, and later the author in the solution of Bolotin’s polynomial version of the Birkhoff conjecture, which is the result of papers [Reference Bialy and Mironov5, Reference Bialy and Mironov6, Reference Glutsyuk9].)
The Hessian
![]() $H(g_{\varepsilon } )$
is the sum of the Hessian
$H(g_{\varepsilon } )$
is the sum of the Hessian
![]() $H(h)$
(which is non-zero on
$H(h)$
(which is non-zero on
![]() $W\cup \gamma ^*$
, since the curves
$W\cup \gamma ^*$
, since the curves
![]() $\{h=\mathrm {const.}\}$
are strictly convex) and a finite sum of products; each product contains
$\{h=\mathrm {const.}\}$
are strictly convex) and a finite sum of products; each product contains
![]() ${\varepsilon } $
, at least one derivative of the function
${\varepsilon } $
, at least one derivative of the function
![]() $\chi $
, at most two derivatives of the function h, at most two derivatives of the function
$\chi $
, at most two derivatives of the function h, at most two derivatives of the function
![]() $\tau $
; each derivative is of order at most two. Choosing the rectangles
$\tau $
; each derivative is of order at most two. Choosing the rectangles
![]() $\Pi _k$
with heights small enough, we can achieve that the module of the latter sum of products be no greater than
$\Pi _k$
with heights small enough, we can achieve that the module of the latter sum of products be no greater than
![]() $\tfrac 12{\varepsilon } \lvert H(h)\rvert $
for
$\tfrac 12{\varepsilon } \lvert H(h)\rvert $
for
![]() ${\varepsilon } \in [0,1]$
. This follows from convexity of the curve
${\varepsilon } \in [0,1]$
. This follows from convexity of the curve
![]() $\gamma ^*$
and h-flatness of the function
$\gamma ^*$
and h-flatness of the function
![]() $\psi $
: shrinking W, one can achieve that all the first and second derivatives of the function
$\psi $
: shrinking W, one can achieve that all the first and second derivatives of the function
![]() $\chi $
have moduli bounded by arbitrarily small
$\chi $
have moduli bounded by arbitrarily small
![]() $\delta $
(Claim 5). Then
$\delta $
(Claim 5). Then
![]() $H(g_{\varepsilon } )\neq 0$
on W, hence, the curves
$H(g_{\varepsilon } )\neq 0$
on W, hence, the curves
![]() $\{ g_{\varepsilon } =\mathrm {const.}\}\cap W$
are strictly convex.
$\{ g_{\varepsilon } =\mathrm {const.}\}\cap W$
are strictly convex.
Now for every k, we choose smaller rectangles
![]() $\widetilde {\Pi }_k\subset \Pi _k$
with decreasing heights and with the lateral (that is, vertical) sides lying in the lateral sides of the bigger rectangles
$\widetilde {\Pi }_k\subset \Pi _k$
with decreasing heights and with the lateral (that is, vertical) sides lying in the lateral sides of the bigger rectangles
![]() $\Pi _k$
that satisfy the following additional statement. For every
$\Pi _k$
that satisfy the following additional statement. For every
![]() ${\varepsilon } \in [0,1]$
, let
${\varepsilon } \in [0,1]$
, let
![]() $\Pi _{k,{\varepsilon } }$
denote the minimal flowbox for the foliation
$\Pi _{k,{\varepsilon } }$
denote the minimal flowbox for the foliation
![]() $g_{\varepsilon } =\mathrm {const.}$
with lateral (that is, transversal) sides lying in the lateral sides of
$g_{\varepsilon } =\mathrm {const.}$
with lateral (that is, transversal) sides lying in the lateral sides of
![]() $\Pi _k$
that contains
$\Pi _k$
that contains
![]() $\widetilde {\Pi }_k$
. This is the union of arcs of leaves that go from one lateral side of
$\widetilde {\Pi }_k$
. This is the union of arcs of leaves that go from one lateral side of
![]() $\Pi _k$
to the other one and cross
$\Pi _k$
to the other one and cross
![]() $\widetilde {\Pi }_k$
. For every k, we can and will subsequently choose
$\widetilde {\Pi }_k$
. For every k, we can and will subsequently choose
![]() $\widetilde {\Pi }_k$
with heights small enough (that is, narrow enough in the transversal direction) so that for every
$\widetilde {\Pi }_k$
with heights small enough (that is, narrow enough in the transversal direction) so that for every
![]() ${\varepsilon } \in [0,1]$
, the flowbox
${\varepsilon } \in [0,1]$
, the flowbox
![]() $\Pi _{k,{\varepsilon } }$
exists, lies in
$\Pi _{k,{\varepsilon } }$
exists, lies in
![]() $\Pi _k$
, and the heights of the flowboxes
$\Pi _k$
, and the heights of the flowboxes
![]() $\Pi _{k,{\varepsilon } }$
be decreasing in k: more precisely, for every k, each local leaf in
$\Pi _{k,{\varepsilon } }$
be decreasing in k: more precisely, for every k, each local leaf in
![]() $\Pi _{k+1,{\varepsilon } }$
crosses
$\Pi _{k+1,{\varepsilon } }$
crosses
![]() $\Pi _{k,{\varepsilon } }$
, as in the proof of Proposition 2.22. Then the map
$\Pi _{k,{\varepsilon } }$
, as in the proof of Proposition 2.22. Then the map
![]() ${\Lambda } _{\varepsilon } :x\mapsto L_{x,{\varepsilon } }$
is a diffeomorphism on
${\Lambda } _{\varepsilon } :x\mapsto L_{x,{\varepsilon } }$
is a diffeomorphism on
![]() $W_{\varepsilon } :=\bigcup _k\Pi _{k,{\varepsilon } }$
for every
$W_{\varepsilon } :=\bigcup _k\Pi _{k,{\varepsilon } }$
for every
![]() ${\varepsilon } \in [0,1]$
, as at the end of the proof of Proposition 2.22. Hence, it is a diffeomorphism on
${\varepsilon } \in [0,1]$
, as at the end of the proof of Proposition 2.22. Hence, it is a diffeomorphism on
The claim is proved.
Claim 7. Consider the foliation by caustics of the billiard on
![]() $\gamma $
that is dual to the foliation
$\gamma $
that is dual to the foliation
![]() $g_{\varepsilon } =\mathrm {const.}$
. There exists a domain
$g_{\varepsilon } =\mathrm {const.}$
. There exists a domain
![]() $U\subset {\mathbb R}^2$
adjacent to
$U\subset {\mathbb R}^2$
adjacent to
![]() $\gamma $
from the convex side where the above foliation by caustics is
$\gamma $
from the convex side where the above foliation by caustics is
![]() $C^{\infty }$
-smooth (and also smooth at the points of the curve
$C^{\infty }$
-smooth (and also smooth at the points of the curve
![]() $\gamma $
) for every
$\gamma $
) for every
![]() ${\varepsilon } \in [0,1]$
. Moreover, shrinking U, one can achieve that for every
${\varepsilon } \in [0,1]$
. Moreover, shrinking U, one can achieve that for every
![]() $x\in \gamma $
and every
$x\in \gamma $
and every
![]() ${\varepsilon } \in [0,1]$
, there are at most two tangent lines through x to any given leaf of the corresponding foliation by caustics on U.
${\varepsilon } \in [0,1]$
, there are at most two tangent lines through x to any given leaf of the corresponding foliation by caustics on U.
Proof. Let
![]() $\widetilde {W}$
be the domain in equation (2.48) constructed above. For every
$\widetilde {W}$
be the domain in equation (2.48) constructed above. For every
![]() ${\varepsilon } \in [0,1]$
, the map
${\varepsilon } \in [0,1]$
, the map
![]() ${\Lambda } _{\varepsilon } ^*:x\mapsto L_{x,{\varepsilon } }^*$
sending x to the point dual to the corresponding line
${\Lambda } _{\varepsilon } ^*:x\mapsto L_{x,{\varepsilon } }^*$
sending x to the point dual to the corresponding line
![]() $L_{x,{\varepsilon } }$
is a diffeomorphism, since so is
$L_{x,{\varepsilon } }$
is a diffeomorphism, since so is
![]() ${\Lambda } _{\varepsilon } $
. It sends the domain
${\Lambda } _{\varepsilon } $
. It sends the domain
![]() $\widetilde {W}$
foliated by level curves of the function
$\widetilde {W}$
foliated by level curves of the function
![]() $g_{\varepsilon } $
onto a domain
$g_{\varepsilon } $
onto a domain
![]() $U_{\varepsilon } $
adjacent to
$U_{\varepsilon } $
adjacent to
![]() $\gamma $
and foliated by their dual curves: caustics of the billiard on
$\gamma $
and foliated by their dual curves: caustics of the billiard on
![]() $\gamma $
. They form a
$\gamma $
. They form a
![]() $C^\infty $
-smooth foliation on
$C^\infty $
-smooth foliation on
![]() $U_{\varepsilon } \cup \gamma $
. For the proof of the first statement of Claim 7, it remains to show that there exists a domain U adjacent to
$U_{\varepsilon } \cup \gamma $
. For the proof of the first statement of Claim 7, it remains to show that there exists a domain U adjacent to
![]() $\gamma $
that lies in the intersection
$\gamma $
that lies in the intersection
![]() $\bigcap _{\varepsilon } U_{\varepsilon } $
(and hence, for each
$\bigcap _{\varepsilon } U_{\varepsilon } $
(and hence, for each
![]() ${\varepsilon } $
, it is smoothly foliated by the corresponding caustics). To do this, we construct the above
${\varepsilon } $
, it is smoothly foliated by the corresponding caustics). To do this, we construct the above
![]() $\widetilde {W}$
and a smaller domain
$\widetilde {W}$
and a smaller domain
![]() $W'\subset \widetilde {W}$
adjacent to
$W'\subset \widetilde {W}$
adjacent to
![]() $\gamma ^*$
so that the following statement holds:
$\gamma ^*$
so that the following statement holds:
(*) for every
![]() $p\in W'$
and every
$p\in W'$
and every
![]() ${\varepsilon } \in [0,1]$
, there exists a
${\varepsilon } \in [0,1]$
, there exists a
![]() $q=q(p,{\varepsilon } )\in \widetilde {W}$
such that the projective line
$q=q(p,{\varepsilon } )\in \widetilde {W}$
such that the projective line
![]() $L_{p,0}$
tangent to the curve
$L_{p,0}$
tangent to the curve
![]() $\{ h=h(p)\}$
at p is tangent to the leaf of the foliation
$\{ h=h(p)\}$
at p is tangent to the leaf of the foliation
![]() $g_{\varepsilon } =\mathrm {const.}$
at q.
$g_{\varepsilon } =\mathrm {const.}$
at q.
Statement (*) implies that the image
![]() $U={\Lambda } _0(W')$
is contained in all the domains
$U={\Lambda } _0(W')$
is contained in all the domains
![]() $U_{\varepsilon } $
and regularly foliated by caustics dual to level curves of the function
$U_{\varepsilon } $
and regularly foliated by caustics dual to level curves of the function
![]() $g_{\varepsilon } $
for every
$g_{\varepsilon } $
for every
![]() ${\varepsilon } \in [0,1]$
.
${\varepsilon } \in [0,1]$
.
Take the rectangles
![]() $\Pi _k$
and
$\Pi _k$
and
![]() $\widetilde {\Pi }_k$
from the proof of Claim 6. Let us call their sections
$\widetilde {\Pi }_k$
from the proof of Claim 6. Let us call their sections
![]() ${h=\mathrm {const.}}$
horizontal and transversal sections
${h=\mathrm {const.}}$
horizontal and transversal sections
![]() $\tau =\mathrm {const.}$
vertical. For every k, fix two vertical sections
$\tau =\mathrm {const.}$
vertical. For every k, fix two vertical sections
![]() $\ell _{1,k}$
and
$\ell _{1,k}$
and
![]() $\ell _{2,k}$
crossing the interior
$\ell _{2,k}$
crossing the interior
![]() $\operatorname {Int}(\Pi _k)$
that lie in the
$\operatorname {Int}(\Pi _k)$
that lie in the
![]() $1/{2^k}$
-neighborhoods of the corresponding lateral sides of the rectangle
$1/{2^k}$
-neighborhoods of the corresponding lateral sides of the rectangle
![]() $\Pi _k$
. We can and will choose a rectangle
$\Pi _k$
. We can and will choose a rectangle
![]() $\Pi _k'\subset \widetilde {\Pi }_k$
with lateral sides lying on
$\Pi _k'\subset \widetilde {\Pi }_k$
with lateral sides lying on
![]() $\ell _{1,k}$
and
$\ell _{1,k}$
and
![]() $\ell _{2,k}$
, and height small enough so that for every
$\ell _{2,k}$
, and height small enough so that for every
![]() ${\varepsilon } \in [0,1]$
and every
${\varepsilon } \in [0,1]$
and every
![]() $p\in \Pi _k'$
, there exists a
$p\in \Pi _k'$
, there exists a
![]() $q=q(p,{\varepsilon } )\in \widetilde {\Pi }_k$
satisfying statement (*). This is possible by flatness of the function
$q=q(p,{\varepsilon } )\in \widetilde {\Pi }_k$
satisfying statement (*). This is possible by flatness of the function
![]() $\psi $
and strict convexity of the curve
$\psi $
and strict convexity of the curve
![]() $\gamma ^*$
. Then statement (*) holds for the domain
$\gamma ^*$
. Then statement (*) holds for the domain
![]() $W'=\bigcup _k\Pi _k'\subset W$
. This together with the above discussion proves the first statement of Claim 7. One can achieve that its second statement (on tangent lines) holds as well by choosing the above rectangles
$W'=\bigcup _k\Pi _k'\subset W$
. This together with the above discussion proves the first statement of Claim 7. One can achieve that its second statement (on tangent lines) holds as well by choosing the above rectangles
![]() $\Pi _k'$
with height small enough, as in the proof of the existence in Theorem 1.9 at the end of §2.7.
$\Pi _k'$
with height small enough, as in the proof of the existence in Theorem 1.9 at the end of §2.7.
Claim 7 implies non-uniqueness statement (1) of Theorem 1.9 (the case when
![]() $\gamma $
is an unbounded one-dimensional submanifold), with one-dimensional family of foliations with distinct germs. Modifying the above arguments as in the proof of non-uniqueness statement of Theorem 1.30 (see equation (2.47) and the discussion after it), we get an N-dimensional family of foliations with distinct germs for every
$\gamma $
is an unbounded one-dimensional submanifold), with one-dimensional family of foliations with distinct germs. Modifying the above arguments as in the proof of non-uniqueness statement of Theorem 1.30 (see equation (2.47) and the discussion after it), we get an N-dimensional family of foliations with distinct germs for every
![]() $N\in {\mathbb N}$
. Non-uniqueness statement (2) of Theorem 1.9 is proved analogously, with small modifications analogous to those mentioned at the end of §2.7. Non-uniqueness statements of Theorems 1.12 and 1.13 are proved analogously.
$N\in {\mathbb N}$
. Non-uniqueness statement (2) of Theorem 1.9 is proved analogously, with small modifications analogous to those mentioned at the end of §2.7. Non-uniqueness statements of Theorems 1.12 and 1.13 are proved analogously.
2.10 Conjugacy of billiard maps and Lazutkin length. Proof of Theorems 1.39, 1.40, 1.43, and 1.44, Propositions 1.45 and 1.46, and Lemma 1.47
Proof of Proposition 1.45
The map
 $$ \begin{align*} (s,y)\mapsto(X,Y):=(t_L(s),w^{2/3}(s)y),\quad t_L(s)=\int_{s_0}^sw^{-(2/3)}(u)\,du \end{align*} $$
$$ \begin{align*} (s,y)\mapsto(X,Y):=(t_L(s),w^{2/3}(s)y),\quad t_L(s)=\int_{s_0}^sw^{-(2/3)}(u)\,du \end{align*} $$
is symplectic and conjugates F to a
![]() $C^\infty $
-lifted strongly billiard-like map of the type
$C^\infty $
-lifted strongly billiard-like map of the type
see [Reference Glutsyuk10, Theorem 7.11] and Proposition 1.24. (This statement is implicitly contained in [Reference Lazutkin15, Reference Marvizi and Melrose16].) Thus, without loss of generality, we can and will consider that F has the form in equation (2.49), hence,
![]() $w(s)\equiv 1$
. Then,
$w(s)\equiv 1$
. Then,
![]() $t_L(s)=s$
up to additive constant. Thus, we have to show that
$t_L(s)=s$
up to additive constant. Thus, we have to show that
By definition,
![]() $H(s,y)=(H_1(s,y),H_2(s,y))$
conjugates F to
$H(s,y)=(H_1(s,y),H_2(s,y))$
conjugates F to
![]() ${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
. Hence, it sends the fixed point line
${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
. Hence, it sends the fixed point line
![]() $\{ y=0\}$
of the map F to the fixed point line
$\{ y=0\}$
of the map F to the fixed point line
![]() $\{ z=0\}$
of the map
$\{ z=0\}$
of the map
![]() ${\Lambda } $
, thus,
${\Lambda } $
, thus,
![]() $H_2(s,0)\equiv 0$
. Writing conjugacy equation on the first components yields
$H_2(s,0)\equiv 0$
. Writing conjugacy equation on the first components yields
 $$ \begin{align*} H_1\circ F(s,y) &=H_1(s+\sqrt y+O(y), y+o(y^{3/2}))=H_1(s,0)+\frac{\partial H_1}{\partial s}(s,0)\sqrt y+O(y) \\ &={\Lambda}_1\circ H(s,y)=H_1(s,y)+\sqrt{H_2(s,y)}=H_1(s,0)\\&\quad+\sqrt{\frac{\partial H_2}{\partial y}(s,0)}\sqrt y+O(y). \end{align*} $$
$$ \begin{align*} H_1\circ F(s,y) &=H_1(s+\sqrt y+O(y), y+o(y^{3/2}))=H_1(s,0)+\frac{\partial H_1}{\partial s}(s,0)\sqrt y+O(y) \\ &={\Lambda}_1\circ H(s,y)=H_1(s,y)+\sqrt{H_2(s,y)}=H_1(s,0)\\&\quad+\sqrt{\frac{\partial H_2}{\partial y}(s,0)}\sqrt y+O(y). \end{align*} $$
This yields
 $$ \begin{align} \frac{\partial H_1}{\partial s}(s,0)\equiv \sqrt{\frac{\partial H_2}{\partial y}(s,0)}>0. \end{align} $$
$$ \begin{align} \frac{\partial H_1}{\partial s}(s,0)\equiv \sqrt{\frac{\partial H_2}{\partial y}(s,0)}>0. \end{align} $$
The Jacobian matrix of the map H at points
![]() $(s,0)$
is equal to
$(s,0)$
is equal to
 $$ \begin{align} \mathrm{Jac}(s,0)=\frac{\partial H_1}{\partial s}(s,0)\frac{\partial H_2}{\partial y}(s,0)=\bigg(\frac{\partial H_1}{\partial s}(s,0)\bigg)^3>0, \end{align} $$
$$ \begin{align} \mathrm{Jac}(s,0)=\frac{\partial H_1}{\partial s}(s,0)\frac{\partial H_2}{\partial y}(s,0)=\bigg(\frac{\partial H_1}{\partial s}(s,0)\bigg)^3>0, \end{align} $$
by equation (2.52) and since
![]() $H_2(s,0)\equiv 0$
, which yields
$H_2(s,0)\equiv 0$
, which yields
![]() ${\partial H_2}/{\partial s}(s,0)=0$
. This proves orientation-preserving property of the diffeomorphism H and increasing of the function
${\partial H_2}/{\partial s}(s,0)=0$
. This proves orientation-preserving property of the diffeomorphism H and increasing of the function
![]() $H_1(s,0)$
.
$H_1(s,0)$
.
Now let H be symplectic, that is,
![]() $\mathrm {Jac}(s,0)\equiv 1$
. Then
$\mathrm {Jac}(s,0)\equiv 1$
. Then
![]() ${\partial H_1}(s,0)/{\partial s}\equiv 1$
, by equation (2.53). This means that
${\partial H_1}(s,0)/{\partial s}\equiv 1$
, by equation (2.53). This means that
![]() $H_1(s,0)=s+\beta $
for some
$H_1(s,0)=s+\beta $
for some
![]() $\beta \in {\mathbb R}$
. This proves equation (2.51), that is, equation (1.20).
$\beta \in {\mathbb R}$
. This proves equation (2.51), that is, equation (1.20).
Now let H be not necessarily symplectic. Let us prove equation (2.50), that is, equation (1.21). Suppose the contrary: there exist two points
![]() $s_0<s^*_0\in (a,b)$
such that
$s_0<s^*_0\in (a,b)$
such that
Fix small
![]() ${\varepsilon } ,\delta>0$
such that
${\varepsilon } ,\delta>0$
such that
Fix a small
![]() $\eta>0$
and a
$\eta>0$
and a
![]() $y_0\in (0, \eta /4)$
, set
$y_0\in (0, \eta /4)$
, set
![]() $q_0=(s_0,y_0)$
. Let
$q_0=(s_0,y_0)$
. Let
![]() $q_{-N_-},\ldots , q_{-1},q_0$
,
$q_{-N_-},\ldots , q_{-1},q_0$
,
![]() $q_1,\ldots ,q_{N_+}$
,
$q_1,\ldots ,q_{N_+}$
,
![]() $q_j=(s_j,y_j)$
, denote the F-orbit of the point
$q_j=(s_j,y_j)$
, denote the F-orbit of the point
![]() $q_0$
in the rectangle
$q_0$
in the rectangle
![]() $[s_0-{\varepsilon } ,s_0^*+{\varepsilon } ]\times [0,\eta ]$
. Here,
$[s_0-{\varepsilon } ,s_0^*+{\varepsilon } ]\times [0,\eta ]$
. Here,
![]() $N_\pm =N_\pm (q_0)$
. It is known that the s-coordinates of its points form an asymptotic arithmetic progression
$N_\pm =N_\pm (q_0)$
. It is known that the s-coordinates of its points form an asymptotic arithmetic progression
![]() $s_j=s(q_j)$
, and their y-coordinates are asymptotically equivalent:
$s_j=s(q_j)$
, and their y-coordinates are asymptotically equivalent:
uniformly in
![]() $j\in [-N_-(y_0),N_+(y_0)-1]$
,
$j\in [-N_-(y_0),N_+(y_0)-1]$
,
whenever
![]() $y_0$
is small enough (depending on
$y_0$
is small enough (depending on
![]() ${\varepsilon } $
). See [Reference Glutsyuk10, Lemma 7.13]. The image of the above orbit under the map H should be an orbit of the map
${\varepsilon } $
). See [Reference Glutsyuk10, Lemma 7.13]. The image of the above orbit under the map H should be an orbit of the map
![]() ${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
. The abscissas of its points,
${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
. The abscissas of its points,
![]() $t_j:=H_1(q_j)$
, form an arithmetic progression:
$t_j:=H_1(q_j)$
, form an arithmetic progression:
![]() $t_{j+1}-t_j=\sqrt {z_0}$
,
$t_{j+1}-t_j=\sqrt {z_0}$
,
![]() $z_0=z(H(q_0))$
. We claim that this yields a contradiction to the inequality
$z_0=z(H(q_0))$
. We claim that this yields a contradiction to the inequality
![]() $\ell \neq \ell ^*$
and equation (2.54). Indeed, one has
$\ell \neq \ell ^*$
and equation (2.54). Indeed, one has
by equation (2.54) and the Lagrange increment theorem. However, take a family of indices
![]() $k=k(y_0)$
such that
$k=k(y_0)$
such that
![]() $s_k=s_k(y_0)\to s_0^*$
, as
$s_k=s_k(y_0)\to s_0^*$
, as
![]() $y_0\to 0$
: it exists, since the asymptotic progression
$y_0\to 0$
: it exists, since the asymptotic progression
![]() $s_j$
has steps uniformly decreasing to
$s_j$
has steps uniformly decreasing to
![]() $0$
, it starts on the left from
$0$
, it starts on the left from
![]() $s_0$
and ends on the right from
$s_0$
and ends on the right from
![]() $s_0^*>s_0$
, see equation (2.55). Repeating the above argument for
$s_0^*>s_0$
, see equation (2.55). Repeating the above argument for
![]() $t_k$
and
$t_k$
and
![]() $t_{k+1}$
yields
$t_{k+1}$
yields
Hence,
![]() $t_{k+1}-t_k\neq t_1-t_0$
, whenever
$t_{k+1}-t_k\neq t_1-t_0$
, whenever
![]() $y_0$
is small enough, since
$y_0$
is small enough, since
![]() $\ell \neq \ell ^*$
. The contradiction thus obtained to the equality of the above differences proves that
$\ell \neq \ell ^*$
. The contradiction thus obtained to the equality of the above differences proves that
![]() ${\partial H_1}(s,0)/{\partial s}\equiv \mathrm {const}$
. This proves equation (2.50) and Proposition 1.45.
${\partial H_1}(s,0)/{\partial s}\equiv \mathrm {const}$
. This proves equation (2.50) and Proposition 1.45.
Proof of Theorem 1.44
Let us fix an arbitrary point in each curve
![]() $\gamma _i$
and parameterize it by natural length parameter so that the given point corresponds to zero parameter value. For every
$\gamma _i$
and parameterize it by natural length parameter so that the given point corresponds to zero parameter value. For every
![]() $i=1,2$
, let
$i=1,2$
, let
![]() ${\mathcal T}_{\gamma _i}$
denote the billiard map corresponding to the curve
${\mathcal T}_{\gamma _i}$
denote the billiard map corresponding to the curve
![]() $\gamma _i$
. It is a
$\gamma _i$
. It is a
![]() $C^\infty $
-lifted strongly billiard-like map in the coordinates
$C^\infty $
-lifted strongly billiard-like map in the coordinates
![]() $(s,y)$
defined on a domain in
$(s,y)$
defined on a domain in
![]() ${\mathbb R}\times {\mathbb R}_+$
adjacent to an interval
${\mathbb R}\times {\mathbb R}_+$
adjacent to an interval
![]() $J_{\gamma _i}=(a_i,b_i)\times \{0\}$
; here
$J_{\gamma _i}=(a_i,b_i)\times \{0\}$
; here
![]() $(a_i,b_i)$
is the length parameter interval parameterizing
$(a_i,b_i)$
is the length parameter interval parameterizing
![]() $\gamma _i$
. The corresponding function
$\gamma _i$
. The corresponding function
![]() $w=w_i(s)$
is equal to
$w=w_i(s)$
is equal to
![]() $2\sqrt 2\kappa _i^{-1}(s)$
, where
$2\sqrt 2\kappa _i^{-1}(s)$
, where
![]() $\kappa _i$
is the curvature of the curve
$\kappa _i$
is the curvature of the curve
![]() $\gamma _i$
. There exists a domain
$\gamma _i$
. There exists a domain
![]() $U_i\subset {\mathbb R}_s\times ({\mathbb R}_+)_y$
adjacent to
$U_i\subset {\mathbb R}_s\times ({\mathbb R}_+)_y$
adjacent to
![]() $J_{\gamma _i}$
such that there exists a
$J_{\gamma _i}$
such that there exists a
![]() $C^\infty $
-smooth symplectomorphism
$C^\infty $
-smooth symplectomorphism
![]() $H_i=(H_{1i},H_{2i})$
on
$H_i=(H_{1i},H_{2i})$
on
![]() $U_i\cup J_{\gamma _i}$
conjugating
$U_i\cup J_{\gamma _i}$
conjugating
![]() ${\mathcal T}_{\gamma _i}$
to its normal form
${\mathcal T}_{\gamma _i}$
to its normal form
![]() ${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
,
${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
,
![]() $H_i\circ {\mathcal T}_{\gamma _i}\circ H_i^{-1}={\Lambda } $
(Theorem 1.27). The restriction to the s-axis of the first component
$H_i\circ {\mathcal T}_{\gamma _i}\circ H_i^{-1}={\Lambda } $
(Theorem 1.27). The restriction to the s-axis of the first component
![]() $H_{1i}$
is given by the Lazutkin parameter:
$H_{1i}$
is given by the Lazutkin parameter:
by Proposition 1.45. Therefore, the image
![]() $H_{1i}(J_{\gamma _i})$
is the interval
$H_{1i}(J_{\gamma _i})$
is the interval
![]() $\widetilde {J}_i\times \{0\}$
equipped with the coordinate
$\widetilde {J}_i\times \{0\}$
equipped with the coordinate
![]() $t_L$
, whose length is thus equal to
$t_L$
, whose length is thus equal to
![]() $\tfrac 1{2}{\mathcal L}(\gamma _i)$
. The image domain
$\tfrac 1{2}{\mathcal L}(\gamma _i)$
. The image domain
![]() $H_i(U_i)\subset {\mathbb R}\times {\mathbb R}_+$
is adjacent to
$H_i(U_i)\subset {\mathbb R}\times {\mathbb R}_+$
is adjacent to
![]() $\widetilde {J}_i$
. Thus, (symplectic)
$\widetilde {J}_i$
. Thus, (symplectic)
![]() $C^\infty $
-conjugacy of the billiard maps near the boundary is equivalent to the existence of a (symplectic)
$C^\infty $
-conjugacy of the billiard maps near the boundary is equivalent to the existence of a (symplectic)
![]() $C^\infty $
-diffeomorphism
$C^\infty $
-diffeomorphism
![]() $\Phi $
commuting with
$\Phi $
commuting with
![]() ${\Lambda } $
, defined on a domain
${\Lambda } $
, defined on a domain
![]() $V_1\subset {\mathbb R}_t\times ({\mathbb R}_+)_z$
adjacent to
$V_1\subset {\mathbb R}_t\times ({\mathbb R}_+)_z$
adjacent to
![]() $\widetilde {J}_1$
and sending it onto a domain
$\widetilde {J}_1$
and sending it onto a domain
![]() $V_2\subset {\mathbb R}_t\times ({\mathbb R}_+)_z$
adjacent to
$V_2\subset {\mathbb R}_t\times ({\mathbb R}_+)_z$
adjacent to
![]() $\widetilde {J}_2$
that extends as a
$\widetilde {J}_2$
that extends as a
![]() $C^\infty $
-diffeomorphism to
$C^\infty $
-diffeomorphism to
![]() $\widetilde {J}_1$
,
$\widetilde {J}_1$
,
![]() $\Phi (\widetilde {J}_1)=\widetilde {J}_2$
. The latter diffeomorphism
$\Phi (\widetilde {J}_1)=\widetilde {J}_2$
. The latter diffeomorphism
![]() $\Phi $
exists in the class of symplectomorphisms if and only if
$\Phi $
exists in the class of symplectomorphisms if and only if
![]() ${\mathcal L}(\gamma _1)={\mathcal L}(\gamma _2)$
and one of the conditions (i) or (ii) of Theorem 1.43 holds. Indeed, if
${\mathcal L}(\gamma _1)={\mathcal L}(\gamma _2)$
and one of the conditions (i) or (ii) of Theorem 1.43 holds. Indeed, if
![]() $\Phi $
is a symplectomorphism commuting with
$\Phi $
is a symplectomorphism commuting with
![]() ${\Lambda } $
and smooth on
${\Lambda } $
and smooth on
![]() $V_1\cup \widetilde {J}_1$
, then its restriction to
$V_1\cup \widetilde {J}_1$
, then its restriction to
![]() $\widetilde {J}_1$
should be a translation (Proposition 1.45). This implies that the lengths of the intervals
$\widetilde {J}_1$
should be a translation (Proposition 1.45). This implies that the lengths of the intervals
![]() $\widetilde {J}_1$
and
$\widetilde {J}_1$
and
![]() $\widetilde {J}_2=\Phi (\widetilde {J}_1)$
are equal (that is, the Lazutkin lengths of the curves
$\widetilde {J}_2=\Phi (\widetilde {J}_1)$
are equal (that is, the Lazutkin lengths of the curves
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\gamma _2$
are equal) and at least one of the conditions (i) or (ii) holds. Conversely, if
$\gamma _2$
are equal) and at least one of the conditions (i) or (ii) holds. Conversely, if
![]() ${\mathcal L}(\gamma _1)={\mathcal L}(\gamma _2)$
and one of the conditions (i) or (ii) holds, then we can and will consider that
${\mathcal L}(\gamma _1)={\mathcal L}(\gamma _2)$
and one of the conditions (i) or (ii) holds, then we can and will consider that
![]() $\widetilde {J}_1=\widetilde {J}_2$
, applying a translation. Then
$\widetilde {J}_1=\widetilde {J}_2$
, applying a translation. Then
![]() $\Phi =\mathrm {Id}$
has the required properties. This proves Theorem 1.44.
$\Phi =\mathrm {Id}$
has the required properties. This proves Theorem 1.44.
Proof of Theorem 1.43
Let us repeat the above argument, where now the above diffeomorphism
![]() $\Phi :V_1\cup \widetilde {J}_1\to V_2\cup \widetilde {J}_2$
commuting with
$\Phi :V_1\cup \widetilde {J}_1\to V_2\cup \widetilde {J}_2$
commuting with
![]() ${\Lambda } $
is not necessarily symplectic. Let such a
${\Lambda } $
is not necessarily symplectic. Let such a
![]() $\Phi $
exist. Then its restriction to
$\Phi $
exist. Then its restriction to
![]() $\widetilde {J}_1$
is an affine map in the first coordinate,
$\widetilde {J}_1$
is an affine map in the first coordinate,
![]() $t\mapsto \alpha t+\beta $
(Proposition 1.45), and
$t\mapsto \alpha t+\beta $
(Proposition 1.45), and
![]() $\widetilde {J}_2=\Phi (\widetilde {J}_1)$
. This implies that
$\widetilde {J}_2=\Phi (\widetilde {J}_1)$
. This implies that
![]() ${\mathcal L}(\gamma _2)=\alpha {\mathcal L}(\gamma _1)$
, and one of the conditions (i) or (ii) holds. Conversely, let one of the conditions (i) or (ii) hold. Then, without loss of generality, we can and will consider that the interval
${\mathcal L}(\gamma _2)=\alpha {\mathcal L}(\gamma _1)$
, and one of the conditions (i) or (ii) holds. Conversely, let one of the conditions (i) or (ii) hold. Then, without loss of generality, we can and will consider that the interval
![]() $\widetilde {J}_2$
is obtained from
$\widetilde {J}_2$
is obtained from
![]() $\widetilde {J}_1$
by a homothety
$\widetilde {J}_1$
by a homothety
![]() $t\mapsto \alpha t$
, applying a translation. The latter homothety extends to the linear map
$t\mapsto \alpha t$
, applying a translation. The latter homothety extends to the linear map
![]() $\Phi :(t,z)\mapsto (\alpha t,\alpha ^2z)$
commuting with
$\Phi :(t,z)\mapsto (\alpha t,\alpha ^2z)$
commuting with
![]() ${\Lambda } $
and thus having the required properties. The statement of Theorem 1.43 on conjugacy in
${\Lambda } $
and thus having the required properties. The statement of Theorem 1.43 on conjugacy in
![]() $(s,y)$
-coordinates is proved. Together with Remark 1.38, it implies that if one of the conditions (i) or (ii) holds, then the billiard maps are
$(s,y)$
-coordinates is proved. Together with Remark 1.38, it implies that if one of the conditions (i) or (ii) holds, then the billiard maps are
![]() $C^\infty $
-smoothly conjugated near the boundary in
$C^\infty $
-smoothly conjugated near the boundary in
![]() $(s,\phi )$
-coordinates. Let us prove the converse:
$(s,\phi )$
-coordinates. Let us prove the converse:
![]() $C^\infty $
-smooth conjugacy in
$C^\infty $
-smooth conjugacy in
![]() $(s,\phi )$
-coordinates implies that one of the conditions (i) or (ii) holds.
$(s,\phi )$
-coordinates implies that one of the conditions (i) or (ii) holds.
Let
![]() $\widetilde {H}$
be a
$\widetilde {H}$
be a
![]() $C^\infty $
-smooth diffeomorphism conjugating the billiard maps
$C^\infty $
-smooth diffeomorphism conjugating the billiard maps
![]() ${\mathcal T}_{\gamma _1}$
and
${\mathcal T}_{\gamma _1}$
and
![]() ${\mathcal T}_{\gamma _2}$
near the boundary in
${\mathcal T}_{\gamma _2}$
near the boundary in
![]() $(s,\phi )$
-coordinates,
$(s,\phi )$
-coordinates,
![]() $\widetilde {H}\circ {\mathcal T}_{\gamma _1}\circ \widetilde {H}^{-1}={\mathcal T}_{\gamma _2}$
. Let
$\widetilde {H}\circ {\mathcal T}_{\gamma _1}\circ \widetilde {H}^{-1}={\mathcal T}_{\gamma _2}$
. Let
![]() $H_i$
be symplectomorphisms conjugating the billiard maps
$H_i$
be symplectomorphisms conjugating the billiard maps
![]() ${\mathcal T}_{\gamma _i}$
in
${\mathcal T}_{\gamma _i}$
in
![]() $(s,y)$
-coordinates with the map
$(s,y)$
-coordinates with the map
![]() ${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
, see the above proof of Theorem 1.44. The variable changes
${\Lambda } :(t,z)\mapsto (t+\sqrt z,z)$
, see the above proof of Theorem 1.44. The variable changes
lift each diffeomorphism
![]() $H_i$
to a diffeomorphism
$H_i$
to a diffeomorphism
![]() $\widehat H_i(s,\phi )=(\widehat H_{1i}(s,\phi ),\widehat H_{2i}(s,\widetilde {\phi }))$
conjugating the corresponding billiard map with the map
$\widehat H_i(s,\phi )=(\widehat H_{1i}(s,\phi ),\widehat H_{2i}(s,\widetilde {\phi }))$
conjugating the corresponding billiard map with the map
![]() $\widetilde {\Lambda } :(t,\widetilde {z})\mapsto (t+\widetilde {z},\widetilde {z})$
. Then the restriction of its first component
$\widetilde {\Lambda } :(t,\widetilde {z})\mapsto (t+\widetilde {z},\widetilde {z})$
. Then the restriction of its first component
![]() $\widehat H_{1i}(s,0)=H_{1i}(s,0)$
to the s-axis coincides with the Lazutkin parameter
$\widehat H_{1i}(s,0)=H_{1i}(s,0)$
to the s-axis coincides with the Lazutkin parameter
![]() $t_L$
of the curve
$t_L$
of the curve
![]() $\gamma _i$
up to post-composition with affine transformation, by Proposition 1.45. Set
$\gamma _i$
up to post-composition with affine transformation, by Proposition 1.45. Set
![]() $\widehat J_i:=H_{1i}(J_{\gamma _i})$
. The diffeomorphism
$\widehat J_i:=H_{1i}(J_{\gamma _i})$
. The diffeomorphism
![]() $\Phi :=\widehat H_2\circ \widetilde {H}\circ \widehat H_1^{-1}$
commutes with
$\Phi :=\widehat H_2\circ \widetilde {H}\circ \widehat H_1^{-1}$
commutes with
![]() $\widetilde {\Lambda } $
, sends the interval
$\widetilde {\Lambda } $
, sends the interval
![]() $\widehat J_1$
onto
$\widehat J_1$
onto
![]() $\widehat J_2$
, and sends a domain in
$\widehat J_2$
, and sends a domain in
![]() ${\mathbb R}\times {\mathbb R}_+$
adjacent to
${\mathbb R}\times {\mathbb R}_+$
adjacent to
![]() $\widehat J_1$
onto a domain in
$\widehat J_1$
onto a domain in
![]() ${\mathbb R}\times {\mathbb R}_+$
adjacent to
${\mathbb R}\times {\mathbb R}_+$
adjacent to
![]() $\widehat J_2$
. Therefore, the restriction of its first component to
$\widehat J_2$
. Therefore, the restriction of its first component to
![]() $\widehat J_1$
is an affine map
$\widehat J_1$
is an affine map
![]() $t\mapsto \alpha t+\beta $
, by Proposition 1.46. Thus,
$t\mapsto \alpha t+\beta $
, by Proposition 1.46. Thus,
![]() $\widehat J_2$
is a rescaled image of the interval
$\widehat J_2$
is a rescaled image of the interval
![]() $\widehat J_1$
up to translation. Recall that the lengths of the intervals
$\widehat J_1$
up to translation. Recall that the lengths of the intervals
![]() $\widehat J_i$
are equal to the Lazutkin lengths of the corresponding curves
$\widehat J_i$
are equal to the Lazutkin lengths of the corresponding curves
![]() $\gamma _i$
divided by
$\gamma _i$
divided by
![]() $2$
, see equation (2.57). This implies that the improper integrals defining the Lazutkin lengths of the curves
$2$
, see equation (2.57). This implies that the improper integrals defining the Lazutkin lengths of the curves
![]() $\gamma _i$
converge or diverge simultaneously, and one of the conditions (i) or (ii) holds. Theorem 1.43 is proved.
$\gamma _i$
converge or diverge simultaneously, and one of the conditions (i) or (ii) holds. Theorem 1.43 is proved.
Proof of Lemma 1.47
Consider a strictly convex
![]() $C^2$
-smooth planar curve
$C^2$
-smooth planar curve
![]() $\gamma $
going to infinity that has an asymptotic tangent line at infinity. Without loss of generality, we can and will consider that the latter tangent line is the horizontal x-axis in
$\gamma $
going to infinity that has an asymptotic tangent line at infinity. Without loss of generality, we can and will consider that the latter tangent line is the horizontal x-axis in
![]() ${\mathbb R}^2_{x,y}$
,
${\mathbb R}^2_{x,y}$
,
![]() $\gamma $
lies above it, and
$\gamma $
lies above it, and
![]() $\gamma $
is the graph of a
$\gamma $
is the graph of a
![]() $C^2$
-smooth function f defined on
$C^2$
-smooth function f defined on
![]() $[1,+\infty )$
,
$[1,+\infty )$
,
![]() $\gamma =\{ y=f(x)\}$
,
$\gamma =\{ y=f(x)\}$
,
One can achieve this by applying rotation sending the asymptotic line to the x-axis, restricting ourselves to a subarc of the curve
![]() $\gamma $
with the same asymptotic line and applying symmetry with respect to the x-axis, if necessary. The improper integral defining the Lazutkin length of the curve
$\gamma $
with the same asymptotic line and applying symmetry with respect to the x-axis, if necessary. The improper integral defining the Lazutkin length of the curve
![]() $\gamma $
takes the form
$\gamma $
takes the form
 $$ \begin{align} \int_1^{+\infty}\kappa^{2/3}(s)\,ds, \quad \kappa(s(x))=\frac{f"(x)}{(1+(f'(x))^2)^{3/2}},\quad ds=\sqrt{1+(f'(x))^2}\,dx. \end{align} $$
$$ \begin{align} \int_1^{+\infty}\kappa^{2/3}(s)\,ds, \quad \kappa(s(x))=\frac{f"(x)}{(1+(f'(x))^2)^{3/2}},\quad ds=\sqrt{1+(f'(x))^2}\,dx. \end{align} $$
Its convergence is equivalent to the convergence of the integral
 $$ \begin{align} \int_1^{+\infty}(f"(x))^{2/3}\,dx, \end{align} $$
$$ \begin{align} \int_1^{+\infty}(f"(x))^{2/3}\,dx, \end{align} $$
since
![]() $f'(x)\to 0$
, thus,
$f'(x)\to 0$
, thus,
![]() $1+(f'(x))^2\to 1$
, as
$1+(f'(x))^2\to 1$
, as
![]() $x\to + \infty $
.
$x\to + \infty $
.
Claim 8. For every
![]() $C^2$
-smooth function f as in equation (2.58), the improper integral in equation (2.60) converges.
$C^2$
-smooth function f as in equation (2.58), the improper integral in equation (2.60) converges.
Proof. The integral in equation (2.60) is estimated from above by Hölder inequality:
 $$ \begin{align} \int_1^{+\infty}(f"(x))^{2/3}\,dx &=\int_1^{+\infty}(xf"(x))^{2/3}x^{-(2/3)}\,dx \notag \\ &\leq\bigg(\int_1^{+\infty}xf"(x)\,dx\bigg)^{2/3} \bigg(\int_1^{+\infty}\frac{dx}{x^2}\bigg)^{1/3}. \end{align} $$
$$ \begin{align} \int_1^{+\infty}(f"(x))^{2/3}\,dx &=\int_1^{+\infty}(xf"(x))^{2/3}x^{-(2/3)}\,dx \notag \\ &\leq\bigg(\int_1^{+\infty}xf"(x)\,dx\bigg)^{2/3} \bigg(\int_1^{+\infty}\frac{dx}{x^2}\bigg)^{1/3}. \end{align} $$
Therefore, it remains to prove that the integral
![]() $\int _1^{+\infty }xf"(x)\,dx$
converges. Integrating by parts yields
$\int _1^{+\infty }xf"(x)\,dx$
converges. Integrating by parts yields
 $$ \begin{align} \int_1^{+\infty}xf"(x)\,dx=xf'(x)|_1^{+\infty}-\int_1^{+\infty}f'(x)\,dx=xf'(x)|_1^{+\infty}-f(1). \end{align} $$
$$ \begin{align} \int_1^{+\infty}xf"(x)\,dx=xf'(x)|_1^{+\infty}-\int_1^{+\infty}f'(x)\,dx=xf'(x)|_1^{+\infty}-f(1). \end{align} $$
Suppose the contrary: the integral on the left-hand side diverges. Then it is equal to
![]() $+\infty $
, since
$+\infty $
, since
![]() $f"(x)>0$
. Therefore,
$f"(x)>0$
. Therefore,
![]() $xf'(x)\to +\infty $
, as
$xf'(x)\to +\infty $
, as
![]() $x\to +\infty $
. Hence,
$x\to +\infty $
. Hence,
![]() $f'(x)> (1/x)$
, whenever x is greater than some constant
$f'(x)> (1/x)$
, whenever x is greater than some constant
![]() $N>1$
. Integrating the latter inequality along the semi-interval
$N>1$
. Integrating the latter inequality along the semi-interval
![]() $[N,+\infty )$
yields
$[N,+\infty )$
yields
![]() $f(N)=+\infty $
. The contradiction thus obtained proves convergence of the integral on the left-hand side in equation (2.62), and hence, of the integral in equation (2.60). The claim is proved.
$f(N)=+\infty $
. The contradiction thus obtained proves convergence of the integral on the left-hand side in equation (2.62), and hence, of the integral in equation (2.60). The claim is proved.
The claim together with equation (2.59) imply convergence of the improper integral defining the Lazutkin length. This proves Lemma 1.47.
Proof of Theorem 1.39
The Lazutkin lengths of both curves
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
are finite, since they have asymptotic tangent lines at infinity in both directions and by Lemma 1.47. This together with Theorem 1.43 implies
$\gamma _2$
are finite, since they have asymptotic tangent lines at infinity in both directions and by Lemma 1.47. This together with Theorem 1.43 implies
![]() $C^\infty $
-smooth conjugacy of the corresponding billiard maps near the boundary and up to the boundary. Theorem 1.39 is proved.
$C^\infty $
-smooth conjugacy of the corresponding billiard maps near the boundary and up to the boundary. Theorem 1.39 is proved.
The proof of Theorem 1.40 is analogous to the above proof of Theorem 1.39.
Acknowledgements
I am grateful to Marie-Claude Arnaud, Sergei Tabachnikov, Alexander Plakhov, Ivan Beschastnyi, Stefano Baranzini, Vadim Kaloshin, and Comlan Koudjinan for helpful discussions. I am grateful to the referees for careful reading the paper and for very helpful remarks. This work was partly supported by the Laboratory of Dynamical Systems and Applications, HSE University, of the Ministry of Science and Higher Education of RF, grant agreement No 075-15-2019-1931 and by RFBR according to the research project 20-01-00420.