No CrossRef data available.
Article contents
On infinitely cohomologous to zero observables
Published online by Cambridge University Press: 08 February 2012
Abstract
We show that for a large class of piecewise expanding maps T, the bounded p-variation observables u0 that admit an infinite sequence of bounded p-variation observables ui satisfying are constant. The method of the proof consists of finding a suitable Hilbert basis for L2(hm), where hm is the unique absolutely continuous invariant probability of T. On this basis, the action of the Perron–Frobenius and the Koopman operator on L2(hm)can be easily understood. This result generalizes earlier results by Bamón, Kiwi, Rivera-Letelier and Urzúa for the case T(x)=ℓx mod 1 , ℓ∈ℕ∖ {0,1} and Lipschitzian observables u0.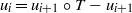
\[ u_{i}= u_{i+1}\circ T-u_{i+1} \]
Information
- Type
- Research Article
- Information
- Copyright
- ©2012 Cambridge University Press
References
[1]de Lima, A.. Cohomologia e propriedades estocásticas de transformações expansoras e observáveis lipschitzianos. Master’s Thesis, ICMC-USP, 2007.Google Scholar
[3]Baladi, V.. Positive Transfer Operators and Decay of Correlations (Advanced Series in Nonlinear Dynamics, 16). World Scientific, Singapore, 2000.Google Scholar
[4]Bamón, R., Rivera-Letelier, J., Kiwi, J. and Urzúa, R.. On the topology of solenoidal attractors of the cylinder. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(2) (2006), 209–236.Google Scholar
[5]Broise, A.. Transformations Dilatantes de L’Intervalle et Théorème Limites. Études Spectrales D’Opérateurs de Transfert et Applications (Asterisque, 238). 1996.Google Scholar
[6]Goffman, C., Nishiura, T. and Waterman, D.. Homeomorphisms in Analysis (Mathematical Surveys and Monographs, 54). American Mathematical Society, 1997.Google Scholar
[7]Pollicott, M.. Meromorphic extensions of generalised zeta functions. Invent. Math. 85(1) (1986), 147–164.Google Scholar
[8]Shub, M. and Sullivan, D.. Expanding endomorphisms of the circle revisited. Ergod. Th. & Dynam. Sys. 5 (1985), 285–289.Google Scholar
[9]Viana, M.. Stochastic dynamics of deterministic systems. Colóquio Brasileiro de Matemática-IMPA (1997).Google Scholar
[10]Wong, S.. Holder continuous derivatives and ergodic theory. J. Lond. Math. Soc. s2-22(3) (1980), 506–520.Google Scholar