Article contents
On an extension of Mycielski’s theorem and invariant scrambled sets
Published online by Cambridge University Press: 10 November 2014
Abstract
Let  $(X,f)$ be a dynamical system, where
$(X,f)$ be a dynamical system, where 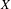 $X$ is a perfect Polish space and
$X$ is a perfect Polish space and 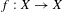 $f:X\rightarrow X$ is a continuous map. In this paper we study the invariant dependent sets of a given relation string
$f:X\rightarrow X$ is a continuous map. In this paper we study the invariant dependent sets of a given relation string 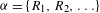 ${\it\alpha}=\{R_{1},R_{2},\ldots \}$ on
${\it\alpha}=\{R_{1},R_{2},\ldots \}$ on 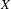 $X$. To do so, we need the relation string
$X$. To do so, we need the relation string  ${\it\alpha}$ to satisfy some dynamical properties, and we say that
${\it\alpha}$ to satisfy some dynamical properties, and we say that  ${\it\alpha}$ is
${\it\alpha}$ is 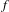 $f$-invariant (see Definition 3.1). We show that if
$f$-invariant (see Definition 3.1). We show that if 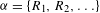 ${\it\alpha}=\{R_{1},R_{2},\ldots \}$ is an
${\it\alpha}=\{R_{1},R_{2},\ldots \}$ is an  $f$-invariant relation string and
$f$-invariant relation string and 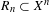 $R_{n}\subset X^{n}$ is a residual subset for each
$R_{n}\subset X^{n}$ is a residual subset for each 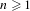 $n\geq 1$, then there exists a dense Mycielski subset
$n\geq 1$, then there exists a dense Mycielski subset 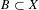 $B\subset X$ such that the invariant subset
$B\subset X$ such that the invariant subset 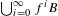 $\bigcup _{i=0}^{\infty }f^{i}B$ is a dependent set of
$\bigcup _{i=0}^{\infty }f^{i}B$ is a dependent set of 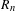 $R_{n}$ for each
$R_{n}$ for each 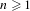 $n\geq 1$ (see Theorems 5.4 and 5.5). This result extends Mycielski’s theorem (see Theorem A) when
$n\geq 1$ (see Theorems 5.4 and 5.5). This result extends Mycielski’s theorem (see Theorem A) when 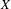 $X$ is a perfect Polish space (see Corollary 5.6). Furthermore, in two applications of the main results, we simplify the proofs of known results on chaotic sets in an elegant way.
$X$ is a perfect Polish space (see Corollary 5.6). Furthermore, in two applications of the main results, we simplify the proofs of known results on chaotic sets in an elegant way.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 4
- Cited by

