Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-27T13:33:39.563Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-constant invariant function for certain ergodic flows

Published online by Cambridge University Press:  01 June 2008

SOL SCHWARTZMAN
SOL SCHWARTZMAN*
Affiliation:
Department of Mathematics, University of Rhode Island, Kingston, RI 02906, USA (email: schwartzman@math.uri.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let U be the vector space of uniformly continuous real-valued functions on the real line 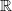and let U0 denote the subspace of U consisting of all bounded uniformly continuous functions. If X is a compact differentiable manifold and we are given a flow on X, then we associate with the flow a function F:X→H1(X,U/U0) that is invariant under the flow. We give examples for which the flow on X is ergodic but there is no λ∈H1(X,U/U0) such that F(p)=λ for almost all points p.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 1031 - 1035
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Katok, S.. Fuchsian groups. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, 1992.Google Scholar
[2]Schwartzman, S.. Asymptotic cycles. Ann. of Math. 66(2) (1957), 270–284.CrossRefGoogle Scholar
[3]Schwartzman, S.. Uniform and Lipschitz homotopy classes of maps. Trans. Amer. Math. Soc. 354(12) (2002), 5039–5047.CrossRefGoogle Scholar