Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gutman, Yonatan
2015.
Mean dimension and Jaworski-type theorems.
Proceedings of the London Mathematical Society,
Vol. 111,
Issue. 4,
p.
831.
Gutman, Yonatan
Lindenstrauss, Elon
and
Tsukamoto, Masaki
2016.
Mean dimension of $${\mathbb{Z}^k}$$ Z k -actions.
Geometric and Functional Analysis,
Vol. 26,
Issue. 3,
p.
778.
GUTMAN, YONATAN
2017.
Embedding topological dynamical systems with periodic points in cubical shifts.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 2,
p.
512.
Dou, Dou
2017.
Minimal subshifts of arbitrary mean topological dimension.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 3,
p.
1411.
Gutman, Yonatan
Qiao, Yixiao
and
Szabó, Gábor
2018.
The embedding problem in topological dynamics and Takens’ theorem.
Nonlinearity,
Vol. 31,
Issue. 2,
p.
597.
Tsukamoto, Masaki
2018.
Large dynamics of Yang–Mills theory: mean dimension formula.
Journal d'Analyse Mathématique,
Vol. 134,
Issue. 2,
p.
455.
MA, XIANFENG
YANG, JUNQI
and
CHEN, ERCAI
2019.
Mean topological dimension for random bundle transformations.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 4,
p.
1020.
Li, Hanfeng
and
Liang, Bingbing
2019.
Sofic mean length.
Advances in Mathematics,
Vol. 353,
Issue. ,
p.
802.
Tang, Dingxuan
Wu, Haiyan
and
Li, Zhiming
2020.
Weighted upper metric mean dimension for amenable group actions.
Dynamical Systems,
Vol. 35,
Issue. 3,
p.
382.
Gutman, Yonatan
and
Tsukamoto, Masaki
2020.
Embedding minimal dynamical systems into Hilbert cubes.
Inventiones mathematicae,
Vol. 221,
Issue. 1,
p.
113.
Li, Zhiming
2021.
Amenable upper mean dimensions.
Analysis and Mathematical Physics,
Vol. 11,
Issue. 3,
LIANG, BINGBING
2021.
Conditional mean dimension.
Ergodic Theory and Dynamical Systems,
p.
1.
Chen, Ercai
Dou, Dou
and
Zheng, Dongmei
2022.
Variational principles for amenable metric mean dimensions.
Journal of Differential Equations,
Vol. 319,
Issue. ,
p.
41.
Kato, Hisao
2023.
Takens-type reconstruction theorems of one-sided dynamical systems.
Nonlinearity,
Vol. 36,
Issue. 3,
p.
1571.
Niu, Zhuang
2024.
Radius of comparison and mean topological dimension: -actions.
Canadian Journal of Mathematics,
Vol. 76,
Issue. 4,
p.
1240.
Kato, Hisao
2025.
Addendum: Takens-type reconstruction theorems of one-sided dynamical systems (2023 Nonlinearity 36 1571).
Nonlinearity,
Vol. 38,
Issue. 7,
p.
079401.
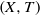 $(X, T)$ is an extension of an aperiodic subshift (a subsystem of
$(X, T)$ is an extension of an aperiodic subshift (a subsystem of 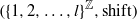 $(\mathop{\{ 1, 2, \ldots , l\} }\nolimits ^{ \mathbb{Z} } , \mathrm{shift} )$ for some
$(\mathop{\{ 1, 2, \ldots , l\} }\nolimits ^{ \mathbb{Z} } , \mathrm{shift} )$ for some 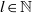 $l\in \mathbb{N} $) and has mean dimension
$l\in \mathbb{N} $) and has mean dimension 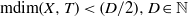 $\mathrm{mdim} (X, T)\lt (D/ 2), D\in \mathbb{N} $, then it can be equivariantly embedded in
$\mathrm{mdim} (X, T)\lt (D/ 2), D\in \mathbb{N} $, then it can be equivariantly embedded in 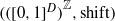 $(\mathop{(\mathop{[0, 1] }\nolimits ^{D} )}\nolimits ^{ \mathbb{Z} } , \mathrm{shift} )$. The result is sharp. If
$(\mathop{(\mathop{[0, 1] }\nolimits ^{D} )}\nolimits ^{ \mathbb{Z} } , \mathrm{shift} )$. The result is sharp. If 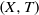 $(X, T)$ is an extension of an aperiodic zero-dimensional system then it can be equivariantly embedded in
$(X, T)$ is an extension of an aperiodic zero-dimensional system then it can be equivariantly embedded in 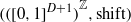 $(\mathop{(\mathop{[0, 1] }\nolimits ^{D+ 1} )}\nolimits ^{ \mathbb{Z} } , \mathrm{shift} )$.
$(\mathop{(\mathop{[0, 1] }\nolimits ^{D+ 1} )}\nolimits ^{ \mathbb{Z} } , \mathrm{shift} )$.