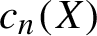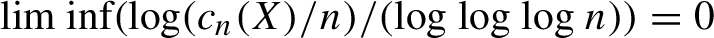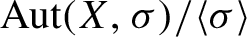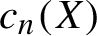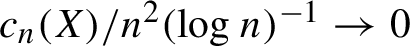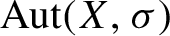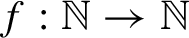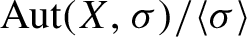1 Introduction
This work deals with symbolic dynamics, which is the study of symbolically defined topological dynamical systems called subshifts. A subshift is simply a closed and shift-invariant subset of
![]() $\mathcal {A}^{\mathbb {Z}}$
for some finite set
$\mathcal {A}^{\mathbb {Z}}$
for some finite set
![]() $\mathcal {A}$
. One way of measuring the size of a subshift X is via its word complexity function
$\mathcal {A}$
. One way of measuring the size of a subshift X is via its word complexity function
![]() $c_n(X)$
;
$c_n(X)$
;
![]() $c_n(X)$
is the number of different n-letter strings (or words) appearing within points of X.
$c_n(X)$
is the number of different n-letter strings (or words) appearing within points of X.
Another sense of ‘complexity’ for a subshift comes from its group of automorphisms; an automorphism of a subshift X is a homeomorphism from X to itself which commutes with the shift map
![]() $\sigma : X \rightarrow X$
defined by
$\sigma : X \rightarrow X$
defined by
![]() $(\sigma x)(n) = x(n+1)$
. The set of automorphisms
$(\sigma x)(n) = x(n+1)$
. The set of automorphisms
![]() $\mathrm {Aut}(X,\sigma )$
has an obvious group structure from composition, and turns out to always be countable. By definition,
$\mathrm {Aut}(X,\sigma )$
has an obvious group structure from composition, and turns out to always be countable. By definition,
![]() $\sigma $
itself is always in
$\sigma $
itself is always in
![]() $\mathrm {Aut}(X,\sigma )$
, and
$\mathrm {Aut}(X,\sigma )$
, and
![]() $\langle \sigma \rangle $
, the subgroup generated by
$\langle \sigma \rangle $
, the subgroup generated by
![]() $\sigma $
, is always a normal subgroup of
$\sigma $
, is always a normal subgroup of
![]() $\mathrm {Aut}(X,\sigma )$
. (See §2 for more details.)
$\mathrm {Aut}(X,\sigma )$
. (See §2 for more details.)
In this paper, we continue a line of research which has been fruitfully developed in many recent works [Reference Cyr and Kra3–Reference Donoso, Durand, Maass and Petite8, Reference Salo16, Reference Salo17], namely: in what sense must subshifts with low complexity functions have automorphism groups which are ‘small’ or restricted? Though we do not claim it to be complete, we summarize some recent results in this area. Some of the following results include the hypothesis of transitivity/minimality of X; we postpone definitions to §2.1.
-
(1) X minimal and
 $\liminf ({c_n(X)}/{n}) < \infty \Longrightarrow {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
finite [Reference Cyr and Kra3, Reference Donoso, Durand, Maass and Petite7].
$\liminf ({c_n(X)}/{n}) < \infty \Longrightarrow {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
finite [Reference Cyr and Kra3, Reference Donoso, Durand, Maass and Petite7]. -
(2) X transitive and
 $\limsup ({c_n(X)}/{n}) < \infty \Longrightarrow {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
finite [Reference Cyr and Kra3].
$\limsup ({c_n(X)}/{n}) < \infty \Longrightarrow {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
finite [Reference Cyr and Kra3]. -
(3)
 $\limsup ({c_n(X)}/{n}) < \infty \Longrightarrow $
all f.g. subgroups of
$\limsup ({c_n(X)}/{n}) < \infty \Longrightarrow $
all f.g. subgroups of
 $\mathrm {Aut}(X,\sigma )$
are virtually
$\mathrm {Aut}(X,\sigma )$
are virtually
 $\mathbb {Z}^d$
[Reference Cyr and Kra3].
$\mathbb {Z}^d$
[Reference Cyr and Kra3]. -
(4)
 ${c_n(X)}/{n^2 (\log n)^{-2}} \rightarrow 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
amenable [Reference Cyr and Kra6].
${c_n(X)}/{n^2 (\log n)^{-2}} \rightarrow 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
amenable [Reference Cyr and Kra6]. -
(5) X transitive and
 $\liminf ({c_n(X)}/{n^2}) = 0 \Longrightarrow {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
periodic [Reference Cyr and Kra5].
$\liminf ({c_n(X)}/{n^2}) = 0 \Longrightarrow {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
periodic [Reference Cyr and Kra5]. -
(6)
 $\liminf ({c_n(X)}/{n^2}) = 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
does not contain a free semigroup on two generators [Reference Cyr and Kra6].
$\liminf ({c_n(X)}/{n^2}) = 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
does not contain a free semigroup on two generators [Reference Cyr and Kra6]. -
(7) X minimal and
 ${c_n(X)}/{n^3} \rightarrow 0 \Longrightarrow $
every f.g. torsion-free subgroup of
${c_n(X)}/{n^3} \rightarrow 0 \Longrightarrow $
every f.g. torsion-free subgroup of
 $\mathrm {Aut}(X,\sigma )$
is virtually abelian [Reference Cyr and Kra4].
$\mathrm {Aut}(X,\sigma )$
is virtually abelian [Reference Cyr and Kra4]. -
(8) X minimal and there exists
 $d \in \mathbb {N}$
with
$d \in \mathbb {N}$
with
 ${c_n(X)}/{n^d} \rightarrow 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
amenable and every f.g. torsion-free subgroup of
${c_n(X)}/{n^d} \rightarrow 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
amenable and every f.g. torsion-free subgroup of
 $\mathrm {Aut}(X,\sigma )$
is virtually nilpotent [Reference Cyr and Kra4].
$\mathrm {Aut}(X,\sigma )$
is virtually nilpotent [Reference Cyr and Kra4]. -
(9) X minimal and there exists
 $\beta < 1/2$
with
$\beta < 1/2$
with
 ${\log c_n(X)}/{n^{\beta }} \rightarrow 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
amenable [Reference Cyr and Kra4].
${\log c_n(X)}/{n^{\beta }} \rightarrow 0 \Longrightarrow \mathrm {Aut}(X,\sigma )$
amenable [Reference Cyr and Kra4].
Here, we wish to add some more context to the transition from linear to slightly greater complexity function; to our knowledge, up to now, there have been no complexity thresholds used between the linear one for items (1)–(3) above and
![]() $o(n^2/\log ^2 n)$
from item (4). It is reasonable to expect that complexity extremely close to linear should place restrictions on the group structure of
$o(n^2/\log ^2 n)$
from item (4). It is reasonable to expect that complexity extremely close to linear should place restrictions on the group structure of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
which are stronger than periodicity. Our first main result shows that for transitive subshifts, low enough complexity in fact implies that
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
which are stronger than periodicity. Our first main result shows that for transitive subshifts, low enough complexity in fact implies that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
Theorem 1.1. If X is an infinite transitive subshift with
![]() $\liminf ({\log (c_n(X)/n)}/ ({\log \log \log n})) = 0$
, then
$\liminf ({\log (c_n(X)/n)}/ ({\log \log \log n})) = 0$
, then
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite (and countable).
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite (and countable).
We briefly remark that local finiteness is a strictly stronger property than periodicity (for instance, the Tarski monster groups and Grigorchuk group are periodic but not locally finite), and so this result has a strictly stronger complexity hypothesis and conclusion than item (5) above.
To prove Theorem 1.1, we first achieve some estimates on growth of number of automorphisms as a function of range by using left- and right-special words (Corollary 3.1). We then use a theorem of Shalom and Tao (Theorem 2.26) to show that our growth is so slow as to force finitely generated subgroups of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
to be virtually nilpotent. Finally, we combine this with the fact that
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
to be virtually nilpotent. Finally, we combine this with the fact that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is known to be periodic under the hypotheses of Theorem 1.1 due to item (5) above; thus all finitely generated subgroups of
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is known to be periodic under the hypotheses of Theorem 1.1 due to item (5) above; thus all finitely generated subgroups of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
are virtually nilpotent and periodic, therefore finite.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
are virtually nilpotent and periodic, therefore finite.
There is a well-known conjecture in geometric group theory called the gap conjecture (see [Reference Grigorchuk9]), which states that every finitely generated group with growth rate
![]() $e^{o(\sqrt {n})}$
(see §2.3 for more details) has polynomial growth. The gap conjecture is known to hold for some classes of groups [Reference Grigorchuk9, Reference Grigorchuk10, Reference Wilson19, Reference Wilson20], but is still open in general.
$e^{o(\sqrt {n})}$
(see §2.3 for more details) has polynomial growth. The gap conjecture is known to hold for some classes of groups [Reference Grigorchuk9, Reference Grigorchuk10, Reference Wilson19, Reference Wilson20], but is still open in general.
Variants of our first main result show that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite under much weaker hypotheses if the gap conjecture is true.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite under much weaker hypotheses if the gap conjecture is true.
Theorem 1.2. If X is a transitive subshift with
![]() $\liminf ({c_n(X)}/{n^{1.25} (\log n)^{-0.5}}) = 0$
and the gap conjecture is true, then
$\liminf ({c_n(X)}/{n^{1.25} (\log n)^{-0.5}}) = 0$
and the gap conjecture is true, then
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite (and countable).
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite (and countable).
Theorem 1.3. If X is a transitive subshift with
![]() ${c_n(X)}/{n^{1.5} (\log n)^{-1}} \rightarrow 0$
and the gap conjecture is true, then
${c_n(X)}/{n^{1.5} (\log n)^{-1}} \rightarrow 0$
and the gap conjecture is true, then
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite (and countable).
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite (and countable).
Finally, our techniques allow for a slight improvement to the theorem of Cyr and Kra referenced as item (4) above, where they proved that if
![]() $(X,\sigma )$
is any subshift satisfying
$(X,\sigma )$
is any subshift satisfying
![]() $c_n(X) = o(n^2/(\log ^2 n))$
, then
$c_n(X) = o(n^2/(\log ^2 n))$
, then
![]() $\mathrm {Aut}(X,\sigma )$
is amenable.
$\mathrm {Aut}(X,\sigma )$
is amenable.
Theorem 1.4. If X is a subshift with
![]() ${c_n(X)}/{n^2 (\log n)^{-1}} \rightarrow 0$
, then
${c_n(X)}/{n^2 (\log n)^{-1}} \rightarrow 0$
, then
![]() $\mathrm {Aut}(X,\sigma )$
is amenable (and countable).
$\mathrm {Aut}(X,\sigma )$
is amenable (and countable).
Our final result is in the opposite direction, showing that no superlinear complexity threshold can impose stronger restrictions on
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
than being locally finite (and countable).
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
than being locally finite (and countable).
Theorem 1.5. For any countable locally finite group G and any unbounded increasing
![]() $f: \mathbb {N} \rightarrow \mathbb {R}$
, there exists a minimal subshift X with
$f: \mathbb {N} \rightarrow \mathbb {R}$
, there exists a minimal subshift X with
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }} = G$
and
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }} = G$
and
![]() ${c_n(X)}/{nf(n)} \rightarrow ~0$
.
${c_n(X)}/{nf(n)} \rightarrow ~0$
.
In particular, Theorem 1.5 provides examples of minimal subshifts having arbitrarily slow but superlinear complexity function whose automorphism group is not virtually abelian, demonstrating that the words ‘finitely generated torsion-free’ cannot be omitted in item (7) above. For example, if one applies Theorem 1.5 in the case where G is a countably infinite locally finite simple group, then in this case,
![]() $\mathrm {Aut}(X,\sigma )$
can not be virtually abelian.
$\mathrm {Aut}(X,\sigma )$
can not be virtually abelian.
Remark 1.6. Theorems 1.1 and 1.5 together completely characterize the possible
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
for transitive subshifts X with growth
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
for transitive subshifts X with growth
![]() $n (\log \log n)^{o(1)}$
along a subsequence: they are exactly the locally finite groups.
$n (\log \log n)^{o(1)}$
along a subsequence: they are exactly the locally finite groups.
Remark 1.7. We would like to mention [Reference Bernales and Donoso1], where they prove several results similar in spirit to Theorem 1.5, one of which realizes arbitrary Choquet simplices of invariant measures for (minimal) Toeplitz subshifts of arbitrarily low superlinear complexity. In addition to providing a class of examples satisfying our complexity assumptions in Theorems 1.1–1.4, this also shows that there are subshifts with arbitrary (for instance very large) Choquet simplices and
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
locally finite.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
locally finite.
2 Definitions/preliminaries
2.1 Symbolic dynamics
Definition 2.1. For any finite alphabet
![]() $\mathcal {A}$
, the full shift over
$\mathcal {A}$
, the full shift over
![]() $\mathcal {A}$
is the set
$\mathcal {A}$
is the set
![]() $\mathcal {A}^{\mathbb {Z}}$
, which is viewed as a compact topological space with the (discrete) product topology.
$\mathcal {A}^{\mathbb {Z}}$
, which is viewed as a compact topological space with the (discrete) product topology.
Definition 2.2. A word over
![]() $\mathcal {A}$
is an element
$\mathcal {A}$
is an element
![]() $w \in \mathcal {A}^n$
for some
$w \in \mathcal {A}^n$
for some
![]() $n \in \mathbb {N}$
, which is referred to as its length and denoted by
$n \in \mathbb {N}$
, which is referred to as its length and denoted by
![]() $|w|$
. We say that a word v is a subword of a word or biinfinite sequence x if there exists i so that
$|w|$
. We say that a word v is a subword of a word or biinfinite sequence x if there exists i so that
![]() $x([i, i+|w|)) = w$
. (Here and throughout, all intervals are assumed to be intersected with
$x([i, i+|w|)) = w$
. (Here and throughout, all intervals are assumed to be intersected with
![]() $\mathbb {Z}$
, e.g.
$\mathbb {Z}$
, e.g.
![]() $[2,5)$
represents
$[2,5)$
represents
![]() $\{2,3,4\}$
. For such an interval I, we view an element of
$\{2,3,4\}$
. For such an interval I, we view an element of
![]() $\mathcal {A}^I$
as a word of length
$\mathcal {A}^I$
as a word of length
![]() $|I|$
by the obvious identification.)
$|I|$
by the obvious identification.)
The set of words has an obvious binary operation of concatenation, and whenever we write expressions like
![]() $vw$
or
$vw$
or
![]() $w^3$
, it is with respect to concatenation.
$w^3$
, it is with respect to concatenation.
Definition 2.3. The left shift, denoted by
![]() $\sigma $
, is the self-map of the full shift defined by
$\sigma $
, is the self-map of the full shift defined by
![]() $(\sigma x)(n) = x(n+1)$
for
$(\sigma x)(n) = x(n+1)$
for
![]() $x \in \mathcal {A}^{\mathbb {Z}}$
and
$x \in \mathcal {A}^{\mathbb {Z}}$
and
![]() $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
Definition 2.4. A subshift over
![]() $\mathcal {A}$
is a topological dynamical system
$\mathcal {A}$
is a topological dynamical system
![]() $(X, \sigma )$
, where X is a closed subset of the full shift
$(X, \sigma )$
, where X is a closed subset of the full shift
![]() $\mathcal {A}^{\mathbb {Z}^d}$
(endowed with the subspace (product) topology) which is invariant under
$\mathcal {A}^{\mathbb {Z}^d}$
(endowed with the subspace (product) topology) which is invariant under
![]() $\sigma $
.
$\sigma $
.
Since there is never ambiguity about the dynamics on X, in this work, we refer to a subshift simply by the space X for ease of notation.
Definition 2.5. A word, one-sided infinite sequence, or bi-infinite sequence x over
![]() $\mathcal {A}$
is periodic with period p if
$\mathcal {A}$
is periodic with period p if
![]() $x(n) = x(n+p)$
for all
$x(n) = x(n+p)$
for all
![]() $n \in \mathbb {Z}$
, where both
$n \in \mathbb {Z}$
, where both
![]() $x(n)$
and
$x(n)$
and
![]() $x(n+p)$
are defined.
$x(n+p)$
are defined.
Definition 2.6. The language of a subshift X, denoted by
![]() $L(X)$
, is the set of all subwords of sequences in X. For all n, we write
$L(X)$
, is the set of all subwords of sequences in X. For all n, we write
![]() $L_n(X) = L(X) \cap \mathcal {A}^n$
for the set of words of length n in
$L_n(X) = L(X) \cap \mathcal {A}^n$
for the set of words of length n in
![]() $L(X)$
.
$L(X)$
.
Definition 2.7. A word w is right-special for a subshift X if there exist
![]() $a \neq b \in \mathcal {A}$
for which
$a \neq b \in \mathcal {A}$
for which
![]() $wa, wb \in L(X)$
. Similarly, w is left-special for X if there exist
$wa, wb \in L(X)$
. Similarly, w is left-special for X if there exist
![]() $c \neq d \in \mathcal {A}$
for which
$c \neq d \in \mathcal {A}$
for which
![]() $cw, dw \in L(X)$
. The sets of n-letter right-special and left-special words for X are denoted by
$cw, dw \in L(X)$
. The sets of n-letter right-special and left-special words for X are denoted by
![]() $RS_n(X)$
and
$RS_n(X)$
and
![]() $LS_n(X)$
respectively.
$LS_n(X)$
respectively.
Definition 2.8. The word complexity sequence of a subshift X is defined by
![]() $c_n(X) := |L_n(X)|$
.
$c_n(X) := |L_n(X)|$
.
The following lemma is routine, but we include a proof for completeness.
Lemma 2.9. For any subshift X and
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $|LS_n(X)|$
and
$|LS_n(X)|$
and
![]() $|RS_n(X)|$
are less than or equal to
$|RS_n(X)|$
are less than or equal to
![]() $c_{n+1}(X) - c_n(X)$
.
$c_{n+1}(X) - c_n(X)$
.
Proof. We give only the proof for
![]() $|RS_n(X)|$
, as the other is trivially similar. Fix any X and n, and consider the map
$|RS_n(X)|$
, as the other is trivially similar. Fix any X and n, and consider the map
![]() $f: L_{n+1}(X) \rightarrow L_n(X)$
removing the final letter of an
$f: L_{n+1}(X) \rightarrow L_n(X)$
removing the final letter of an
![]() $n+1$
-letter word. This map is surjective, and it is clear from definition that
$n+1$
-letter word. This map is surjective, and it is clear from definition that
![]() $w \in L_n(X)$
is right-special if and only if its f-preimage has cardinality greater than
$w \in L_n(X)$
is right-special if and only if its f-preimage has cardinality greater than
![]() $1$
. From this, it is immediate that
$1$
. From this, it is immediate that
![]() $|RS_n(X)| \leq c_{n+1}(X) - c_n(X)$
.
$|RS_n(X)| \leq c_{n+1}(X) - c_n(X)$
.
Definition 2.10. A subshift X is minimal if for all
![]() $w \in L(X)$
and
$w \in L(X)$
and
![]() $x \in X$
, w is a subword of x.
$x \in X$
, w is a subword of x.
Definition 2.11. A subshift X is (topologically) transitive if there exists
![]() $x \in X$
so that
$x \in X$
so that
![]() $X = \overline {\{\sigma ^n x \ : \ n \in \mathbb {Z}}\}$
.
$X = \overline {\{\sigma ^n x \ : \ n \in \mathbb {Z}}\}$
.
We briefly note that an infinite transitive subshift X cannot have isolated periodic points; if X is transitive, then there exists
![]() $x \in X$
for which
$x \in X$
for which
![]() $X = \overline {\{\sigma ^n x \ : \ n \in \mathbb {Z}\}}$
. If
$X = \overline {\{\sigma ^n x \ : \ n \in \mathbb {Z}\}}$
. If
![]() $p \in X$
were isolated and periodic, then
$p \in X$
were isolated and periodic, then
![]() $p \in \{\sigma ^n x\}$
, implying that
$p \in \{\sigma ^n x\}$
, implying that
![]() $X = \{\sigma ^n p\}$
and that X is finite by periodicity of p, a contradiction.
$X = \{\sigma ^n p\}$
and that X is finite by periodicity of p, a contradiction.
Definition 2.12. A (topological) factor map from one subshift X to another subshift
![]() $X'$
is a surjective continuous function
$X'$
is a surjective continuous function
![]() $\phi : X \rightarrow X'$
which commutes with the shift action (that is
$\phi : X \rightarrow X'$
which commutes with the shift action (that is
![]() $\phi \circ \sigma = \sigma \circ \phi $
).
$\phi \circ \sigma = \sigma \circ \phi $
).
By the classical Curtis–Hedlund–Lyndon theorem, factor maps on subshifts have a very specific form.
Theorem 2.13. For any factor map
![]() $\phi : X \rightarrow X'$
, there exists N and
$\phi : X \rightarrow X'$
, there exists N and
 $\Phi : \mathcal {A}_X^{2N+1} \rightarrow \mathcal {A}_{X'}$
so that for all
$\Phi : \mathcal {A}_X^{2N+1} \rightarrow \mathcal {A}_{X'}$
so that for all
![]() $x \in X$
and
$x \in X$
and
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $(\phi x)(n) = \Phi (x([n-N, n+N]))$
.
$(\phi x)(n) = \Phi (x([n-N, n+N]))$
.
Definition 2.14. We say that a factor map
![]() $\phi $
has range N and has inducing block map
$\phi $
has range N and has inducing block map
![]() $\Phi $
if it satisfies the conclusion of Theorem 2.13.
$\Phi $
if it satisfies the conclusion of Theorem 2.13.
We remark that though every factor
![]() $\phi $
has some range N and inducing block map
$\phi $
has some range N and inducing block map
![]() $\Phi $
, these need not be unique.
$\Phi $
, these need not be unique.
Definition 2.15. An automorphism of a subshift X is a factor map from X to itself which is bijective.
If
![]() $\phi $
is an automorphism of X with inducing block map
$\phi $
is an automorphism of X with inducing block map
 $\Phi : \mathcal {A}_X^{2N+1} \rightarrow \mathcal {A}$
, then for every word
$\Phi : \mathcal {A}_X^{2N+1} \rightarrow \mathcal {A}$
, then for every word
![]() $w \in L_n(X)$
with
$w \in L_n(X)$
with
![]() $n \geq 2N+1$
, we can let
$n \geq 2N+1$
, we can let
![]() $\Phi $
act on w as in the definition of
$\Phi $
act on w as in the definition of
![]() $\phi $
. Formally, let
$\phi $
. Formally, let
![]() $\Phi (w)$
be the word of length
$\Phi (w)$
be the word of length
![]() $n - 2N$
defined by
$n - 2N$
defined by
![]() $(\Phi (w))(i) = \Phi (w([i-N, i+N]))$
for
$(\Phi (w))(i) = \Phi (w([i-N, i+N]))$
for
![]() $N < i \leq n - N$
.
$N < i \leq n - N$
.
We remark that ranges of automorphisms are additive under composition. Indeed, by definition, if
![]() $\phi $
has range N and inducing map
$\phi $
has range N and inducing map
![]() $\Phi $
and
$\Phi $
and
![]() $\phi '$
has range
$\phi '$
has range
![]() $N'$
and inducing map
$N'$
and inducing map
![]() $\Phi '$
, then
$\Phi '$
, then
![]() $\phi \circ \phi '$
has range
$\phi \circ \phi '$
has range
![]() $N+N'$
and inducing map
$N+N'$
and inducing map
![]() $\Phi \circ \Phi '$
(where
$\Phi \circ \Phi '$
(where
![]() $\Phi '$
acts on words in
$\Phi '$
acts on words in
 $\mathcal {A}_X^{2N+2N'+1}$
, as defined above.)
$\mathcal {A}_X^{2N+2N'+1}$
, as defined above.)
2.2 Group theory
We here summarize some basic definitions from group theory. We will not have need of any advanced group theory in this paper, so we do not go into great detail. For more information, see [Reference Robinson15].
While we often make it explicit in the text, throughout we will assume groups to be countable and discrete.
Clearly, for any subshift X, the set of automorphisms of X forms a group under the operation of composition, and we denote this group by
![]() $\mathrm {Aut}(X,\sigma )$
. Since
$\mathrm {Aut}(X,\sigma )$
. Since
![]() $\sigma $
is itself in
$\sigma $
is itself in
![]() $\mathrm {Aut}(X,\sigma )$
and all automorphisms commute with
$\mathrm {Aut}(X,\sigma )$
and all automorphisms commute with
![]() $\sigma $
by definition, the subgroup of
$\sigma $
by definition, the subgroup of
![]() $\mathrm {Aut}(X,\sigma )$
generated by
$\mathrm {Aut}(X,\sigma )$
generated by
![]() $\sigma $
is always normal in
$\sigma $
is always normal in
![]() $\mathrm {Aut}(X,\sigma )$
, and so we may refer to
$\mathrm {Aut}(X,\sigma )$
, and so we may refer to
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
. We refer to the set (generally not a group) of automorphisms with range n by
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
. We refer to the set (generally not a group) of automorphisms with range n by
![]() $\mathrm {Aut}_n(X, \sigma )$
.
$\mathrm {Aut}_n(X, \sigma )$
.
Definition 2.16. For a subset S of a group G, we denote by
![]() $\langle S \rangle $
the subgroup of G generated by S. A group G is said to be generated by
$\langle S \rangle $
the subgroup of G generated by S. A group G is said to be generated by
![]() $S \subset G$
if
$S \subset G$
if
![]() $\langle S \rangle = G$
; such a set S is then said to be a generating subset for G. A group G is finitely generated if there exists a finite
$\langle S \rangle = G$
; such a set S is then said to be a generating subset for G. A group G is finitely generated if there exists a finite
![]() $S \subset G$
for which
$S \subset G$
for which
![]() $G = \langle S \rangle $
. We call a generating subset
$G = \langle S \rangle $
. We call a generating subset
![]() $S \subset G$
symmetric if
$S \subset G$
symmetric if
![]() $S = S^{-1}$
.
$S = S^{-1}$
.
Definition 2.17. A group G is called locally finite if every finitely generated subgroup of G is finite.
Any countable and locally finite group may be written as a countable increasing union of finite subgroups.
Definition 2.18. A group G is called periodic if every element in G has finite order.
Definition 2.19. A countable group G is amenable if there exists a sequence
![]() $F_{i} \subset G$
of finite subsets of G such that, for every
$F_{i} \subset G$
of finite subsets of G such that, for every
![]() $g \in G$
,
$g \in G$
,
 $$ \begin{align*} \lim_{i \to \infty}\frac{|F_{i} \Delta gF_{i}|}{|F_{i}|}=0. \end{align*} $$
$$ \begin{align*} \lim_{i \to \infty}\frac{|F_{i} \Delta gF_{i}|}{|F_{i}|}=0. \end{align*} $$
Definition 2.20. A group G is nilpotent if there exists a sequence of subgroups
such that each
![]() $H_{i}$
is normal in G and
$H_{i}$
is normal in G and
![]() $H_{i+1}/H_{i}$
is contained in the center of
$H_{i+1}/H_{i}$
is contained in the center of
![]() $G/H_{i}$
for all i. A group G is virtually nilpotent if it contains a finite index nilpotent subgroup.
$G/H_{i}$
for all i. A group G is virtually nilpotent if it contains a finite index nilpotent subgroup.
As noted in the introduction, there has been significant recent work on restrictions on
![]() $\mathrm {Aut}(X,\sigma )$
imposed by the word complexity function of X. We mention one such result here which we will need in our proofs.
$\mathrm {Aut}(X,\sigma )$
imposed by the word complexity function of X. We mention one such result here which we will need in our proofs.
Theorem 2.21. [Reference Cyr and Kra5]
If X is a transitive subshift and
![]() ${c_n(X)}/{n^2} \rightarrow 0$
, then
${c_n(X)}/{n^2} \rightarrow 0$
, then
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is a periodic group.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is a periodic group.
Remark 2.22. Theorem 2.21 is not necessarily true if one drops the transitivity assumption on the subshift, even when the complexity function grows linearly (here, by a complexity function growing linearly, we mean it is bounded above by some linear function). For example, if
![]() $(X_{1},\sigma _{1})$
and
$(X_{1},\sigma _{1})$
and
![]() $(X_{2},\sigma _{2})$
are two disjoint infinite subshifts whose complexity functions grow linearly and
$(X_{2},\sigma _{2})$
are two disjoint infinite subshifts whose complexity functions grow linearly and
![]() $(Y,\sigma _{Y})$
is the union of
$(Y,\sigma _{Y})$
is the union of
![]() $(X_{1},\sigma _{1})$
and
$(X_{1},\sigma _{1})$
and
![]() $(X_{2},\sigma _{2})$
, then the complexity function for
$(X_{2},\sigma _{2})$
, then the complexity function for
![]() $(Y,\sigma _{Y})$
also grows linearly. However,
$(Y,\sigma _{Y})$
also grows linearly. However,
![]() ${\mathrm {Aut}(Y,\sigma _{Y})}/{\langle \sigma _{Y} \rangle }$
is not a periodic group: we may define an automorphism
${\mathrm {Aut}(Y,\sigma _{Y})}/{\langle \sigma _{Y} \rangle }$
is not a periodic group: we may define an automorphism
![]() $\phi $
of Y which acts as
$\phi $
of Y which acts as
![]() $\sigma $
on
$\sigma $
on
![]() $X_1$
and the identity on
$X_1$
and the identity on
![]() $X_2$
, and then the image of
$X_2$
, and then the image of
![]() $\phi $
under the map
$\phi $
under the map
![]() $\mathrm {Aut}(Y, \sigma _{Y}) \to {\mathrm {Aut}(Y,\sigma _{Y})}/{\langle \sigma _{Y} \rangle }$
is of infinite order.
$\mathrm {Aut}(Y, \sigma _{Y}) \to {\mathrm {Aut}(Y,\sigma _{Y})}/{\langle \sigma _{Y} \rangle }$
is of infinite order.
2.3 Geometric group theory
We summarize here some basic results from geometric group theory that we will need. For a more detailed introduction to this area, see [Reference Löh13].
Definition 2.23. For any group G generated by a finite symmetric set S and any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $B_n(S)$
denotes the set of ‘words of length at most n over S,’ that is
$B_n(S)$
denotes the set of ‘words of length at most n over S,’ that is
Definition 2.24. A finitely generated group G has polynomial growth if there exists a finite symmetric generating set S and constants C and d so that
![]() $|B_n(S)| < Cn^d$
for all n.
$|B_n(S)| < Cn^d$
for all n.
It is well known that all virtually nilpotent groups have polynomial growth. A celebrated theorem of Gromov shows that the converse is also true.
Theorem 2.25. [Reference Gromov11]
If G is a finitely generated group with polynomial growth, then G is virtually nilpotent.
The following theorem of Shalom and Tao shows that there is an explicit superpolynomial rate below which growth rates must be polynomial.
Theorem 2.26. [Reference Shalom and Tao18, Corollary 1.10]
There exists a constant
![]() $c> 0$
so that if G is a group generated by a finite symmetric subset S, and there exists
$c> 0$
so that if G is a group generated by a finite symmetric subset S, and there exists
![]() $N> c^{-1}$
for which
$N> c^{-1}$
for which
![]() $|B_{N}(S)| \leq N^{c (\log \log N)^c}$
, then G is virtually nilpotent.
$|B_{N}(S)| \leq N^{c (\log \log N)^c}$
, then G is virtually nilpotent.
Although Theorem 2.26 is the first result that gives an explicit ‘gap’ in growth rates for finitely generated groups (that is there is no finitely generated group with growth greater than polynomial but lower than
![]() $N^{c (\log \log n)^c}$
), it is conjectured that this gap is much larger. The gap conjecture [Reference Grigorchuk9] states that if a group has finite symmetric generating set S and
$N^{c (\log \log n)^c}$
), it is conjectured that this gap is much larger. The gap conjecture [Reference Grigorchuk9] states that if a group has finite symmetric generating set S and
![]() $|B_n(S)| = e^{o(\sqrt {n})}$
, then in fact G has polynomial growth (and is therefore virtually nilpotent by Gromov’s theorem). The gap conjecture is still open, but it is known to hold for some classes of groups [Reference Grigorchuk9, Reference Grigorchuk10, Reference Wilson19, Reference Wilson20].
$|B_n(S)| = e^{o(\sqrt {n})}$
, then in fact G has polynomial growth (and is therefore virtually nilpotent by Gromov’s theorem). The gap conjecture is still open, but it is known to hold for some classes of groups [Reference Grigorchuk9, Reference Grigorchuk10, Reference Wilson19, Reference Wilson20].
Definition 2.27. A finitely generated group G has subexponential growth if there exists a finite symmetric generating set S so that
![]() ${\log |B_n(S)|}/{n} \rightarrow 0$
.
${\log |B_n(S)|}/{n} \rightarrow 0$
.
It is well known that finitely generated groups of subexponential growth must be amenable (for instance, see [Reference Löh13, Corollary 9.2.4]).
3
 $\mathrm {Aut}(X,\sigma )$
in the low complexity setting
$\mathrm {Aut}(X,\sigma )$
in the low complexity setting
In this section, we prove Theorems 1.1–1.4. The main tool for Theorems 1.1–1.3 is Theorem 2.26, combined with the following lemma, which bounds the number of automorphisms of a given range.
Corollary 3.1. For every infinite transitive subshift X and every n,
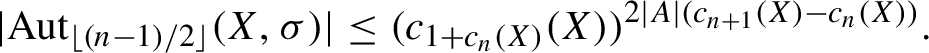 $$ \begin{align*} |\mathrm{Aut}_{\lfloor (n-1)/2 \rfloor}(X, \sigma)| \leq (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))}. \end{align*} $$
$$ \begin{align*} |\mathrm{Aut}_{\lfloor (n-1)/2 \rfloor}(X, \sigma)| \leq (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))}. \end{align*} $$
This is actually a corollary of the following slightly more general theorem, which we will need for Theorem 1.4.
For any subshift X, define
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma ) \subset \mathrm {Aut}(X,\sigma )$
to be the subgroup of automorphisms of X which fix all isolated periodic points in X. (If X has no isolated periodic points, then
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma ) \subset \mathrm {Aut}(X,\sigma )$
to be the subgroup of automorphisms of X which fix all isolated periodic points in X. (If X has no isolated periodic points, then
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma ) := \mathrm {Aut}(X,\sigma )$
.) We denote the set of such automorphisms which have range n by
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma ) := \mathrm {Aut}(X,\sigma )$
.) We denote the set of such automorphisms which have range n by
 $\mathrm {Aut}^{(\textit{FIP})}_n(X, \sigma )$
.
$\mathrm {Aut}^{(\textit{FIP})}_n(X, \sigma )$
.
Theorem 3.2. Let X be a subshift. Then for every n,
 $$ \begin{align*} |\mathrm{Aut}^{(\textit{FIP})}_{\lfloor (n-1)/2 \rfloor}(X, \sigma)| \leq (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))}. \end{align*} $$
$$ \begin{align*} |\mathrm{Aut}^{(\textit{FIP})}_{\lfloor (n-1)/2 \rfloor}(X, \sigma)| \leq (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))}. \end{align*} $$
Proof. For any subshift X and any n, define an n-right branch word to be a word in
![]() $L(X)$
beginning with a word in
$L(X)$
beginning with a word in
![]() $RS_n(X)$
, containing no other word in
$RS_n(X)$
, containing no other word in
![]() $RS_n(X)$
, containing no repeated n-letter subwords, and which is maximal with respect to subword inclusion subject to these constraints. Similarly, define an n-left branch word to be a word in
$RS_n(X)$
, containing no repeated n-letter subwords, and which is maximal with respect to subword inclusion subject to these constraints. Similarly, define an n-left branch word to be a word in
![]() $L(X)$
ending with a word in
$L(X)$
ending with a word in
![]() $LS_n(X)$
, containing no other word in
$LS_n(X)$
, containing no other word in
![]() $LS_n(X)$
, with no repeated n-letter subwords, and which is maximal with respect to subword inclusion subject to these constraints. An n-branch word is any word that is either an n-left or n-right branch word.
$LS_n(X)$
, with no repeated n-letter subwords, and which is maximal with respect to subword inclusion subject to these constraints. An n-branch word is any word that is either an n-left or n-right branch word.
The proof relies on the following three facts about n-branch words.
-
(1) For every n, the number of n-branch words is less than or equal to the quantity
 $2|A| (c_{n+1}(X) - c_n(X))$
.
$2|A| (c_{n+1}(X) - c_n(X))$
. -
(2) For every n, each n-branch word has length less than
 $n + c_n(X)$
.
$n + c_n(X)$
. -
(3) Suppose
 $\phi _1$
and
$\phi _1$
and
 $\phi _2$
are automorphisms with range
$\phi _2$
are automorphisms with range
 $\lfloor (n-1)/2 \rfloor $
induced by block codes
$\lfloor (n-1)/2 \rfloor $
induced by block codes
 $\Phi _{1}, \Phi _{2}$
respectively such that
$\Phi _{1}, \Phi _{2}$
respectively such that
 $\phi _{1}, \phi _{2}$
fix all isolated periodic points, and
$\phi _{1}, \phi _{2}$
fix all isolated periodic points, and
 $\Phi _1(w) = \Phi _2(w)$
for all n-branch words w. Then
$\Phi _1(w) = \Phi _2(w)$
for all n-branch words w. Then
 $\phi _1 = \phi _2$
.
$\phi _1 = \phi _2$
.
Proof of fact (1). Each n-right branch word w is determined completely by its initial word in
![]() $RS_n(X)$
and the following letter; then, since w contains no other words in
$RS_n(X)$
and the following letter; then, since w contains no other words in
![]() $RS_n(X)$
, each n-letter subword determines the next letter, meaning that all of w is forced. There are obviously at most
$RS_n(X)$
, each n-letter subword determines the next letter, meaning that all of w is forced. There are obviously at most
![]() $|A| |RS_n(X)|$
choices for this initial word and following letter, which is less than or equal to
$|A| |RS_n(X)|$
choices for this initial word and following letter, which is less than or equal to
![]() $|A| (c_{n+1}(X) - c_n(X))$
by Lemma 2.9. A similar bound holds for n-left branch words, implying fact (1).
$|A| (c_{n+1}(X) - c_n(X))$
by Lemma 2.9. A similar bound holds for n-left branch words, implying fact (1).
Proof of fact (2). Every n-branch word contains no repeated n-letter subwords, and so contains at most
![]() $c_n(X) n$
-letter subwords. This clearly implies that such a word has length less than
$c_n(X) n$
-letter subwords. This clearly implies that such a word has length less than
![]() $n + c_n(X)$
.
$n + c_n(X)$
.
Proof of fact (3). We claim that every
![]() $w \kern-1pt\in\kern-1pt L_n(X)$
which is not the subword of any n-branch word must be a subword of an isolated periodic point of X. To see this, assume that
$w \kern-1pt\in\kern-1pt L_n(X)$
which is not the subword of any n-branch word must be a subword of an isolated periodic point of X. To see this, assume that
![]() $w \in L_n(X)$
is not a subword of any n-branch word.
$w \in L_n(X)$
is not a subword of any n-branch word.
Choose any
![]() $x \in X$
with
$x \in X$
with
![]() $x([0, n)) = w$
. Define m to be the minimal integer greater than n so that there exists
$x([0, n)) = w$
. Define m to be the minimal integer greater than n so that there exists
![]() $n \leq i < m$
for which
$n \leq i < m$
for which
![]() $x([i-n, i)) = x([m-n, m))$
, that is the first place, when moving to the right from
$x([i-n, i)) = x([m-n, m))$
, that is the first place, when moving to the right from
![]() $x(0)$
, where an n-letter word appears for the second time. Choose such an i, and suppose
$x(0)$
, where an n-letter word appears for the second time. Choose such an i, and suppose
![]() $i> n$
. Then
$i> n$
. Then
![]() $x(i-n-1) \neq x(m-n-1)$
, since otherwise,
$x(i-n-1) \neq x(m-n-1)$
, since otherwise,
![]() $x([i-n-1, i-1)) = x([m-n-1, m-1))$
, violating minimality of m. This would imply that
$x([i-n-1, i-1)) = x([m-n-1, m-1))$
, violating minimality of m. This would imply that
![]() $x([i-n, i))$
is a left-special word, and by minimality of m, that
$x([i-n, i))$
is a left-special word, and by minimality of m, that
![]() $x([0,i))$
is a word ending with a word in
$x([0,i))$
is a word ending with a word in
![]() $LS_n(X)$
with no repeated n-letter subwords. We could then extend
$LS_n(X)$
with no repeated n-letter subwords. We could then extend
![]() $x([0,i))$
to the left to create a maximal such word
$x([0,i))$
to the left to create a maximal such word
![]() $x([j,i))$
, which is an n-left branch word by definition. This n-left branch word would contain
$x([j,i))$
, which is an n-left branch word by definition. This n-left branch word would contain
![]() $w = x([0,n))$
as a subword, a contradiction.
$w = x([0,n))$
as a subword, a contradiction.
Therefore
![]() $i = n$
, that is
$i = n$
, that is
![]() $x([0, m))$
begins and ends with w. If
$x([0, m))$
begins and ends with w. If
![]() $x([0, m))$
contained any words in
$x([0, m))$
contained any words in
![]() $LS_n(X)$
, then just as before we could construct an n-left branch word containing w, a contradiction. We have then shown that
$LS_n(X)$
, then just as before we could construct an n-left branch word containing w, a contradiction. We have then shown that
![]() $x([0,m))$
begins and ends with w and contains no subwords in
$x([0,m))$
begins and ends with w and contains no subwords in
![]() $LS_n(X)$
. Therefore, the right-most occurrence of w in
$LS_n(X)$
. Therefore, the right-most occurrence of w in
![]() $x([0,m))$
forces letters to the left until the left-most occurrence of w, and this continues indefinitely. In other words, every
$x([0,m))$
forces letters to the left until the left-most occurrence of w, and this continues indefinitely. In other words, every
![]() $y \in X$
with
$y \in X$
with
![]() $y([0,m)) = x([0,m))$
in fact has
$y([0,m)) = x([0,m))$
in fact has
![]() $y((-\infty , m))$
periodic with period
$y((-\infty , m))$
periodic with period
![]() $m-n$
.
$m-n$
.
A similar argument shows that
![]() $x([0,m))$
cannot contain any words in
$x([0,m))$
cannot contain any words in
![]() $RS_n(X)$
either; if
$RS_n(X)$
either; if
![]() $j \geq 0$
were minimal so that
$j \geq 0$
were minimal so that
![]() $x([j, m))$
begins with a word in
$x([j, m))$
begins with a word in
![]() $RS_n(X)$
, then
$RS_n(X)$
, then
![]() $x([j,m))$
could be extended to the right to create an n-right branch word containing
$x([j,m))$
could be extended to the right to create an n-right branch word containing
![]() $x([m-n, m)) = w$
, a contradiction. So
$x([m-n, m)) = w$
, a contradiction. So
![]() $x([0,m))$
contains no words in
$x([0,m))$
contains no words in
![]() $RS_n(X)$
, meaning that the left-most occurrence of w forces letters to the right until the right-most occurrence. It follows that if
$RS_n(X)$
, meaning that the left-most occurrence of w forces letters to the right until the right-most occurrence. It follows that if
![]() $y \in X$
satisfies
$y \in X$
satisfies
![]() $y([0,m)) = x([0,m))$
, then
$y([0,m)) = x([0,m))$
, then
![]() $y([0, \infty ))$
is periodic with period
$y([0, \infty ))$
is periodic with period
![]() $m-n$
.
$m-n$
.
Altogether, what we have shown is that every
![]() $y \in X$
with
$y \in X$
with
![]() $y([0, m)) = x([0, m))$
is a periodic point with period
$y([0, m)) = x([0, m))$
is a periodic point with period
![]() $m-n$
coming from biinfinite repetition of
$m-n$
coming from biinfinite repetition of
![]() $x([0, m-n))$
. Therefore, x is an isolated periodic point, verifying the claim that every
$x([0, m-n))$
. Therefore, x is an isolated periodic point, verifying the claim that every
![]() $w \in L_n(X)$
which is not the subword of any n-branch word must be a subword of an isolated periodic point.
$w \in L_n(X)$
which is not the subword of any n-branch word must be a subword of an isolated periodic point.
Now, choose any
![]() $\phi _1,\phi _2 \in \mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
with range
$\phi _1,\phi _2 \in \mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
with range
![]() $\lfloor (n-1)/2 \rfloor $
and inducing block maps
$\lfloor (n-1)/2 \rfloor $
and inducing block maps
![]() $\Phi _1$
and
$\Phi _1$
and
![]() $\Phi _2$
, and assume that
$\Phi _2$
, and assume that
![]() $\Phi _{1}(v) = \Phi _{2}(v)$
for all n-branch words v. Define
$\Phi _{1}(v) = \Phi _{2}(v)$
for all n-branch words v. Define
![]() $n' = 2 \lfloor (n-1)/2 \rfloor + 1$
, so that
$n' = 2 \lfloor (n-1)/2 \rfloor + 1$
, so that
![]() $\Phi _1$
and
$\Phi _1$
and
![]() $\Phi _2$
have domain
$\Phi _2$
have domain
![]() $\mathcal {A}^{n'}$
; clearly
$\mathcal {A}^{n'}$
; clearly
![]() $n' \leq n$
. Since
$n' \leq n$
. Since
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
fix isolated periodic points, for all
$\phi _2$
fix isolated periodic points, for all
![]() $n'$
-letter subwords u of such points,
$n'$
-letter subwords u of such points,
![]() $\Phi _1(u) = \Phi _2(u)$
. Choose any
$\Phi _1(u) = \Phi _2(u)$
. Choose any
![]() $w \in L_{n'}(X)$
which is not a subword of such a point; since
$w \in L_{n'}(X)$
which is not a subword of such a point; since
![]() $n' \leq n$
, by the above, it is a subword of an n-branch word v. Now, since
$n' \leq n$
, by the above, it is a subword of an n-branch word v. Now, since
![]() $\Phi _{1}(v) = \Phi _{2}(v)$
and w is a subword of v,
$\Phi _{1}(v) = \Phi _{2}(v)$
and w is a subword of v,
![]() $\Phi _1(w) = \Phi _2(w)$
. We now know that
$\Phi _1(w) = \Phi _2(w)$
. We now know that
![]() $\Phi _1$
and
$\Phi _1$
and
![]() $\Phi _2$
agree on all words in
$\Phi _2$
agree on all words in
![]() $L_{n'}(X)$
, so
$L_{n'}(X)$
, so
![]() $\Phi _1 = \Phi _2$
, meaning that
$\Phi _1 = \Phi _2$
, meaning that
![]() $\phi _1 = \phi _2$
.
$\phi _1 = \phi _2$
.
By fact (3), the number of automorphisms of range
![]() $\lfloor (n-1)/2 \rfloor $
which fix isolated periodic points is bounded from above by the number of possible choices for
$\lfloor (n-1)/2 \rfloor $
which fix isolated periodic points is bounded from above by the number of possible choices for
![]() $\Phi (w)$
for all n-branch words w. Each
$\Phi (w)$
for all n-branch words w. Each
![]() $\Phi (w)$
is determined by the length of w (which is independent of
$\Phi (w)$
is determined by the length of w (which is independent of
![]() $\phi $
) and some word of length
$\phi $
) and some word of length
![]() $|w| - 2\lfloor (n-1)/2 \rfloor \leq |w| - n + 2$
. By fact (2), the number of such words is less than or equal to
$|w| - 2\lfloor (n-1)/2 \rfloor \leq |w| - n + 2$
. By fact (2), the number of such words is less than or equal to
![]() $c_{1+c_n(X)}(X)$
. By fact (1), the number of w is bounded by
$c_{1+c_n(X)}(X)$
. By fact (1), the number of w is bounded by
![]() $2|A| (c_{n+1}(X) - c_n(X))$
, completing the proof.
$2|A| (c_{n+1}(X) - c_n(X))$
, completing the proof.
Corollary 3.1 now follows immediately since an infinite transitive subshift X has no isolated points.
We will also need the following technical lemma, which will allow us to use low complexity along a subsequence to prove the existence of a (possibly sparser) subsequence where both complexity and first difference of complexity are small.
Lemma 3.3. For any sequences of positive reals
![]() $f(n)$
and
$f(n)$
and
![]() $g(n)$
where
$g(n)$
where
 $$ \begin{align*} \liminf f(n) - \sum_{i=1}^n g(i) = -\infty, \end{align*} $$
$$ \begin{align*} \liminf f(n) - \sum_{i=1}^n g(i) = -\infty, \end{align*} $$
there exist infinitely many values of n where
![]() $f(n) < \sum _{i=1}^n g(i)$
and
$f(n) < \sum _{i=1}^n g(i)$
and
![]() $f(n) - f(n-1) < g(n)$
.
$f(n) - f(n-1) < g(n)$
.
Proof. We first note that the hypothesis immediately implies that there exist infinitely many n where
![]() $f(n) - f(n-1) < g(n)$
; if not, then there would be N where
$f(n) - f(n-1) < g(n)$
; if not, then there would be N where
![]() $f(n) - f(n-1) \geq g(n)$
for all
$f(n) - f(n-1) \geq g(n)$
for all
![]() $n> N$
, meaning that
$n> N$
, meaning that
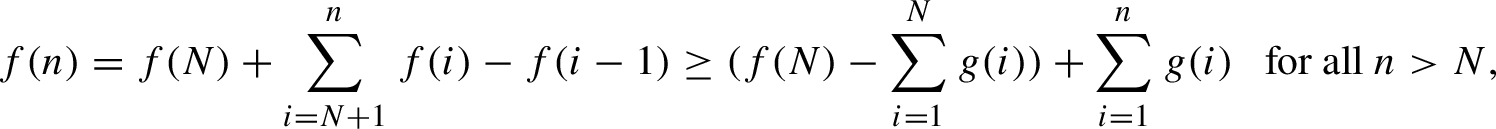 $$ \begin{align*} f(n) = f(N) + \sum_{i=N+1}^{n} f(i) - f(i-1) \geq (f(N) - \sum_{i=1}^{N} g(i)) + \sum_{i=1}^n g(i)\ \ \ \mathrm{for\ all }\ n> N, \end{align*} $$
$$ \begin{align*} f(n) = f(N) + \sum_{i=N+1}^{n} f(i) - f(i-1) \geq (f(N) - \sum_{i=1}^{N} g(i)) + \sum_{i=1}^n g(i)\ \ \ \mathrm{for\ all }\ n> N, \end{align*} $$
a contradiction to the assumption.
We now break into two cases. First, suppose that there exists N so that
![]() $f(n) < \sum _{i=1}^n g(i)$
for
$f(n) < \sum _{i=1}^n g(i)$
for
![]() $n> N$
. Combining with the previous paragraph then yields the conclusion of the lemma.
$n> N$
. Combining with the previous paragraph then yields the conclusion of the lemma.
Now, suppose that there exist infinitely many n where
![]() $f(n) \geq \sum _{i = 1}^{n} g(i)$
. The hypothesis of the lemma implies that there are also infinitely many n where
$f(n) \geq \sum _{i = 1}^{n} g(i)$
. The hypothesis of the lemma implies that there are also infinitely many n where
![]() $f(n) < \sum _{i=1}^n g(i)$
. This implies that there are infinitely many n where
$f(n) < \sum _{i=1}^n g(i)$
. This implies that there are infinitely many n where
 $f(n-1) \geq \sum _{i=1}^{n-1} g(i)$
and
$f(n-1) \geq \sum _{i=1}^{n-1} g(i)$
and
![]() $f(n) < \sum _{i=1}^{n} g(i)$
(that is the sign of the inequality ‘switches infinitely many times’). However, for any such n,
$f(n) < \sum _{i=1}^{n} g(i)$
(that is the sign of the inequality ‘switches infinitely many times’). However, for any such n,
 $$ \begin{align*} f(n) - f(n-1) < \sum_{i=1}^{n} g(i) - \sum_{i=1}^{n-1} g(i) = g(n), \end{align*} $$
$$ \begin{align*} f(n) - f(n-1) < \sum_{i=1}^{n} g(i) - \sum_{i=1}^{n-1} g(i) = g(n), \end{align*} $$
completing the proof.
We are now prepared to prove Theorems 1.1–1.4. We briefly note that if X is finite, then
![]() $\mathrm {Aut}(X,\sigma )$
and
$\mathrm {Aut}(X,\sigma )$
and
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
are finite, and the conclusions of these theorems trivially hold. We therefore treat only the case where X is infinite in all proofs.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
are finite, and the conclusions of these theorems trivially hold. We therefore treat only the case where X is infinite in all proofs.
Proof of Theorem 1.1
Choose any infinite transitive subshift X with
![]() $\liminf (\log (c_n(X)/n) / (\log \log \log n)) = 0$
, and take
$\liminf (\log (c_n(X)/n) / (\log \log \log n)) = 0$
, and take
![]() $\epsilon> 0$
where
$\epsilon> 0$
where
![]() $5\epsilon $
is less than the constant c from Theorem 2.26. We first claim that
$5\epsilon $
is less than the constant c from Theorem 2.26. We first claim that
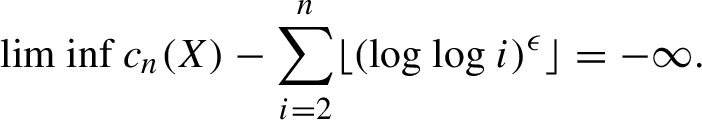 $$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor (\log \log i)^{\epsilon} \rfloor = -\infty. \end{align} $$
$$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor (\log \log i)^{\epsilon} \rfloor = -\infty. \end{align} $$
To see this, by assumption, there are infinitely many n where
![]() $c_n(X) < n (\log \log n)^{\epsilon /2}$
, which is less than
$c_n(X) < n (\log \log n)^{\epsilon /2}$
, which is less than
![]() $(n/3) (\log \log (n/2))^{\epsilon }$
for large enough n. Also,
$(n/3) (\log \log (n/2))^{\epsilon }$
for large enough n. Also,
 $\sum _{i = 2}^n \lfloor (\log \log i)^{\epsilon } \rfloor \geq \sum _{i = \lceil n/2 \rceil }^n \lfloor (\log \log i)^{\epsilon } \rfloor \geq (n/2) \lfloor (\log \log (n/2))^{\epsilon } \rfloor $
, and so for infinitely many n,
$\sum _{i = 2}^n \lfloor (\log \log i)^{\epsilon } \rfloor \geq \sum _{i = \lceil n/2 \rceil }^n \lfloor (\log \log i)^{\epsilon } \rfloor \geq (n/2) \lfloor (\log \log (n/2))^{\epsilon } \rfloor $
, and so for infinitely many n,
![]() $c_n(X) - \sum _{i = 2}^n \lfloor (\log \log i)^{\epsilon } \rfloor $
is less than
$c_n(X) - \sum _{i = 2}^n \lfloor (\log \log i)^{\epsilon } \rfloor $
is less than
which approaches
![]() $-\infty $
, verifying equation (1). We now apply Lemma 3.3, and see that there exist infinitely many n for which
$-\infty $
, verifying equation (1). We now apply Lemma 3.3, and see that there exist infinitely many n for which
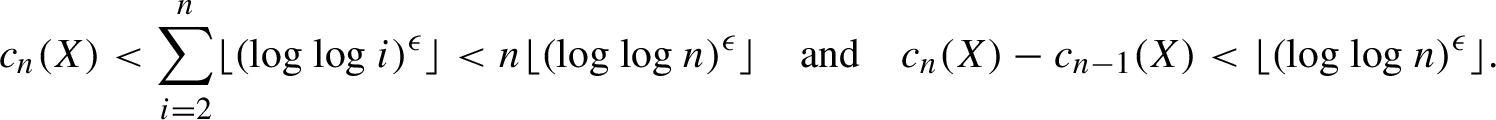 $$ \begin{align} c_n(X) < \sum_{i = 2}^n \lfloor (\log \log i)^{\epsilon} \rfloor < n \lfloor (\log \log n)^{\epsilon} \rfloor \quad\textrm{and}\quad c_n(X) - c_{n-1}(X) < \lfloor (\log \log n)^{\epsilon} \rfloor. \end{align} $$
$$ \begin{align} c_n(X) < \sum_{i = 2}^n \lfloor (\log \log i)^{\epsilon} \rfloor < n \lfloor (\log \log n)^{\epsilon} \rfloor \quad\textrm{and}\quad c_n(X) - c_{n-1}(X) < \lfloor (\log \log n)^{\epsilon} \rfloor. \end{align} $$
Now, by Corollary 3.1, for any n satisfying equation (2),
![]() $|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
$|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
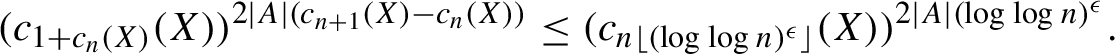 $$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (c_{n\lfloor (\log \log n)^{\epsilon}\rfloor}(X))^{2|A| (\log \log n)^{\epsilon}}. \end{align*} $$
$$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (c_{n\lfloor (\log \log n)^{\epsilon}\rfloor}(X))^{2|A| (\log \log n)^{\epsilon}}. \end{align*} $$
By subadditivity,
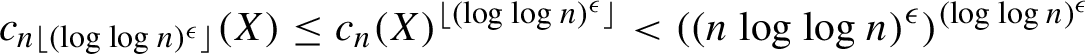 $$ \begin{align*} c_{n\lfloor (\log \log n)^{\epsilon}\rfloor}(X) \leq c_n(X)^{\lfloor (\log \log n)^{\epsilon} \rfloor} < ((n\log \log n)^{\epsilon})^{(\log \log n)^{\epsilon}} \end{align*} $$
$$ \begin{align*} c_{n\lfloor (\log \log n)^{\epsilon}\rfloor}(X) \leq c_n(X)^{\lfloor (\log \log n)^{\epsilon} \rfloor} < ((n\log \log n)^{\epsilon})^{(\log \log n)^{\epsilon}} \end{align*} $$
Therefore,
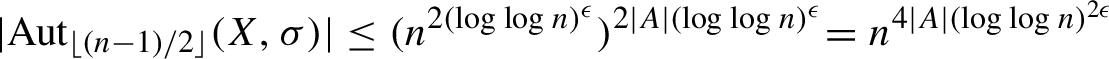 $$ \begin{align} |\mathrm{Aut}_{\lfloor (n-1)/2 \rfloor}(X, \sigma)| \leq (n^{2 (\log \log n)^{\epsilon}})^{2|A| (\log \log n)^{\epsilon}} \!= n^{4|A| (\log \log n)^{2\epsilon}} \end{align} $$
$$ \begin{align} |\mathrm{Aut}_{\lfloor (n-1)/2 \rfloor}(X, \sigma)| \leq (n^{2 (\log \log n)^{\epsilon}})^{2|A| (\log \log n)^{\epsilon}} \!= n^{4|A| (\log \log n)^{2\epsilon}} \end{align} $$
holds for any of the (infinitely many) n satisfying equation (2).
Now, choose any finite subset S of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
and let
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
and let
![]() $S^{\prime }$
be a finite set in
$S^{\prime }$
be a finite set in
![]() $\mathrm {Aut}(X,\sigma )$
whose image under the quotient map
$\mathrm {Aut}(X,\sigma )$
whose image under the quotient map
![]() $\mathrm {Aut}(X,\sigma ) \to {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is the set S. Suppose that k is large enough that all automorphisms in
$\mathrm {Aut}(X,\sigma ) \to {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is the set S. Suppose that k is large enough that all automorphisms in
![]() $S'$
and their inverses have range k. Then by additivity of ranges of automorphisms under composition, any composition of m elements of
$S'$
and their inverses have range k. Then by additivity of ranges of automorphisms under composition, any composition of m elements of
![]() $S'$
is an automorphism of range
$S'$
is an automorphism of range
![]() $km$
.
$km$
.
Then for any n for which equation (2) holds, equation (3) implies that the number
![]() $B_{\lfloor (n-1)/2 \rfloor /k}(S')$
of compositions of at most
$B_{\lfloor (n-1)/2 \rfloor /k}(S')$
of compositions of at most
![]() $\lfloor (n-1)/2 \rfloor /k$
elements of
$\lfloor (n-1)/2 \rfloor /k$
elements of
![]() $S'$
satisfies
$S'$
satisfies
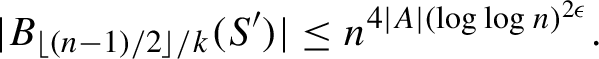 $$ \begin{align*} |B_{\lfloor (n-1)/2 \rfloor/k}(S')| \leq n^{4|A| (\log \log n)^{2\epsilon}}. \end{align*} $$
$$ \begin{align*} |B_{\lfloor (n-1)/2 \rfloor/k}(S')| \leq n^{4|A| (\log \log n)^{2\epsilon}}. \end{align*} $$
Since equation (2) holds for infinitely many n, we may choose such an n greater than
![]() $e^{e^3}$
,
$e^{e^3}$
,
![]() $9k^2$
,
$9k^2$
,
 $e^{2e^{(8|A|/5\epsilon )^{\epsilon ^{-1}}}}$
, and
$e^{2e^{(8|A|/5\epsilon )^{\epsilon ^{-1}}}}$
, and
![]() $c^{-2}$
(here c is as in Theorem 2.26). Then
$c^{-2}$
(here c is as in Theorem 2.26). Then
![]() $\lfloor (n-1)/2 \rfloor /k> n/3k > \sqrt {n}$
, and
$\lfloor (n-1)/2 \rfloor /k> n/3k > \sqrt {n}$
, and
 $\log \log \sqrt {n} = \log \log n - \log 2> \sqrt {\log \log n}$
since
$\log \log \sqrt {n} = \log \log n - \log 2> \sqrt {\log \log n}$
since
![]() $\log \log n> 3$
, so
$\log \log n> 3$
, so
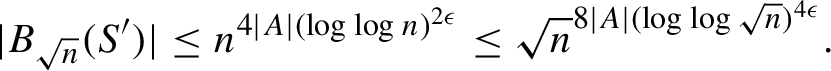 $$ \begin{align*} |B_{\sqrt{n}}(S')| \leq n^{4|A| (\log \log n)^{2\epsilon}} \leq \sqrt{n}^{8|A| (\log \log \sqrt{n})^{4\epsilon}}. \end{align*} $$
$$ \begin{align*} |B_{\sqrt{n}}(S')| \leq n^{4|A| (\log \log n)^{2\epsilon}} \leq \sqrt{n}^{8|A| (\log \log \sqrt{n})^{4\epsilon}}. \end{align*} $$
Since
 $n> e^{2e^{(8|A|/5\epsilon )^{\epsilon ^{-1}}}}$
, then
$n> e^{2e^{(8|A|/5\epsilon )^{\epsilon ^{-1}}}}$
, then
![]() $8|A| < 5 \epsilon (\log \log \sqrt {n})^{\epsilon }$
, and so
$8|A| < 5 \epsilon (\log \log \sqrt {n})^{\epsilon }$
, and so
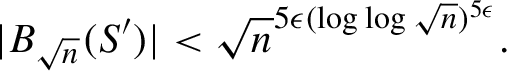 $$ \begin{align*} |B_{\sqrt{n}}(S')| < \sqrt{n}^{5\epsilon (\log \log \sqrt{n})^{5\epsilon}}. \end{align*} $$
$$ \begin{align*} |B_{\sqrt{n}}(S')| < \sqrt{n}^{5\epsilon (\log \log \sqrt{n})^{5\epsilon}}. \end{align*} $$
Finally, since
![]() $\sqrt {n}> c^{-1}$
, by Theorem 2.26,
$\sqrt {n}> c^{-1}$
, by Theorem 2.26,
![]() $\langle S' \rangle $
is virtually nilpotent.
$\langle S' \rangle $
is virtually nilpotent.
Therefore,
![]() $\langle S \rangle = {\langle S' \rangle }/{\langle \sigma \rangle }$
is a quotient group of a virtually nilpotent group and so itself virtually nilpotent. Let H be a finite index nilpotent subgroup of
$\langle S \rangle = {\langle S' \rangle }/{\langle \sigma \rangle }$
is a quotient group of a virtually nilpotent group and so itself virtually nilpotent. Let H be a finite index nilpotent subgroup of
![]() $\langle S \rangle $
; it is finitely generated as it is a finite index subgroup of a finitely generated group. By Theorem 2.21,
$\langle S \rangle $
; it is finitely generated as it is a finite index subgroup of a finitely generated group. By Theorem 2.21,
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is periodic, so H is also periodic. Altogether we have that H is finitely generated, periodic, and nilpotent, and therefore finite, implying that
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is periodic, so H is also periodic. Altogether we have that H is finitely generated, periodic, and nilpotent, and therefore finite, implying that
![]() $\langle S \rangle $
is finite as well. Since S was an arbitrary finite subset of
$\langle S \rangle $
is finite as well. Since S was an arbitrary finite subset of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
, we have shown that
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
, we have shown that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
Proof of Theorem 1.2
Assume that the gap conjecture holds. We change almost nothing about the proof of Theorem 1.1, but must simply change our estimates for the usage of Lemma 3.3.
Choose any infinite transitive subshift X where
![]() $\liminf ({c_n(X)}/{n^{1.25} (\log n)^{-0.5}}) = 0$
. We first claim that for any
$\liminf ({c_n(X)}/{n^{1.25} (\log n)^{-0.5}}) = 0$
. We first claim that for any
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
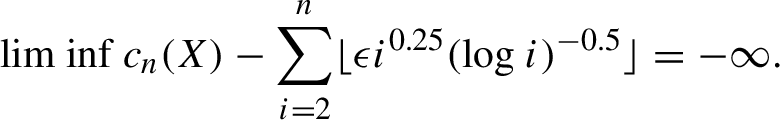 $$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor = -\infty. \end{align} $$
$$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor = -\infty. \end{align} $$
To see this, note that by assumption, there are infinitely many n where
![]() $c_n(X) < ({\epsilon }/{3}) n^{1.25} (\log n)^{-0.5}$
. Also,
$c_n(X) < ({\epsilon }/{3}) n^{1.25} (\log n)^{-0.5}$
. Also,
 $\sum _{i = 2}^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor \geq \sum _{i = \lceil n/2 \rceil }^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor \geq (n/2) \lfloor \epsilon (n/2)^{0.25} (\log n)^{-0.5} \rfloor \geq ({\epsilon }/{2^{1.25}}) n^{1.25} (\log n)^{-0.5} - {n}/{2}$
. So, for infinitely many n,
$\sum _{i = 2}^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor \geq \sum _{i = \lceil n/2 \rceil }^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor \geq (n/2) \lfloor \epsilon (n/2)^{0.25} (\log n)^{-0.5} \rfloor \geq ({\epsilon }/{2^{1.25}}) n^{1.25} (\log n)^{-0.5} - {n}/{2}$
. So, for infinitely many n,
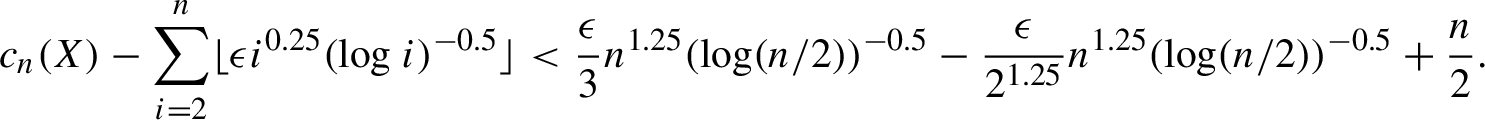 $$ \begin{align*} c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor < \frac{\epsilon }{3} n^{1.25} (\log (n/2))^{-0.5} - \frac{\epsilon }{2^{1.25}} n^{1.25} (\log (n/2))^{-0.5} + \frac{n}{2}. \end{align*} $$
$$ \begin{align*} c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor < \frac{\epsilon }{3} n^{1.25} (\log (n/2))^{-0.5} - \frac{\epsilon }{2^{1.25}} n^{1.25} (\log (n/2))^{-0.5} + \frac{n}{2}. \end{align*} $$
Since this last term approaches
![]() $-\infty $
, we have verified equation (4). We now apply Lemma 3.3, and see that there exist infinitely many n for which
$-\infty $
, we have verified equation (4). We now apply Lemma 3.3, and see that there exist infinitely many n for which
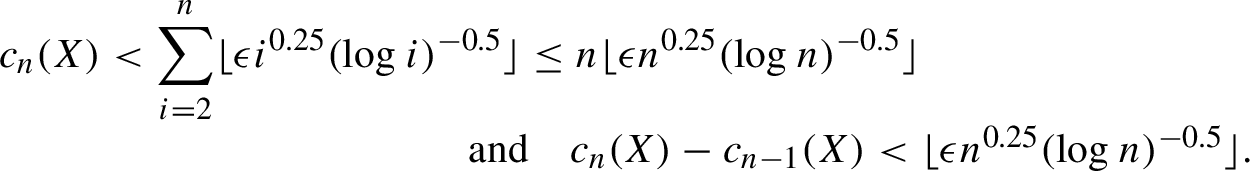 $$ \begin{align} \begin{array}{c} c_n(X) < \displaystyle{\sum_{i = 2}^n} \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor \leq n \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor \qquad\qquad\qquad\qquad\quad \\ \qquad\qquad\qquad\qquad\qquad\quad \textrm{ and}\quad c_n(X) - c_{n-1}(X) < \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor. \end{array}\end{align} $$
$$ \begin{align} \begin{array}{c} c_n(X) < \displaystyle{\sum_{i = 2}^n} \lfloor \epsilon i^{0.25} (\log i)^{-0.5} \rfloor \leq n \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor \qquad\qquad\qquad\qquad\quad \\ \qquad\qquad\qquad\qquad\qquad\quad \textrm{ and}\quad c_n(X) - c_{n-1}(X) < \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor. \end{array}\end{align} $$
Now, by Corollary 3.1, if n satisfies equation (5),
![]() $|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
$|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
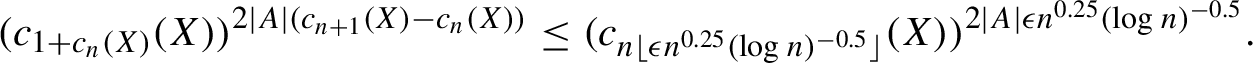 $$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (c_{n \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor}(X))^{2|A| \epsilon n^{0.25} (\log n)^{-0.5}}. \end{align*} $$
$$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (c_{n \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor}(X))^{2|A| \epsilon n^{0.25} (\log n)^{-0.5}}. \end{align*} $$
By subadditivity,
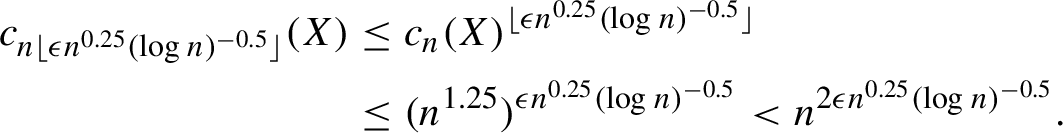 $$ \begin{align*} c_{n \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor}(X) &\leq c_n(X)^{\lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor}\\ &\leq (n^{1.25})^{\epsilon n^{0.25} (\log n)^{-0.5}} < n^{2\epsilon n^{0.25} (\log n)^{-0.5}}. \end{align*} $$
$$ \begin{align*} c_{n \lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor}(X) &\leq c_n(X)^{\lfloor \epsilon n^{0.25} (\log n)^{-0.5} \rfloor}\\ &\leq (n^{1.25})^{\epsilon n^{0.25} (\log n)^{-0.5}} < n^{2\epsilon n^{0.25} (\log n)^{-0.5}}. \end{align*} $$
Therefore,
![]() $|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
$|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
 $$ \begin{align*} (n^{2\epsilon n^{0.25} (\log n)^{-0.5}})^{2|A|\epsilon n^{0.25} (\log n)^{-0.5}} = n^{4|A| \epsilon^2 n^{0.5} (\log n)^{-1}} = e^{4|A| \epsilon^2 \sqrt{n}}. \end{align*} $$
$$ \begin{align*} (n^{2\epsilon n^{0.25} (\log n)^{-0.5}})^{2|A|\epsilon n^{0.25} (\log n)^{-0.5}} = n^{4|A| \epsilon^2 n^{0.5} (\log n)^{-1}} = e^{4|A| \epsilon^2 \sqrt{n}}. \end{align*} $$
Now, exactly as in the end of Theorem 1.1, any finitely generated subgroup H of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
has growth less than
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
has growth less than
![]() $e^{4|A| \epsilon ^2 \sqrt {n}}$
. Since
$e^{4|A| \epsilon ^2 \sqrt {n}}$
. Since
![]() $\epsilon> 0$
was arbitrary, by the gap conjecture, H must be virtually nilpotent. Exactly as in the proof of Theorem 1.1, this implies that
$\epsilon> 0$
was arbitrary, by the gap conjecture, H must be virtually nilpotent. Exactly as in the proof of Theorem 1.1, this implies that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
Proof of Theorem 1.3
Assume that the gap conjecture holds, and choose any infinite transitive subshift X where
![]() ${c_n(X)}/{n^{1.5} (\log n)^{-1}} \rightarrow 0$
. We first claim that for any
${c_n(X)}/{n^{1.5} (\log n)^{-1}} \rightarrow 0$
. We first claim that for any
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
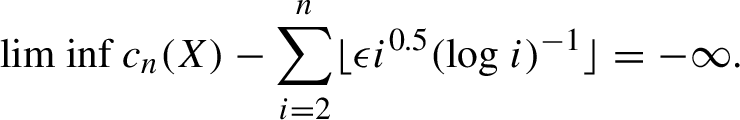 $$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i^{0.5} (\log i)^{-1}\rfloor = -\infty. \end{align} $$
$$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i^{0.5} (\log i)^{-1}\rfloor = -\infty. \end{align} $$
Again, by assumption, there are infinitely many n where
![]() $c_n(X) < ({\epsilon }/{3}) n^{1.5} (\log n)^{-1}$
. Also,
$c_n(X) < ({\epsilon }/{3}) n^{1.5} (\log n)^{-1}$
. Also,
 $\sum _{i = 2}^n \lfloor \epsilon i^{0.5} (\log i)^{-1} \rfloor \geq \sum _{i = \lceil n/2 \rceil }^n \lfloor \epsilon i^{0.5} (\log i)^{-1} \rfloor \geq (n/2) \lfloor \epsilon (n/2)^{0.5} (\log n)^{-1} \rfloor \geq ({\epsilon }/{2^{1.5}}) n^{1.5} (\log n)^{-1} \kern1.2pt{-}\kern1.2pt {n}/{2}$
. So, for infinitely many n,
$\sum _{i = 2}^n \lfloor \epsilon i^{0.5} (\log i)^{-1} \rfloor \geq \sum _{i = \lceil n/2 \rceil }^n \lfloor \epsilon i^{0.5} (\log i)^{-1} \rfloor \geq (n/2) \lfloor \epsilon (n/2)^{0.5} (\log n)^{-1} \rfloor \geq ({\epsilon }/{2^{1.5}}) n^{1.5} (\log n)^{-1} \kern1.2pt{-}\kern1.2pt {n}/{2}$
. So, for infinitely many n,
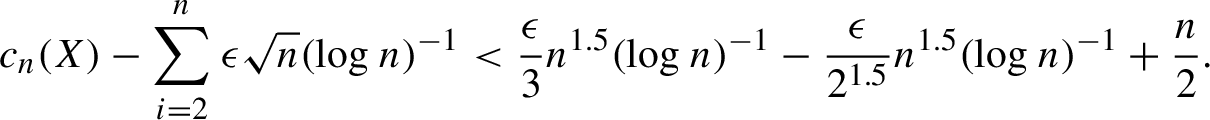 $$ \begin{align*} c_n(X) - \sum_{i = 2}^n \epsilon \sqrt{n} (\log n)^{-1} < \frac{\epsilon}{3} n^{1.5} (\log n)^{-1} - \frac{\epsilon}{2^{1.5}} n^{1.5} (\log n)^{-1} + \frac{n}{2}. \end{align*} $$
$$ \begin{align*} c_n(X) - \sum_{i = 2}^n \epsilon \sqrt{n} (\log n)^{-1} < \frac{\epsilon}{3} n^{1.5} (\log n)^{-1} - \frac{\epsilon}{2^{1.5}} n^{1.5} (\log n)^{-1} + \frac{n}{2}. \end{align*} $$
Since this last term approaches
![]() $-\infty $
, we have verified equation (6). We now apply Lemma 3.3, and see that there exist infinitely many n for which
$-\infty $
, we have verified equation (6). We now apply Lemma 3.3, and see that there exist infinitely many n for which
Rather than using Lemma 3.3 to bound
![]() $c_n(X)$
, we simply recall that by assumption, there exists N so that
$c_n(X)$
, we simply recall that by assumption, there exists N so that
for all
![]() $n>N$
. This clearly implies that
$n>N$
. This clearly implies that
 $c_{1 + c_n(X)}(X) \leq (n^{1.5})^{1.5} = n^{2.25}$
for any
$c_{1 + c_n(X)}(X) \leq (n^{1.5})^{1.5} = n^{2.25}$
for any
![]() $n>N$
. By Corollary 3.1, for any of the infinitely many
$n>N$
. By Corollary 3.1, for any of the infinitely many
![]() $n> N$
satisfying equations (7) and (8),
$n> N$
satisfying equations (7) and (8),
![]() $|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
$|\mathrm {Aut}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
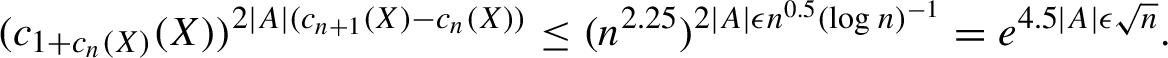 $$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (n^{2.25})^{2|A| \epsilon n^{0.5} (\log n)^{-1}} = e^{4.5 |A| \epsilon \sqrt{n}}. \end{align*} $$
$$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (n^{2.25})^{2|A| \epsilon n^{0.5} (\log n)^{-1}} = e^{4.5 |A| \epsilon \sqrt{n}}. \end{align*} $$
Now, exactly as in the end of Theorem 1.1, any finitely generated subgroup H of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
has growth less than
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
has growth less than
![]() $e^{4.5 |A| \epsilon \sqrt {n}}$
. Since
$e^{4.5 |A| \epsilon \sqrt {n}}$
. Since
![]() $\epsilon> 0$
was arbitrary, by the gap conjecture, H must be virtually nilpotent. Exactly as in the proof of Theorem 1.1, this implies that
$\epsilon> 0$
was arbitrary, by the gap conjecture, H must be virtually nilpotent. Exactly as in the proof of Theorem 1.1, this implies that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is locally finite.
Proof of Theorem 1.4
Choose any subshift X where
![]() ${c_n(X)}/{n^{2} (\log n)^{-1}} \rightarrow 0$
, and any
${c_n(X)}/{n^{2} (\log n)^{-1}} \rightarrow 0$
, and any
![]() $\epsilon> 0$
. We claim that
$\epsilon> 0$
. We claim that
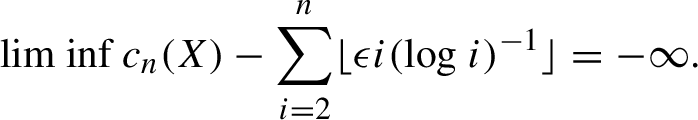 $$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i (\log i)^{-1} \rfloor = -\infty. \end{align} $$
$$ \begin{align} \liminf c_n(X) - \sum_{i = 2}^n \lfloor \epsilon i (\log i)^{-1} \rfloor = -\infty. \end{align} $$
Again, by assumption, there are infinitely many n where
![]() $c_n(X) < ({\epsilon }/{5}) n^2 (\log n)^{-1}$
. Also,
$c_n(X) < ({\epsilon }/{5}) n^2 (\log n)^{-1}$
. Also,
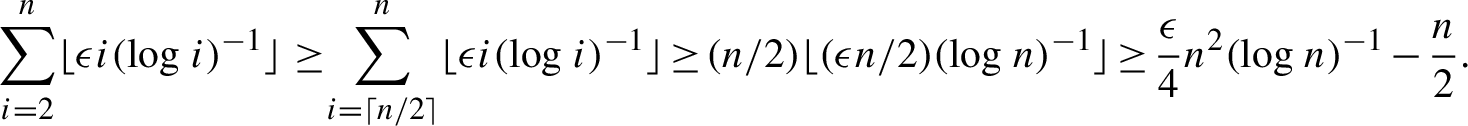 $$ \begin{align*} \sum_{i = 2}^n \lfloor \epsilon i (\log i)^{-1} \rfloor \geq \!\sum_{i = \lceil n/2 \rceil}^n \lfloor \epsilon i (\log i)^{-1} \rfloor \kern1.2pt{\geq}\kern1.2pt (n/2) \lfloor (\epsilon n/2) (\log n)^{-1} \rfloor \kern1.2pt{\geq}\kern1.2pt \frac{\epsilon}{4} n^2 (\log n)^{-1} \kern1.2pt{-}\kern1.2pt \frac{n}{2}. \end{align*} $$
$$ \begin{align*} \sum_{i = 2}^n \lfloor \epsilon i (\log i)^{-1} \rfloor \geq \!\sum_{i = \lceil n/2 \rceil}^n \lfloor \epsilon i (\log i)^{-1} \rfloor \kern1.2pt{\geq}\kern1.2pt (n/2) \lfloor (\epsilon n/2) (\log n)^{-1} \rfloor \kern1.2pt{\geq}\kern1.2pt \frac{\epsilon}{4} n^2 (\log n)^{-1} \kern1.2pt{-}\kern1.2pt \frac{n}{2}. \end{align*} $$
So, for infinitely many n,
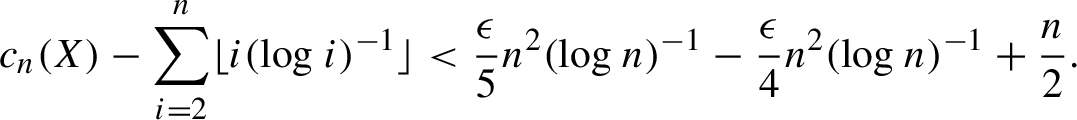 $$ \begin{align*} c_n(X) - \sum_{i = 2}^n \lfloor i (\log i)^{-1} \rfloor < \frac{\epsilon}{5} n^2 (\log n)^{-1} - \frac{\epsilon}{4} n^2 (\log n)^{-1} +\frac{n}{2}. \end{align*} $$
$$ \begin{align*} c_n(X) - \sum_{i = 2}^n \lfloor i (\log i)^{-1} \rfloor < \frac{\epsilon}{5} n^2 (\log n)^{-1} - \frac{\epsilon}{4} n^2 (\log n)^{-1} +\frac{n}{2}. \end{align*} $$
Since this last term approaches
![]() $-\infty $
, we have verified equation (9). We now apply Lemma 3.3, and see that there exist infinitely many n for which
$-\infty $
, we have verified equation (9). We now apply Lemma 3.3, and see that there exist infinitely many n for which
Rather than using Lemma 3.3 to bound
![]() $c_n(X)$
, we simply recall that by assumption, there exists N so that
$c_n(X)$
, we simply recall that by assumption, there exists N so that
for all
![]() $n>N$
. This clearly implies that
$n>N$
. This clearly implies that
 $c_{1 + c_n(X)}(X) \leq (n^{2})^{2} = n^{4}$
for any
$c_{1 + c_n(X)}(X) \leq (n^{2})^{2} = n^{4}$
for any
![]() $n>N$
. Now, by Theorem 3.2, for any of the infinitely many
$n>N$
. Now, by Theorem 3.2, for any of the infinitely many
![]() $n> N$
satisfying equations (10) and (11),
$n> N$
satisfying equations (10) and (11),
 $|\mathrm {Aut}^{(\textit{FIP})}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
$|\mathrm {Aut}^{(\textit{FIP})}_{\lfloor (n-1)/2 \rfloor }(X, \sigma )|$
is bounded from above by
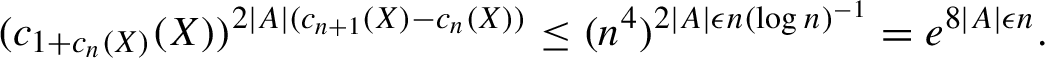 $$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (n^{4})^{2|A| \epsilon n (\log n)^{-1}} = e^{8 |A| \epsilon n}. \end{align*} $$
$$ \begin{align*} (c_{1+c_n(X)}(X))^{2|A| (c_{n+1}(X) - c_n(X))} \leq (n^{4})^{2|A| \epsilon n (\log n)^{-1}} = e^{8 |A| \epsilon n}. \end{align*} $$
By compactness, the set of isolated periodic points of X is finite; denote this set by
![]() $\mathcal {P}$
. It is straightforward to check that the set
$\mathcal {P}$
. It is straightforward to check that the set
![]() $\mathcal {P}$
is invariant under any automorphism of
$\mathcal {P}$
is invariant under any automorphism of
![]() $(X,\sigma )$
, and we may consider the homomorphism
$(X,\sigma )$
, and we may consider the homomorphism
 $$ \begin{align*} \begin{gathered} \pi_{\mathcal{P}} \colon \mathrm{Aut}(X,\sigma) \to \textrm{Aut}(\mathcal{P},\sigma|_{\mathcal{P}})\\ \pi_{\mathcal{P}} \colon \phi \mapsto \phi|_{\mathcal{P}}. \end{gathered} \end{align*} $$
$$ \begin{align*} \begin{gathered} \pi_{\mathcal{P}} \colon \mathrm{Aut}(X,\sigma) \to \textrm{Aut}(\mathcal{P},\sigma|_{\mathcal{P}})\\ \pi_{\mathcal{P}} \colon \phi \mapsto \phi|_{\mathcal{P}}. \end{gathered} \end{align*} $$
By definition, we have
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma ) = \mathrm {ker}(\pi _{\mathcal {P}})$
. Now, exactly as in the end of Theorem 1.1, any finitely generated subgroup H of
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma ) = \mathrm {ker}(\pi _{\mathcal {P}})$
. Now, exactly as in the end of Theorem 1.1, any finitely generated subgroup H of
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
has growth less than
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
has growth less than
![]() $e^{8 |A| \epsilon n}$
. Since
$e^{8 |A| \epsilon n}$
. Since
![]() $\epsilon $
was arbitrary, this implies that H has subexponential growth, and so is amenable. Then, every finitely generated subgroup of
$\epsilon $
was arbitrary, this implies that H has subexponential growth, and so is amenable. Then, every finitely generated subgroup of
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is amenable, implying that
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is amenable, implying that
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is amenable. Since
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is amenable. Since
![]() $\mathcal {P}$
is finite,
$\mathcal {P}$
is finite,
![]() $\mathrm {Aut}(\mathcal {P},\sigma |_{\mathcal {P}})$
is a finite group, and hence
$\mathrm {Aut}(\mathcal {P},\sigma |_{\mathcal {P}})$
is a finite group, and hence
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is of finite index in
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is of finite index in
![]() $\mathrm {Aut}(X,\sigma )$
. Since
$\mathrm {Aut}(X,\sigma )$
. Since
![]() $\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is amenable, this implies
$\mathrm {Aut}^{(\textit{FIP})}(X, \sigma )$
is amenable, this implies
![]() $\mathrm {Aut}(X,\sigma )$
is amenable.
$\mathrm {Aut}(X,\sigma )$
is amenable.
4 Realizing locally finite groups as
 ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
for low complexity
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
for low complexity
In this section, we prove Theorem 1.5. We first outline the general block concatenation construction of subshifts; for an introduction, see [Reference Hahn and Katznelson12, Reference Petersen14]. It is simple to guarantee that such a subshift be minimal. The difficult part will be to engineer our subshift to have low complexity and prescribed
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
.
A block concatenation subshift is defined by an alphabet
![]() $\mathcal {A}$
, sequences
$\mathcal {A}$
, sequences
![]() $(n_k)$
of positive integers, and sets
$(n_k)$
of positive integers, and sets
![]() $A_k \subset \mathcal {A}^{n_k}$
with the following property: for every k, every
$A_k \subset \mathcal {A}^{n_k}$
with the following property: for every k, every
![]() $w \in A_{k+1}$
is a concatenation of
$w \in A_{k+1}$
is a concatenation of
![]() $A_k$
-words. (This of course implies that
$A_k$
-words. (This of course implies that
![]() $n_k$
divides
$n_k$
divides
![]() $n_{k+1}$
for all k.) We will always take
$n_{k+1}$
for all k.) We will always take
![]() $n_1 = 1$
and
$n_1 = 1$
and
![]() $A_1 = \mathcal {A}$
. Given such
$A_1 = \mathcal {A}$
. Given such
![]() $\mathcal {A}$
,
$\mathcal {A}$
,
![]() $(n_k)$
, and
$(n_k)$
, and
![]() $(A_k)$
, X consists of all ‘limits’ of
$(A_k)$
, X consists of all ‘limits’ of
![]() $A_k$
-words (as
$A_k$
-words (as
![]() $k \rightarrow \infty $
); more formally,
$k \rightarrow \infty $
); more formally,
![]() $x \in X$
if and only if for all n, there exists k so that
$x \in X$
if and only if for all n, there exists k so that
![]() $x([-n,n])$
is a subword of some
$x([-n,n])$
is a subword of some
![]() $A_k$
-word.
$A_k$
-word.
We first prove some general lemmas about block concatenation subshifts. The following is well known [Reference Hahn and Katznelson12], but we will give a short proof for completeness.
Lemma 4.1. If every
![]() $A_{k+1}$
-word, written as a concatenation of
$A_{k+1}$
-word, written as a concatenation of
![]() $A_k$
-words, contains each
$A_k$
-words, contains each
![]() $A_k$
-word at least once, then X is minimal.
$A_k$
-word at least once, then X is minimal.
Proof. For every
![]() $w \in L(X)$
, there exists k so that w is a subword of some
$w \in L(X)$
, there exists k so that w is a subword of some
![]() $A_k$
-word. However, then w is a subword of every
$A_k$
-word. However, then w is a subword of every
![]() $A_{k+1}$
-word. For every
$A_{k+1}$
-word. For every
![]() $x \in X$
, x contains an
$x \in X$
, x contains an
![]() $A_{k+1}$
-word, so contains w. Since x and w were arbitrary, X is minimal.
$A_{k+1}$
-word, so contains w. Since x and w were arbitrary, X is minimal.
By definition, for every
![]() $x \in X$
and
$x \in X$
and
![]() $k \in \mathbb {N}$
, x can be written as a bi-infinite concatenation of
$k \in \mathbb {N}$
, x can be written as a bi-infinite concatenation of
![]() $A_k$
-words. We say that X is uniquely decomposable if this decomposition is unique for all
$A_k$
-words. We say that X is uniquely decomposable if this decomposition is unique for all
![]() $x \in X$
. This can also be achieved through a simple assumption about repetitions of
$x \in X$
. This can also be achieved through a simple assumption about repetitions of
![]() $A_k$
-words.
$A_k$
-words.
Lemma 4.2. If
![]() $(d_k)$
is an integer sequence where each
$(d_k)$
is an integer sequence where each
![]() $A_{k+1}$
-word, written as a concatenation of
$A_{k+1}$
-word, written as a concatenation of
![]() $A_k$
-words, begins with
$A_k$
-words, begins with
![]() $d_{k+1}$
repetitions of the same
$d_{k+1}$
repetitions of the same
![]() $A_k$
-word, ends with
$A_k$
-word, ends with
![]() $d_{k+1}$
repetitions of the same
$d_{k+1}$
repetitions of the same
![]() $A_k$
-word, and does not elsewhere contain
$A_k$
-word, and does not elsewhere contain
![]() $d_{k+1}$
repetitions of the same
$d_{k+1}$
repetitions of the same
![]() $A_k$
-word, then X is uniquely decomposable.
$A_k$
-word, then X is uniquely decomposable.
Proof. We prove by induction on k. The base case
![]() $k = 1$
simply says that locations of
$k = 1$
simply says that locations of
![]() $A_1$
-words are uniquely determined for such subshifts, which is trivial since we always take
$A_1$
-words are uniquely determined for such subshifts, which is trivial since we always take
![]() $A_1$
to be the alphabet
$A_1$
to be the alphabet
![]() $\mathcal {A}$
. For the inductive step, assume for some k that for every
$\mathcal {A}$
. For the inductive step, assume for some k that for every
![]() $x \in X$
, x can be uniquely decomposed into
$x \in X$
, x can be uniquely decomposed into
![]() $A_k$
-words. Given this decomposition, one simply searches for
$A_k$
-words. Given this decomposition, one simply searches for
![]() $2d_{k+1}$
-fold concatenations of the form
$2d_{k+1}$
-fold concatenations of the form
![]() $v^{d_{k+1}} w^{d_{k+1}}$
(with
$v^{d_{k+1}} w^{d_{k+1}}$
(with
![]() $v,w \in A_k$
possibly equal), which can only occur with
$v,w \in A_k$
possibly equal), which can only occur with
![]() $v^{d_{k+1}}$
at the end of one
$v^{d_{k+1}}$
at the end of one
![]() $A_{k+1}$
-word and
$A_{k+1}$
-word and
![]() $w^{d_{k+1}}$
at the beginning of another. This implies that x can be written in a unique way as a concatenation of
$w^{d_{k+1}}$
at the beginning of another. This implies that x can be written in a unique way as a concatenation of
![]() $A_{k+1}$
-words, completing the inductive step and the proof.
$A_{k+1}$
-words, completing the inductive step and the proof.
Suppose X is uniquely decomposable, let
![]() $k \in \mathbb {N}$
, and let
$k \in \mathbb {N}$
, and let
![]() $\tau \colon A_{k} \to A_{k}$
be a permutation of the
$\tau \colon A_{k} \to A_{k}$
be a permutation of the
![]() $A_{k}$
-words. Associated with
$A_{k}$
-words. Associated with
![]() $\tau $
is a continuous shift-commuting map
$\tau $
is a continuous shift-commuting map
![]() $\alpha _{\tau } \colon X \to (\mathcal {A}^{\mathbb {Z}},\sigma )$
defined as follows: given
$\alpha _{\tau } \colon X \to (\mathcal {A}^{\mathbb {Z}},\sigma )$
defined as follows: given
![]() $x \in X$
, decompose x as a concatenation of
$x \in X$
, decompose x as a concatenation of
![]() $A_{k}$
-words, and apply
$A_{k}$
-words, and apply
![]() $\tau $
to each
$\tau $
to each
![]() $A_{k}$
-word appearing in X. (Note that this map is only well defined because
$A_{k}$
-word appearing in X. (Note that this map is only well defined because
![]() $(X, \sigma )$
was assumed uniquely decomposable; shift-commuting and continuity are then nearly immediate from the definition.) Written symbolically, if we have
$(X, \sigma )$
was assumed uniquely decomposable; shift-commuting and continuity are then nearly immediate from the definition.) Written symbolically, if we have
then
Note that depending on
![]() $\tau $
,
$\tau $
,
![]() $\alpha _{\tau }$
may or may not map X back into X; if it does, then
$\alpha _{\tau }$
may or may not map X back into X; if it does, then
![]() $\alpha _{\tau }$
is an automorphism of
$\alpha _{\tau }$
is an automorphism of
![]() $(X,\sigma )$
.
$(X,\sigma )$
.
We are now prepared to define the block concatenation subshifts which will prove Theorem 1.5.
Proof of Theorem 1.5
Choose any unbounded increasing f and countable locally finite group G; G can be written, by definition, as the union of an increasing chain of finite subgroups, that is there exist finite groups
![]() $H_k$
so that
$H_k$
so that
![]() $H_k$
is a proper subgroup of
$H_k$
is a proper subgroup of
![]() $H_{k+1}$
for all n, and G is the union of the
$H_{k+1}$
for all n, and G is the union of the
![]() $H_k$
. Choose an increasing sequence
$H_k$
. Choose an increasing sequence
![]() $(b_k)$
of integers greater than
$(b_k)$
of integers greater than
![]() $1$
with the property that
$1$
with the property that
 $f(b_k)> k(|H_k|^{5|H_{k+1}| + 2|H_k|^2})$
for all k.
$f(b_k)> k(|H_k|^{5|H_{k+1}| + 2|H_k|^2})$
for all k.
Our technique is somewhat similar to that of [Reference Boyle, Lind and Rudolph2], where a subshift X was constructed for which the additive group of rationals embeds into
![]() $\mathrm {Aut}(X,\sigma )$
, in that we will construct, for every k, automorphisms defined by their action on the set
$\mathrm {Aut}(X,\sigma )$
, in that we will construct, for every k, automorphisms defined by their action on the set
![]() $A_k$
, and then show that every automorphism of X can be realized in this way. Specifically, for each k, we will define a group of permutations of the words in
$A_k$
, and then show that every automorphism of X can be realized in this way. Specifically, for each k, we will define a group of permutations of the words in
![]() $A_k$
which is isomorphic to
$A_k$
which is isomorphic to
![]() $H_k$
. We will then show that for any k, each
$H_k$
. We will then show that for any k, each
![]() $A_k$
-permutation induces an
$A_k$
-permutation induces an
![]() $A_{k+1}$
-permutation by coordinatewise application to
$A_{k+1}$
-permutation by coordinatewise application to
![]() $A_k$
-words, in a manner that is compatible with the containment of
$A_k$
-words, in a manner that is compatible with the containment of
![]() $H_k$
as a subgroup of
$H_k$
as a subgroup of
![]() $H_{k+1}$
.
$H_{k+1}$
.
We begin with some notation. For every k, fix an ordering
 $(h_1^{(k)}, \ldots , h_{|H_k|}^{(k)})$
of the elements of
$(h_1^{(k)}, \ldots , h_{|H_k|}^{(k)})$
of the elements of
![]() $H_k$
, where
$H_k$
, where
 $h_1^{(k)} = \{\mathrm {id}\}$
. Write
$h_1^{(k)} = \{\mathrm {id}\}$
. Write
![]() $q_k = |H_k|/|H_{k-1}|$
, and choose any set
$q_k = |H_k|/|H_{k-1}|$
, and choose any set
 $\{r_i^{(k)}\}_{i = 1}^{q_k}$
of representatives for right cosets of
$\{r_i^{(k)}\}_{i = 1}^{q_k}$
of representatives for right cosets of
![]() $H_{k-1}$
in
$H_{k-1}$
in
![]() $H_{k}$
, that is
$H_{k}$
, that is
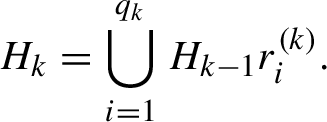 $$ \begin{align*} H_{k} = \bigcup_{i=1}^{q_k} H_{k-1} r_i^{(k)}. \end{align*} $$
$$ \begin{align*} H_{k} = \bigcup_{i=1}^{q_k} H_{k-1} r_i^{(k)}. \end{align*} $$
Without loss of generality, we will always take
 $r_1^{(k)} = \{\mathrm {id}\}$
, the identity element of G (and of all
$r_1^{(k)} = \{\mathrm {id}\}$
, the identity element of G (and of all
![]() $H_k$
). We will now recursively define the sets
$H_k$
). We will now recursively define the sets
![]() $A_k$
and lengths
$A_k$
and lengths
![]() $n_k$
. In our construction,
$n_k$
. In our construction,
![]() $|A_k| = |H_k|$
for every k.
$|A_k| = |H_k|$
for every k.
The
![]() $k = 1$
case is simple; for every
$k = 1$
case is simple; for every
![]() $g \in H_1$
, define a symbol
$g \in H_1$
, define a symbol
 $w_g^{(1)}$
, and define the alphabet
$w_g^{(1)}$
, and define the alphabet
 $A_1 = \{w_g^{(1)} : g \in H_1\}$
; clearly
$A_1 = \{w_g^{(1)} : g \in H_1\}$
; clearly
![]() $|A_1| = |H_1|$
.
$|A_1| = |H_1|$
.
We now define
![]() $A_{k+1}$
for
$A_{k+1}$
for
![]() $k \geq 1$
, assuming that
$k \geq 1$
, assuming that
 $A_k = \{w_g^{(k)} : g \in H_k\}$
has been defined already. Informally, the idea is that we will define
$A_k = \{w_g^{(k)} : g \in H_k\}$
has been defined already. Informally, the idea is that we will define
 $w_g^{(k+1)}$
for every
$w_g^{(k+1)}$
for every
![]() $g \in H_{k+1}$
by assigning a different ‘template’ concatenation of
$g \in H_{k+1}$
by assigning a different ‘template’ concatenation of
![]() $A_k$
-words to each coset representative
$A_k$
-words to each coset representative
 $r_i^{(k+1)}$
, and then permuting the
$r_i^{(k+1)}$
, and then permuting the
![]() $A_k$
-words
$A_k$
-words
 $\{w_g^{(k)}\}_{g \in H_k}$
in those templates by multiplying on the left by a properly chosen
$\{w_g^{(k)}\}_{g \in H_k}$
in those templates by multiplying on the left by a properly chosen
![]() $g'$
in the subscripts.
$g'$
in the subscripts.
More formally, for every
![]() $g \in H_{k+1}$
, we first write
$g \in H_{k+1}$
, we first write
 $g = g' r_i^{(k+1)}$
for some
$g = g' r_i^{(k+1)}$
for some
![]() $g' \in H_k$
and
$g' \in H_k$
and
![]() $1 \leq i \leq q_{k+1}$
. We then define
$1 \leq i \leq q_{k+1}$
. We then define
 $$ \begin{align*} w_{g}^{(k+1)} = w_{g' r_i^{(k+1)}}^{(k+1)} &= \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{2b_{k+1} q_{k+1}}\\ &\ \, \quad\Big( \Big(w_{g' h_1^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big| \cdots \Big| \Big(w_{g' h_{|H_k|-1}^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_{|H_k|}^{(1)}}^{(1)}\Big)^{b_{k+1}}\Big)\\ &\ \, \quad\Big(w_{g' h_{1}^{(k)}}^{(k)}\Big)^{ib_{k+1}} \Big(w_{g' h_{2}^{(k)}}^{(k)}\Big)^{b_{k+1}(3q_{k+1}-i)}. \end{align*} $$
$$ \begin{align*} w_{g}^{(k+1)} = w_{g' r_i^{(k+1)}}^{(k+1)} &= \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{2b_{k+1} q_{k+1}}\\ &\ \, \quad\Big( \Big(w_{g' h_1^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big| \cdots \Big| \Big(w_{g' h_{|H_k|-1}^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_{|H_k|}^{(1)}}^{(1)}\Big)^{b_{k+1}}\Big)\\ &\ \, \quad\Big(w_{g' h_{1}^{(k)}}^{(k)}\Big)^{ib_{k+1}} \Big(w_{g' h_{2}^{(k)}}^{(k)}\Big)^{b_{k+1}(3q_{k+1}-i)}. \end{align*} $$
Here, the concatenation inside the largest parentheses is a list of all pairs of the form
 $\Big (w_{g' h_a^{(k)}}^{(k)}\Big )^{b_{k+1}} \Big (w_{g' h_b^{(k)}}^{(k)}\Big )^{b_{k+1}}$
, with pairs
$\Big (w_{g' h_a^{(k)}}^{(k)}\Big )^{b_{k+1}} \Big (w_{g' h_b^{(k)}}^{(k)}\Big )^{b_{k+1}}$
, with pairs
![]() $(a,b)$
listed in lexicographic order. We then define
$(a,b)$
listed in lexicographic order. We then define
 $A_{k+1} = \{w_g^{(k+1)} : g \in H_{k+1}\}$
, and note that all
$A_{k+1} = \{w_g^{(k+1)} : g \in H_{k+1}\}$
, and note that all
![]() $A_{k+1}$
-words begin and end with
$A_{k+1}$
-words begin and end with
![]() $2b_{k+1} q_{k+1}$
-fold repetitions of an
$2b_{k+1} q_{k+1}$
-fold repetitions of an
![]() $A_k$
-word. We also note that every
$A_k$
-word. We also note that every
![]() $A_{k+1}$
-word contains no other such repetitions. To see this, note that in the central line of the definition of
$A_{k+1}$
-word contains no other such repetitions. To see this, note that in the central line of the definition of
 $w_g^{(k+1)}$
, no
$w_g^{(k+1)}$
, no
 $\Big (w_{g' h_i^{(k)}}^{(k)}\Big )^{b_{k+1}}$
can repeat four times, since the pair
$\Big (w_{g' h_i^{(k)}}^{(k)}\Big )^{b_{k+1}}$
can repeat four times, since the pair
![]() $(i, i)$
is used only once and it is not possible to have consecutive lexicographic pairs of the form
$(i, i)$
is used only once and it is not possible to have consecutive lexicographic pairs of the form
![]() $(j, i) (i, i) (i, k)$
. Therefore, the largest number of times that an
$(j, i) (i, i) (i, k)$
. Therefore, the largest number of times that an
![]() $A_k$
-word can consecutively repeat aside from the beginning and end of
$A_k$
-word can consecutively repeat aside from the beginning and end of
 $w_g^{(k+1)}$
is
$w_g^{(k+1)}$
is
![]() $\max (3b_{k+1}, ib_{k+1}) < 2b_{k+1} q_{k+1}$
. The length of all
$\max (3b_{k+1}, ib_{k+1}) < 2b_{k+1} q_{k+1}$
. The length of all
![]() $A_{k+1}$
-words is
$A_{k+1}$
-words is
Recursively, this defines
![]() $n_k$
and
$n_k$
and
![]() $A_k$
for all k, and so an associated block concatenation subshift X. We here note a few properties of X which will be useful later.
$A_k$
for all k, and so an associated block concatenation subshift X. We here note a few properties of X which will be useful later.
-
• X is minimal by Lemma 4.1.
-
• X is uniquely decomposable by Lemma 4.2 (with
 $d_k = 2b_k q_k$
).
$d_k = 2b_k q_k$
). -
• Concatenations of the form
 $uvw$
with
$uvw$
with
 $u,v,w \in A_k$
,
$u,v,w \in A_k$
,
 $u \neq v$
, and
$u \neq v$
, and
 $v \neq w$
never appear in points of X, and that every other concatenation
$v \neq w$
never appear in points of X, and that every other concatenation
 $uvw$
with
$uvw$
with
 $u = v$
or
$u = v$
or
 $v = w$
appears within every
$v = w$
appears within every
 $A_{k+1}$
-word.
$A_{k+1}$
-word.
We now wish to bound the complexity of X from above to show that
![]() ${c_n(X)}/{nf(n)} \rightarrow 0$
. Choose any length n; there exists k so that
${c_n(X)}/{nf(n)} \rightarrow 0$
. Choose any length n; there exists k so that
![]() $n_k \leq n < n_{k+1}$
. We first treat the case where n belongs to
$n_k \leq n < n_{k+1}$
. We first treat the case where n belongs to
![]() $[n_k, b_{k+1} n_k)$
. All points of X are concatenations of
$[n_k, b_{k+1} n_k)$
. All points of X are concatenations of
![]() $A_k$
-words, and by definition of
$A_k$
-words, and by definition of
![]() $A_{k+1}$
, each
$A_{k+1}$
, each
![]() $A_k$
-word is repeated some number of times which is a multiple of
$A_k$
-word is repeated some number of times which is a multiple of
![]() $b_{k+1}$
. Therefore, since
$b_{k+1}$
. Therefore, since
![]() $n < b_{k+1} n_k$
, any word
$n < b_{k+1} n_k$
, any word
![]() $w \in L_n(X)$
is of the form
$w \in L_n(X)$
is of the form
![]() $s qq \ldots qq rr \ldots rr p$
, where
$s qq \ldots qq rr \ldots rr p$
, where
![]() $q,r$
are
$q,r$
are
![]() $A_k$
-words, s is a suffix of q, and p is a prefix of r. Then w is determined completely by the location at which the transition from q to r occurs, and the choices of q and r. (The case where w has no transition is still included here by just taking
$A_k$
-words, s is a suffix of q, and p is a prefix of r. Then w is determined completely by the location at which the transition from q to r occurs, and the choices of q and r. (The case where w has no transition is still included here by just taking
![]() $q = r$
.) So,
$q = r$
.) So,
![]() $c_n(X) \leq n |A_k|^2 = n|H_k|^2$
. Since
$c_n(X) \leq n |A_k|^2 = n|H_k|^2$
. Since
![]() $|H_k|^2 < f(b_k)/k < f(n_k)/k$
and
$|H_k|^2 < f(b_k)/k < f(n_k)/k$
and
![]() $n \geq n_k$
, we have
$n \geq n_k$
, we have
![]() $c_n(X) \leq n f(n_k)/k \leq n f(n)/k$
.
$c_n(X) \leq n f(n_k)/k \leq n f(n)/k$
.
Now consider the case where n belongs to
![]() $[b_{k+1} n_k, n_{k+1})$
. Any word
$[b_{k+1} n_k, n_{k+1})$
. Any word
![]() $w \in L_n(X)$
must be of the form
$w \in L_n(X)$
must be of the form
 $s u_1^{b_{k+1}} u_2^{b_{k+1}} \ldots u_{j-1}^{b_{k+1}} p$
, where
$s u_1^{b_{k+1}} u_2^{b_{k+1}} \ldots u_{j-1}^{b_{k+1}} p$
, where
![]() $u_1, \ldots , u_{j-1} \in A_k$
, s is a suffix of some word
$u_1, \ldots , u_{j-1} \in A_k$
, s is a suffix of some word
 $u_0^{b_{k+1}}$
for
$u_0^{b_{k+1}}$
for
![]() $u_0 \in A_k$
, and p is a prefix of some word
$u_0 \in A_k$
, and p is a prefix of some word
 $u_j^{b_{k+1}}$
for
$u_j^{b_{k+1}}$
for
![]() $u_j \in A_k$
. By equation (13),
$u_j \in A_k$
. By equation (13),
![]() ${n_{k+1}}/{b_{k+1} n_k} < 5q_{k+1} + 2|A_k|^2$
, and so
${n_{k+1}}/{b_{k+1} n_k} < 5q_{k+1} + 2|A_k|^2$
, and so
![]() $j < 5|H_{k+1}| + 2|H_k|^2$
. Clearly, w is determined by the words
$j < 5|H_{k+1}| + 2|H_k|^2$
. Clearly, w is determined by the words
![]() $u_0, \ldots , u_j$
and the length of s, so
$u_0, \ldots , u_j$
and the length of s, so
![]() $c_n(X) \leq b_{k+1} n_k |A_k|^{j+1} = b_{k+1} n_k |H_k|^{j+1}$
. Since
$c_n(X) \leq b_{k+1} n_k |A_k|^{j+1} = b_{k+1} n_k |H_k|^{j+1}$
. Since
![]() $j < 5|H_{k+1}| + 2|H_k|^2$
,
$j < 5|H_{k+1}| + 2|H_k|^2$
,
 $$ \begin{align*} |H_k|^{j+1} \leq |H_k|^{5|H_{k+1}| + 2|H_k|^2} < f(b_{k})/k < f(b_{k+1} n_k)/k. \end{align*} $$
$$ \begin{align*} |H_k|^{j+1} \leq |H_k|^{5|H_{k+1}| + 2|H_k|^2} < f(b_{k})/k < f(b_{k+1} n_k)/k. \end{align*} $$
Since
![]() $n \geq b_{k+1} n_k$
, this implies that
$n \geq b_{k+1} n_k$
, this implies that
![]() $c_n(X) \leq n f(b_{k+1} n_k)/k \leq n f(n)/k$
.
$c_n(X) \leq n f(b_{k+1} n_k)/k \leq n f(n)/k$
.
We have shown that for all
![]() $n \geq n_k$
,
$n \geq n_k$
,
![]() $c_n(X) \leq nf(n)/k$
, and so
$c_n(X) \leq nf(n)/k$
, and so
![]() ${c_n(X)}/{nf(n)} \rightarrow 0$
. It remains only to show that
${c_n(X)}/{nf(n)} \rightarrow 0$
. It remains only to show that
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is isomorphic to G.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is isomorphic to G.
For any k and
![]() $h \in H_k$
, define the permutation
$h \in H_k$
, define the permutation
![]() $\pi _{k,h}$
of the set
$\pi _{k,h}$
of the set
 $\{w_g^{(k)}\}$
of
$\{w_g^{(k)}\}$
of
![]() $A_k$
-words by left multiplication of the subscript, that is
$A_k$
-words by left multiplication of the subscript, that is
 $\pi _{k,h}(w_g^{(k)}) = w_{hg}^{(k)}$
. In a slight abuse of notation, we also define
$\pi _{k,h}(w_g^{(k)}) = w_{hg}^{(k)}$
. In a slight abuse of notation, we also define
![]() $\pi _{k,h}$
to act on concatenations of
$\pi _{k,h}$
to act on concatenations of
![]() $A_k$
-words by ‘coordinatewise’ application, that is if
$A_k$
-words by ‘coordinatewise’ application, that is if
![]() $w_1, \ldots , w_m \in A_k$
,
$w_1, \ldots , w_m \in A_k$
,
![]() $\pi _{k,h}(w_1 \ldots w_m) := \pi _{k,h}(w_1) \ldots \pi _{k,h}(w_m)$
. (We note that this definition is well defined because X is uniquely decomposable.)
$\pi _{k,h}(w_1 \ldots w_m) := \pi _{k,h}(w_1) \ldots \pi _{k,h}(w_m)$
. (We note that this definition is well defined because X is uniquely decomposable.)
Lemma 4.3. For any
![]() $k \ge 1$
,
$k \ge 1$
,
![]() $h \in H_k$
, and
$h \in H_k$
, and
![]() $w \in A_{k+1}$
,
$w \in A_{k+1}$
,
![]() $\pi _{k,h}(w) = \pi _{k+1,h}(w)$
.
$\pi _{k,h}(w) = \pi _{k+1,h}(w)$
.
Proof. This comes from the definition of
![]() $A_{k+1}$
. Informally, it is due to the fact that a left multiplication by any
$A_{k+1}$
. Informally, it is due to the fact that a left multiplication by any
![]() $h \in H_k$
in the subscript of an
$h \in H_k$
in the subscript of an
![]() $A_{k+1}$
-word
$A_{k+1}$
-word
 $w_{g' r_i^{(k+1)}}^{(k+1)}$
passes through to left multiplications of all subscripts of the component
$w_{g' r_i^{(k+1)}}^{(k+1)}$
passes through to left multiplications of all subscripts of the component
![]() $A_k$
-words.
$A_k$
-words.
More formally, choose any
![]() $k \ge 1$
,
$k \ge 1$
,
![]() $h \in H_k$
and
$h \in H_k$
and
![]() $g \in H_{k+1}$
; we can write
$g \in H_{k+1}$
; we can write
 $g = g' r_i^{(k+1)}$
for some
$g = g' r_i^{(k+1)}$
for some
![]() $g^{\prime } \in H_k$
and
$g^{\prime } \in H_k$
and
![]() $1 \leq i \leq q_{k+1}$
. Then,
$1 \leq i \leq q_{k+1}$
. Then,
 $$ \begin{align*} \pi_{k,h}\Big(w_{g}^{(k+1)}\Big) &= \pi_{k,h}\Big(w_{g' r_i^{(k+1)}}^{(k+1)}\Big)\\& = \pi_{k,h}\Big( \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{2b_{k+1} q_{k+1}}\\ &\quad\Big( \Big(w_{g' h_1^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big| \cdots \Big| \Big(w_{g' h_{s_k-1}^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_{s_k}^{(1)}}^{(1)}\Big)^{b_{k+1}}\Big)\\ &\quad\Big(w_{g' h_{1}^{(k)}}^{(k)}\Big)^{ib_{k+1}} \Big(w_{g' h_{2}^{(k)}}^{(k)}\Big)^{b_{k+1}(3q_{k+1}-i)} \Big)\\ &= \Big(w_{hg' h_2^{(k)}}^{(k)}\Big)^{2b_{k+1} q_{k+1}}\\ &\quad\Big( \Big(w_{hg' h_1^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{hg' h_2^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big| \cdots \Big| \Big(w_{hg' h_{s_k-1}^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{hg' h_{s_k}^{(1)}}^{(1)}\Big)^{b_{k+1}}\Big)\\ &\quad\Big(w_{hg' h_{1}^{(k)}}^{(k)}\Big)^{ib_{k+1}} \Big(w_{hg' h_{2}^{(k)}}^{(k)}\Big)^{b_{k+1}(3q_{k+1}-i)}\\ &= w_{hg' r_i^{(k+1)}}^{(k+1)} = \pi_{k+1,h}\Big(w_{g' r_i^{(k+1)}}^{(k+1)}\Big) = \pi_{k+1,h}\Big(w_{g}^{(k+1)}\Big).\\[-42pt] \end{align*} $$
$$ \begin{align*} \pi_{k,h}\Big(w_{g}^{(k+1)}\Big) &= \pi_{k,h}\Big(w_{g' r_i^{(k+1)}}^{(k+1)}\Big)\\& = \pi_{k,h}\Big( \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{2b_{k+1} q_{k+1}}\\ &\quad\Big( \Big(w_{g' h_1^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_2^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big| \cdots \Big| \Big(w_{g' h_{s_k-1}^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{g' h_{s_k}^{(1)}}^{(1)}\Big)^{b_{k+1}}\Big)\\ &\quad\Big(w_{g' h_{1}^{(k)}}^{(k)}\Big)^{ib_{k+1}} \Big(w_{g' h_{2}^{(k)}}^{(k)}\Big)^{b_{k+1}(3q_{k+1}-i)} \Big)\\ &= \Big(w_{hg' h_2^{(k)}}^{(k)}\Big)^{2b_{k+1} q_{k+1}}\\ &\quad\Big( \Big(w_{hg' h_1^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{hg' h_2^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big| \cdots \Big| \Big(w_{hg' h_{s_k-1}^{(k)}}^{(k)}\Big)^{b_{k+1}} \Big(w_{hg' h_{s_k}^{(1)}}^{(1)}\Big)^{b_{k+1}}\Big)\\ &\quad\Big(w_{hg' h_{1}^{(k)}}^{(k)}\Big)^{ib_{k+1}} \Big(w_{hg' h_{2}^{(k)}}^{(k)}\Big)^{b_{k+1}(3q_{k+1}-i)}\\ &= w_{hg' r_i^{(k+1)}}^{(k+1)} = \pi_{k+1,h}\Big(w_{g' r_i^{(k+1)}}^{(k+1)}\Big) = \pi_{k+1,h}\Big(w_{g}^{(k+1)}\Big).\\[-42pt] \end{align*} $$
In particular, by induction, Lemma 4.3 implies that for any
![]() $k < m$
,
$k < m$
,
![]() $\pi _{k,h}$
induces the permutation
$\pi _{k,h}$
induces the permutation
![]() $\pi _{m,h}$
of
$\pi _{m,h}$
of
![]() $A_m$
-words by coordinatewise action. By passing to limits, we see that in fact
$A_m$
-words by coordinatewise action. By passing to limits, we see that in fact
![]() $\pi _{k,h}$
induces a self-bijection of X, which we denote by
$\pi _{k,h}$
induces a self-bijection of X, which we denote by
![]() $\phi _{k,h}$
. Since X is uniquely decomposable,
$\phi _{k,h}$
. Since X is uniquely decomposable,
![]() $\phi _{k,h}$
is continuous and shift-commuting (in fact, it is one of the maps
$\phi _{k,h}$
is continuous and shift-commuting (in fact, it is one of the maps
![]() $\alpha _{\tau }$
defined in equation (12)), and so is in
$\alpha _{\tau }$
defined in equation (12)), and so is in
![]() $\mathrm {Aut}(X, \sigma )$
.
$\mathrm {Aut}(X, \sigma )$
.
For every k, the group
![]() $\{\phi _{k,h}\}_{h \in H_k}$
is clearly isomorphic to
$\{\phi _{k,h}\}_{h \in H_k}$
is clearly isomorphic to
![]() $H_k$
itself (since
$H_k$
itself (since
![]() $\phi _{k,h} \circ \phi _{k,h'} = \phi _{k,hh'}$
). The collection
$\phi _{k,h} \circ \phi _{k,h'} = \phi _{k,hh'}$
). The collection
![]() $\{\phi _{k,h}\}_{k \in \mathbb {N}, h \in H_k}$
then forms a subgroup of
$\{\phi _{k,h}\}_{k \in \mathbb {N}, h \in H_k}$
then forms a subgroup of
![]() $\mathrm {Aut}(X,\sigma )$
, which we denote by
$\mathrm {Aut}(X,\sigma )$
, which we denote by
![]() $G_{\phi }$
, and it follows from the above that
$G_{\phi }$
, and it follows from the above that
![]() $G_{\phi }$
is isomorphic to G. We now claim that even after quotienting out by the subgroup generated by the shift, this is still true.
$G_{\phi }$
is isomorphic to G. We now claim that even after quotienting out by the subgroup generated by the shift, this is still true.
Lemma 4.4. Let
![]() $\rho \colon \mathrm {Aut}(X,\sigma ) \to {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
denote the quotient map. Then
$\rho \colon \mathrm {Aut}(X,\sigma ) \to {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
denote the quotient map. Then
![]() $\rho (G_{\phi })$
is isomorphic to G.
$\rho (G_{\phi })$
is isomorphic to G.
Proof. It is enough to show that
![]() $G_{\phi } \cap \ker \rho = \text{id}$
. Therefore, it is enough to show that if
$G_{\phi } \cap \ker \rho = \text{id}$
. Therefore, it is enough to show that if
![]() $\phi _{k,h}=\sigma ^{m}$
for some
$\phi _{k,h}=\sigma ^{m}$
for some
![]() $k,h,m$
, then
$k,h,m$
, then
![]() $m=0$
. Suppose then that
$m=0$
. Suppose then that
![]() $\sigma ^{m} = \phi _{k,h}$
. Choose
$\sigma ^{m} = \phi _{k,h}$
. Choose
![]() $k' \geq k$
so that
$k' \geq k$
so that
![]() $|m| < n_{k'}$
. Then, by Lemma 4.3,
$|m| < n_{k'}$
. Then, by Lemma 4.3,
![]() $\phi _{k,h} = \phi _{k', h}$
, and hence
$\phi _{k,h} = \phi _{k', h}$
, and hence
![]() $\sigma ^{m} = \phi _{k',h}$
. Finally, we note that for any
$\sigma ^{m} = \phi _{k',h}$
. Finally, we note that for any
![]() $x \in X$
,
$x \in X$
,
![]() $\phi _{k',h}(x)$
has
$\phi _{k',h}(x)$
has
![]() $A_{k'}$
-words in the same locations as x. Since
$A_{k'}$
-words in the same locations as x. Since
![]() $\sigma ^m(x) = \phi _{k',h}(x)$
and
$\sigma ^m(x) = \phi _{k',h}(x)$
and
![]() $|m| < n_{k'}$
, the only way for this to happen is if
$|m| < n_{k'}$
, the only way for this to happen is if
![]() $m=0$
, completing the proof.
$m=0$
, completing the proof.
Finally, we must show that under the quotient map
![]() $\rho \colon \mathrm {Aut}(X,\sigma ) \to {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
, the image of
$\rho \colon \mathrm {Aut}(X,\sigma ) \to {{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
, the image of
![]() $G_{\phi }$
is all of
$G_{\phi }$
is all of
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
; in other words, that every automorphism of X can be written as
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
; in other words, that every automorphism of X can be written as
![]() $\sigma ^j \phi _{k,h}$
for some
$\sigma ^j \phi _{k,h}$
for some
![]() $j \in \mathbb {Z}$
,
$j \in \mathbb {Z}$
,
![]() $k \in \mathbb {N}$
, and
$k \in \mathbb {N}$
, and
![]() $h \in H_k$
.
$h \in H_k$
.
We need a technical definition; we say that
![]() $\phi \in \mathrm {Aut}(X, \sigma )$
preserves locations of
$\phi \in \mathrm {Aut}(X, \sigma )$
preserves locations of
![]() $A_k$
-words if, for all
$A_k$
-words if, for all
![]() $x \in X$
and
$x \in X$
and
![]() $m < n$
, if
$m < n$
, if
![]() $x([m,m+n_k))$
is an
$x([m,m+n_k))$
is an
![]() $A_k$
-word, then
$A_k$
-word, then
![]() $(\phi x)([m,m+n_k))$
is an
$(\phi x)([m,m+n_k))$
is an
![]() $A_k$
-word. (Note that preserving locations of
$A_k$
-word. (Note that preserving locations of
![]() $A_k$
-words clearly implies preserving locations of
$A_k$
-words clearly implies preserving locations of
![]() $A_j$
-words for any
$A_j$
-words for any
![]() $j < k$
.) We say that
$j < k$
.) We say that
![]() $\phi $
simply preserves locations if it preserves locations of
$\phi $
simply preserves locations if it preserves locations of
![]() $A_k$
-words for all k.
$A_k$
-words for all k.
It is clear that for every
![]() $\phi \in \mathrm {Aut}(X,\sigma )$
of range
$\phi \in \mathrm {Aut}(X,\sigma )$
of range
![]() $n_{k}$
and every
$n_{k}$
and every
![]() $x \in X$
, there exists a shift i with
$x \in X$
, there exists a shift i with
![]() $|i| \leq n_k/2$
so that
$|i| \leq n_k/2$
so that
![]() $(\phi \circ \sigma ^i)(x)$
has
$(\phi \circ \sigma ^i)(x)$
has
![]() $A_k$
-words at the same locations as x. In theory though, this is weaker than preserving locations of
$A_k$
-words at the same locations as x. In theory though, this is weaker than preserving locations of
![]() $A_k$
-words, as i could depend on x. For our examples, we can show that this is not possible as long as k is large enough.
$A_k$
-words, as i could depend on x. For our examples, we can show that this is not possible as long as k is large enough.
Lemma 4.5. If
![]() $\phi \in \mathrm {Aut}(X,\sigma )$
has range
$\phi \in \mathrm {Aut}(X,\sigma )$
has range
![]() $n_k$
, and for some
$n_k$
, and for some
![]() $x \in X$
,
$x \in X$
,
![]() $\phi x$
has
$\phi x$
has
![]() $A_k$
-words at the same locations as x, then
$A_k$
-words at the same locations as x, then
![]() $\phi $
preserves locations of
$\phi $
preserves locations of
![]() $A_k$
-words.
$A_k$
-words.
Proof. Choose any k,
![]() $\phi $
with range
$\phi $
with range
![]() $n_k$
and inducing block map
$n_k$
and inducing block map
![]() $\Phi $
,
$\Phi $
,
![]() $x \in X$
, and suppose that
$x \in X$
, and suppose that
![]() $\phi x$
has
$\phi x$
has
![]() $A_k$
-words at the same locations as x. By shifting x, we may assume without loss of generality that
$A_k$
-words at the same locations as x. By shifting x, we may assume without loss of generality that
![]() $x([0, n_{k+1}))$
is an
$x([0, n_{k+1}))$
is an
![]() $A_{k+1}$
-word. Then
$A_{k+1}$
-word. Then
![]() $x([0, n_{k+1}))$
, as an
$x([0, n_{k+1}))$
, as an
![]() $A_{k+1}$
-word, contains all concatenations of three
$A_{k+1}$
-word, contains all concatenations of three
![]() $A_k$
-words which are in
$A_k$
-words which are in
![]() $L(X)$
, that is, for all
$L(X)$
, that is, for all
![]() $u,v,w \in A_{k}$
such that
$u,v,w \in A_{k}$
such that
![]() $uvw \in L(X)$
(that is
$uvw \in L(X)$
(that is
![]() $u=v$
or
$u=v$
or
![]() $v=w$
), there exists
$v=w$
), there exists
![]() $n_k \leq i < n_{k+1} - 2n_k$
so that
$n_k \leq i < n_{k+1} - 2n_k$
so that
![]() $x([i-n_k, i+2n_k)) = uvw$
. This implies that
$x([i-n_k, i+2n_k)) = uvw$
. This implies that
![]() $\Phi (uvw) = (\phi x)([i, i+n_k))$
is an
$\Phi (uvw) = (\phi x)([i, i+n_k))$
is an
![]() $A_k$
-word.
$A_k$
-word.
For any
![]() $y \in X$
and
$y \in X$
and
![]() $j \in \mathbb {Z}$
, if
$j \in \mathbb {Z}$
, if
![]() $y([j, j+n_k)) \in A_k$
, then
$y([j, j+n_k)) \in A_k$
, then
![]() $y([j-n_k, j+2n_k)) = uvw$
for some
$y([j-n_k, j+2n_k)) = uvw$
for some
![]() $u,v,w \in A_k$
, implying that
$u,v,w \in A_k$
, implying that
![]() $(\phi y)([j, j+n_k)) = \Phi (uvw)$
is an
$(\phi y)([j, j+n_k)) = \Phi (uvw)$
is an
![]() $A_k$
-word. Since y was arbitrary,
$A_k$
-word. Since y was arbitrary,
![]() $\phi $
preserves locations of
$\phi $
preserves locations of
![]() $A_k$
-words.
$A_k$
-words.
We now wish to show that all automorphisms of X preserve locations up to a shift.
Lemma 4.6. For every
![]() $\phi \in \mathrm {Aut}(X, \sigma )$
, there exists i so that
$\phi \in \mathrm {Aut}(X, \sigma )$
, there exists i so that
![]() $\sigma ^i \circ \phi $
preserves locations.
$\sigma ^i \circ \phi $
preserves locations.
Proof. Choose any
![]() $\phi \in \mathrm {Aut}(X, \sigma )$
, and choose k so that both
$\phi \in \mathrm {Aut}(X, \sigma )$
, and choose k so that both
![]() $\phi $
and
$\phi $
and
![]() $\phi ^{-1}$
have range
$\phi ^{-1}$
have range
![]() $n_k/2$
. Choose any
$n_k/2$
. Choose any
![]() $x \in X$
with
$x \in X$
with
![]() $x([0, n_{k+1}))$
an
$x([0, n_{k+1}))$
an
![]() $A_{k+1}$
-word. There clearly exists i with
$A_{k+1}$
-word. There clearly exists i with
![]() $|i| < n_k/2$
so that for all m,
$|i| < n_k/2$
so that for all m,
![]() $(\phi \circ \sigma ^i x)([mn_k, (m+1)n_k))$
is an
$(\phi \circ \sigma ^i x)([mn_k, (m+1)n_k))$
is an
![]() $A_k$
-word. Write
$A_k$
-word. Write
![]() $\phi ' := \phi \circ \sigma ^i$
. By additivity of ranges under composition,
$\phi ' := \phi \circ \sigma ^i$
. By additivity of ranges under composition,
![]() $\phi '$
and
$\phi '$
and
![]() $\phi ^{\prime -1}$
have range
$\phi ^{\prime -1}$
have range
![]() $n_k$
, and by Lemma 4.5,
$n_k$
, and by Lemma 4.5,
![]() $\phi '$
preserves locations of
$\phi '$
preserves locations of
![]() $A_k$
-words.
$A_k$
-words.
Now, consider any
![]() $x \in X$
for which
$x \in X$
for which
![]() $x([-n_{k+1}, 0))$
and
$x([-n_{k+1}, 0))$
and
![]() $x([0, n_{k+1}))$
are both
$x([0, n_{k+1}))$
are both
![]() $A_{k+1}$
-words, and
$A_{k+1}$
-words, and
![]() $x([-n_{k+1}, 0))$
ends with the same
$x([-n_{k+1}, 0))$
ends with the same
![]() $2b_{k+1} c_{k+1}$
-fold repetition of an
$2b_{k+1} c_{k+1}$
-fold repetition of an
![]() $A_k$
-word that
$A_k$
-word that
![]() $x([0, n_{k+1}))$
begins with. Then
$x([0, n_{k+1}))$
begins with. Then
![]() $x([-2b_{k+1} c_{k+1} n_k, 2b_{k+1} c_{k+1} n_k)) = w^{4b_{k+1} c_{k+1}}$
for some
$x([-2b_{k+1} c_{k+1} n_k, 2b_{k+1} c_{k+1} n_k)) = w^{4b_{k+1} c_{k+1}}$
for some
![]() $w \in A_k$
. Since
$w \in A_k$
. Since
![]() $\phi $
preserves locations of
$\phi $
preserves locations of
![]() $A_k$
-words and has range less than
$A_k$
-words and has range less than
![]() $n_k$
,
$n_k$
,
![]() $(\phi ' x)([(-2b_{k+1} c_{k+1} + 1)n_k, (2b_{k+1} c_{k+1} - 1)n_k)) = v^{4b_{k+1} c_{k+1} - 2}$
for some
$(\phi ' x)([(-2b_{k+1} c_{k+1} + 1)n_k, (2b_{k+1} c_{k+1} - 1)n_k)) = v^{4b_{k+1} c_{k+1} - 2}$
for some
![]() $v \in A_k$
. However, the only
$v \in A_k$
. However, the only
![]() $(4b_{k+1} c_{k+1} - 2)$
-fold repetitions of
$(4b_{k+1} c_{k+1} - 2)$
-fold repetitions of
![]() $A_k$
-words within points of x are within the
$A_k$
-words within points of x are within the
![]() $(4b_{k+1} c_{k+1})$
-fold repetitions occurring across the boundary of some pairs of
$(4b_{k+1} c_{k+1})$
-fold repetitions occurring across the boundary of some pairs of
![]() $A_{k+1}$
-words. Therefore, there exists some
$A_{k+1}$
-words. Therefore, there exists some
![]() $j \in \{0, \pm n_k\}$
for which
$j \in \{0, \pm n_k\}$
for which
![]() $((\phi ' \circ \sigma ^j) x)([-2b_{k+1} c_{k+1} n_k, 2b_{k+1} c_{k+1} n_k]) = v^{4b_{k+1} c_{k+1}}$
, which implies that
$((\phi ' \circ \sigma ^j) x)([-2b_{k+1} c_{k+1} n_k, 2b_{k+1} c_{k+1} n_k]) = v^{4b_{k+1} c_{k+1}}$
, which implies that
![]() $((\phi ' \circ \sigma ^j) x)([-n_{k+1}, 0))$
and
$((\phi ' \circ \sigma ^j) x)([-n_{k+1}, 0))$
and
![]() $((\phi ' \circ \sigma ^j) x)([0, n_{k+1}))$
are
$((\phi ' \circ \sigma ^j) x)([0, n_{k+1}))$
are
![]() $A_{k+1}$
-words, and so that
$A_{k+1}$
-words, and so that
![]() $(\phi ' \circ \sigma ^j) x$
has
$(\phi ' \circ \sigma ^j) x$
has
![]() $A_{k+1}$
-words in the same locations as x. Define
$A_{k+1}$
-words in the same locations as x. Define
![]() $\phi '' := \phi ' \circ \sigma ^j$
; since
$\phi '' := \phi ' \circ \sigma ^j$
; since
![]() $\phi ', \phi ^{\prime -1}$
had range
$\phi ', \phi ^{\prime -1}$
had range
![]() $n_k$
and
$n_k$
and
![]() $|j| \leq n_k$
,
$|j| \leq n_k$
,
![]() $\phi ''$
and
$\phi ''$
and
![]() $\phi ^{\prime \prime -1}$
have range
$\phi ^{\prime \prime -1}$
have range
![]() $2n_k$
by additivity of ranges under composition. Since
$2n_k$
by additivity of ranges under composition. Since
![]() $2n_k < n_{k+1}$
, Lemma 4.5 implies that
$2n_k < n_{k+1}$
, Lemma 4.5 implies that
![]() $\phi ''$
preserves locations of
$\phi ''$
preserves locations of
![]() $A_{k+1}$
-words. We claim that in fact
$A_{k+1}$
-words. We claim that in fact
![]() $\phi ''$
preserves locations for all
$\phi ''$
preserves locations for all
![]() $A_m$
-words for
$A_m$
-words for
![]() $m> k$
, which will complete the proof since
$m> k$
, which will complete the proof since
![]() $\phi '' = \phi \circ \sigma ^{i+j}$
. We prove by induction on m. The base case
$\phi '' = \phi \circ \sigma ^{i+j}$
. We prove by induction on m. The base case
![]() $m = k+1$
is completed, so we assume that
$m = k+1$
is completed, so we assume that
![]() $m> k$
and that
$m> k$
and that
![]() $\phi ''$
preserves locations of
$\phi ''$
preserves locations of
![]() $A_m$
-words.
$A_m$
-words.
Choose two
![]() $A_{m}$
-words
$A_{m}$
-words
![]() $y, z$
which are not equal, but agree on their first and last
$y, z$
which are not equal, but agree on their first and last
![]() $2n_m$
letters (for instance,
$2n_m$
letters (for instance,
 $w_{\mathrm {id}}^{(m)}$
and
$w_{\mathrm {id}}^{(m)}$
and
 $w_{r_2^{(m)}}^{(m)}$
would work). Choose
$w_{r_2^{(m)}}^{(m)}$
would work). Choose
![]() $x \in X$
so that
$x \in X$
so that
![]() $x([-n_{m+1}, 0))$
and
$x([-n_{m+1}, 0))$
and
![]() $x([0, n_{m+1}))$
are both in
$x([0, n_{m+1}))$
are both in
![]() $A_{m+1}$
,
$A_{m+1}$
,
![]() $x([-n_{m+1}, 0))$
ends with
$x([-n_{m+1}, 0))$
ends with
![]() $y^{2b_{m+1} c_{m+1}}$
, and
$y^{2b_{m+1} c_{m+1}}$
, and
![]() $x([0, n_{m+1}))$
begins with
$x([0, n_{m+1}))$
begins with
![]() $z^{2b_{m+1} c_{m+1}}$
.
$z^{2b_{m+1} c_{m+1}}$
.
Since
![]() $\phi ''$
preserves locations of
$\phi ''$
preserves locations of
![]() $A_{m}$
-words, all words
$A_{m}$
-words, all words
![]() $(\phi '' x)([in_{m}, (i+1)n_{m}))$
for
$(\phi '' x)([in_{m}, (i+1)n_{m}))$
for
![]() $-2b_{m+1} c_{m+1} \leq i < 2b_{m+1} c_{m+1}$
are
$-2b_{m+1} c_{m+1} \leq i < 2b_{m+1} c_{m+1}$
are
![]() $A_{m}$
-words. Since
$A_{m}$
-words. Since
![]() $\phi ''$
has range
$\phi ''$
has range
![]() $2n_k$
, each
$2n_k$
, each
![]() $(\phi '' x)([in_{m}, (i+1)n_{m}))$
depends only on
$(\phi '' x)([in_{m}, (i+1)n_{m}))$
depends only on
![]() $x(in_{m} - 2n_k, (i+1)n_{m} + 2n_k))$
. Since y and z agree on their first and last
$x(in_{m} - 2n_k, (i+1)n_{m} + 2n_k))$
. Since y and z agree on their first and last
![]() $2n_m \geq 2n_k$
letters and
$2n_m \geq 2n_k$
letters and
![]() $(\phi '' x)([in_{m}, (i+1)n_{m}))$
is the same for
$(\phi '' x)([in_{m}, (i+1)n_{m}))$
is the same for
![]() $-2b_{m+1} c_{m+1} < i < 0$
(call this
$-2b_{m+1} c_{m+1} < i < 0$
(call this
![]() $A_{m}$
-word a) and for
$A_{m}$
-word a) and for
![]() $0 \leq i < 2b_{m+1} c_{m+1} - 1$
(call this
$0 \leq i < 2b_{m+1} c_{m+1} - 1$
(call this
![]() $A_{m}$
-word b).
$A_{m}$
-word b).
If
![]() $a = b$
, then since
$a = b$
, then since
![]() $\phi ^{\prime \prime -1}$
has range
$\phi ^{\prime \prime -1}$
has range
![]() $2n_k < n_{m}$
, it would have to be the case that
$2n_k < n_{m}$
, it would have to be the case that
![]() $y = z$
(formally, if
$y = z$
(formally, if
![]() $\Psi $
is an inducing block map for
$\Psi $
is an inducing block map for
![]() $\phi ^{\prime \prime -1}$
, then since
$\phi ^{\prime \prime -1}$
, then since
![]() $a = (\phi '' x)([-2n_{m} - 2n_k, -n_{m} + 2n_k) = (\phi '' x)([n_{m} - 2n_k, 2n_{m} + 2n_k) = b$
, it must be the case that
$a = (\phi '' x)([-2n_{m} - 2n_k, -n_{m} + 2n_k) = (\phi '' x)([n_{m} - 2n_k, 2n_{m} + 2n_k) = b$
, it must be the case that
![]() $y = \Psi (a) = x([-2n_{m}, -n_{m}) = x([n_{m}, 2n_{m}) = \Psi (b) = z$
.) This is a contradiction, so
$y = \Psi (a) = x([-2n_{m}, -n_{m}) = x([n_{m}, 2n_{m}) = \Psi (b) = z$
.) This is a contradiction, so
![]() $a \neq b$
. Now, we know that
$a \neq b$
. Now, we know that
![]() $(\phi '' x)([(-2b_{m+1} c_{m+1} + 1)n_{m}, (2b_{m+1} c_{m+1} - 1)n_{m})) = a^{2b_{m+1} c_{m+1} - 1} b^{2b_{m+1} c_{m+1} - 1}$
for
$(\phi '' x)([(-2b_{m+1} c_{m+1} + 1)n_{m}, (2b_{m+1} c_{m+1} - 1)n_{m})) = a^{2b_{m+1} c_{m+1} - 1} b^{2b_{m+1} c_{m+1} - 1}$
for
![]() $a \neq b \in A_{m}$
, and the only occurrence of such a word is with midpoint at the border between
$a \neq b \in A_{m}$
, and the only occurrence of such a word is with midpoint at the border between
![]() $A_{m+1}$
-words. Therefore,
$A_{m+1}$
-words. Therefore,
![]() $(\phi '' x)([-n_{m+1}, 0))$
and
$(\phi '' x)([-n_{m+1}, 0))$
and
![]() $(\phi '' x)([0, n_{m+1}))$
are
$(\phi '' x)([0, n_{m+1}))$
are
![]() $A_{m+1}$
-words, and so
$A_{m+1}$
-words, and so
![]() $\phi '' x$
has
$\phi '' x$
has
![]() $A_{m+1}$
-words at the same locations as x. Since
$A_{m+1}$
-words at the same locations as x. Since
![]() $\phi ''$
has range
$\phi ''$
has range
![]() $2n_k < n_{m+1}$
,
$2n_k < n_{m+1}$
,
![]() $\phi ''$
preserves locations of
$\phi ''$
preserves locations of
![]() $A_{m+1}$
-words by Lemma 4.5. This completes the induction and the proof.
$A_{m+1}$
-words by Lemma 4.5. This completes the induction and the proof.
The following lemma now completes the proof of Theorem 1.5.
Lemma 4.7. If
![]() $\phi \in \mathrm {Aut}(X, \sigma )$
preserves locations, then there exist
$\phi \in \mathrm {Aut}(X, \sigma )$
preserves locations, then there exist
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $h \in H_k$
so that
$h \in H_k$
so that
![]() $\phi = \phi _{k,h}$
.
$\phi = \phi _{k,h}$
.
Proof. Assume that
![]() $\phi \in \mathrm {Aut}(X,\sigma )$
preserves locations, fix k so that
$\phi \in \mathrm {Aut}(X,\sigma )$
preserves locations, fix k so that
![]() $\phi $
has range
$\phi $
has range
![]() $n_k$
, and let
$n_k$
, and let
![]() $\Phi $
be an inducing block map for
$\Phi $
be an inducing block map for
![]() $\phi $
. Choose any
$\phi $
. Choose any
![]() $x \in X$
with
$x \in X$
with
![]() $x([0, n_k))$
an
$x([0, n_k))$
an
![]() $A_k$
-word. Then
$A_k$
-word. Then
![]() $x([in_k, (i+1)n_k))$
is an
$x([in_k, (i+1)n_k))$
is an
![]() $A_k$
-word for all i, and by assumption,
$A_k$
-word for all i, and by assumption,
![]() $(\phi x)([in_k, (i+1)n_k))$
is an
$(\phi x)([in_k, (i+1)n_k))$
is an
![]() $A_k$
-word for all i as well. Then, exactly as in the proof of Lemma 4.5, for all
$A_k$
-word for all i as well. Then, exactly as in the proof of Lemma 4.5, for all
![]() $u,v,w \in A_k$
with
$u,v,w \in A_k$
with
![]() $u=v$
or
$u=v$
or
![]() $v=w$
,
$v=w$
,
![]() $\Phi (uvw) \in A_k$
. We will prove that
$\Phi (uvw) \in A_k$
. We will prove that
![]() $\phi $
is equal to some
$\phi $
is equal to some
![]() $\phi _{k,h}$
in two steps. First, we will show that
$\phi _{k,h}$
in two steps. First, we will show that
![]() $\Phi (uvw)$
depends only on v, implying that
$\Phi (uvw)$
depends only on v, implying that
![]() $\phi $
is induced by a permutation of
$\phi $
is induced by a permutation of
![]() $A_k$
-words in the sense of equation (12). Then, we show that the only such permutations which send
$A_k$
-words in the sense of equation (12). Then, we show that the only such permutations which send
![]() $A_{k+1}$
-words to
$A_{k+1}$
-words to
![]() $A_{k+1}$
-words are of the form
$A_{k+1}$
-words are of the form
![]() $\pi _{k,h}$
.
$\pi _{k,h}$
.
To see that
![]() $\Phi (uvw)$
depends only on v, choose any
$\Phi (uvw)$
depends only on v, choose any
![]() $(u,v,w) \neq (u', v, w') \in S$
. By its definition, the
$(u,v,w) \neq (u', v, w') \in S$
. By its definition, the
![]() $A_{k+1}$
-word
$A_{k+1}$
-word
 $w_{\mathrm {id}}^{(k+1)}$
contains both
$w_{\mathrm {id}}^{(k+1)}$
contains both
![]() $uvw$
and
$uvw$
and
![]() $u'vw'$
somewhere in its first
$u'vw'$
somewhere in its first
![]() $(2b_{k+1} c_{k+1} + b_{k+1}|A_k|^2)$
concatenated
$(2b_{k+1} c_{k+1} + b_{k+1}|A_k|^2)$
concatenated
![]() $A_k$
-words, say that
$A_k$
-words, say that
 $w_{\mathrm {id}}^{(k+1)}([(p-1)n_k, (p+2)n_k)) = uvw$
and
$w_{\mathrm {id}}^{(k+1)}([(p-1)n_k, (p+2)n_k)) = uvw$
and
 $w_{\mathrm {id}}^{(k+1)}([(q-1)n_k, (q+2)n_k)) = u'vw'$
for some
$w_{\mathrm {id}}^{(k+1)}([(q-1)n_k, (q+2)n_k)) = u'vw'$
for some
![]() $p,q \leq 2b_{k+1} c_{k+1} + b_{k+1}|A_k|^2$
.
$p,q \leq 2b_{k+1} c_{k+1} + b_{k+1}|A_k|^2$
.
Choose any
![]() $x \in X$
with
$x \in X$
with
 $x([0, n_{k+1})) = w_{\mathrm {id}}^{(k+1)}$
. Since
$x([0, n_{k+1})) = w_{\mathrm {id}}^{(k+1)}$
. Since
![]() $\phi $
preserves locations of
$\phi $
preserves locations of
![]() $A_{k+1}$
-words,
$A_{k+1}$
-words,
![]() $(\phi x)([0, n_{k+1}))$
is some
$(\phi x)([0, n_{k+1}))$
is some
![]() $A_{k+1}$
-word
$A_{k+1}$
-word
 $w_{h r_i^{(k+1)}}^{(k+1)} = \pi _{k,h} w_{r_i^{(k+1)}}^{(k+1)}$
with
$w_{h r_i^{(k+1)}}^{(k+1)} = \pi _{k,h} w_{r_i^{(k+1)}}^{(k+1)}$
with
![]() $h \in H_k$
and
$h \in H_k$
and
![]() $1 \leq i \leq q_{k+1}$
. Note that
$1 \leq i \leq q_{k+1}$
. Note that
 $w_{r_i^{(k+1)}}^{(k+1)}$
begins with the same initial
$w_{r_i^{(k+1)}}^{(k+1)}$
begins with the same initial
![]() $2b_{k+1} c_{k+1} + b_{k+1}|A_k|^2$
concatenated
$2b_{k+1} c_{k+1} + b_{k+1}|A_k|^2$
concatenated
![]() $A_k$
-words as
$A_k$
-words as
 $w_{\mathrm {id}}^{(k+1)}$
, and so contains v starting at locations
$w_{\mathrm {id}}^{(k+1)}$
, and so contains v starting at locations
![]() $pn_k$
and
$pn_k$
and
![]() $qn_k$
. However,
$qn_k$
. However,
![]() $\pi _{k,h}$
is just a permutation of
$\pi _{k,h}$
is just a permutation of
![]() $A_k$
-words, and so
$A_k$
-words, and so
 $w_{h r_i^{(k+1)}}^{(k+1)}$
contains the same
$w_{h r_i^{(k+1)}}^{(k+1)}$
contains the same
![]() $A_k$
-word
$A_k$
-word
![]() $\pi _{k,h}(v)$
at those locations. Therefore,
$\pi _{k,h}(v)$
at those locations. Therefore,
![]() $\Phi (uvw) = \Phi (u'vw') = \pi _{k,h}(v)$
. Since
$\Phi (uvw) = \Phi (u'vw') = \pi _{k,h}(v)$
. Since
![]() $(u,v,w)$
and
$(u,v,w)$
and
![]() $(u', v, w')$
were arbitrary, we have shown that
$(u', v, w')$
were arbitrary, we have shown that
![]() $\Phi (uvw)$
depends only on v, that is there is a permutation
$\Phi (uvw)$
depends only on v, that is there is a permutation
![]() $\tau $
of
$\tau $
of
![]() $A_k$
-words so that
$A_k$
-words so that
![]() $\phi = \alpha _{\tau }$
as in equation (12).
$\phi = \alpha _{\tau }$
as in equation (12).
Consider the image of the
![]() $A_{k+1}$
-word
$A_{k+1}$
-word
 $w_{\mathrm {id}}^{(k+1)}$
under (coordinatewise application of)
$w_{\mathrm {id}}^{(k+1)}$
under (coordinatewise application of)
![]() $\phi = \alpha _\tau $
. It must be another
$\phi = \alpha _\tau $
. It must be another
![]() $A_{k+1}$
-word since
$A_{k+1}$
-word since
![]() $\phi $
preserves locations, call it
$\phi $
preserves locations, call it
 $w_{h r_i^{(k+1)}}^{(k+1)}$
for
$w_{h r_i^{(k+1)}}^{(k+1)}$
for
![]() $h \in H_k$
and
$h \in H_k$
and
![]() $1 \leq i \leq q_{k+1}$
. We note that
$1 \leq i \leq q_{k+1}$
. We note that
 $w_{h_2^{(k)}}^{(k)}$
occurs
$w_{h_2^{(k)}}^{(k)}$
occurs
![]() $b_{k+1} (5q_{k+1} + |A_k| - 1)$
times in the decomposition of
$b_{k+1} (5q_{k+1} + |A_k| - 1)$
times in the decomposition of
 $w_{\mathrm {id}}^{(k+1)}$
into
$w_{\mathrm {id}}^{(k+1)}$
into
![]() $A_{k}$
-words, and so some
$A_{k}$
-words, and so some
![]() $A_k$
-word must appear this many times in
$A_k$
-word must appear this many times in
 $w_{h r_i^{(k+1)}}^{(k+1)}$
. It is not hard to check that this implies
$w_{h r_i^{(k+1)}}^{(k+1)}$
. It is not hard to check that this implies
![]() $i = 1$
(the maximum number of times an
$i = 1$
(the maximum number of times an
![]() $A_k$
-word appears becomes smaller if
$A_k$
-word appears becomes smaller if
![]() $i> 1$
, since then the final self-concatenation in the definition of
$i> 1$
, since then the final self-concatenation in the definition of
 $w_{h r_i^{(k+1)}}^{(k+1)}$
is shorter). Therefore,
$w_{h r_i^{(k+1)}}^{(k+1)}$
is shorter). Therefore,
 $\Phi (w_{\mathrm {id}}^{(k+1)}) = w_{h r_1^{(k+1)}}^{(k+1)} = w_h^{(k+1)}$
for some
$\Phi (w_{\mathrm {id}}^{(k+1)}) = w_{h r_1^{(k+1)}}^{(k+1)} = w_h^{(k+1)}$
for some
![]() $h \in H_k$
.
$h \in H_k$
.
Recall that
 $w_{\mathrm {id}}^{(k+1)}$
contains every
$w_{\mathrm {id}}^{(k+1)}$
contains every
![]() $A_k$
-word, and so since
$A_k$
-word, and so since
![]() $\phi = \alpha _\tau $
and
$\phi = \alpha _\tau $
and
![]() $\pi _{k,h}$
map
$\pi _{k,h}$
map
 $w_{\mathrm {id}}^{(k+1)}$
to the same word
$w_{\mathrm {id}}^{(k+1)}$
to the same word
 $w_h^{(k+1)}$
, it must be the case that
$w_h^{(k+1)}$
, it must be the case that
![]() $\tau = \pi _{k,h}$
. Therefore,
$\tau = \pi _{k,h}$
. Therefore,
![]() $\phi = \phi _{k,h}$
, and since
$\phi = \phi _{k,h}$
, and since
![]() $\phi $
was arbitrary, we are done.
$\phi $
was arbitrary, we are done.
By Lemmas 4.6 and 4.7, every
![]() $\phi \in \mathrm {Aut}(X, \sigma )$
can be written as
$\phi \in \mathrm {Aut}(X, \sigma )$
can be written as
![]() $\sigma ^j \phi _{k,h}$
for some
$\sigma ^j \phi _{k,h}$
for some
![]() $j \in \mathbb {Z}$
,
$j \in \mathbb {Z}$
,
![]() $k \in \mathbb {N}$
, and
$k \in \mathbb {N}$
, and
![]() $h \in H_k$
, and so
$h \in H_k$
, and so
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is isomorphic to G, completing the proof.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$
is isomorphic to G, completing the proof.
Remark 4.8. We can in fact say a little more about
![]() $\mathrm {Aut}(X,\sigma )$
for this construction:
$\mathrm {Aut}(X,\sigma )$
for this construction:
![]() $\mathrm {Aut}(X,\sigma )$
is isomorphic to
$\mathrm {Aut}(X,\sigma )$
is isomorphic to
![]() $\mathbb {Z} \times G$
, with the
$\mathbb {Z} \times G$
, with the
![]() $\mathbb {Z}$
corresponding to
$\mathbb {Z}$
corresponding to
![]() $\sigma $
. To see this, recall that G is isomorphic to
$\sigma $
. To see this, recall that G is isomorphic to
![]() $G_{\phi }$
, and then consider the map
$G_{\phi }$
, and then consider the map
![]() $\alpha \colon G_{\phi } \times \mathbb {Z} \to \mathrm {Aut}(X,\sigma )$
defined by
$\alpha \colon G_{\phi } \times \mathbb {Z} \to \mathrm {Aut}(X,\sigma )$
defined by
![]() $\alpha (\phi _{h,k},n) = \phi _{h,k}\sigma ^{n}$
. It is easy to check that since
$\alpha (\phi _{h,k},n) = \phi _{h,k}\sigma ^{n}$
. It is easy to check that since
![]() $\sigma $
is in the center of
$\sigma $
is in the center of
![]() $\mathrm {Aut}(X,\sigma )$
,
$\mathrm {Aut}(X,\sigma )$
,
![]() $\alpha $
is a homomorphism. Lemmas 4.6 and 4.7 imply that
$\alpha $
is a homomorphism. Lemmas 4.6 and 4.7 imply that
![]() $\alpha $
is surjective, and it is straightforward to check that
$\alpha $
is surjective, and it is straightforward to check that
![]() $\alpha $
is also injective, and hence an isomorphism.
$\alpha $
is also injective, and hence an isomorphism.
Remark 4.9. It is natural to wonder whether the somewhat complex block concatenation subshifts could be replaced by the simpler subclass of Toeplitz subshifts in our constructions. In general, this is not possible, since the automorphism group of a Toeplitz subshift is always abelian (see [Reference Donoso, Durand, Maass and Petite8]).
Remark 4.10. In Example 3.9 from [Reference Boyle, Lind and Rudolph2], they construct a minimal subshift X where the additive group of rationals
![]() $\mathbb {Q}$
embeds into
$\mathbb {Q}$
embeds into
![]() $\mathrm {Aut}(X,\sigma )$
(and outline alterations which would make this embedding an isomorphism). Since
$\mathrm {Aut}(X,\sigma )$
(and outline alterations which would make this embedding an isomorphism). Since
![]() ${\mathbb {Q}}/{\mathbb {Z}}$
is countable and locally finite, Theorem 1.5 provides a different minimal subshift X with
${\mathbb {Q}}/{\mathbb {Z}}$
is countable and locally finite, Theorem 1.5 provides a different minimal subshift X with
![]() ${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }} = {\mathbb {Q}}/{\mathbb {Z}}$
.
${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }} = {\mathbb {Q}}/{\mathbb {Z}}$
.
Acknowledgement
R.P. gratefully acknowledges the support of a Simons Foundation Collaboration Grant.