Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Derksen, H.
and
Masser, D.
2015.
Linear equations over multiplicative groups, recurrences, and mixing II.
Indagationes Mathematicae,
Vol. 26,
Issue. 1,
p.
113.
Тихонов, Сергей Викторович
and
Tikhonov, Sergei Viktorovich
2015.
Об отсутствии кратного перемешивания и централизаторе сохраняющих меру действий.
Математические заметки,
Vol. 97,
Issue. 4,
p.
636.
Tikhonov, S. V.
2015.
On the absence of multiple mixing and on the centralizer of measure-preserving actions.
Mathematical Notes,
Vol. 97,
Issue. 3-4,
p.
652.
Baake, Michael
A. G. Roberts, John
and
Yassawi, Reem
2018.
Reversing and extended symmetries of shift spaces.
Discrete & Continuous Dynamical Systems - A,
Vol. 38,
Issue. 2,
p.
835.
DERKSEN, H.
and
MASSER, D.
2018.
Linear equations over multiplicative groups, recurrences, and mixing III.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 7,
p.
2625.
ARENAS-CARMONA, L.
BEREND, D.
and
BERGELSON, V.
2019.
An almost mixing of all orders property of algebraic dynamical systems.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 5,
p.
1211.
Ward, Tom
2020.
Encyclopedia of Complexity and Systems Science.
p.
1.
Ward, Tom
2023.
Ergodic Theory.
p.
577.
BERGELSON, V.
and
ZELADA, R.
2024.
Strongly mixing systems are almost strongly mixing of all orders.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 6,
p.
1489.

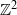 -action which is 2-mixing but not 3-mixing. Our main result is that, excluding certain small ‘constructible’ sets, the system is mixing of every order.
-action which is 2-mixing but not 3-mixing. Our main result is that, excluding certain small ‘constructible’ sets, the system is mixing of every order.