Hostname: page-component-76c49bb84f-6sxsx Total loading time: 0 Render date: 2025-07-09T01:47:00.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Joint ergodicity along generalized linear functions

Published online by Cambridge University Press:  15 June 2015

V. BERGELSON ,
A. LEIBMAN  and
Y. SON
V. BERGELSON
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email bergelson.1@osu.edu, leibman.1@osu.edu
A. LEIBMAN
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email bergelson.1@osu.edu, leibman.1@osu.edu
Y. SON
Affiliation:
Faculty of Mathematics and Computer Science, The Weizmann Institute of Science, 234 Herzl Street, Rehovot 7610001, Israel email younghwan.son@weizmann.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

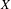A criterion of joint ergodicity of several sequences of transformations of a probability measure space $X$ of the form 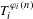$T_{i}^{\unicode[STIX]{x1D711}_{i}(n)}$ is given for the case where 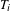$T_{i}$ are commuting measure-preserving transformations of 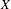$X$ and 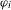$\unicode[STIX]{x1D711}_{i}$ are integer-valued generalized linear functions, that is, the functions formed from conventional linear functions by an iterated use of addition, multiplication by constants, and the greatest integer function. We also establish a similar criterion for joint ergodicity of families of transformations depending on a continuous parameter, as well as a condition of joint ergodicity of sequences 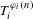$T_{i}^{\unicode[STIX]{x1D711}_{i}(n)}$ along primes.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 7 , October 2016 , pp. 2044 - 2075
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berend, D.. Joint ergodicity and mixing. J. Anal. Math. 45 (1985), 255–284.Google Scholar
Berend, D. and Bergelson, V.. Jointly ergodic measure preserving transformations. Israel J. Math. 49(4) (1984), 307–314.CrossRefGoogle Scholar
Berend, D. and Bergelson, V.. Characterization of joint ergodicity for non-commuting transformations. Israel J. Math. 56(1) (1986), 123–128.Google Scholar
Bergelson, V.. Weakly mixing PET. Ergod. Th. & Dynam. Sys. 7(3) (1987), 337–349.CrossRefGoogle Scholar
Bergelson, V. and Gorodnik, A.. Weakly mixing group actions: a brief survey and an example. Modern Dynamical Systems and Applications. Cambridge University Press, New York, 2004, pp. 3–25.Google Scholar
Bergelson, V. and Håland Knutson, I. J.. Weak mixing implies weak mixing of higher orders along tempered functions. Ergod. Th. & Dynam. Sys. 29(5) (2009), 1375–1416.Google Scholar
Bergelson, V. and Leibman, A.. Polynomial extensions of van der Waerden’s and Szemeredi’s theorems. J. Amer. Math. Soc. 9 (1996), 725–753.Google Scholar
Bergelson, V. and Leibman, A.. Distribution of values of bounded generalized polynomials. Acta Math. 198 (2007), 155–230.CrossRefGoogle Scholar
Bergelson, V., Leibman, A. and Moreira, C. G.. From discrete- to continuous-time ergodic theorems. Ergod. Th. & Dynam. Sys. 32(2) (2012), 383–426.CrossRefGoogle Scholar
Bergelson, V. and McCutcheon, R.. Uniformity in the polynomial Szemeredi theorem. Ergodic Theory of ℤ d Actions (London Mathematical Society, Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 273–296.Google Scholar
Bergelson, V. and Rosenblatt, J.. Mixing actions of groups. Illinois J. Math. 32(1) (1988), 65–80.Google Scholar
Frantzikinakis, N.. Multiple recurrence and convergence for Hardy sequences of polynomial growth. J. Anal. Math. 112 (2010), 79–135.Google Scholar
Frantzikinakis, N., Host, B. and Kra, B.. Multiple recurrence and convergence for sequences related to prime numbers. J. Reine Angew. Math. 611 (2007), 131–144.Google Scholar
Frantzikinakis, N. and Kra, B.. Ergodic averages for independent polynomials and applications. J. Lond. Math. Soc. (2) 74 (2006), 131–142.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Green, B. and Tao, T.. Linear equations in primes. Ann. of Math. (2) 171(3) (2010), 1753–1850.CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T.. An inverse theorem for the Gowers U s+1 -norm. Ann. of Math. 176(2) (2012), 1231–1372.Google Scholar
Sun, W.. Multiple recurrence and convergence for certain averages along shifted primes. Ergod. Th. & Dynam. Sys., available on CJO2014, doi:10.1017/etds.2014.6.Google Scholar
von Neumann, J. and Koopman, B. O.. Dynamical systems of continuous spectra. Proc. Natl. Acad. Sci. USA 18 (1932), 255–263.Google Scholar