1 Introduction
The purpose of this paper is to establish the concept of Hubbard trees for post-singularly finite exponential maps, that is, maps of the form
![]() $E_{\lambda }\colon z\mapsto \lambda \exp (z)$
for which the orbit of the singular value
$E_{\lambda }\colon z\mapsto \lambda \exp (z)$
for which the orbit of the singular value
![]() $0$
is finite. While Hubbard trees are known to be an extremely useful concept for the dynamics of polynomials, so far they have not been introduced for the dynamics of entire functions. Part of the problem is that asymptotic values might prevent the existence of Hubbard trees in the strict traditional sense, as invariant compact trees in the plane, and they do so even for exponential maps. We therefore introduce a modified concept that we call homotopy Hubbard trees and demonstrate their use for the study of exponential maps. Exponential maps have received a lot of attention over the years, and an understanding of exponential dynamics has often proved to be useful for the study of much more general classes of transcendental entire functions.
$0$
is finite. While Hubbard trees are known to be an extremely useful concept for the dynamics of polynomials, so far they have not been introduced for the dynamics of entire functions. Part of the problem is that asymptotic values might prevent the existence of Hubbard trees in the strict traditional sense, as invariant compact trees in the plane, and they do so even for exponential maps. We therefore introduce a modified concept that we call homotopy Hubbard trees and demonstrate their use for the study of exponential maps. Exponential maps have received a lot of attention over the years, and an understanding of exponential dynamics has often proved to be useful for the study of much more general classes of transcendental entire functions.
This project goes back to the Bachelor’s thesis of the second named author [Reference RothgangR]. Previously, Hubbard trees were defined only for post-critically finite polynomials in [Reference Douady and HubbardDH1]. The Hubbard tree is the unique smallest tree embedded in the filled-in Julia set that contains all critical points of the polynomial and is forward invariant under its dynamics (and in addition normalized on bounded Fatou components). It turns out that this definition does not immediately generalize to exponential maps: because of the existence of an asymptotic value, an exponential map cannot have an exactly forward invariant tree containing the post-singular set. We solve this by only requiring the tree to be invariant up to homotopy relative to the post-singular set. Because of the relaxed invariance condition, we call the resulting tree a homotopy Hubbard tree. In analogy to polynomials, the underlying abstract graph of a homotopy Hubbard tree, together with the dynamics of its self-map on the vertices and a finite amount of extra information, is a useful combinatorial object. Specifically for exponential maps, we call this an abstract exponential Hubbard tree. The main results of our paper can be phrased as follows.
Main Theorem 1.1. Every post-singularly finite exponential map has a homotopy Hubbard tree, and this tree is unique up to homotopy relative to the post-singular set. Moreover, for every abstract exponential Hubbard tree, there is a unique post-singularly finite exponential map realizing it.
Hubbard trees are a convenient tool to read off the dynamical properties of the map under consideration (an example is given below). Additionally, abstract Hubbard trees provide a way to define the notion of core entropy (introduced by Thurston [Reference Thurston, Bonifant, Lyubich and SutherlandT] for post-critically finite polynomials) for post-singularly finite parameters and to study properties of the core entropy function on the parameter space. This has been done for quadratic polynomials in [Reference Dudko and SchleicherDS] and independently in [Reference TiozzoTi]. While entropy of transcendental mappings is always infinite [Reference Benini, Fornæss and PetersBFP], core entropy of post-singularly finite exponential mappings is always bounded by
![]() $\log {2}$
[Reference HasslerHa]. This provides relevant information to the dynamics, in a similar sense that entropy of degree d polynomials always equals
$\log {2}$
[Reference HasslerHa]. This provides relevant information to the dynamics, in a similar sense that entropy of degree d polynomials always equals
![]() $\log {d}$
, while core entropy allows to distinguish different polynomial dynamical systems.
$\log {d}$
, while core entropy allows to distinguish different polynomial dynamical systems.
We want to point out that the construction of homotopy Hubbard trees in this paper is quite explicit. Given the external address of a dynamic ray landing at the singular value, we show how to construct the abstract exponential Hubbard tree of the corresponding map algorithmically.
Post-singularly finite exponential maps have already been classified in [Reference Laubner, Schleicher and VicolLSV] in terms of the external addresses of the dynamic rays landing at the singular value. Compared to this previous classification, our result has the advantage that it establishes a bijection between the class of maps and the instances of the combinatorial model: while several addresses might correspond to the same exponential map, there is a natural bijection between abstract exponential Hubbard trees and post-singularly finite exponential maps. Also, some dynamical properties of the map are obtained more easily from the abstract Hubbard tree than from an external address. For example, the abstract Hubbard tree contains information about all periodic branch points of the Julia set, while it is computationally intensive to determine them from the external address.
Although we restrict to exponential maps in this article, our results have wider implications. Indeed, the insights gained here, together with recent findings on the structure of the escaping sets of entire functions with bounded post-singular set established in [Reference Benini and RempeBR], have lead to a general theory of homotopy Hubbard trees for all post-singularly finite transcendental entire functions. This is the content of the first named author’s PhD thesis [Reference PfrangPf]. The first part of this thesis is available at [Reference Pfrang, Petrat and SchleicherPPS].
1.1 Background and relevance
The dynamics of a holomorphic map is controlled to a large extent by the orbits of its singular values (see [Reference MilnorM] for a general introduction to holomorphic dynamical systems and [Reference SchleicherS2] specifically for transcendental entire functions). Singular values are points in the range of the function that do not have a neighborhood on which all branches of the inverse function are well defined and biholomorphic. For a polynomial
![]() $f\colon \mathbb {C}\to \mathbb {C}$
, every singular value is a critical value, that is, a point
$f\colon \mathbb {C}\to \mathbb {C}$
, every singular value is a critical value, that is, a point
![]() $w\in \mathbb {C}$
such that
$w\in \mathbb {C}$
such that
![]() $f'(z)=0$
for some
$f'(z)=0$
for some
![]() $z\in f^{-1}(w)$
. For a transcendental entire function
$z\in f^{-1}(w)$
. For a transcendental entire function
![]() $f\colon \mathbb {C}\to \mathbb {C}$
, a singular value can also be an asymptotic value or a limit point of asymptotic and critical values. A point
$f\colon \mathbb {C}\to \mathbb {C}$
, a singular value can also be an asymptotic value or a limit point of asymptotic and critical values. A point
![]() $w\in \mathbb {C}$
is called an asymptotic value if there exists a curve
$w\in \mathbb {C}$
is called an asymptotic value if there exists a curve
![]() $\gamma \colon [0,+\infty )\to \mathbb {C}$
satisfying
$\gamma \colon [0,+\infty )\to \mathbb {C}$
satisfying
![]() $\lim _{t\to +\infty }\gamma (t)=\infty $
and
$\lim _{t\to +\infty }\gamma (t)=\infty $
and
![]() $\lim _{t\to +\infty }f(\gamma (t))=w$
. In any parameter space of holomorphic functions, the easiest maps to understand are those for which all singular values have finite orbits. These functions are called post-singularly finite (or post-critically finite in the case of polynomials). Not only are they the dynamically simplest maps, but also, in many cases, the most important ones for the structure of the parameter space. Figuratively, one reason for studying them is because ‘it is easier to search for your lost keys under a lamp post, but there are lamp posts at every important street intersection so they are very helpful to find your way around’. We explain this by way of analogy to the simplest and best-studied space of polynomial maps, the space of quadratic polynomials
$\lim _{t\to +\infty }f(\gamma (t))=w$
. In any parameter space of holomorphic functions, the easiest maps to understand are those for which all singular values have finite orbits. These functions are called post-singularly finite (or post-critically finite in the case of polynomials). Not only are they the dynamically simplest maps, but also, in many cases, the most important ones for the structure of the parameter space. Figuratively, one reason for studying them is because ‘it is easier to search for your lost keys under a lamp post, but there are lamp posts at every important street intersection so they are very helpful to find your way around’. We explain this by way of analogy to the simplest and best-studied space of polynomial maps, the space of quadratic polynomials
![]() $p_c\colon z\mapsto z^2+c$
for
$p_c\colon z\mapsto z^2+c$
for
![]() $c\in \mathbb {C}$
. Its connectedness locus is the Mandelbrot set
$c\in \mathbb {C}$
. Its connectedness locus is the Mandelbrot set
All branch points of the Mandelbrot set (in a sense made precise in [Reference SchleicherS1, Theorem 3.1]) are post-critically finite parameters, and under the assumption that the Mandelbrot set is locally connected (the famous MLC conjecture), these branch points completely describe its topology. In the space of exponential maps, post-singularly finite parameters play a comparable role.
Naturally, much work has gone into investigating the dynamics of post-singularly finite holomorphic functions. For rational maps, a deep characterization theorem by Thurston [Reference Douady and HubbardDH2] about branched self-covers of the sphere that arise from rational maps has made strong classification results possible. Post-critically finite polynomials [Reference PoirierP] and, quite recently, post-critically finite Newton maps [Reference Lodge, Mikulich and SchleicherLMS1, Reference Lodge, Mikulich and SchleicherLMS2] have been completely classified in terms of custom-tailored combinatorial models using Thurston’s theorem.
The fundamental idea of classifying post-critically finite polynomials in terms of their Hubbard trees originated from [Reference Douady and HubbardDH1]. Their program has been carried through in greater generality in [Reference Bielefeld, Fisher and HubbardBFH] and in full generality in [Reference PoirierP]. The following finite amount of combinatorial information is sufficient to completely describe the dynamics of a post-critically finite polynomial:
-
• the graph structure of its Hubbard tree (without an embedding into the complex plane);
-
• the dynamics of the polynomial on the finite set of vertices of the tree;
-
• the degrees of the critical points of the polynomial; and
-
• for each vertex, certain (combinatorial) angles between the edges incident to this vertex.
This combinatorial data distinguish all post-critically finite polynomials. Conversely, if we start with an expansive (in a sense, defined in Definition 3.8) dynamical tree with consistent degree and angle information (this finite combinatorial object is known as an abstract Hubbard tree), there exists a post-critically finite polynomial realizing this tree, and this map is unique up to affine conjugation. Therefore, there exists a natural bijection between post-critically finite polynomials (up to affine equivalence) and abstract Hubbard trees. In the spirit of this classification, we establish a natural bijection between post-singularly finite exponential maps and abstract exponential Hubbard trees in §6.
1.2 Structure of the article
In §2, we give a combinatorial description of the escaping set of exponential maps and its dynamics in terms of external addresses. Path-connected components of the escaping set are called dynamic rays; topologically, they are arcs terminating at
![]() $\infty $
(in
$\infty $
(in
![]() $\overline {\mathbb {C}}$
). The pre-images of a dynamic ray landing at the singular value form the boundaries of the dynamic partition. Itineraries with respect to this partition distinguish (pre-)periodic points and determine which dynamic rays have a common landing point.
$\overline {\mathbb {C}}$
). The pre-images of a dynamic ray landing at the singular value form the boundaries of the dynamic partition. Itineraries with respect to this partition distinguish (pre-)periodic points and determine which dynamic rays have a common landing point.
In §3, we motivate the concept of homotopy Hubbard trees and give a precise definition of homotopy Hubbard trees for exponential maps. Some technical results on homotopies of embedded trees needed in this paper are discussed.
In §4, we show that a homotopy Hubbard tree can be chosen to not intersect dynamic rays landing at post-singular points. Furthermore, the itinerary of the singular value with respect to a dynamical partition determines the graph structure and the dynamics of the tree. Together, these two facts imply uniqueness of homotopy Hubbard trees.
Section 5 deals with the construction of homotopy Hubbard trees. The combinatorial description of dynamic rays from §2 is used to show that every triple of post-singular points is separated by dynamic rays landing at a common (pre-)periodic point. Connecting the post-singular set without intersecting these separating rays yields a homotopy Hubbard tree.
Finally, in §6, we give a combinatorial classification of post-singularly finite exponential maps in terms of abstract Hubbard trees using the transcendental analogue of Thurston’s characterization theorem for rational maps established in [Reference Hubbard, Schleicher and ShishikuraHSS]. In §7, we discuss possible extensions and generalizations.
1.3 Notation and terminology
The complex plane is denoted by
![]() $\mathbb {C}$
and the Riemann sphere by
$\mathbb {C}$
and the Riemann sphere by
![]() $\overline {\mathbb {C}}$
. We denote the trace of a curve g by
$\overline {\mathbb {C}}$
. We denote the trace of a curve g by
![]() $\operatorname {\mathrm {Tr}}(g)$
. An arc is a simple (injective) curve and a Jordan curve is a simple closed curve. A (pre-)periodic point is a point that is either periodic or pre-periodic under iteration of the map under consideration. We use the term ‘pre-periodic’ in the sense of ‘strictly pre-periodic’, that is, excluding the periodic case.
$\operatorname {\mathrm {Tr}}(g)$
. An arc is a simple (injective) curve and a Jordan curve is a simple closed curve. A (pre-)periodic point is a point that is either periodic or pre-periodic under iteration of the map under consideration. We use the term ‘pre-periodic’ in the sense of ‘strictly pre-periodic’, that is, excluding the periodic case.
2 Background on the dynamics of exponential maps
In the following, let
![]() $f\colon \mathbb {C}\to \mathbb {C}$
denote an entire function. The singular set
$f\colon \mathbb {C}\to \mathbb {C}$
denote an entire function. The singular set
![]() $S(f)$
of f is defined to be the closure of the set of critical and asymptotic values of f. It is the smallest subset of
$S(f)$
of f is defined to be the closure of the set of critical and asymptotic values of f. It is the smallest subset of
![]() $\mathbb {C}$
such that the restriction of f to
$\mathbb {C}$
such that the restriction of f to
![]() $\mathbb {C}\setminus f^{-1}(S(f))$
is a covering map (see e.g. [Reference Goldberg and KeenGK, Lemma 1.1]). The post-singular set
$\mathbb {C}\setminus f^{-1}(S(f))$
is a covering map (see e.g. [Reference Goldberg and KeenGK, Lemma 1.1]). The post-singular set
![]() $P(f)$
of f is given by
$P(f)$
of f is given by
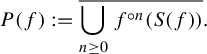 $$ \begin{align*} P(f):=\overline{\bigcup_{n\geq 0}f^{\circ n}(S(f))}. \end{align*} $$
$$ \begin{align*} P(f):=\overline{\bigcup_{n\geq 0}f^{\circ n}(S(f))}. \end{align*} $$
We call the function f post-singularly finite if
![]() $\vert P(f)\vert <\infty $
.
$\vert P(f)\vert <\infty $
.
Entire functions have an important forward and backward invariant set, the set of escaping points; it is often more important than Fatou and Julia sets because it is never empty and never all of
![]() $\mathbb {C}$
(see [Reference EremenkoE1]), so it provides a non-trivial dynamically invariant decomposition of
$\mathbb {C}$
(see [Reference EremenkoE1]), so it provides a non-trivial dynamically invariant decomposition of
![]() $\mathbb {C}$
. Here is the formal definition.
$\mathbb {C}$
. Here is the formal definition.
Definition 2.1. (Escaping set)
The escaping set of f is given by
In [Reference Rottenfusser, Rückert, Rempe and SchleicherRRRS], it was shown that for a large class of transcendental entire functions (finite compositions of functions of bounded type and finite order), the escaping set is organized in the form of disjoint dynamic rays, which are certain arcs consisting of escaping points that terminate at
![]() $\infty $
.
$\infty $
.
Definition 2.2. (Ray tails, dynamic rays, and landing points)
A ray tail of f is an injective curve
![]() $g\colon [\tau ,\infty )\to I(f)$
(
$g\colon [\tau ,\infty )\to I(f)$
(
![]() $\tau \in \mathbb {R}$
) such that for each
$\tau \in \mathbb {R}$
) such that for each
![]() $n\in \mathbb {N}$
, the restriction
$n\in \mathbb {N}$
, the restriction
![]() $f^{\circ n}|_g$
is injective,
$f^{\circ n}|_g$
is injective,
![]() $\lim _{t\to \infty }f^{\circ n}(g(t))=\infty $
, and
$\lim _{t\to \infty }f^{\circ n}(g(t))=\infty $
, and
![]() $f^{\circ n}(g(t))\to \infty $
as
$f^{\circ n}(g(t))\to \infty $
as
![]() $n\to \infty $
uniformly in t.
$n\to \infty $
uniformly in t.
A dynamic ray of f is a maximal (in the sense of inclusions of sets) injective curve
![]() $g\colon (\tau _0,\infty )\to I(f)$
such that
$g\colon (\tau _0,\infty )\to I(f)$
such that
![]() $g|_{[\tau ,\infty )}$
is a ray tail for every
$g|_{[\tau ,\infty )}$
is a ray tail for every
![]() $\tau>\tau _0$
. We say that the dynamic ray g lands at the point
$\tau>\tau _0$
. We say that the dynamic ray g lands at the point
![]() $z\in \mathbb {C}$
if
$z\in \mathbb {C}$
if
![]() $\lim _{t\to \tau _0}g(t)=z$
; in this case, z is called the landing point of g.
$\lim _{t\to \tau _0}g(t)=z$
; in this case, z is called the landing point of g.
We call the dynamic ray g periodic if
![]() $f^{\circ n}(\operatorname {\mathrm {Tr}}(g))\subseteq \operatorname {\mathrm {Tr}}(g)$
for some
$f^{\circ n}(\operatorname {\mathrm {Tr}}(g))\subseteq \operatorname {\mathrm {Tr}}(g)$
for some
![]() $n\in \mathbb {N}$
; we call it pre-periodic if some forward iterate
$n\in \mathbb {N}$
; we call it pre-periodic if some forward iterate
![]() $f^{\circ k}(g)$
of the ray g (which, by definition, is again a dynamic ray) is periodic, but not g itself.
$f^{\circ k}(g)$
of the ray g (which, by definition, is again a dynamic ray) is periodic, but not g itself.
In this paper, we focus on the case of post-singularly finite (psf) exponential maps: these are (up to affine conjugation) maps of the form
![]() $E_{\lambda }\colon \mathbb {C}\to \mathbb {C}$
,
$E_{\lambda }\colon \mathbb {C}\to \mathbb {C}$
,
![]() $E_{\lambda }(z)=\lambda \exp (z)$
, where the parameter
$E_{\lambda }(z)=\lambda \exp (z)$
, where the parameter
![]() $\lambda \in \mathbb {C}\setminus \{0\}$
is chosen such that the orbit of the only singular value
$\lambda \in \mathbb {C}\setminus \{0\}$
is chosen such that the orbit of the only singular value
![]() $0$
is finite and hence strictly pre-periodic (the orbit of
$0$
is finite and hence strictly pre-periodic (the orbit of
![]() $0$
cannot be periodic because
$0$
cannot be periodic because
![]() $0$
is an omitted value). For these functions, the set of escaping points has been described and classified in [Reference Schleicher and ZimmerSZ1], using the combinatorial concept of external addresses that distinguish dynamic rays.
$0$
is an omitted value). For these functions, the set of escaping points has been described and classified in [Reference Schleicher and ZimmerSZ1], using the combinatorial concept of external addresses that distinguish dynamic rays.
Definition 2.3. (External addresses and the shift map)
An external address
![]() $\underline {s}$
is a sequence
$\underline {s}$
is a sequence
![]() $\underline {s}=s_1 s_2 s_3\ldots $
over the integers. We denote by
$\underline {s}=s_1 s_2 s_3\ldots $
over the integers. We denote by
![]() $\mathcal {S}=\mathbb {Z}^{\mathbb {N}}$
the space of all external addresses and by
$\mathcal {S}=\mathbb {Z}^{\mathbb {N}}$
the space of all external addresses and by
![]() $\sigma \colon \mathcal {S}\to \mathcal {S}$
,
$\sigma \colon \mathcal {S}\to \mathcal {S}$
,
![]() $\sigma (s_1 s_2 s_3\ldots )=s_2 s_3\ldots $
the left shift map.
$\sigma (s_1 s_2 s_3\ldots )=s_2 s_3\ldots $
the left shift map.
The shift space
![]() $\mathcal {S}$
can be totally ordered using lexicographic order (for
$\mathcal {S}$
can be totally ordered using lexicographic order (for
![]() $\underline {s},\underline {t}\in \mathcal {S}$
, we write
$\underline {s},\underline {t}\in \mathcal {S}$
, we write
![]() $\underline {s}< \underline {t}$
if and only if
$\underline {s}< \underline {t}$
if and only if
![]() $\underline {s}=s_1 s_2 s_3\ldots $
and
$\underline {s}=s_1 s_2 s_3\ldots $
and
![]() $\underline {t}=t_1 t_2 t_3\ldots $
have a k so that
$\underline {t}=t_1 t_2 t_3\ldots $
have a k so that
![]() $s_1=t_1$
, … ,
$s_1=t_1$
, … ,
![]() $s_k=t_k$
and
$s_k=t_k$
and
![]() $s_{k+1}<t_{k+1}$
). The lexicographic order defines the order topology on
$s_{k+1}<t_{k+1}$
). The lexicographic order defines the order topology on
![]() $\mathcal {S}$
. Any total order induces a cyclic order on the same set: for distinct
$\mathcal {S}$
. Any total order induces a cyclic order on the same set: for distinct
![]() $\underline {s},\underline {t},\underline {u}\in \mathcal {S}$
, we write
$\underline {s},\underline {t},\underline {u}\in \mathcal {S}$
, we write
We write
![]() $(\underline {s},\underline {t})$
for the open interval between
$(\underline {s},\underline {t})$
for the open interval between
![]() $\underline {s}$
and
$\underline {s}$
and
![]() $\underline {t}$
with respect to the cyclic order on
$\underline {t}$
with respect to the cyclic order on
![]() $\mathcal {S}$
, that is, we have
$\mathcal {S}$
, that is, we have
![]() $\underline {u}\in (\underline {s},\underline {t})$
if and only if
$\underline {u}\in (\underline {s},\underline {t})$
if and only if
![]() $\underline {s}\prec \underline {u}\prec \underline {t}$
.
$\underline {s}\prec \underline {u}\prec \underline {t}$
.
The following theorem is a weak version of the classification result proved in [Reference Schleicher and ZimmerSZ1], but it is all we need for this work.
Proposition 2.4. (The escaping set of a post-singularly finite exponential map)
Let
![]() $E_{\lambda }$
be a psf exponential map. Then every escaping point either lies on a unique dynamic ray or is the landing point of a unique ray. In particular, distinct dynamic rays are disjoint.
$E_{\lambda }$
be a psf exponential map. Then every escaping point either lies on a unique dynamic ray or is the landing point of a unique ray. In particular, distinct dynamic rays are disjoint.
We can assign to each (pre-)periodic external address
![]() $\underline {s}$
a dynamic ray
$\underline {s}$
a dynamic ray
![]() $g_{\underline {s}}\colon (0,\infty )\to \mathbb {C}$
in such a way that
$g_{\underline {s}}\colon (0,\infty )\to \mathbb {C}$
in such a way that
where
![]() $F(t)=e^t-1$
, and so that
$F(t)=e^t-1$
, and so that
Here, we chose the branch of the logarithm for which
![]() $\operatorname {Im} \log \lambda \in (-\pi ,\pi ]$
.
$\operatorname {Im} \log \lambda \in (-\pi ,\pi ]$
.
Remark 2.5. Note that the landing point of a dynamic ray can be an escaping point; in this case, there cannot be another dynamic ray with the same landing point. In contrast, a non-escaping point can be the landing point of several dynamic rays. Indeed, (pre-)periodic rays landing together play an important role in this paper.
We partition the complex plane into horizontal strips of the form
with
![]() $k\in \mathbb {Z}$
. This partition is called the static partition for
$k\in \mathbb {Z}$
. This partition is called the static partition for
![]() $E_{\lambda }$
.
$E_{\lambda }$
.
Equation (1) implies that every dynamic ray is, for all sufficiently large potentials t, contained in a single sector of the static partition, that is, there exists a
![]() $k\in \mathbb {Z}$
such that
$k\in \mathbb {Z}$
such that
![]() $g(t)\in S_k$
for t large enough.
$g(t)\in S_k$
for t large enough.
Definition 2.6. (External address of a dynamic ray)
Let g be a dynamic ray for a psf exponential map
![]() $E_{\lambda }$
. The external address
$E_{\lambda }$
. The external address
![]() $\text {Ad}(g)=s_1 s_2\ldots \in \mathcal {S}$
of the dynamic ray g is the unique external address such that for every
$\text {Ad}(g)=s_1 s_2\ldots \in \mathcal {S}$
of the dynamic ray g is the unique external address such that for every
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
Remark 2.7. We see that
![]() $\text {Ad}(g_{\underline {t}})=\underline {t}$
for the dynamic rays
$\text {Ad}(g_{\underline {t}})=\underline {t}$
for the dynamic rays
![]() $g_{\underline {t}}$
defined in Proposition 2.4. Different dynamic rays have different external addresses (as follows from the full version of the classification result in [Reference Schleicher and ZimmerSZ1]), but not every external address is the address of a dynamic ray. A sequence
$g_{\underline {t}}$
defined in Proposition 2.4. Different dynamic rays have different external addresses (as follows from the full version of the classification result in [Reference Schleicher and ZimmerSZ1]), but not every external address is the address of a dynamic ray. A sequence
![]() $\underline {s}\in \mathcal {S}$
occurs as the external address of a dynamic ray if and only if it is exponentially bounded (see [Reference Schleicher and ZimmerSZ1, Definition 4.1 and Theorem 4.2]).
$\underline {s}\in \mathcal {S}$
occurs as the external address of a dynamic ray if and only if it is exponentially bounded (see [Reference Schleicher and ZimmerSZ1, Definition 4.1 and Theorem 4.2]).
Because dynamic rays are disjoint and converge to
![]() $\infty $
in a controlled way, as described in (1), they have a well-defined vertical order, defined as follows.
$\infty $
in a controlled way, as described in (1), they have a well-defined vertical order, defined as follows.
Definition 2.8. (Vertical order of dynamic rays)
Let g and
![]() $g'$
be two dynamic rays of
$g'$
be two dynamic rays of
![]() $E_{\lambda }$
. Then for sufficiently large
$E_{\lambda }$
. Then for sufficiently large
![]() $\xi>0$
, the ray g disconnects the right half-plane
$\xi>0$
, the ray g disconnects the right half-plane
![]() $\{z\in \mathbb {C}\colon \operatorname {Re}(z)>\xi \}$
into exactly two unbounded parts (plus possibly some bounded ones), and the curve
$\{z\in \mathbb {C}\colon \operatorname {Re}(z)>\xi \}$
into exactly two unbounded parts (plus possibly some bounded ones), and the curve
![]() $g'(t)$
must be contained in a single one of them for all sufficiently large t. We say that g lies above
$g'(t)$
must be contained in a single one of them for all sufficiently large t. We say that g lies above
![]() $g'$
if
$g'$
if
![]() $g'$
(for large potentials) is contained in the lower of these two unbounded components, and write
$g'$
(for large potentials) is contained in the lower of these two unbounded components, and write
![]() $g>g'$
; otherwise we say that g lies below
$g>g'$
; otherwise we say that g lies below
![]() $g'$
and write
$g'$
and write
![]() $g<g'$
.
$g<g'$
.
It follows easily from the mapping properties of the exponential map that the vertical order of dynamic rays coincides with the lexicographical order of their external addresses (see [Reference Förster and SchleicherFS, Lemma 3.9]).
Lemma 2.9. (Order of rays and external addresses)
For any two dynamic rays
![]() $g_{\underline {t}}$
and
$g_{\underline {t}}$
and
![]() $g_{\underline {t}'}$
of
$g_{\underline {t}'}$
of
![]() $E_{\lambda }$
, the ray
$E_{\lambda }$
, the ray
![]() $g_{\underline {t}}$
lies above
$g_{\underline {t}}$
lies above
![]() $g_{\underline {t}'}$
if and only if
$g_{\underline {t}'}$
if and only if
![]() $\underline {t}> \underline {t}'$
in lexicographic ordering.
$\underline {t}> \underline {t}'$
in lexicographic ordering.
As described above for the space of external addresses, the linear order induces a cyclic order on the set of dynamic rays; we write
![]() $g\prec g'\prec g''$
if
$g\prec g'\prec g''$
if
![]() $g'$
lies between g and
$g'$
lies between g and
![]() $g''$
in this cyclic order. The map assigning to each ray its external address preserves the cyclic order (as it preserves the linear order inducing it).
$g''$
in this cyclic order. The map assigning to each ray its external address preserves the cyclic order (as it preserves the linear order inducing it).
For the purposes of this paper, we are most interested in (pre-)periodic dynamic rays and their landing behavior (compare Definition 2.2). It was shown in [Reference Schleicher and ZimmerSZ2, Theorem 3.2] that every (pre-)periodic dynamic ray of a psf exponential map that is not eventually mapped onto a ray landing at the singular value
![]() $0$
lands at a (pre-)periodic point. Conversely, every (pre-)periodic point is the landing point of at least one (pre-)periodic dynamic ray by [Reference Schleicher and ZimmerSZ2, Theorem 5.3]. This result is in analogy to the Douady–Hubbard landing theorem for polynomials.
$0$
lands at a (pre-)periodic point. Conversely, every (pre-)periodic point is the landing point of at least one (pre-)periodic dynamic ray by [Reference Schleicher and ZimmerSZ2, Theorem 5.3]. This result is in analogy to the Douady–Hubbard landing theorem for polynomials.
Theorem 2.10. (A landing theorem [Reference Schleicher and ZimmerSZ2])
For every post-singularly finite exponential map, every periodic or pre-periodic point is the landing point of at least one and at most finitely many periodic, respectively pre-periodic, dynamic rays. Rays landing at the same point have the same pre-period and period.
We construct a partition of the plane that allows us to describe in combinatorial terms which dynamic rays are landing together: Choose a pre-periodic dynamic ray
![]() $g_{\underline {s}}$
landing at
$g_{\underline {s}}$
landing at
![]() $0$
. The pre-image
$0$
. The pre-image
![]() $E_{\lambda }^{-1}(\operatorname {\mathrm {Tr}}(g_{\underline {s}}))$
consists of countably many disjoint simple curves which are translations of each other by integer multiples of
$E_{\lambda }^{-1}(\operatorname {\mathrm {Tr}}(g_{\underline {s}}))$
consists of countably many disjoint simple curves which are translations of each other by integer multiples of
![]() $2\pi i$
. Furthermore, if g is any lift of
$2\pi i$
. Furthermore, if g is any lift of
![]() $g_{\underline {s}}$
by
$g_{\underline {s}}$
by
![]() $E_{\lambda }$
, then we have
$E_{\lambda }$
, then we have
by the mapping properties of exponential maps.
We define a sector to be a connected component of
![]() $\mathbb {C}\setminus E_{\lambda }^{-1}(\operatorname {\mathrm {Tr}}(g_{\underline {s}}))$
. These sectors partition
$\mathbb {C}\setminus E_{\lambda }^{-1}(\operatorname {\mathrm {Tr}}(g_{\underline {s}}))$
. These sectors partition
![]() $\mathbb {C}$
so that the sector boundaries are exactly the pre-images of the ray
$\mathbb {C}$
so that the sector boundaries are exactly the pre-images of the ray
![]() $g_{\underline {s}}$
.
$g_{\underline {s}}$
.
Because distinct dynamic rays are disjoint, there is a unique sector
![]() $D_0$
containing the ray
$D_0$
containing the ray
![]() $g_{\underline {s}}$
and its landing point
$g_{\underline {s}}$
and its landing point
![]() $0$
. For
$0$
. For
![]() $k\in \mathbb {Z}$
, the sector obtained by translating
$k\in \mathbb {Z}$
, the sector obtained by translating
![]() $D_0$
by
$D_0$
by
![]() $2k\pi i$
is called
$2k\pi i$
is called
![]() $D_k$
. Observe that for all
$D_k$
. Observe that for all
![]() $k\in \mathbb {Z}$
, the restriction
$k\in \mathbb {Z}$
, the restriction
![]() $E_{\lambda }\colon D_k\to \mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {s}})\cup \{0\})$
is biholomorphic. We call
$E_{\lambda }\colon D_k\to \mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {s}})\cup \{0\})$
is biholomorphic. We call
![]() $\mathcal {D}:=\bigcup _{k\in \mathbb {Z}}\{D_k\}$
the dynamical partition for
$\mathcal {D}:=\bigcup _{k\in \mathbb {Z}}\{D_k\}$
the dynamical partition for
![]() $E_{\lambda }$
with respect to
$E_{\lambda }$
with respect to
![]() $g_{\underline {s}}$
and we call
$g_{\underline {s}}$
and we call
![]() $\partial \mathcal {D}:=E_{\lambda }^{-1}(\operatorname {\mathrm {Tr}}(g_{\underline {s}}))$
the boundary of the partition
$\partial \mathcal {D}:=E_{\lambda }^{-1}(\operatorname {\mathrm {Tr}}(g_{\underline {s}}))$
the boundary of the partition
![]() $\mathcal {D}$
. Note that
$\mathcal {D}$
. Note that
![]() $\mathcal {D}$
is a collection of subsets of
$\mathcal {D}$
is a collection of subsets of
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and
![]() $\partial \mathcal {D}\subset \mathbb {C}$
.
$\partial \mathcal {D}\subset \mathbb {C}$
.
As dynamic rays are parameterized by external addresses, the dynamical partition can also be constructed on the level of external addresses. Consider again the shift space
![]() $\mathcal {S}$
endowed with the lexicographic order. In the following, terms like
$\mathcal {S}$
endowed with the lexicographic order. In the following, terms like
![]() $t_0\underline {t}\in \mathcal {S}$
with
$t_0\underline {t}\in \mathcal {S}$
with
![]() $t_0\in \mathbb {Z}$
and
$t_0\in \mathbb {Z}$
and
![]() $\underline {t}\in \mathcal {S}$
will denote concatenation of an integer and an external address.
$\underline {t}\in \mathcal {S}$
will denote concatenation of an integer and an external address.
We start with the external address
![]() $\underline {s}=s_1 s_2\ldots $
of the dynamic ray
$\underline {s}=s_1 s_2\ldots $
of the dynamic ray
![]() $g_{\underline {s}}$
. This address is not constant, so we either have
$g_{\underline {s}}$
. This address is not constant, so we either have
![]() $\underline {s}\in ((s_1-1)\underline {s}, s_1\underline {s})$
or
$\underline {s}\in ((s_1-1)\underline {s}, s_1\underline {s})$
or
![]() $\underline {s}\in (s_1\underline {s}, (s_1+1)\underline {s})$
. Denote the interval containing
$\underline {s}\in (s_1\underline {s}, (s_1+1)\underline {s})$
. Denote the interval containing
![]() $\underline {s}$
by
$\underline {s}$
by
![]() $I_0$
. For all
$I_0$
. For all
![]() $k\in \mathbb {Z}$
, we define the interval
$k\in \mathbb {Z}$
, we define the interval
Observe that
![]() $\mathcal {I}:=\bigcup _{k\in \mathbb {Z}} \{I_{k}\}$
is a partition of the shift space
$\mathcal {I}:=\bigcup _{k\in \mathbb {Z}} \{I_{k}\}$
is a partition of the shift space
![]() $\mathcal {S}$
, which we call the dynamical partition of
$\mathcal {S}$
, which we call the dynamical partition of
![]() $\mathcal {S}$
with respect to
$\mathcal {S}$
with respect to
![]() $\underline {s}$
. We denote by
$\underline {s}$
. We denote by
![]() $\partial \mathcal {I}:=\sigma ^{-1}(\underline {s})\subset \mathcal {S}$
the boundary of the partition
$\partial \mathcal {I}:=\sigma ^{-1}(\underline {s})\subset \mathcal {S}$
the boundary of the partition
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
It follows from Lemma 2.9 that a dynamic ray g is contained in the sector
![]() $D_k$
of the dynamical partition
$D_k$
of the dynamical partition
![]() $\mathcal {D}$
of the complex plane if and only if its address
$\mathcal {D}$
of the complex plane if and only if its address
![]() $\text {Ad}(g)\in \mathcal {S}$
is contained in the sector
$\text {Ad}(g)\in \mathcal {S}$
is contained in the sector
![]() $I_k$
of the dynamical partition of the shift space. Recording the sectors in
$I_k$
of the dynamical partition of the shift space. Recording the sectors in
![]() $\mathcal {D}$
to which a point in the plane is mapped under iteration of
$\mathcal {D}$
to which a point in the plane is mapped under iteration of
![]() $E_{\lambda }$
yields so-called itineraries. The same applies to the partition
$E_{\lambda }$
yields so-called itineraries. The same applies to the partition
![]() $\mathcal {I}$
of the shift space.
$\mathcal {I}$
of the shift space.
Definition 2.11. (Itineraries of external addresses and the kneading sequence)
Let
![]() $\star $
be a formal symbol not contained in
$\star $
be a formal symbol not contained in
![]() $\mathbb {Z}$
and let
$\mathbb {Z}$
and let
![]() $\underline {t}\in \mathcal {S}$
be an external address. Then the itinerary
$\underline {t}\in \mathcal {S}$
be an external address. Then the itinerary
![]() $\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})$
of
$\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})$
of
![]() $\underline {t}$
with respect to
$\underline {t}$
with respect to
![]() $\underline {s}$
is the unique sequence
$\underline {s}$
is the unique sequence
![]() $\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})=\mathtt {\underline {t}}=\mathtt {t}_1\mathtt {t}_2\ldots \in (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
such that
$\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})=\mathtt {\underline {t}}=\mathtt {t}_1\mathtt {t}_2\ldots \in (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
such that
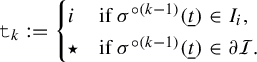 $$ \begin{align*} \mathtt{t}_k:= \begin{cases} i & \text{if } \sigma^{\circ(k-1)}(\underline{t})\in I_i,\\ \star & \text{if } \sigma^{\circ(k-1)}(\underline{t})\in \partial\mathcal{I}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathtt{t}_k:= \begin{cases} i & \text{if } \sigma^{\circ(k-1)}(\underline{t})\in I_i,\\ \star & \text{if } \sigma^{\circ(k-1)}(\underline{t})\in \partial\mathcal{I}. \end{cases} \end{align*} $$
We call the itinerary
![]() $\nu :=\operatorname {\mathrm {It}}(\underline {s}~\vert ~\underline {s})$
the kneading sequence of the external address
$\nu :=\operatorname {\mathrm {It}}(\underline {s}~\vert ~\underline {s})$
the kneading sequence of the external address
![]() $\underline {s}$
.
$\underline {s}$
.
Definition 2.12. (Itineraries of points and dynamic rays)
Let
![]() $\star $
be a formal symbol not contained in
$\star $
be a formal symbol not contained in
![]() $\mathbb {Z}$
. For a point
$\mathbb {Z}$
. For a point
![]() $z\in \mathbb {C}$
, we define the itinerary of z with respect to
$z\in \mathbb {C}$
, we define the itinerary of z with respect to
![]() $\mathcal {D}$
to be the sequence
$\mathcal {D}$
to be the sequence
![]() $\operatorname {\mathrm {It}}(z~\vert ~\mathcal {D})=\mathtt {\underline {t}}=\mathtt {t}_1\mathtt {t}_2\ldots \in (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
such that
$\operatorname {\mathrm {It}}(z~\vert ~\mathcal {D})=\mathtt {\underline {t}}=\mathtt {t}_1\mathtt {t}_2\ldots \in (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
such that
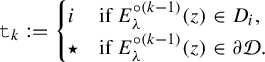 $$ \begin{align*} \mathtt{t}_k:= \begin{cases} i & \text{if } E_{\lambda}^{\circ (k-1)}(z)\in D_i,\\ \star & \text{if } E_{\lambda}^{\circ (k-1)}(z)\in \partial\mathcal{D}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathtt{t}_k:= \begin{cases} i & \text{if } E_{\lambda}^{\circ (k-1)}(z)\in D_i,\\ \star & \text{if } E_{\lambda}^{\circ (k-1)}(z)\in \partial\mathcal{D}. \end{cases} \end{align*} $$
Let g be a dynamic ray of
![]() $E_{\lambda }$
. As distinct dynamic rays do not intersect and the partition boundary
$E_{\lambda }$
. As distinct dynamic rays do not intersect and the partition boundary
![]() $\partial \mathcal {D}$
consists of rays, every iterate of g is either fully contained in a single sector of the dynamical partition or part of the partition boundary. Therefore, all points on g have equal itineraries and we set
$\partial \mathcal {D}$
consists of rays, every iterate of g is either fully contained in a single sector of the dynamical partition or part of the partition boundary. Therefore, all points on g have equal itineraries and we set
![]() $\operatorname {\mathrm {It}}(g~\vert ~\mathcal {D}):=\operatorname {\mathrm {It}}(w~\vert ~\mathcal {D})$
for an arbitrary point
$\operatorname {\mathrm {It}}(g~\vert ~\mathcal {D}):=\operatorname {\mathrm {It}}(w~\vert ~\mathcal {D})$
for an arbitrary point
![]() $w\in \operatorname {\mathrm {Tr}}(g)$
.
$w\in \operatorname {\mathrm {Tr}}(g)$
.
Itineraries are written in a different font to distinguish them from external addresses. Observe that the itinerary of a (pre-)periodic point is itself (pre-)periodic. Furthermore, it does not contain the symbol
![]() $\star $
because
$\star $
because
![]() $\partial \mathcal {D}$
consists of escaping points.
$\partial \mathcal {D}$
consists of escaping points.
The following proposition describes the landing behavior of (pre-)periodic dynamic rays in terms of itineraries. It is crucial for the construction of homotopy Hubbard trees for exponential maps. A proof can be found in [Reference Schleicher and ZimmerSZ2, Lemma 5.2 and Theorem 5.3].
Proposition 2.13. (Landing behavior of (pre-)periodic rays [Reference Schleicher and ZimmerSZ2])
Let
![]() $E_{\lambda }$
be a psf, let
$E_{\lambda }$
be a psf, let
![]() $\underline {s}$
be the external address of a dynamic ray landing at the singular value, and let
$\underline {s}$
be the external address of a dynamic ray landing at the singular value, and let
![]() $\mathcal {D}$
be the corresponding dynamical partition; denote the kneading sequence of
$\mathcal {D}$
be the corresponding dynamical partition; denote the kneading sequence of
![]() $\underline {s}$
by
$\underline {s}$
by
![]() $\nu $
.
$\nu $
.
The map
![]() $z\mapsto \operatorname {\mathrm {It}}(z~\vert ~\mathcal {D})$
is a bijection between (pre-)periodic points and (pre-)periodic itineraries
$z\mapsto \operatorname {\mathrm {It}}(z~\vert ~\mathcal {D})$
is a bijection between (pre-)periodic points and (pre-)periodic itineraries
![]() $\mathtt {\underline {t}}\in \mathbb {Z}^{\mathbb {N}}$
satisfying
$\mathtt {\underline {t}}\in \mathbb {Z}^{\mathbb {N}}$
satisfying
![]() $\sigma ^{\circ n}(\mathtt {\underline {t}})\neq \nu $
for all
$\sigma ^{\circ n}(\mathtt {\underline {t}})\neq \nu $
for all
![]() $n\in \mathbb {N}$
. The (pre-)periodic ray
$n\in \mathbb {N}$
. The (pre-)periodic ray
![]() $g_{\underline {t}}$
lands at the (pre-)periodic point z if and only if
$g_{\underline {t}}$
lands at the (pre-)periodic point z if and only if
![]() $\operatorname {\mathrm {It}}(z~\vert ~\mathcal {D})=\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})$
.
$\operatorname {\mathrm {It}}(z~\vert ~\mathcal {D})=\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})$
.
One of the main goals of this paper is to classify post-singularly finite exponential maps in terms of their abstract Hubbard trees. A different classification of psf exponential maps has already been obtained in [Reference Laubner, Schleicher and VicolLSV, Theorems 2.6 and 2.7].
Theorem 2.14. (Classification of post-singularly finite exponential maps [Reference Laubner, Schleicher and VicolLSV])
For every pre-periodic external address
![]() $\underline {s}$
starting with the entry
$\underline {s}$
starting with the entry
![]() $0$
, there is a unique post-singularly finite exponential map such that the dynamic ray at external address
$0$
, there is a unique post-singularly finite exponential map such that the dynamic ray at external address
![]() $\underline {s}$
lands at the singular value.
$\underline {s}$
lands at the singular value.
Every post-singularly finite exponential map is associated in this way to a positive finite number of pre-periodic external addresses starting with
![]() $0$
. Two such external addresses
$0$
. Two such external addresses
![]() $\underline {s}$
and
$\underline {s}$
and
![]() $\underline {s}'$
are associated to the same exponential map if and only if
$\underline {s}'$
are associated to the same exponential map if and only if
![]() $\operatorname {\mathrm {It}}(\underline {s}'~\vert ~\underline {s})=\operatorname {\mathrm {It}}(\underline {s}~\vert ~\underline {s})$
.
$\operatorname {\mathrm {It}}(\underline {s}'~\vert ~\underline {s})=\operatorname {\mathrm {It}}(\underline {s}~\vert ~\underline {s})$
.
We do not use this result, neither for the construction of homotopy Hubbard trees for exponential maps nor in the proof of our own classification result. Still, it is a nice insight to have in mind during the upcoming constructions.
Convention 2.15. Let
![]() $E_{\lambda }$
be a post-singularly finite exponential map. For the rest of the paper,
$E_{\lambda }$
be a post-singularly finite exponential map. For the rest of the paper,
![]() $\underline {s}$
will always denote the external address of a dynamic ray landing at the singular value and
$\underline {s}$
will always denote the external address of a dynamic ray landing at the singular value and
![]() $\nu $
will denote its kneading sequence.
$\nu $
will denote its kneading sequence.
3 Homotopy Hubbard trees
Hubbard trees were defined for polynomials over thirty years ago in [Reference Douady and HubbardDH1]. We give here a more conceptual but equivalent definition of Hubbard trees, which has a better chance to be generalized to the case of exponential maps than the original one given in [Reference Douady and HubbardDH1] (which uses the concept of filled-in Julia sets). To avoid difficulties arising from unnecessary generality, we do not give the most general definition, but a definition valid for unicritical polynomials (polynomials with only one critical point in the complex plane) with pre-periodic critical value. This makes sense from a conceptual viewpoint as exponential maps are a dynamical limit of unicritical polynomials [Reference Bodelón, Devaney, Hayes, Roberts, Goldberg and HubbardDGH] and for post-singularly finite exponential maps, the unique singular value is pre-periodic.
Let us make the concept of an embedded tree precise. Our definition differs from the standard definition (based on a topological quotient) in the case of infinite trees: infinite trees occur naturally as part of our construction and the topology of these trees at vertices of infinite degree deviates from the usual quotient topology.
Definition 3.1. (Embedded graphs and trees)
A topological space G is called a topological graph if it is homeomorphic to a space
of disjoint copies of the unit interval
![]() $[0, 1]$
, where I is some index set (for our purposes, we may restrict to countable index sets) and
$[0, 1]$
, where I is some index set (for our purposes, we may restrict to countable index sets) and
![]() $\sim $
is an equivalence relation identifying some of the endpoints of the intervals
$\sim $
is an equivalence relation identifying some of the endpoints of the intervals
![]() $[0^{(i)}, 1^{(i)}]$
.
$[0^{(i)}, 1^{(i)}]$
.
Away from equivalence classes of infinite cardinality, we define the topology on X to be the usual quotient topology. In particular, if I is finite, we equip X with the usual quotient topology.
If
![]() $x\in X$
is a vertex of infinite degree, that is, an equivalence class of infinite cardinality, there are index sets
$x\in X$
is a vertex of infinite degree, that is, an equivalence class of infinite cardinality, there are index sets
![]() $I_0, I_1\subset I$
, at least one of which is infinite, such that
$I_0, I_1\subset I$
, at least one of which is infinite, such that
![]() $0^{(i)}\in x$
if and only if
$0^{(i)}\in x$
if and only if
![]() $i\in I_0$
and
$i\in I_0$
and
![]() $1^{(i)}\in x$
if and only if
$1^{(i)}\in x$
if and only if
![]() $i\in I_1$
. For all
$i\in I_1$
. For all
![]() $0 < \epsilon < 1$
, we set
$0 < \epsilon < 1$
, we set
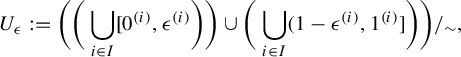 $$ \begin{align*} U_\epsilon := \bigg(\bigg(\bigcup_{i\in I} [0^{(i)}, \epsilon^{(i)}\bigg)\bigg)\cup \bigg(\bigcup_{i\in I} (1-\epsilon^{(i)}, 1^{(i)}] \bigg)\bigg)/_\sim,\end{align*} $$
$$ \begin{align*} U_\epsilon := \bigg(\bigg(\bigcup_{i\in I} [0^{(i)}, \epsilon^{(i)}\bigg)\bigg)\cup \bigg(\bigcup_{i\in I} (1-\epsilon^{(i)}, 1^{(i)}] \bigg)\bigg)/_\sim,\end{align*} $$
and define
![]() $\{U_\epsilon \}_{0<\epsilon <1}$
to be a neighborhood basis of x in X.
$\{U_\epsilon \}_{0<\epsilon <1}$
to be a neighborhood basis of x in X.
We call G finite if the index set I may be chosen to be finite. The topological graph G is called a topological tree if it is connected and has trivial fundamental group.
Definition 3.2. (Branch and endpoints in embedded trees)
A branch of the topological tree H at the point
![]() $p\in H$
is the closure of a connected component of
$p\in H$
is the closure of a connected component of
![]() $H\setminus \{p\}$
. We denote the number of branches of H at p by
$H\setminus \{p\}$
. We denote the number of branches of H at p by
![]() $\text {deg}_H(p)$
and call p a branch point of H if
$\text {deg}_H(p)$
and call p a branch point of H if
![]() $\text {deg}_H(p)\geq 3$
. If
$\text {deg}_H(p)\geq 3$
. If
![]() $\text {deg}_H(p)=1$
, we call p an endpoint of H.
$\text {deg}_H(p)=1$
, we call p an endpoint of H.
Definition 3.3. (Hubbard trees for pre-periodic unicritical polynomials)
Let p be a post-critically finite unicritical polynomial with pre-periodic critical value. The Hubbard tree
![]() $H\subset \mathbb {C}$
of p is the unique finite embedded tree such that:
$H\subset \mathbb {C}$
of p is the unique finite embedded tree such that:
-
•
 $P(p)\subset H$
, that is, the forward orbit of every critical point of p is contained in the tree;
$P(p)\subset H$
, that is, the forward orbit of every critical point of p is contained in the tree; -
• all endpoints of H are contained in
 $P(p)$
; and
$P(p)$
; and -
•
 $p(H)\subset H$
, that is, H is forward invariant under the dynamics of p.
$p(H)\subset H$
, that is, H is forward invariant under the dynamics of p.
The naive way to generalize this definition to the case of exponential maps fails because of the existence of an asymptotic value.
Theorem 3.4. (Hubbard trees of exponential maps must contain escaping points)
Let
![]() $E_{\lambda }$
be a post-singularly finite exponential map. There does not exist a finite embedded tree
$E_{\lambda }$
be a post-singularly finite exponential map. There does not exist a finite embedded tree
![]() $H\subset \mathbb {C}$
that is forward invariant under the dynamics of
$H\subset \mathbb {C}$
that is forward invariant under the dynamics of
![]() $E_{\lambda }$
and contains
$E_{\lambda }$
and contains
![]() $P(E_{\lambda })$
.
$P(E_{\lambda })$
.
Proof Let
![]() $\underline {s}$
be the external address of a dynamic ray landing at the singular value
$\underline {s}$
be the external address of a dynamic ray landing at the singular value
![]() $0$
and let
$0$
and let
![]() $\mathcal {D}$
be the dynamical partition for
$\mathcal {D}$
be the dynamical partition for
![]() $E_{\lambda }$
with respect to
$E_{\lambda }$
with respect to
![]() $g_{\underline {s}}$
. Furthermore, let
$g_{\underline {s}}$
. Furthermore, let
![]() $p,q\in H$
,
$p,q\in H$
,
![]() $p\neq q$
, be arbitrary points of well-defined and different itineraries with respect to
$p\neq q$
, be arbitrary points of well-defined and different itineraries with respect to
![]() $\mathcal {D}$
. For example, one can easily verify that there are two points on the forward orbit of
$\mathcal {D}$
. For example, one can easily verify that there are two points on the forward orbit of
![]() $0$
which differ by a multiple of
$0$
which differ by a multiple of
![]() $2\pi i$
and hence lie in different sectors of the dynamical partition
$2\pi i$
and hence lie in different sectors of the dynamical partition
![]() $\mathcal {D}$
, so one could take p and q to be those two points. Because H is a tree, there is a unique arc
$\mathcal {D}$
, so one could take p and q to be those two points. Because H is a tree, there is a unique arc
![]() $\gamma \colon [0,1]\to H$
connecting p and q. Because H is forward-invariant, for every
$\gamma \colon [0,1]\to H$
connecting p and q. Because H is forward-invariant, for every
![]() $n\geq 0$
, the points
$n\geq 0$
, the points
![]() $E_{\lambda }^{\circ n}(p)$
and
$E_{\lambda }^{\circ n}(p)$
and
![]() $E_{\lambda }^{\circ n}(q)$
are connected within H by
$E_{\lambda }^{\circ n}(q)$
are connected within H by
![]() $E_{\lambda }^{\circ n}(\gamma )$
. By hypothesis, for some
$E_{\lambda }^{\circ n}(\gamma )$
. By hypothesis, for some
![]() $k\in \mathbb {N}$
, the points
$k\in \mathbb {N}$
, the points
![]() $E_{\lambda }^{\circ k}(p)$
and
$E_{\lambda }^{\circ k}(p)$
and
![]() $E_{\lambda }^{\circ k}(q)$
lie in different sectors of the dynamical partition, thus, by continuity,
$E_{\lambda }^{\circ k}(q)$
lie in different sectors of the dynamical partition, thus, by continuity,
![]() $E_{\lambda }^{\circ k}(\gamma )$
crosses the partition boundary and contains an escaping point, which contradicts the forward invariance of H.
$E_{\lambda }^{\circ k}(\gamma )$
crosses the partition boundary and contains an escaping point, which contradicts the forward invariance of H.
The idea that leads us to a meaningful definition of Hubbard trees for exponential maps is to relax the invariance condition: we do not require a Hubbard tree to be exactly forward invariant, but only invariant up to homotopy relative to the post-singular set. Note that this relaxation is not only necessary (because there is no exactly invariant tree), but also natural from the point of view of Thurston’s theory: an exponential Hubbard tree should determine a psf exponential map up to Thurston equivalence, and the Thurston equivalence class of a map is invariant under homotopies relative to the post-singular set in the domain and co-domain of the map (see Definition 6.4).
Because homotopies rel
![]() $P(E_{\lambda })$
cannot be pushed forward by
$P(E_{\lambda })$
cannot be pushed forward by
![]() $E_{\lambda }$
(because of the existence of non-post-singular pre-images of post-singular points), the right way to formulate the forward invariance condition is through backwards iteration. We want to say that the pre-image
$E_{\lambda }$
(because of the existence of non-post-singular pre-images of post-singular points), the right way to formulate the forward invariance condition is through backwards iteration. We want to say that the pre-image
![]() $E_{\lambda }^{-1}(H)$
of a Hubbard tree H contains H up to homotopy rel
$E_{\lambda }^{-1}(H)$
of a Hubbard tree H contains H up to homotopy rel
![]() $P(E_{\lambda })$
. This statement bears a problem. The pre-image
$P(E_{\lambda })$
. This statement bears a problem. The pre-image
![]() $E_{\lambda }^{-1}(H)$
is disconnected because H contains the singular value
$E_{\lambda }^{-1}(H)$
is disconnected because H contains the singular value
![]() $0$
. Different connected components of
$0$
. Different connected components of
![]() $E_{\lambda }^{-1}(H)$
contain post-singular points which are, by definition, contained in H and are not allowed to move during the homotopy. Hence, by connectedness, H cannot be homotoped into its pre-image
$E_{\lambda }^{-1}(H)$
contain post-singular points which are, by definition, contained in H and are not allowed to move during the homotopy. Hence, by connectedness, H cannot be homotoped into its pre-image
![]() $E_{\lambda }^{-1}(H)$
. By adding a pre-image
$E_{\lambda }^{-1}(H)$
. By adding a pre-image
![]() $-\infty $
of
$-\infty $
of
![]() $0$
to the complex plane, the pre- image of H becomes connected and in fact becomes an (infinite) embedded tree, so it makes sense to require that H can be homotoped into
$0$
to the complex plane, the pre- image of H becomes connected and in fact becomes an (infinite) embedded tree, so it makes sense to require that H can be homotoped into
![]() $E_{\lambda }^{-1}(H)\cup \{-\infty \}$
rel
$E_{\lambda }^{-1}(H)\cup \{-\infty \}$
rel
![]() $P(E_{\lambda })$
in the extended plane.
$P(E_{\lambda })$
in the extended plane.
Let us make this idea precise. Let
![]() $\mathbb {C}_T$
(as a set) be defined as the disjoint union
$\mathbb {C}_T$
(as a set) be defined as the disjoint union
![]() $\mathbb {C}_T:=\mathbb {C}\mathbin {\dot {\cup }}\{-\infty \}$
, where, for now, the point
$\mathbb {C}_T:=\mathbb {C}\mathbin {\dot {\cup }}\{-\infty \}$
, where, for now, the point
![]() $-\infty $
is just an abstract point not contained in the complex plane. We turn
$-\infty $
is just an abstract point not contained in the complex plane. We turn
![]() $\mathbb {C}_T$
into a topological space by choosing a neighborhood basis
$\mathbb {C}_T$
into a topological space by choosing a neighborhood basis
![]() $(V_n)$
of
$(V_n)$
of
![]() $0$
and declaring the sets
$0$
and declaring the sets
![]() $U_n:=E_{\lambda }^{-1}(V_n)\cup \{-\infty \}$
to be a neighborhood basis of
$U_n:=E_{\lambda }^{-1}(V_n)\cup \{-\infty \}$
to be a neighborhood basis of
![]() $\{-\infty \}$
. The extension
$\{-\infty \}$
. The extension
![]() $\widehat {E_{\lambda }}\colon \mathbb {C}_T\to \mathbb {C}$
of
$\widehat {E_{\lambda }}\colon \mathbb {C}_T\to \mathbb {C}$
of
![]() $E_{\lambda }$
defined by
$E_{\lambda }$
defined by
![]() $\widehat {E_{\lambda }}(-\infty ):=0$
is continuous by definition. The completion
$\widehat {E_{\lambda }}(-\infty ):=0$
is continuous by definition. The completion
![]() $\mathbb {C}_T$
of
$\mathbb {C}_T$
of
![]() $\mathbb {C}$
is a special case of a far more general construction of defining a completion of the domain of a holomorphic function by adding all transcendental singularities of its inverse function. See [Reference EremenkoE2] for further information. The extended map
$\mathbb {C}$
is a special case of a far more general construction of defining a completion of the domain of a holomorphic function by adding all transcendental singularities of its inverse function. See [Reference EremenkoE2] for further information. The extended map
![]() $\widehat {E_{\lambda }}$
is not a covering map any more, but we can still lift homeomorphisms and homotopies of the complex plane that fix
$\widehat {E_{\lambda }}$
is not a covering map any more, but we can still lift homeomorphisms and homotopies of the complex plane that fix
![]() $0$
under
$0$
under
![]() $\widehat {E_{\lambda }}$
.
$\widehat {E_{\lambda }}$
.
Lemma 3.5. (Lifting homeomorphisms)
Let
![]() $A\subset \mathbb {C}$
be a set containing
$A\subset \mathbb {C}$
be a set containing
![]() $0$
and
$0$
and
![]() $\varphi \colon \mathbb {C}\to \mathbb {C}$
be a homeomorphism which is homotopic to the identity relative to A. There exists a unique homeomorphism
$\varphi \colon \mathbb {C}\to \mathbb {C}$
be a homeomorphism which is homotopic to the identity relative to A. There exists a unique homeomorphism
![]() $\Phi \colon \mathbb {C}_T\to \mathbb {C}_T$
which is homotopic to the identity relative to
$\Phi \colon \mathbb {C}_T\to \mathbb {C}_T$
which is homotopic to the identity relative to
![]() $\widehat {E_{\lambda }}^{-1}(A)$
such that the diagram
$\widehat {E_{\lambda }}^{-1}(A)$
such that the diagram
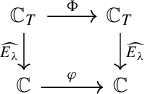
commutes. We call
![]() $\Phi $
the preferred lift of
$\Phi $
the preferred lift of
![]() $\varphi $
. Every homotopy between
$\varphi $
. Every homotopy between
![]() $\varphi $
and
$\varphi $
and
![]() $\text {id}$
rel A lifts to a homotopy between
$\text {id}$
rel A lifts to a homotopy between
![]() $\Phi $
and
$\Phi $
and
![]() $\text {id}$
rel
$\text {id}$
rel
![]() $\widehat {E_{\lambda }}^{-1}(A)$
.
$\widehat {E_{\lambda }}^{-1}(A)$
.
Proof It follows from the homotopy lifting principle that every homotopy between
![]() $\text {id}$
and
$\text {id}$
and
![]() $\varphi $
rel A lifts to a homotopy between
$\varphi $
rel A lifts to a homotopy between
![]() $\text {id}$
and a homeomorphism
$\text {id}$
and a homeomorphism
![]() $\Phi \colon \mathbb {C}\to \mathbb {C}$
relative to
$\Phi \colon \mathbb {C}\to \mathbb {C}$
relative to
![]() $E_{\lambda }^{-1}(A)$
. Both the map
$E_{\lambda }^{-1}(A)$
. Both the map
![]() $\Phi $
and the homotopy between
$\Phi $
and the homotopy between
![]() $\Phi $
and the identity extend continuously to
$\Phi $
and the identity extend continuously to
![]() $\mathbb {C}_T$
and fix
$\mathbb {C}_T$
and fix
![]() $-\infty $
because
$-\infty $
because
![]() $\varphi $
as well as the homotopy between
$\varphi $
as well as the homotopy between
![]() $\varphi $
and the identity fix
$\varphi $
and the identity fix
![]() $0$
.
$0$
.
To state our definition of homotopy Hubbard trees, we need a bit more vocabulary.
Definition 3.6. (Spanned subtrees)
For an embedded tree
![]() $H\subset X$
and a finite subset
$H\subset X$
and a finite subset
![]() $W\subset H$
, we write
$W\subset H$
, we write
![]() $[W]_H$
(or just
$[W]_H$
(or just
![]() $[W]$
) for the smallest subtree of H containing W. We say that H is spanned by W if
$[W]$
) for the smallest subtree of H containing W. We say that H is spanned by W if
![]() $H=[W]$
. Usually, we write
$H=[W]$
. Usually, we write
![]() $[p_1,p_2,\ldots , p_n]_H$
for the smallest subtree containing the points
$[p_1,p_2,\ldots , p_n]_H$
for the smallest subtree containing the points
![]() $p_i\in H$
(omitting the curly brackets).
$p_i\in H$
(omitting the curly brackets).
Assume that
![]() $H\subset \mathbb {C}$
is a finite embedded tree spanned by
$H\subset \mathbb {C}$
is a finite embedded tree spanned by
![]() $P(E_{\lambda })$
. By the mapping properties of exponential maps,
$P(E_{\lambda })$
. By the mapping properties of exponential maps,
![]() $\widehat {E_{\lambda }}^{-1}(H)\subset \mathbb {C}_T$
is an infinite embedded tree where the only point of infinite degree is
$\widehat {E_{\lambda }}^{-1}(H)\subset \mathbb {C}_T$
is an infinite embedded tree where the only point of infinite degree is
![]() $-\infty $
and every branch of
$-\infty $
and every branch of
![]() $\widehat {E_{\lambda }}^{-1}(H)$
at
$\widehat {E_{\lambda }}^{-1}(H)$
at
![]() $-\infty $
is homeomorphic to H. (This step uses our tailored definition of an infinite tree: the topology near the vertex
$-\infty $
is homeomorphic to H. (This step uses our tailored definition of an infinite tree: the topology near the vertex
![]() $-\infty $
is compatible with the extension
$-\infty $
is compatible with the extension
![]() $\mathbb {C}_T$
.)
$\mathbb {C}_T$
.)
As
![]() $P(E_{\lambda })$
is forward invariant, we have
$P(E_{\lambda })$
is forward invariant, we have
![]() $P(E_{\lambda })\subset \widehat {E_{\lambda }}^{-1}(H)$
, and therefore it makes sense to talk about the subtree
$P(E_{\lambda })\subset \widehat {E_{\lambda }}^{-1}(H)$
, and therefore it makes sense to talk about the subtree
![]() $H':=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
of the pre-image tree spanned by
$H':=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
of the pre-image tree spanned by
![]() $P(E_{\lambda })$
. We say that H is invariant up to homotopy rel
$P(E_{\lambda })$
. We say that H is invariant up to homotopy rel
![]() $P(E_{\lambda })$
if
$P(E_{\lambda })$
if
![]() $H'$
is homotopic to H in the extended plane
$H'$
is homotopic to H in the extended plane
![]() $\mathbb {C}_T$
relative to
$\mathbb {C}_T$
relative to
![]() $P(E_{\lambda })$
. Let us make the last statement precise.
$P(E_{\lambda })$
. Let us make the last statement precise.
Definition 3.7. (Relative homotopies of embedded trees)
Given a subset
![]() $A\subset X$
of the space X and two embedded trees
$A\subset X$
of the space X and two embedded trees
![]() $H,H'\subset X$
, we say that H is homotopic to
$H,H'\subset X$
, we say that H is homotopic to
![]() $H'$
relative to (rel) A if there exists a continuous map
$H'$
relative to (rel) A if there exists a continuous map
![]() $I\colon H\times [0,1]\to X$
with the following properties.
$I\colon H\times [0,1]\to X$
with the following properties.
-
•
 $I^0:=I(\cdot ,0)=\text {id}$
and
$I^0:=I(\cdot ,0)=\text {id}$
and
 $I^1:=I(\cdot ,1)\colon H\to H'$
is a homeomorphism.
$I^1:=I(\cdot ,1)\colon H\to H'$
is a homeomorphism. -
• For all
 $p\in H\setminus A$
, we have
$p\in H\setminus A$
, we have
 $I(p,t)\in X\setminus A$
for all
$I(p,t)\in X\setminus A$
for all
 $t\in [0,1]$
.
$t\in [0,1]$
. -
• For all
 $p\in H\cap A$
, the homotopy I is constant on
$p\in H\cap A$
, the homotopy I is constant on
 $\{p\}\times [0,1]$
.
$\{p\}\times [0,1]$
.
As one might expect, this defines an equivalence relation: if two embedded trees H and
![]() $H'$
are homotopic rel A through
$H'$
are homotopic rel A through
![]() $I\colon H\times [0,1]\to X$
, then also
$I\colon H\times [0,1]\to X$
, then also
![]() $H'$
and H are homotopic rel A through the reversed homotopy
$H'$
and H are homotopic rel A through the reversed homotopy
![]() $\overline {I}\colon H'\times [0,1]\to X$
,
$\overline {I}\colon H'\times [0,1]\to X$
,
![]() $\overline {I}(p,t):=I((I^1)^{-1}(p),1-t)$
. Given a second homotopy
$\overline {I}(p,t):=I((I^1)^{-1}(p),1-t)$
. Given a second homotopy
![]() $I'\colon H'\times [0,1]\to X$
between
$I'\colon H'\times [0,1]\to X$
between
![]() $H'$
and an embedded tree
$H'$
and an embedded tree
![]() $H''\subset X$
rel A, we obtain a homotopy between H and
$H''\subset X$
rel A, we obtain a homotopy between H and
![]() $H''$
rel A by forming the concatenation
$H''$
rel A by forming the concatenation
![]() $I\cdot I':H\times [0,1]\to X$
via
$I\cdot I':H\times [0,1]\to X$
via
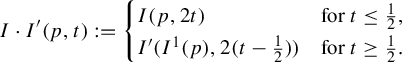 $$ \begin{align*} I\cdot I'(p,t):= \begin{cases} I(p,2t) & \text{for}~t\leq\tfrac{1}{2},\\ I'(I^1(p),2(t-\tfrac{1}{2})) & \text{for}~t\geq\tfrac{1}{2}. \end{cases} \end{align*} $$
$$ \begin{align*} I\cdot I'(p,t):= \begin{cases} I(p,2t) & \text{for}~t\leq\tfrac{1}{2},\\ I'(I^1(p),2(t-\tfrac{1}{2})) & \text{for}~t\geq\tfrac{1}{2}. \end{cases} \end{align*} $$
The concatenation satisfies
![]() $(I\cdot I')^1=(I')^1\circ I^1$
.
$(I\cdot I')^1=(I')^1\circ I^1$
.
Assume from now on that H is invariant up to homotopy rel
![]() $P(E_{\lambda })$
. While H is not forward invariant as a set, we still obtain a self-map of H which is well defined up to a certain equivalence relation: the homotopy
$P(E_{\lambda })$
. While H is not forward invariant as a set, we still obtain a self-map of H which is well defined up to a certain equivalence relation: the homotopy
![]() $I\colon H\times [0,1]\to \mathbb {C}_T$
from Definition 3.7 yields an identification of H and
$I\colon H\times [0,1]\to \mathbb {C}_T$
from Definition 3.7 yields an identification of H and
![]() $H'$
via the homeomorphism
$H'$
via the homeomorphism
![]() $\psi :=I_1\colon H\to H'$
and the composition
$\psi :=I_1\colon H\to H'$
and the composition
![]() $f:=\widehat {E_{\lambda }}\circ \psi \colon H\to H$
is a self-map of the tree H. We call f the induced self-map of H. There is a distinguished point
$f:=\widehat {E_{\lambda }}\circ \psi \colon H\to H$
is a self-map of the tree H. We call f the induced self-map of H. There is a distinguished point
![]() $v_T:=\psi ^{-1}(-\infty )\in H$
, the singular point of
$v_T:=\psi ^{-1}(-\infty )\in H$
, the singular point of
![]() $(H,f)$
, with the property that f is not injective at
$(H,f)$
, with the property that f is not injective at
![]() $v_T$
while it is a local homeomorphism elsewhere and its image
$v_T$
while it is a local homeomorphism elsewhere and its image
![]() $f(v_T)=0$
is the singular value. We call
$f(v_T)=0$
is the singular value. We call
![]() $V_f:=\{f^{\circ n}(v_T)~|~n\in \mathbb {N}_0\}\cup \{p\in H~|~\text {deg}_H(p)\geq 3\}$
the set of marked points of
$V_f:=\{f^{\circ n}(v_T)~|~n\in \mathbb {N}_0\}\cup \{p\in H~|~\text {deg}_H(p)\geq 3\}$
the set of marked points of
![]() $(H,f)$
. It is the union of the forward orbit of
$(H,f)$
. It is the union of the forward orbit of
![]() $v_T$
under f and the set of branch points of H, and, as such, contains
$v_T$
under f and the set of branch points of H, and, as such, contains
![]() $P(E_{\lambda })$
.
$P(E_{\lambda })$
.
Different homotopies between H and
![]() $H'$
yield different self-maps of H and we want to investigate this ambiguity. Let
$H'$
yield different self-maps of H and we want to investigate this ambiguity. Let
![]() $\varphi \colon H\to H'$
be another identification of H with
$\varphi \colon H\to H'$
be another identification of H with
![]() $H'$
obtained by a homotopy between H and
$H'$
obtained by a homotopy between H and
![]() $H'$
rel
$H'$
rel
![]() $P(E_{\lambda })$
, and let
$P(E_{\lambda })$
, and let
![]() $f':=\widehat {E_{\lambda }}\circ \varphi $
be the corresponding self-map of H and set
$f':=\widehat {E_{\lambda }}\circ \varphi $
be the corresponding self-map of H and set
![]() $v_T':=\varphi ^{-1}(-\infty )$
. As both maps
$v_T':=\varphi ^{-1}(-\infty )$
. As both maps
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
are induced by homotopies relative to
$\varphi $
are induced by homotopies relative to
![]() $P(E_{\lambda })$
, we have
$P(E_{\lambda })$
, we have
![]() $\psi (p)=\varphi (p)=p$
for all
$\psi (p)=\varphi (p)=p$
for all
![]() $p\in P(E_{\lambda })$
. Therefore the ‘change of identification’
$p\in P(E_{\lambda })$
. Therefore the ‘change of identification’
![]() $\theta :=\varphi ^{-1}\circ \psi \colon H\to H$
restricts to the identity on
$\theta :=\varphi ^{-1}\circ \psi \colon H\to H$
restricts to the identity on
![]() $P(E_{\lambda })$
and, in particular, on the set of endpoints of H. A (graph-theoretic) isomorphism between finite trees is uniquely determined by its values on endpoints; this implies
$P(E_{\lambda })$
and, in particular, on the set of endpoints of H. A (graph-theoretic) isomorphism between finite trees is uniquely determined by its values on endpoints; this implies
![]() $\theta (b)=b$
for all branch points
$\theta (b)=b$
for all branch points
![]() $b\in H$
. It might happen that
$b\in H$
. It might happen that
![]() $v_T\neq v_T'$
, but we still have
$v_T\neq v_T'$
, but we still have
![]() $\theta (v_T)=v_T'$
by definition of the singular point. We claim that
$\theta (v_T)=v_T'$
by definition of the singular point. We claim that
![]() $\theta (f(v))=f(v)$
for all
$\theta (f(v))=f(v)$
for all
![]() $v\in V_f$
. Indeed, if
$v\in V_f$
. Indeed, if
![]() $v\neq v_T$
is a branch point of H, then f is a local homeomorphism at v, so
$v\neq v_T$
is a branch point of H, then f is a local homeomorphism at v, so
![]() $f(v)$
is also a branch point of H, and we have
$f(v)$
is also a branch point of H, and we have
![]() $\theta (f(v))=f(v)$
. If
$\theta (f(v))=f(v)$
. If
![]() $v\in P(E_{\lambda })$
, then
$v\in P(E_{\lambda })$
, then
![]() $f(v)\in P(E_{\lambda })$
because
$f(v)\in P(E_{\lambda })$
because
![]() $P(E_{\lambda })$
is forward invariant under the dynamics of f, so again we have
$P(E_{\lambda })$
is forward invariant under the dynamics of f, so again we have
![]() $\theta (f(v))=f(v)$
. Finally, if
$\theta (f(v))=f(v)$
. Finally, if
![]() $v=v_T$
, then
$v=v_T$
, then
![]() $f(v_T)=0\in P(E_{\lambda })$
, so we have
$f(v_T)=0\in P(E_{\lambda })$
, so we have
![]() $\theta (f(v))=f(v)$
. It follows that
$\theta (f(v))=f(v)$
. It follows that
![]() $\theta $
restricts to a conjugation between f and
$\theta $
restricts to a conjugation between f and
![]() $f'$
on
$f'$
on
![]() $V_f$
because
$V_f$
because
![]() $\theta (f(v))=f(v)=f'(\theta (v))$
for all
$\theta (f(v))=f(v)=f'(\theta (v))$
for all
![]() $v\in V_f$
.
$v\in V_f$
.
It turns out that if we just replace the forward invariance condition of Hubbard trees by the weaker condition of being invariant up to homotopy rel
![]() $P(E_{\lambda })$
, the graph structure of the resulting tree is not uniquely determined. For example, if there exists a periodic branch point
$P(E_{\lambda })$
, the graph structure of the resulting tree is not uniquely determined. For example, if there exists a periodic branch point
![]() $b\in H$
of degree four, one can split it into two degree three branch points
$b\in H$
of degree four, one can split it into two degree three branch points
![]() $b_1$
and
$b_1$
and
![]() $b_2$
, changing the tree only in an arbitrary small neighborhood of b as indicated in Figure 1. If we perform this change consistently along the (forward and backward) orbit of b under the self-map f, we again obtain an invariant tree. Note, however, that in the new tree, we have
$b_2$
, changing the tree only in an arbitrary small neighborhood of b as indicated in Figure 1. If we perform this change consistently along the (forward and backward) orbit of b under the self-map f, we again obtain an invariant tree. Note, however, that in the new tree, we have
![]() $f^{\circ {n}}([b_1,b_2])=[b_1,b_2]$
, where n is the period of b (and hence also of
$f^{\circ {n}}([b_1,b_2])=[b_1,b_2]$
, where n is the period of b (and hence also of
![]() $b_1$
and
$b_1$
and
![]() $b_2$
) under f, that is, the in-tree connection of
$b_2$
) under f, that is, the in-tree connection of
![]() $b_1$
and
$b_1$
and
![]() $b_2$
is forward invariant.
$b_2$
is forward invariant.
Figure 1 Replacing one degree four branch point b by two degree three branch points
![]() $b_1$
and
$b_1$
and
![]() $b_2$
.
$b_2$
.
To obtain uniqueness of the graph structure, we want f to be expansive in the following sense.
Definition 3.8. (Expansive self-map)
The self-map
![]() $f\colon H\to H$
is called expansive if, for every pair of marked points
$f\colon H\to H$
is called expansive if, for every pair of marked points
![]() $p,q\in V_f$
with
$p,q\in V_f$
with
![]() $p\neq q$
, there exists an
$p\neq q$
, there exists an
![]() $n\geq 0$
such that
$n\geq 0$
such that
![]() $v_T\in f^{\circ n}([p,q])$
.
$v_T\in f^{\circ n}([p,q])$
.
Because different self-maps of H are conjugate on their sets of marked points, the definition of expansivity does not depend on the choice of homotopy between H and
![]() $H'$
. Again, the motivation for this definition comes from the polynomial case: the map obtained by restricting a unicritical polynomial with pre-periodic critical value to its Hubbard tree is always expansive in the sense that some iterated image of the in-tree connection of two marked points contains the unique critical point.
$H'$
. Again, the motivation for this definition comes from the polynomial case: the map obtained by restricting a unicritical polynomial with pre-periodic critical value to its Hubbard tree is always expansive in the sense that some iterated image of the in-tree connection of two marked points contains the unique critical point.
Summing up, we obtain the following definition of homotopy Hubbard trees for exponential maps.
Definition 3.9. (Homotopy Hubbard trees for exponential maps)
Let
![]() $E_{\lambda }$
be a post-singularly finite exponential map. A homotopy Hubbard tree
$E_{\lambda }$
be a post-singularly finite exponential map. A homotopy Hubbard tree
![]() $H\subset \mathbb {C}$
for
$H\subset \mathbb {C}$
for
![]() $E_{\lambda }$
is a finite embedded tree H such that the following conditions apply.
$E_{\lambda }$
is a finite embedded tree H such that the following conditions apply.
-
• H is spanned by
 $P(E_{\lambda })$
.
$P(E_{\lambda })$
. -
• H is invariant up to homotopy:
 $$ \begin{align*} H':=[P(E_{\lambda})]_{\widehat{E_{\lambda}}^{-1}(H)}\subset\mathbb{C}_T \text{ is homotopic to } H \text{ relative to } P(E_{\lambda}).\end{align*} $$
$$ \begin{align*} H':=[P(E_{\lambda})]_{\widehat{E_{\lambda}}^{-1}(H)}\subset\mathbb{C}_T \text{ is homotopic to } H \text{ relative to } P(E_{\lambda}).\end{align*} $$
-
• The induced self-map of H is expansive.
Homotopy Hubbard trees for exponential maps are only required to be invariant up to homotopy. To prove a meaningful uniqueness statement, we have to define a suitable equivalence relation on homotopy Hubbard trees that deals with the increased flexibility compared to the polynomial case. Naturally, being a homotopy Hubbard tree is a property of homotopy classes of embedded trees relative to the post-singular set.
Lemma 3.10. (Equivalent homotopy Hubbard trees)
Let
![]() $H,\tilde {H}\subset \mathbb {C}$
be finite embedded trees spanned by
$H,\tilde {H}\subset \mathbb {C}$
be finite embedded trees spanned by
![]() $P(E_{\lambda })$
and assume that H and
$P(E_{\lambda })$
and assume that H and
![]() $\tilde {H}$
are homotopic rel
$\tilde {H}$
are homotopic rel
![]() $P(E_{\lambda })$
. Then H is a homotopy Hubbard tree for
$P(E_{\lambda })$
. Then H is a homotopy Hubbard tree for
![]() $E_{\lambda }$
if and only if
$E_{\lambda }$
if and only if
![]() $\tilde {H}$
is a homotopy Hubbard tree for
$\tilde {H}$
is a homotopy Hubbard tree for
![]() $E_{\lambda }$
.
$E_{\lambda }$
.
Proof By symmetry of Definition 3.7, both directions are equivalent and it suffices to show one of them. Assume that H is a homotopy Hubbard tree for
![]() $E_{\lambda }$
, and let
$E_{\lambda }$
, and let
![]() $I_0$
be a homotopy between H and
$I_0$
be a homotopy between H and
![]() $\tilde {H}$
rel
$\tilde {H}$
rel
![]() $P(E_{\lambda })$
. In analogy to Lemma 3.5, one shows that
$P(E_{\lambda })$
. In analogy to Lemma 3.5, one shows that
![]() $I_0$
lifts to a homotopy
$I_0$
lifts to a homotopy
![]() $\widehat {I}_1\colon \widehat {E_{\lambda }}^{-1}(H)\times [0,1]\to \mathbb {C}_T$
between the pre-images of H and
$\widehat {I}_1\colon \widehat {E_{\lambda }}^{-1}(H)\times [0,1]\to \mathbb {C}_T$
between the pre-images of H and
![]() $\tilde {H}$
rel
$\tilde {H}$
rel
![]() $\widehat {E_{\lambda }}^{-1}(P(E_{\lambda }))$
. As
$\widehat {E_{\lambda }}^{-1}(P(E_{\lambda }))$
. As
![]() $P(E_{\lambda })\subset \widehat {E_{\lambda }}^{-1}(P(E_{\lambda }))$
, the homotopy
$P(E_{\lambda })\subset \widehat {E_{\lambda }}^{-1}(P(E_{\lambda }))$
, the homotopy
![]() $\widehat {I}_1$
fixes
$\widehat {I}_1$
fixes
![]() $P(E_{\lambda })$
pointwise, so the restriction
$P(E_{\lambda })$
pointwise, so the restriction
![]() $I_1:=\widehat {I}_1|_{H'\times [0,1]}$
is a homotopy between
$I_1:=\widehat {I}_1|_{H'\times [0,1]}$
is a homotopy between
![]() $H'$
and
$H'$
and
![]() $\tilde {H'}$
rel
$\tilde {H'}$
rel
![]() $P(E_{\lambda })$
. By the invariance of H, there exists a homotopy
$P(E_{\lambda })$
. By the invariance of H, there exists a homotopy
![]() $I\colon H\times [0,1]\to \mathbb {C}_T$
between H and
$I\colon H\times [0,1]\to \mathbb {C}_T$
between H and
![]() $H'$
. We see that
$H'$
. We see that
![]() $\tilde {H}$
is homotopic to
$\tilde {H}$
is homotopic to
![]() $\tilde {H}'$
rel
$\tilde {H}'$
rel
![]() $P(E_{\lambda })$
via the concatenation
$P(E_{\lambda })$
via the concatenation
![]() $\overline {I_0}\cdot I\cdot I_1$
. The self-map
$\overline {I_0}\cdot I\cdot I_1$
. The self-map
![]() $\tilde {f}:=\widehat {E_{\lambda }}\circ I_1^1\circ I^1 \circ \overline {I_0}^1$
of
$\tilde {f}:=\widehat {E_{\lambda }}\circ I_1^1\circ I^1 \circ \overline {I_0}^1$
of
![]() $\tilde {H}$
obtained via this homotopy is conjugate to the self-map
$\tilde {H}$
obtained via this homotopy is conjugate to the self-map
![]() $f:=\widehat {E_{\lambda }}\circ I^1$
of H. This can be seen using the fact that
$f:=\widehat {E_{\lambda }}\circ I^1$
of H. This can be seen using the fact that
![]() $\widehat {E_{\lambda }}\circ I_1^1=I_0^1\circ \widehat {E_{\lambda }}$
because
$\widehat {E_{\lambda }}\circ I_1^1=I_0^1\circ \widehat {E_{\lambda }}$
because
![]() $I_1^1$
is a lift of
$I_1^1$
is a lift of
![]() $I_0^1$
. Indeed,
$I_0^1$
. Indeed,
Therefore, the expansivity of
![]() $\tilde {f}$
follows from the expansivity of f.
$\tilde {f}$
follows from the expansivity of f.
Let us look more closely at the homotopy involved in the invariance condition of homotopy Hubbard trees. We want to see that after a small modification, this homotopy can be replaced by a stronger kind of homotopy called an ambient isotopy.
Definition 3.11. (Ambient isotopies)
Let X be a topological space and
![]() $A\subset X$
a subspace. Two embedded trees
$A\subset X$
a subspace. Two embedded trees
![]() $H,H'\subset X$
are called ambient isotopic relative to A if there exists a continuous map
$H,H'\subset X$
are called ambient isotopic relative to A if there exists a continuous map
![]() $I\colon X\times [0,1]\to X$
such that the following conditions are satisfied.
$I\colon X\times [0,1]\to X$
such that the following conditions are satisfied.
-
•
 $I(\cdot ,0)=\text {id}$
and
$I(\cdot ,0)=\text {id}$
and
 $I(H\times \{1\})=H'$
.
$I(H\times \{1\})=H'$
. -
• For each
 $a\in A$
, the homotopy I is constant on
$a\in A$
, the homotopy I is constant on
 $\{a\}\times [0,1]$
.
$\{a\}\times [0,1]$
. -
• For each
 $t\in [0,1]$
, the time-t map
$t\in [0,1]$
, the time-t map
 $I(\cdot ,t)\colon X\to X$
is a homeomorphism.
$I(\cdot ,t)\colon X\to X$
is a homeomorphism.
Two homeomorphisms
![]() $\varphi _0,\varphi _1\colon X\to X$
are called isotopic relative to A if there exists a homotopy between
$\varphi _0,\varphi _1\colon X\to X$
are called isotopic relative to A if there exists a homotopy between
![]() $\varphi _0$
and
$\varphi _0$
and
![]() $\varphi _1$
which is constant on A and restricts to a homeomorphism for each fixed
$\varphi _1$
which is constant on A and restricts to a homeomorphism for each fixed
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
The distinction between relative homotopy and isotopy is known to be subtle; in general,
![]() $\phi $
being homotopic to the identity
$\phi $
being homotopic to the identity
![]() $\text {id}$
rel A does not imply
$\text {id}$
rel A does not imply
![]() $\phi $
being isotopic to
$\phi $
being isotopic to
![]() $\text {id}$
rel A. In our setting, however, these notions are equivalent; we will use this in §6.
$\text {id}$
rel A. In our setting, however, these notions are equivalent; we will use this in §6.
Proposition 3.12. (E.g. [Reference Farb and MargalitFM, Theorem 1.12])
Let S be a closed oriented surface (that is, compact without boundary) and
![]() $A\subset S$
a finite set of marked points. An orientation-preserving homeomorphism
$A\subset S$
a finite set of marked points. An orientation-preserving homeomorphism
![]() $\phi \colon S\to S$
is homotopic to
$\phi \colon S\to S$
is homotopic to
![]() $\text {id}$
rel A if and only if it is isotopic to
$\text {id}$
rel A if and only if it is isotopic to
![]() $\text {id}$
rel A.
$\text {id}$
rel A.
For later use (in the proof of Proposition 4.9), we want to prove the following result regarding the homotopy involved in Definition 3.9.
Lemma 3.13. (On the invariance condition)
Let H be a homotopy Hubbard Tree for
![]() $E_{\lambda }$
. For every neighborhood
$E_{\lambda }$
. For every neighborhood
![]() $U\subset \mathbb {C}_T$
of
$U\subset \mathbb {C}_T$
of
![]() $-\infty $
, there exists an embedded tree
$-\infty $
, there exists an embedded tree
![]() $H''\subset \mathbb {C}$
such that
$H''\subset \mathbb {C}$
such that
![]() $H''$
is homotopic to
$H''$
is homotopic to
![]() $H'$
rel
$H'$
rel
![]() $\mathbb {C}_T\setminus U$
, and
$\mathbb {C}_T\setminus U$
, and
![]() $H''$
is ambient isotopic to H in
$H''$
is ambient isotopic to H in
![]() $\mathbb {C}$
rel
$\mathbb {C}$
rel
![]() $P(E_{\lambda })$
.
$P(E_{\lambda })$
.
One might hope to obtain an ambient isotopy between H and
![]() $H'$
rel
$H'$
rel
![]() $P(E_{\lambda })$
. Unfortunately, such an isotopy does not exist. The tree
$P(E_{\lambda })$
. Unfortunately, such an isotopy does not exist. The tree
![]() $H'$
contains
$H'$
contains
![]() $-\infty $
, while H does not, so the ambient isotopy would have to send
$-\infty $
, while H does not, so the ambient isotopy would have to send
![]() $-\infty $
to some point in the complex plane. However, the space
$-\infty $
to some point in the complex plane. However, the space
![]() $\mathbb {C}_T$
is not locally compact at
$\mathbb {C}_T$
is not locally compact at
![]() $-\infty $
, while it is locally compact at every point in the complex plane, so there does not exist a homeomorphism of
$-\infty $
, while it is locally compact at every point in the complex plane, so there does not exist a homeomorphism of
![]() $\mathbb {C}_T$
sending
$\mathbb {C}_T$
sending
![]() $-\infty $
to a point in the complex plane.
$-\infty $
to a point in the complex plane.
Therefore, we have to take an intermediate step, homotoping only the tree
![]() $H'$
to a tree
$H'$
to a tree
![]() $H''\subset \mathbb {C}$
. Then, we use a classical result on homotopies between graphs on surfaces to find an ambient isotopy between the modified tree
$H''\subset \mathbb {C}$
. Then, we use a classical result on homotopies between graphs on surfaces to find an ambient isotopy between the modified tree
![]() $H''$
and H.
$H''$
and H.
Lemma 3.14. (Homotoping
 $-\infty $
into the plane)
$-\infty $
into the plane)
Let
![]() $H\subset \mathbb {C}$
be a finite embedded tree spanned by
$H\subset \mathbb {C}$
be a finite embedded tree spanned by
![]() $P(E_{\lambda })$
and assume that
$P(E_{\lambda })$
and assume that
![]() $0$
is an endpoint of H. Let
$0$
is an endpoint of H. Let
![]() $H'=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}\subset \mathbb {C}_T$
be the subset of the pre-image tree spanned by
$H'=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}\subset \mathbb {C}_T$
be the subset of the pre-image tree spanned by
![]() $P(E_{\lambda })$
. For every neighborhood U of
$P(E_{\lambda })$
. For every neighborhood U of
![]() $-\infty $
in
$-\infty $
in
![]() $\mathbb {C}_T$
, there is a homotopy between
$\mathbb {C}_T$
, there is a homotopy between
![]() $H'$
and an embedded tree
$H'$
and an embedded tree
![]() $H''\subset \mathbb {C}$
relative to
$H''\subset \mathbb {C}$
relative to
![]() $\mathbb {C}_T\setminus U$
.
$\mathbb {C}_T\setminus U$
.
Proof The image
![]() $\tilde {V}:=\widehat {E_{\lambda }}(U)$
is a neighborhood of
$\tilde {V}:=\widehat {E_{\lambda }}(U)$
is a neighborhood of
![]() $0$
. As
$0$
. As
![]() $0$
is an endpoint of H, we can find a Jordan domain
$0$
is an endpoint of H, we can find a Jordan domain
![]() $V\subset \tilde {V}$
such that
$V\subset \tilde {V}$
such that
![]() $H\cap V=\operatorname {\mathrm {Tr}}(\gamma )$
for some arc
$H\cap V=\operatorname {\mathrm {Tr}}(\gamma )$
for some arc
![]() $\gamma \colon [0,1]\to \overline {V}$
connecting
$\gamma \colon [0,1]\to \overline {V}$
connecting
![]() $0$
to some point
$0$
to some point
![]() $v\in \partial V$
and satisfying
$v\in \partial V$
and satisfying
![]() $\gamma ([0,1))\subset V$
. The pre-image
$\gamma ([0,1))\subset V$
. The pre-image
![]() $\tilde {U}:=\widehat {E_{\lambda }}^{-1}(V)\subset U$
is a neighborhood of
$\tilde {U}:=\widehat {E_{\lambda }}^{-1}(V)\subset U$
is a neighborhood of
![]() $-\infty $
and
$-\infty $
and
![]() $\partial U\subset \mathbb {C}$
is a
$\partial U\subset \mathbb {C}$
is a
![]() $2\pi i$
-periodic arc. The pre-image curves of
$2\pi i$
-periodic arc. The pre-image curves of
![]() $\gamma $
have a natural vertical order and only finitely many of them are contained in
$\gamma $
have a natural vertical order and only finitely many of them are contained in
![]() $H'$
. Let
$H'$
. Let
![]() $\gamma _u$
be the uppermost and
$\gamma _u$
be the uppermost and
![]() $\gamma _l$
be the lowermost pre-image curves of
$\gamma _l$
be the lowermost pre-image curves of
![]() $\gamma $
contained in
$\gamma $
contained in
![]() $H'$
. The arcs
$H'$
. The arcs
![]() $\gamma _u$
and
$\gamma _u$
and
![]() $\gamma _l$
, together with the part of
$\gamma _l$
, together with the part of
![]() $\partial \tilde {U}$
between their endpoints on
$\partial \tilde {U}$
between their endpoints on
![]() $\partial \tilde {U}$
, bound a simply connected domain
$\partial \tilde {U}$
, bound a simply connected domain
![]() $D\subset \tilde {U}$
which is contained in
$D\subset \tilde {U}$
which is contained in
![]() $\mathbb {C}$
. The map
$\mathbb {C}$
. The map
![]() $\Phi \colon \mathbb {C}_T\to \overline {\mathbb {C}}$
, defined by
$\Phi \colon \mathbb {C}_T\to \overline {\mathbb {C}}$
, defined by
![]() $\Phi (z)=z$
for
$\Phi (z)=z$
for
![]() $z\in \mathbb {C}$
and
$z\in \mathbb {C}$
and
![]() $\Phi (-\infty )=\infty $
, is continuous and injective, but its inverse is not continuous. The domain
$\Phi (-\infty )=\infty $
, is continuous and injective, but its inverse is not continuous. The domain
![]() $\Phi (D)$
is a Jordan domain in
$\Phi (D)$
is a Jordan domain in
![]() $\overline {\mathbb {C}}$
and it is easy to see that
$\overline {\mathbb {C}}$
and it is easy to see that
![]() $\tilde {H}':=\Phi (H')$
is homotopic to a tree
$\tilde {H}':=\Phi (H')$
is homotopic to a tree
![]() $\tilde {H}''\subset \mathbb {C}$
rel
$\tilde {H}''\subset \mathbb {C}$
rel
![]() $\overline {\mathbb {C}}\setminus \operatorname {\mathrm {cl}}_{\overline {\mathbb {C}}}(D)$
. The closure
$\overline {\mathbb {C}}\setminus \operatorname {\mathrm {cl}}_{\overline {\mathbb {C}}}(D)$
. The closure
![]() $\text {cl}_{\mathbb {C}_T}(D)$
in the extended plane
$\text {cl}_{\mathbb {C}_T}(D)$
in the extended plane
![]() $\mathbb {C}_T$
is homeomorphic to its closure
$\mathbb {C}_T$
is homeomorphic to its closure
![]() $\text {cl}_{\overline {\mathbb {C}}}(D)$
on the Riemann sphere because every sequence
$\text {cl}_{\overline {\mathbb {C}}}(D)$
on the Riemann sphere because every sequence
![]() $(z_n)_n\subset D$
with
$(z_n)_n\subset D$
with
![]() $\lim _{n\to \infty }\lvert z_n \rvert =\infty $
satisfies
$\lim _{n\to \infty }\lvert z_n \rvert =\infty $
satisfies
![]() $\lim _{n\to \infty }\operatorname {Re}(z_n)=-\infty $
. (Note that this does not hold if we just require
$\lim _{n\to \infty }\operatorname {Re}(z_n)=-\infty $
. (Note that this does not hold if we just require
![]() $(z_n)_n\in U$
because the sequence could escape in the vertical direction.) Therefore, the homotopy between
$(z_n)_n\in U$
because the sequence could escape in the vertical direction.) Therefore, the homotopy between
![]() $\tilde {H}'$
and
$\tilde {H}'$
and
![]() $\tilde {H}''$
in
$\tilde {H}''$
in
![]() $\overline {\mathbb {C}}$
is pushed forward to a homotopy between
$\overline {\mathbb {C}}$
is pushed forward to a homotopy between
![]() $H'$
and some
$H'$
and some
![]() $H''\subset \mathbb {C}$
relative to
$H''\subset \mathbb {C}$
relative to
![]() $\mathbb {C}_T\setminus \text {cl}_{\mathbb {C}_T}(D)$
.
$\mathbb {C}_T\setminus \text {cl}_{\mathbb {C}_T}(D)$
.
It remains to show that
![]() $H''$
is ambient isotopic to H rel
$H''$
is ambient isotopic to H rel
![]() $P(E_{\lambda })$
in
$P(E_{\lambda })$
in
![]() $\mathbb {C}$
. The question under which conditions homotopic embedded graphs on a surface are ambient isotopic has already been studied extensively. One rather general result can be found in [Reference Farb and MargalitFM, Lemma 2.9]. We state a weaker version of this result that is sufficient for our purposes.
$\mathbb {C}$
. The question under which conditions homotopic embedded graphs on a surface are ambient isotopic has already been studied extensively. One rather general result can be found in [Reference Farb and MargalitFM, Lemma 2.9]. We state a weaker version of this result that is sufficient for our purposes.
Lemma 3.15. (Isotopies of curve systems on marked spheres)
Let
![]() $A\subset \overline {\mathbb {C}}$
be a finite set. Let
$A\subset \overline {\mathbb {C}}$
be a finite set. Let
![]() $\gamma _1$
, … ,
$\gamma _1$
, … ,
![]() $\gamma _n$
be a collection of pairwise non-homotopic proper arcs in
$\gamma _n$
be a collection of pairwise non-homotopic proper arcs in
![]() $\overline {\mathbb {C}}$
that do not intersect each other except possibly at their endpoints. If
$\overline {\mathbb {C}}$
that do not intersect each other except possibly at their endpoints. If
![]() $\gamma _1'$
, … ,
$\gamma _1'$
, … ,
![]() $\gamma _n'$
is another such collection so that
$\gamma _n'$
is another such collection so that
![]() $\gamma _i'$
is homotopic to
$\gamma _i'$
is homotopic to
![]() $\gamma _i$
relative to A for each i, then there exists an ambient isotopy
$\gamma _i$
relative to A for each i, then there exists an ambient isotopy
![]() $I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
rel A satisfying
$I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
rel A satisfying
![]() $I^1(\operatorname {\mathrm {Tr}}(\gamma _i))=\operatorname {\mathrm {Tr}}(\gamma _i')$
for all i simultaneously.
$I^1(\operatorname {\mathrm {Tr}}(\gamma _i))=\operatorname {\mathrm {Tr}}(\gamma _i')$
for all i simultaneously.
Here, a proper arc is an arc
![]() $\gamma \colon [0,1]\to \overline {\mathbb {C}}$
satisfying
$\gamma \colon [0,1]\to \overline {\mathbb {C}}$
satisfying
![]() $\gamma ^{-1}(A)=\{0,1\}$
, and two arcs are called homotopic rel A if they are homotopic rel A in the sense of Definition 3.7. We cannot apply Lemma 3.15 directly to our setting because no post-singular branch points of H are allowed to move during the homotopy, so there is no decomposition of H into proper arcs. The following lemma allows us to deal with this problem.
$\gamma ^{-1}(A)=\{0,1\}$
, and two arcs are called homotopic rel A if they are homotopic rel A in the sense of Definition 3.7. We cannot apply Lemma 3.15 directly to our setting because no post-singular branch points of H are allowed to move during the homotopy, so there is no decomposition of H into proper arcs. The following lemma allows us to deal with this problem.
Lemma 3.16. Let
![]() $D\subset \overline {\mathbb {C}}$
be a Jordan domain and let
$D\subset \overline {\mathbb {C}}$
be a Jordan domain and let
![]() $H,\tilde {H}\subset \overline {D}$
be finite embedded trees such that
$H,\tilde {H}\subset \overline {D}$
be finite embedded trees such that
![]() $H\cap \partial D=\tilde {H}\cap \partial D=\{p_1,\ldots , p_n\}$
, where the
$H\cap \partial D=\tilde {H}\cap \partial D=\{p_1,\ldots , p_n\}$
, where the
![]() $p_i$
are indexed according to their cyclic order on
$p_i$
are indexed according to their cyclic order on
![]() $\partial D$
. Assume that there exists a homeomorphism
$\partial D$
. Assume that there exists a homeomorphism
![]() $\varphi \colon H\to \tilde {H}$
, such that
$\varphi \colon H\to \tilde {H}$
, such that
![]() $\varphi (p_i)=p_i$
for all
$\varphi (p_i)=p_i$
for all
![]() $i\in \{1,\ldots , n\}$
, and that the set of endpoints of H (and therefore also of
$i\in \{1,\ldots , n\}$
, and that the set of endpoints of H (and therefore also of
![]() $\tilde {H}$
) is a subset of
$\tilde {H}$
) is a subset of
![]() $\{p_1,\ldots , p_n\}$
. Then H and
$\{p_1,\ldots , p_n\}$
. Then H and
![]() $\tilde {H}$
are ambient isotopic rel
$\tilde {H}$
are ambient isotopic rel
![]() $\partial D$
.
$\partial D$
.
Proof We prove a more general statement with H and
![]() $\tilde {H}$
replaced by finite unions of pairwise disjoint embedded trees. The points
$\tilde {H}$
replaced by finite unions of pairwise disjoint embedded trees. The points
![]() $p_i$
and the branch points of H are the vertices of H, and the subarcs of H joining adjacent vertices are the edges of H. The proof works through induction on the number of edges.
$p_i$
and the branch points of H are the vertices of H, and the subarcs of H joining adjacent vertices are the edges of H. The proof works through induction on the number of edges.
There exists a component T of H and an index i such that
![]() $p_i,p_{i+1}\in T$
. Let
$p_i,p_{i+1}\in T$
. Let
![]() $D'$
be the subdomain of D bounded by
$D'$
be the subdomain of D bounded by
![]() $[p_i,p_{i+1}]_H$
and
$[p_i,p_{i+1}]_H$
and
![]() $[p_{i+1},p_i]_{\partial D}$
. By hypothesis, we have
$[p_{i+1},p_i]_{\partial D}$
. By hypothesis, we have
![]() $H\subset \overline {D'}$
. Let
$H\subset \overline {D'}$
. Let
![]() $\tilde {T}$
be the component of
$\tilde {T}$
be the component of
![]() $\tilde {H}$
with the same endpoints. There exists an isotopy of
$\tilde {H}$
with the same endpoints. There exists an isotopy of
![]() $\overline {D}$
rel
$\overline {D}$
rel
![]() $\partial {D}$
mapping
$\partial {D}$
mapping
![]() $[p_i,p_{i+1}]_{\tilde {T}}$
to
$[p_i,p_{i+1}]_{\tilde {T}}$
to
![]() $[p_i,p_{i+1}]_T$
. Both
$[p_i,p_{i+1}]_T$
. Both
![]() $H'=\overline {H\cap D'}$
and
$H'=\overline {H\cap D'}$
and
![]() $\tilde {H}'=\overline {\tilde {H}\cap D'}$
consist of finitely many embedded trees with endpoints
$\tilde {H}'=\overline {\tilde {H}\cap D'}$
consist of finitely many embedded trees with endpoints
![]() $p_1',\ldots , p_m'\in \partial D$
, but the total number of edges of these trees has been reduced.
$p_1',\ldots , p_m'\in \partial D$
, but the total number of edges of these trees has been reduced.
Lemma 3.17. Let H be a homotopy Hubbard tree, and let
![]() $H''\subset \mathbb {C}$
be homotopic to
$H''\subset \mathbb {C}$
be homotopic to
![]() $H'=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
rel
$H'=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
rel
![]() $P(E_{\lambda })$
in
$P(E_{\lambda })$
in
![]() $\mathbb {C}_T$
. Then
$\mathbb {C}_T$
. Then
![]() $H''$
is ambient isotopic to H rel
$H''$
is ambient isotopic to H rel
![]() $P(E_{\lambda })$
in
$P(E_{\lambda })$
in
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Proof It is easy to see that
![]() $H''$
is homotopic to H rel
$H''$
is homotopic to H rel
![]() $P(E_{\lambda })$
in
$P(E_{\lambda })$
in
![]() $\mathbb {C}$
. Hence, it remains to show that
$\mathbb {C}$
. Hence, it remains to show that
![]() $H''$
is ambient isotopic to H relative to
$H''$
is ambient isotopic to H relative to
![]() $P(E_{\lambda })$
in
$P(E_{\lambda })$
in
![]() $\mathbb {C}$
. Choose a positively oriented simple closed curve
$\mathbb {C}$
. Choose a positively oriented simple closed curve
![]() $\Gamma \colon [0,1]\to \mathbb {C}$
with
$\Gamma \colon [0,1]\to \mathbb {C}$
with
![]() $\Gamma (0)=\Gamma (1)=0$
containing
$\Gamma (0)=\Gamma (1)=0$
containing
![]() $P(E_{\lambda })$
and satisfying the following properties.
$P(E_{\lambda })$
and satisfying the following properties.
-
• We can index the post-singular set as
 $P(E_{\lambda })=\{0=p_0,p_1,\ldots , p_n=p_0\}$
and subdivide
$P(E_{\lambda })=\{0=p_0,p_1,\ldots , p_n=p_0\}$
and subdivide
 $\Gamma $
into arcs
$\Gamma $
into arcs
 $\gamma _i\colon [t_i,t_{i+1}]\to \mathbb {C}$
(
$\gamma _i\colon [t_i,t_{i+1}]\to \mathbb {C}$
(
 $i\in \{0,\ldots , n-1\}$
) with
$i\in \{0,\ldots , n-1\}$
) with
 $\gamma _i(t_i)=p_i$
,
$\gamma _i(t_i)=p_i$
,
 $\gamma _i(t_{i+1})=p_{i+1}$
.
$\gamma _i(t_{i+1})=p_{i+1}$
. -
• We have
 $\gamma _i((t_i,t_{i+1}))\cap H=\emptyset $
for all
$\gamma _i((t_i,t_{i+1}))\cap H=\emptyset $
for all
 $i\in \{0,\ldots , n-1\}$
.
$i\in \{0,\ldots , n-1\}$
. -
•
 $\gamma _i$
is homotopic to the arc
$\gamma _i$
is homotopic to the arc
 $[p_i,p_{i+1}]_H$
relative to
$[p_i,p_{i+1}]_H$
relative to
 $P(E_{\lambda })$
.
$P(E_{\lambda })$
.
Hence,
![]() $\Gamma $
traverses the boundary of H touching it only once at every post-singular point. In the same way, we choose a simple closed curve
$\Gamma $
traverses the boundary of H touching it only once at every post-singular point. In the same way, we choose a simple closed curve
![]() $\Gamma ''$
that traverses the boundary of
$\Gamma ''$
that traverses the boundary of
![]() $H''$
. As H and
$H''$
. As H and
![]() $H''$
are homotopic relative to
$H''$
are homotopic relative to
![]() $P(E_{\lambda })$
,
$P(E_{\lambda })$
,
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\gamma _i''$
are homotopic rel
$\gamma _i''$
are homotopic rel
![]() $P(E_{\lambda })$
by the third property on the list. By Lemma 3.15, there is an ambient isotopy
$P(E_{\lambda })$
by the third property on the list. By Lemma 3.15, there is an ambient isotopy
![]() $I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
between
$I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
between
![]() $\cup \gamma _i$
and
$\cup \gamma _i$
and
![]() $\cup \gamma _i''$
relative to
$\cup \gamma _i''$
relative to
![]() $P(E_{\lambda })\cup \{\infty \}$
. The curve
$P(E_{\lambda })\cup \{\infty \}$
. The curve
![]() $\Gamma ''$
traverses the boundaries of
$\Gamma ''$
traverses the boundaries of
![]() $H^1:=I^1(H)$
and
$H^1:=I^1(H)$
and
![]() $H''$
simultaneously. By Lemma 3.16, the trees
$H''$
simultaneously. By Lemma 3.16, the trees
![]() $H^1$
and
$H^1$
and
![]() $H''$
are ambient isotopic rel
$H''$
are ambient isotopic rel
![]() $\operatorname {\mathrm {Tr}}(\Gamma '')\supset P(E_{\lambda })$
.
$\operatorname {\mathrm {Tr}}(\Gamma '')\supset P(E_{\lambda })$
.
4 The triod algorithm: determining the graph structure
In this section, we show that for a fixed post-singularly finite exponential map, the structure of a homotopy Hubbard tree as a dynamical tree (see Definition 4.2) is uniquely determined by the kneading sequence (see Definition 2.11) of the external address of a ray landing at the singular value. Together with the fact that a homotopy Hubbard tree does not intersect dynamic rays landing at post-singular points (up to homotopy), this implies uniqueness of homotopy Hubbard trees.
If several dynamic rays land at the singular value, the kneading sequences of their external addresses agree by the following lemma, so we speak of the kneading sequence of a post-singularly finite exponential map. A proof of the result can be found in [Reference Laubner, Schleicher and VicolLSV, Proof of Theorem 2.7,
![]() $(1)\Rightarrow (5)$
].
$(1)\Rightarrow (5)$
].
Lemma 4.1. (Different dynamical partitions)
Let
![]() $E_{\lambda }$
be a psf exponential map for which the dynamic rays
$E_{\lambda }$
be a psf exponential map for which the dynamic rays
![]() $g_{\underline {s}}$
and
$g_{\underline {s}}$
and
![]() $g_{\underline {s'}}$
both land at
$g_{\underline {s'}}$
both land at
![]() $0$
. Then the kneading sequences
$0$
. Then the kneading sequences
![]() $\operatorname {\mathrm {It}}(\underline {s}'~\vert ~\underline {s'})$
and
$\operatorname {\mathrm {It}}(\underline {s}'~\vert ~\underline {s'})$
and
![]() $\operatorname {\mathrm {It}}(\underline {s}~\vert ~\underline {s})$
agree. Therefore, a post-singular point
$\operatorname {\mathrm {It}}(\underline {s}~\vert ~\underline {s})$
agree. Therefore, a post-singular point
![]() $p\in P(E_{\lambda })$
is contained in the ith sector
$p\in P(E_{\lambda })$
is contained in the ith sector
![]() $D_i$
of
$D_i$
of
![]() $\mathcal {D}$
if and only if it is contained in the ith sector
$\mathcal {D}$
if and only if it is contained in the ith sector
![]() $D_i'$
of
$D_i'$
of
![]() $\mathcal {D}'$
.
$\mathcal {D}'$
.
Let H be a homotopy Hubbard tree and f be an induced self-map of H. We will see that two post-singular points are contained in the same branch of H at the singular point
![]() $v_T$
if and only if their itineraries start with the same integer
$v_T$
if and only if their itineraries start with the same integer
![]() $k_i$
, and we index the different branches
$k_i$
, and we index the different branches
![]() $B_{k_i}$
by the corresponding integers. If we accept this fact for the moment, the triple
$B_{k_i}$
by the corresponding integers. If we accept this fact for the moment, the triple
![]() $(H,f,B_{k_i})$
satisfies the following definition.
$(H,f,B_{k_i})$
satisfies the following definition.
Definition 4.2. (Exponential dynamical tree)
An exponential dynamical tree is a triple
![]() $(H,f,B_{k_i})$
, where H is a finite topological tree and
$(H,f,B_{k_i})$
, where H is a finite topological tree and
![]() $f\colon H\to H$
is a self-map of H satisfying the following conditions.
$f\colon H\to H$
is a self-map of H satisfying the following conditions.
-
• There exists a distinguished point
 $v_T\in H$
, the singular point, such that f is not injective at
$v_T\in H$
, the singular point, such that f is not injective at
 $v_T$
, whereas f is a local homeomorphism at each point
$v_T$
, whereas f is a local homeomorphism at each point
 $p\in H\setminus \{v_T\}$
.
$p\in H\setminus \{v_T\}$
. -
• All endpoints of H are on the singular orbit.
-
• The singular value
 $f(v_T)$
is strictly pre-periodic.
$f(v_T)$
is strictly pre-periodic. -
• If
 $p,q\in H$
with
$p,q\in H$
with
 $p\neq q$
are branch points or points on the singular orbit, then there is an
$p\neq q$
are branch points or points on the singular orbit, then there is an
 $n\geq 0$
such that
$n\geq 0$
such that
 $f^{\circ n}([p,q])$
contains the singular point
$f^{\circ n}([p,q])$
contains the singular point
 $v_T$
(expansivity).
$v_T$
(expansivity).
In addition, the connected components
![]() $B_{k_0}, B_{k_1},\ldots , B_{k_n}$
of
$B_{k_0}, B_{k_1},\ldots , B_{k_n}$
of
![]() $H\setminus \{v_T\}$
are indexed by distinct integers
$H\setminus \{v_T\}$
are indexed by distinct integers
![]() $k_i\in \mathbb {Z}$
such that
$k_i\in \mathbb {Z}$
such that
![]() $k_0=0$
and
$k_0=0$
and
![]() $f(v_T)\in B_0$
.
$f(v_T)\in B_0$
.
The set
![]() $V_f$
of marked points consists of the forward orbit of
$V_f$
of marked points consists of the forward orbit of
![]() $v_T$
under f (including
$v_T$
under f (including
![]() $v_T$
) and the set of branch points of H.
$v_T$
) and the set of branch points of H.
We call two exponential dynamical trees
![]() $(H,f,B_{k_i})$
and
$(H,f,B_{k_i})$
and
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
equivalent if there exists a homeomorphism
$(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
equivalent if there exists a homeomorphism
![]() $\varphi \colon H\to \tilde {H}$
that restricts to a conjugation between f and
$\varphi \colon H\to \tilde {H}$
that restricts to a conjugation between f and
![]() $\tilde {f}$
on the set of marked points
$\tilde {f}$
on the set of marked points
![]() $V_f$
and maps each branch
$V_f$
and maps each branch
![]() $B_{k_i}$
to the branch
$B_{k_i}$
to the branch
![]() $\tilde {B}_{k_i}$
of the same index.
$\tilde {B}_{k_i}$
of the same index.
Let us state some simple properties of exponential dynamical trees first. Their proof is not very hard and works in complete analogy to the proof of [Reference Bruin, Kaffl and SchleicherBKS, Lemma 2.3], so we omit it here.
Lemma 4.3. (Basic properties of exponential dynamical trees)
Let
![]() $(H,f,B_{k_i})$
be an exponential dynamical tree. The singular value
$(H,f,B_{k_i})$
be an exponential dynamical tree. The singular value
![]() $f(v_T)$
is an endpoint of H. Each branch point is periodic or pre-periodic. The restriction of f to any branch of H at
$f(v_T)$
is an endpoint of H. Each branch point is periodic or pre-periodic. The restriction of f to any branch of H at
![]() $v_T$
is injective.
$v_T$
is injective.
We have seen in the previous section that different self-maps of a homotopy Hubbard tree H yield equivalent exponential dynamical trees (see the paragraphs after Definition 3.7). Furthermore, if
![]() $\tilde {H}$
and H are equivalent homotopy Hubbard trees, we can choose their induced self-maps to be conjugate to each other (see the proof of Lemma 3.10). Therefore, we obtain a well-defined map from the set of equivalence classes of homotopy Hubbard trees to the set of equivalence classes of exponential dynamical trees. The main goal of this section is to give a constructive proof of the following statement.
$\tilde {H}$
and H are equivalent homotopy Hubbard trees, we can choose their induced self-maps to be conjugate to each other (see the proof of Lemma 3.10). Therefore, we obtain a well-defined map from the set of equivalence classes of homotopy Hubbard trees to the set of equivalence classes of exponential dynamical trees. The main goal of this section is to give a constructive proof of the following statement.
Theorem 4.4. Let H and
![]() $\tilde {H}$
be two homotopy Hubbard trees for a post-singularly finite exponential map
$\tilde {H}$
be two homotopy Hubbard trees for a post-singularly finite exponential map
![]() $E_{\lambda }$
. Then H and
$E_{\lambda }$
. Then H and
![]() $\tilde {H}$
yield equivalent exponential dynamical trees.
$\tilde {H}$
yield equivalent exponential dynamical trees.
Note that we do not require H and
![]() $\tilde {H}$
to be equivalent. The proof of this theorem works in two steps. To explain the outline of the proof, we also have to define kneading sequences for exponential dynamical trees.
$\tilde {H}$
to be equivalent. The proof of this theorem works in two steps. To explain the outline of the proof, we also have to define kneading sequences for exponential dynamical trees.
Definition 4.5. (Itineraries and kneading sequence)
Let
![]() $(H,f,B_{k_i})$
be an exponential dynamical tree. The itinerary of a point
$(H,f,B_{k_i})$
be an exponential dynamical tree. The itinerary of a point
![]() $p\in H$
is the infinite sequence
$p\in H$
is the infinite sequence
![]() $\operatorname {\mathrm {It}}(p)=\mathtt {\underline {t}}=\mathtt {t_1 t_2\ldots }$
where
$\operatorname {\mathrm {It}}(p)=\mathtt {\underline {t}}=\mathtt {t_1 t_2\ldots }$
where
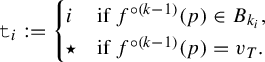 $$ \begin{align*} \mathtt{t}_i:= \begin{cases} i & \text{if } f^{\circ (k-1)}(p)\in B_{k_i},\\ \star & \text{if } f^{\circ (k-1)}(p)=v_T. \end{cases} \end{align*} $$
$$ \begin{align*} \mathtt{t}_i:= \begin{cases} i & \text{if } f^{\circ (k-1)}(p)\in B_{k_i},\\ \star & \text{if } f^{\circ (k-1)}(p)=v_T. \end{cases} \end{align*} $$
The itinerary
![]() $\operatorname {\mathrm {It}}(f(v_T))=:\nu =\nu _1\nu _2\ldots $
of the singular value is called the kneading sequence of
$\operatorname {\mathrm {It}}(f(v_T))=:\nu =\nu _1\nu _2\ldots $
of the singular value is called the kneading sequence of
![]() $(H,f,B_{k_i})$
.
$(H,f,B_{k_i})$
.
The proof of Theorem 4.4 works in two steps. First we show that different homotopy Hubbard trees for the same psf exponential map yield exponential dynamical trees with equal kneading sequences. The second step is to show that an exponential dynamical tree is already determined (up to equivalence) by its kneading sequence.
To prove the first statement, we will show that for every homotopy Hubbard tree, there exists a dynamic ray landing at
![]() $0$
such that, up to homotopy, the tree does not intersect the ray. Therefore, the pre-image of the tree does not intersect the boundary of the corresponding dynamical partition (up to homotopy). This implies the statement above because itineraries are independent of the choice of partition by Lemma 4.1 and every partition sector contains at most one branch of
$0$
such that, up to homotopy, the tree does not intersect the ray. Therefore, the pre-image of the tree does not intersect the boundary of the corresponding dynamical partition (up to homotopy). This implies the statement above because itineraries are independent of the choice of partition by Lemma 4.1 and every partition sector contains at most one branch of
![]() $H'=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
at
$H'=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
at
![]() $-\infty $
.
$-\infty $
.
For the proof, we need a topological characterization of dynamic rays landing at periodic post-singular points. Let
![]() $p\in P(E_{\lambda })$
be periodic. An arc
$p\in P(E_{\lambda })$
be periodic. An arc
![]() $\gamma \colon [0,1]\to \overline {\mathbb {C}}$
with
$\gamma \colon [0,1]\to \overline {\mathbb {C}}$
with
![]() $\gamma (0)=p$
,
$\gamma (0)=p$
,
![]() $\gamma (1)=\infty $
, and
$\gamma (1)=\infty $
, and
![]() $\operatorname {\mathrm {Tr}}(\gamma )\cap P(E_{\lambda })=\{p\}$
is called a leg at p. We denote its homotopy class relative to
$\operatorname {\mathrm {Tr}}(\gamma )\cap P(E_{\lambda })=\{p\}$
is called a leg at p. We denote its homotopy class relative to
![]() $P(E_{\lambda })\cup \{\infty \}$
by
$P(E_{\lambda })\cup \{\infty \}$
by
![]() $[\gamma ]$
. By definition, a leg
$[\gamma ]$
. By definition, a leg
![]() $\tilde {\gamma }$
at p is in the same homotopy class as
$\tilde {\gamma }$
at p is in the same homotopy class as
![]() $\gamma $
if there is a homotopy between
$\gamma $
if there is a homotopy between
![]() $\gamma $
and
$\gamma $
and
![]() $\tilde {\gamma }$
in
$\tilde {\gamma }$
in
![]() $\overline {\mathbb {C}}\setminus (P(E_{\lambda })\setminus \{p\})$
fixing the endpoints.
$\overline {\mathbb {C}}\setminus (P(E_{\lambda })\setminus \{p\})$
fixing the endpoints.
For every leg
![]() $\gamma $
, we set
$\gamma $
, we set
![]() $\tilde {\mathcal {L}}(\gamma )=\Gamma $
, where
$\tilde {\mathcal {L}}(\gamma )=\Gamma $
, where
![]() $\Gamma \colon [0,1]\to \overline {\mathbb {C}}$
with
$\Gamma \colon [0,1]\to \overline {\mathbb {C}}$
with
![]() $\Gamma (0)=p'$
and
$\Gamma (0)=p'$
and
![]() $\Gamma (1)=\infty $
is the lift of
$\Gamma (1)=\infty $
is the lift of
![]() $\gamma $
starting at the unique periodic pre-image
$\gamma $
starting at the unique periodic pre-image
![]() $p'$
of p. Lifting is always possible as
$p'$
of p. Lifting is always possible as
![]() $0\notin \operatorname {\mathrm {Tr}}(\gamma )$
and
$0\notin \operatorname {\mathrm {Tr}}(\gamma )$
and
![]() $E_{\lambda }\colon \mathbb {C}\to \mathbb {C}\setminus \{0\}$
is a covering map. As
$E_{\lambda }\colon \mathbb {C}\to \mathbb {C}\setminus \{0\}$
is a covering map. As
![]() $P(E_{\lambda })$
is forward invariant, the arc
$P(E_{\lambda })$
is forward invariant, the arc
![]() $\Gamma $
satisfies
$\Gamma $
satisfies
![]() $\operatorname {\mathrm {Tr}}(\Gamma )\cap P(E_{\lambda })=\{p'\}$
, so
$\operatorname {\mathrm {Tr}}(\Gamma )\cap P(E_{\lambda })=\{p'\}$
, so
![]() $\Gamma $
is a leg at
$\Gamma $
is a leg at
![]() $p'$
.
$p'$
.
The map
![]() $\tilde {\mathcal {L}}$
defined in this way descends to a well-defined map
$\tilde {\mathcal {L}}$
defined in this way descends to a well-defined map
![]() $\mathcal {L}([\gamma ])=[\Gamma ]$
because homotopies lift under covering maps. We call
$\mathcal {L}([\gamma ])=[\Gamma ]$
because homotopies lift under covering maps. We call
![]() $\mathcal {L}$
the leg map, using the terminology from [Reference Mihaljević-BrandtB, Definition 4.3].
$\mathcal {L}$
the leg map, using the terminology from [Reference Mihaljević-BrandtB, Definition 4.3].
Proposition 4.6. (Topological characterization of dynamic rays)
Let
![]() $p\in P(E_{\lambda })$
be periodic and let
$p\in P(E_{\lambda })$
be periodic and let
![]() $\gamma $
be a leg at p. There exists a dynamic ray
$\gamma $
be a leg at p. There exists a dynamic ray
![]() $g\in [\gamma ]$
if and only if
$g\in [\gamma ]$
if and only if
![]() $[\gamma ]$
is periodic under the leg map.
$[\gamma ]$
is periodic under the leg map.
If
![]() $[\gamma ]$
is periodic under the leg map, the ray
$[\gamma ]$
is periodic under the leg map, the ray
![]() $g\in [\gamma ]$
is unique. Stated differently, distinct dynamic rays are not homotopic rel
$g\in [\gamma ]$
is unique. Stated differently, distinct dynamic rays are not homotopic rel
![]() $P(E_{\lambda })\cup \infty $
.
$P(E_{\lambda })\cup \infty $
.
Proof It is clear that
![]() $[\gamma ]$
is periodic under iteration of
$[\gamma ]$
is periodic under iteration of
![]() $\mathcal {L}$
if there is a dynamic ray
$\mathcal {L}$
if there is a dynamic ray
![]() $g\in [\gamma ]$
: every dynamic ray landing at a periodic point is periodic as a set, so
$g\in [\gamma ]$
: every dynamic ray landing at a periodic point is periodic as a set, so
![]() $[g]=[\gamma ]$
is periodic under the leg map. The proof of the other direction is essentially the same as the proof of [Reference Mihaljević-BrandtB, Theorem 4.11]. Every iterate
$[g]=[\gamma ]$
is periodic under the leg map. The proof of the other direction is essentially the same as the proof of [Reference Mihaljević-BrandtB, Theorem 4.11]. Every iterate
![]() $f:=E_{\lambda }^{\circ n}$
has the same dynamic rays as
$f:=E_{\lambda }^{\circ n}$
has the same dynamic rays as
![]() $E_{\lambda }$
, so by passing to a suitable iterate f, we can assume that
$E_{\lambda }$
, so by passing to a suitable iterate f, we can assume that
![]() $[\gamma ]$
is fixed under iteration of the leg map for f. Applying the leg map to
$[\gamma ]$
is fixed under iteration of the leg map for f. Applying the leg map to
![]() $[\gamma ]$
at least twice, we can further assume that
$[\gamma ]$
at least twice, we can further assume that
![]() $\gamma $
is eventually contained in a single fundamental domain
$\gamma $
is eventually contained in a single fundamental domain
![]() $F_0$
for f for some static partition of f. One can then prove just as in [Reference Mihaljević-BrandtB, Theorem 4.11] that
$F_0$
for f for some static partition of f. One can then prove just as in [Reference Mihaljević-BrandtB, Theorem 4.11] that
![]() $\gamma $
is homotopic to the dynamic ray
$\gamma $
is homotopic to the dynamic ray
![]() $g_{\underline {t}}$
of f with external address
$g_{\underline {t}}$
of f with external address
![]() $\underline {t}=F_0 F_0\ldots\, $
. If there was a second dynamic ray
$\underline {t}=F_0 F_0\ldots\, $
. If there was a second dynamic ray
![]() $g'\in [\gamma ]$
, it would also have external address
$g'\in [\gamma ]$
, it would also have external address
![]() $\underline {t}$
, which would contradict the fact that every external address is the address of at most one ray. See [Reference Mihaljević-BrandtB] for the definition of the terminology and the details of the proof.
$\underline {t}$
, which would contradict the fact that every external address is the address of at most one ray. See [Reference Mihaljević-BrandtB] for the definition of the terminology and the details of the proof.
Remark 4.7. We are slightly imprecise in the formulation of Proposition 4.6: a dynamic ray
![]() $g\colon (0,\infty )\to \overline {\mathbb {C}}$
landing at p neither contains p nor
$g\colon (0,\infty )\to \overline {\mathbb {C}}$
landing at p neither contains p nor
![]() $\infty $
by Definition 2.2. When talking about the homotopy class of g, we treat it as an arc in
$\infty $
by Definition 2.2. When talking about the homotopy class of g, we treat it as an arc in
![]() $\overline {\mathbb {C}}$
containing its endpoints p and
$\overline {\mathbb {C}}$
containing its endpoints p and
![]() $\infty $
, so that g becomes a leg at p.
$\infty $
, so that g becomes a leg at p.
We prove that for every access to a homotopy Hubbard tree at a post-singular point, there exists a dynamic ray that approaches H through this access and does not intersect H up to homotopy. Before stating the theorem, let us formally define what we mean by an access.
Definition 4.8. (Accesses)
Let H be a homotopy Hubbard tree for
![]() $E_{\lambda }$
. An access to H at
$E_{\lambda }$
. An access to H at
![]() $p\in P(E_{\lambda })$
is a prime end
$p\in P(E_{\lambda })$
is a prime end
![]() $A=[\{N_j\}]$
for the pair
$A=[\{N_j\}]$
for the pair
![]() $(\overline {\mathbb {C}}\setminus H, H)$
with impression
$(\overline {\mathbb {C}}\setminus H, H)$
with impression
![]() $\{p\}$
(see [Reference MilnorM, §17]).
$\{p\}$
(see [Reference MilnorM, §17]).
We say that a leg
![]() $\gamma \colon [0,1]\to \overline {\mathbb {C}}$
approaches p through A if
$\gamma \colon [0,1]\to \overline {\mathbb {C}}$
approaches p through A if
![]() $\gamma (0)=p$
,
$\gamma (0)=p$
,
![]() $\gamma ((0,1])\cap H=\emptyset $
, and, for every
$\gamma ((0,1])\cap H=\emptyset $
, and, for every
![]() $j\in \mathbb {N}$
, we have
$j\in \mathbb {N}$
, we have
![]() $\gamma (t)\in N_j$
for
$\gamma (t)\in N_j$
for
![]() $t>0$
small enough.
$t>0$
small enough.
Proposition 4.9. (Accesses contain dynamic rays)
Let H be a homotopy Hubbard tree for
![]() $E_{\lambda }$
. There exists an equivalent homotopy Hubbard tree
$E_{\lambda }$
. There exists an equivalent homotopy Hubbard tree
![]() $\tilde {H}\cong H$
such that for each post-singular point
$\tilde {H}\cong H$
such that for each post-singular point
![]() $p\in P(E_{\lambda })$
and each access A to p in
$p\in P(E_{\lambda })$
and each access A to p in
![]() $\tilde {H}$
, there exists a dynamic ray g approaching p through A.
$\tilde {H}$
, there exists a dynamic ray g approaching p through A.
Proof Let
![]() $\{0=p_0,p_1=E_{\lambda }(p_0),\ldots ,p_n=E_{\lambda }^{\circ n}(p_0), p_{n+1}=p_{l+1}\}$
be the post-singular orbit, where
$\{0=p_0,p_1=E_{\lambda }(p_0),\ldots ,p_n=E_{\lambda }^{\circ n}(p_0), p_{n+1}=p_{l+1}\}$
be the post-singular orbit, where
![]() $p_{l+1}$
is the first periodic point on the forward orbit of
$p_{l+1}$
is the first periodic point on the forward orbit of
![]() $0$
. Denote the accesses to H at
$0$
. Denote the accesses to H at
![]() $p_m$
by
$p_m$
by
![]() $A_m^{(1)},\ldots , A_m^{(d_m)}$
, where
$A_m^{(1)},\ldots , A_m^{(d_m)}$
, where
![]() $d_m\in \mathbb {N}$
is the number of branches of H at
$d_m\in \mathbb {N}$
is the number of branches of H at
![]() $p_m$
and the accesses
$p_m$
and the accesses
![]() $A_m^{(i)}$
are numbered according to their cyclic order at
$A_m^{(i)}$
are numbered according to their cyclic order at
![]() $p_m$
. For every access
$p_m$
. For every access
![]() $A_m^{(i)}$
, choose a leg
$A_m^{(i)}$
, choose a leg
![]() $\gamma _m^{(i)}\colon [0,1]\to \overline {\mathbb {C}}$
approaching
$\gamma _m^{(i)}\colon [0,1]\to \overline {\mathbb {C}}$
approaching
![]() $p_m$
through
$p_m$
through
![]() $A_m^{(i)}$
. Note that if
$A_m^{(i)}$
. Note that if
![]() $\Gamma _m^{(i)}$
is another leg approaching
$\Gamma _m^{(i)}$
is another leg approaching
![]() $p_m$
through
$p_m$
through
![]() $A_m^{(i)}$
, then
$A_m^{(i)}$
, then
![]() $\gamma _m^{(i)}$
is homotopic to
$\gamma _m^{(i)}$
is homotopic to
![]() $\Gamma _m^{(i)}$
rel
$\Gamma _m^{(i)}$
rel
![]() $P(E_{\lambda })$
(which is easy to see using the theory of prime ends). We first consider the periodic part of the forward orbit of
$P(E_{\lambda })$
(which is easy to see using the theory of prime ends). We first consider the periodic part of the forward orbit of
![]() $0$
. For
$0$
. For
![]() $m\in \{l+1,\ldots ,n\}$
, the number of branches of H at
$m\in \{l+1,\ldots ,n\}$
, the number of branches of H at
![]() $p_m$
is independent of m (say equal to
$p_m$
is independent of m (say equal to
![]() $d\in \mathbb {N}$
) because the induced self-map
$d\in \mathbb {N}$
) because the induced self-map
![]() $f\colon H\to H$
is a local homeomorphism at
$f\colon H\to H$
is a local homeomorphism at
![]() $p_m$
and
$p_m$
and
![]() $p_m$
is periodic. Choose a neighborhood V of
$p_m$
is periodic. Choose a neighborhood V of
![]() $0$
such that none of the legs
$0$
such that none of the legs
![]() $\gamma _m^{(i)}$
for
$\gamma _m^{(i)}$
for
![]() $m\in \{l+1,\ldots , n\}$
intersect V. We set
$m\in \{l+1,\ldots , n\}$
intersect V. We set
![]() $U:=\widehat {E_{\lambda }}^{-1}(V)$
and apply Lemma 3.13 to obtain an embedded tree
$U:=\widehat {E_{\lambda }}^{-1}(V)$
and apply Lemma 3.13 to obtain an embedded tree
![]() $H''\subset \mathbb {C}$
homotopic to
$H''\subset \mathbb {C}$
homotopic to
![]() $H'$
rel
$H'$
rel
![]() $\mathbb {C}_T\setminus U$
. The lifts
$\mathbb {C}_T\setminus U$
. The lifts
![]() $\tilde {\mathcal {L}}(\gamma _m^{(i)})$
of the
$\tilde {\mathcal {L}}(\gamma _m^{(i)})$
of the
![]() $\gamma _m^{(i)}$
along the periodic post-singular orbit do not intersect U and therefore are disjoint from
$\gamma _m^{(i)}$
along the periodic post-singular orbit do not intersect U and therefore are disjoint from
![]() $H''$
(as
$H''$
(as
![]() $H'$
and
$H'$
and
![]() $H''$
are equal on
$H''$
are equal on
![]() $\mathbb {C}\setminus U$
) except for their endpoints. Now we see why we need Lemma 3.13: there exists an ambient isotopy
$\mathbb {C}\setminus U$
) except for their endpoints. Now we see why we need Lemma 3.13: there exists an ambient isotopy
![]() $I\colon \mathbb {C}\times [0,1]\to \mathbb {C}$
between
$I\colon \mathbb {C}\times [0,1]\to \mathbb {C}$
between
![]() $H''$
and H rel
$H''$
and H rel
![]() $P(E_{\lambda })$
, and it extends to an ambient isotopy
$P(E_{\lambda })$
, and it extends to an ambient isotopy
![]() $I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
fixing
$I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
fixing
![]() $\infty $
. Hence,
$\infty $
. Hence,
![]() $\Gamma _m^{(i)}:= I|_{\overline {\mathbb {C}}\times \{1\}}(\tilde {\mathcal {L}}(\gamma _m^{(i)}))$
approaches
$\Gamma _m^{(i)}:= I|_{\overline {\mathbb {C}}\times \{1\}}(\tilde {\mathcal {L}}(\gamma _m^{(i)}))$
approaches
![]() $p_{m-1}$
(or
$p_{m-1}$
(or
![]() $p_n$
for
$p_n$
for
![]() $m=l+1$
) through an access
$m=l+1$
) through an access
![]() $A_{m-1}^{(\sigma _m(i))}$
. By the above,
$A_{m-1}^{(\sigma _m(i))}$
. By the above,
![]() $\Gamma _m^{(i)}$
is homotopic to
$\Gamma _m^{(i)}$
is homotopic to
![]() $\gamma _{m-1}^{(\sigma _m(i))}$
, so we have
$\gamma _{m-1}^{(\sigma _m(i))}$
, so we have
As
![]() $E_{\lambda }$
is locally an orientation-preserving homeomorphism and as ambient isotopies preserve the cyclic order of curves landing at a common point, we see that each
$E_{\lambda }$
is locally an orientation-preserving homeomorphism and as ambient isotopies preserve the cyclic order of curves landing at a common point, we see that each
![]() $\sigma _m\colon \{1,\ldots ,d\}\to \{1,\ldots ,d\}$
is a power of the d-cycle
$\sigma _m\colon \{1,\ldots ,d\}\to \{1,\ldots ,d\}$
is a power of the d-cycle
![]() $(1~2~\ldots ~d)$
. Therefore, there exists an
$(1~2~\ldots ~d)$
. Therefore, there exists an
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $\mathcal {L}^{\circ N}([\gamma _m^{(i)}])=[\gamma _m^{(i)}]$
for all m and i. By Proposition 4.6, each
$\mathcal {L}^{\circ N}([\gamma _m^{(i)}])=[\gamma _m^{(i)}]$
for all m and i. By Proposition 4.6, each
![]() $\gamma _m^{(i)}$
is homotopic to a dynamic ray
$\gamma _m^{(i)}$
is homotopic to a dynamic ray
![]() $g_m^{(i)}$
rel
$g_m^{(i)}$
rel
![]() $P(E_{\lambda })\cup \{\infty \}$
.
$P(E_{\lambda })\cup \{\infty \}$
.
Because the
![]() $\gamma _m^{(i)}$
as well as the
$\gamma _m^{(i)}$
as well as the
![]() $g_m^{(i)}$
are pairwise non-homotopic rel
$g_m^{(i)}$
are pairwise non-homotopic rel
![]() $P(E_{\lambda })\cup \{\infty \}$
and intersect each other at most at their endpoints, the two curve systems fulfill the hypotheses of Lemma 3.15. Thus, there exists an ambient isotopy
$P(E_{\lambda })\cup \{\infty \}$
and intersect each other at most at their endpoints, the two curve systems fulfill the hypotheses of Lemma 3.15. Thus, there exists an ambient isotopy
![]() $I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
rel
$I\colon \overline {\mathbb {C}}\times [0,1]\to \overline {\mathbb {C}}$
rel
![]() $P(E_{\lambda })\cup \{\infty \}$
satisfying
$P(E_{\lambda })\cup \{\infty \}$
satisfying
![]() $I^1(\gamma _m^{(i)})=g_m^{(i)}$
for all
$I^1(\gamma _m^{(i)})=g_m^{(i)}$
for all
![]() $m\in \{l+1,\ldots ,n\}$
and all
$m\in \{l+1,\ldots ,n\}$
and all
![]() $i\in \{1,\ldots ,d\}$
. By Lemma 3.10, the tree
$i\in \{1,\ldots ,d\}$
. By Lemma 3.10, the tree
![]() $H_{0}:=I^1(H)$
is again a homotopy Hubbard tree and it is equivalent to H.
$H_{0}:=I^1(H)$
is again a homotopy Hubbard tree and it is equivalent to H.
The last part of the proof works by induction. Assume that
![]() $H_j\cong H$
is equivalent to our initial homotopy Hubbard tree and for each post-singular point
$H_j\cong H$
is equivalent to our initial homotopy Hubbard tree and for each post-singular point
![]() $p\in P(E_{\lambda })$
, for which
$p\in P(E_{\lambda })$
, for which
![]() $E_{\lambda }^{\circ j}(p)$
is periodic and every access A to p in
$E_{\lambda }^{\circ j}(p)$
is periodic and every access A to p in
![]() $H_j$
, there exists a dynamic ray g approaching p through A. Choose a small neighborhood
$H_j$
, there exists a dynamic ray g approaching p through A. Choose a small neighborhood
![]() $V_j$
of
$V_j$
of
![]() $0$
such that
$0$
such that
![]() $V_j$
does not intersect the dynamic rays landing at the points
$V_j$
does not intersect the dynamic rays landing at the points
![]() $p_{l+1-j},\ldots ,p_n$
. The pre-image
$p_{l+1-j},\ldots ,p_n$
. The pre-image
![]() $U_l:=\widehat {E_{\lambda }}^{-1}(V_l)$
does not intersect any of the dynamic rays landing at the points
$U_l:=\widehat {E_{\lambda }}^{-1}(V_l)$
does not intersect any of the dynamic rays landing at the points
![]() $p_{l-j},\ldots ,p_n$
. By Lemma 3.13, there exists a tree
$p_{l-j},\ldots ,p_n$
. By Lemma 3.13, there exists a tree
![]() $H_{j}''\subset \mathbb {C}$
which is isotopic to
$H_{j}''\subset \mathbb {C}$
which is isotopic to
![]() $H_{j}'$
rel
$H_{j}'$
rel
![]() $\mathbb {C}_T\setminus U_j$
and isotopic to
$\mathbb {C}_T\setminus U_j$
and isotopic to
![]() $H_{j}$
rel
$H_{j}$
rel
![]() $P(E_{\lambda })$
in
$P(E_{\lambda })$
in
![]() $\mathbb {C}$
. By Lemma 3.10, the tree
$\mathbb {C}$
. By Lemma 3.10, the tree
![]() $H_{j+1}:=H_{j}''$
is itself a homotopy Hubbard tree and we have
$H_{j+1}:=H_{j}''$
is itself a homotopy Hubbard tree and we have
![]() $H_{j+1}\cong H_{j}\cong H$
. By construction, for every
$H_{j+1}\cong H_{j}\cong H$
. By construction, for every
![]() $p\in \{p_{l-j},\ldots ,p_n\}$
and every access to
$p\in \{p_{l-j},\ldots ,p_n\}$
and every access to
![]() $H_{j+1}$
at p, there exists a dynamic ray approaching p through this access. Iterating this procedure l times yields a tree
$H_{j+1}$
at p, there exists a dynamic ray approaching p through this access. Iterating this procedure l times yields a tree
![]() $\tilde {H}:=H_l$
satisfying the conditions of the theorem.
$\tilde {H}:=H_l$
satisfying the conditions of the theorem.
Corollary 4.10. (Equal kneading sequences)
Let H be a homotopy Hubbard tree for the post-singularly finite exponential map
![]() $E_{\lambda }$
, let
$E_{\lambda }$
, let
![]() $f\colon H\to H$
be an induced self-map of H, and let
$f\colon H\to H$
be an induced self-map of H, and let
![]() $v_T$
be the singular point of f. Two post-singular points
$v_T$
be the singular point of f. Two post-singular points
![]() $p,q\in P(E_{\lambda })$
are contained in the same branch of H at
$p,q\in P(E_{\lambda })$
are contained in the same branch of H at
![]() $v_T$
if and only if the first entries of the itineraries of p and q with respect to some, and hence any, dynamical partition (compare Lemma 4.1) are equal.
$v_T$
if and only if the first entries of the itineraries of p and q with respect to some, and hence any, dynamical partition (compare Lemma 4.1) are equal.
As this property is independent of the choice of H, different homotopy Hubbard trees yield exponential dynamical trees with equal kneading sequences.
Proof If
![]() $\tilde {H}\cong H$
and
$\tilde {H}\cong H$
and
![]() $\tilde {f}$
is an induced self-map of
$\tilde {f}$
is an induced self-map of
![]() $\tilde {H}$
, then there exists a homeomorphism
$\tilde {H}$
, then there exists a homeomorphism
![]() $\theta \colon H\to \tilde {H}$
that restricts to a conjugation between f and
$\theta \colon H\to \tilde {H}$
that restricts to a conjugation between f and
![]() $\tilde {f}$
on the set
$\tilde {f}$
on the set
![]() $V_f$
of marked points. This follows from the elaborations on different self-maps of the same tree after Definition 3.7 together with the proof of Lemma 3.10. As
$V_f$
of marked points. This follows from the elaborations on different self-maps of the same tree after Definition 3.7 together with the proof of Lemma 3.10. As
![]() $\theta $
maps branches of H at
$\theta $
maps branches of H at
![]() $v_T$
to branches of
$v_T$
to branches of
![]() $\tilde {H}$
at
$\tilde {H}$
at
![]() $\tilde {v_T}$
, it is enough to prove Corollary 4.10 for an equivalent homotopy Hubbard tree
$\tilde {v_T}$
, it is enough to prove Corollary 4.10 for an equivalent homotopy Hubbard tree
![]() $\tilde {H}$
.
$\tilde {H}$
.
By Proposition 4.9, there exist a dynamic ray g landing at
![]() $0$
and a homotopy Hubbard tree
$0$
and a homotopy Hubbard tree
![]() $\tilde {H}\cong H$
such that
$\tilde {H}\cong H$
such that
![]() $\operatorname {\mathrm {Tr}}(g)\cap \tilde {H}=\emptyset $
. Let
$\operatorname {\mathrm {Tr}}(g)\cap \tilde {H}=\emptyset $
. Let
![]() $\mathcal {D}$
be the dynamical partition with respect to g. Then we have
$\mathcal {D}$
be the dynamical partition with respect to g. Then we have
![]() $\tilde {H}'\cap \partial \mathcal {D}=\emptyset $
, where
$\tilde {H}'\cap \partial \mathcal {D}=\emptyset $
, where
![]() $\tilde {H}'$
is the subtree of the pre-image tree of
$\tilde {H}'$
is the subtree of the pre-image tree of
![]() $\tilde {H}$
spanned by
$\tilde {H}$
spanned by
![]() $P(E_{\lambda })$
. It follows that post-singular points from different sectors cannot be contained in the same branch of
$P(E_{\lambda })$
. It follows that post-singular points from different sectors cannot be contained in the same branch of
![]() $\tilde {H}'$
at
$\tilde {H}'$
at
![]() $-\infty $
. Furthermore, each partition sector contains at most one branch of
$-\infty $
. Furthermore, each partition sector contains at most one branch of
![]() $\tilde {H}'$
at
$\tilde {H}'$
at
![]() $-\infty $
, as the singular value is an endpoint of
$-\infty $
, as the singular value is an endpoint of
![]() $\tilde {H}$
by Lemma 4.3. Hence, p and q are contained in the same branch of
$\tilde {H}$
by Lemma 4.3. Hence, p and q are contained in the same branch of
![]() $\tilde {H}'$
at
$\tilde {H}'$
at
![]() $-\infty $
if and only if they are contained in the same sector of
$-\infty $
if and only if they are contained in the same sector of
![]() $\mathcal {D}$
, that is, if their itineraries start with the same integer. Branches of
$\mathcal {D}$
, that is, if their itineraries start with the same integer. Branches of
![]() $\tilde {H}'$
at
$\tilde {H}'$
at
![]() $-\infty $
get identified with branches of H at
$-\infty $
get identified with branches of H at
![]() $\tilde {v}_T$
, so the corollary follows.
$\tilde {v}_T$
, so the corollary follows.
We will now show that an exponential dynamical tree is already determined (up to equivalence) by its kneading sequence. The following ideas, leading to the proof of this fact, are inspired by and, in many parts, analogous to results of [Reference Bruin, Kaffl and SchleicherBKS]. Let us start with a simple observation.
Proposition 4.11. (Distinct itineraries)
Let
![]() $(H,f,B_{k_i})$
be an exponential dynamical tree and let
$(H,f,B_{k_i})$
be an exponential dynamical tree and let
![]() $p,q\in V_f$
be distinct marked points. Then
$p,q\in V_f$
be distinct marked points. Then
![]() $\operatorname {\mathrm {It}}(p)\neq \operatorname {\mathrm {It}}(q)$
.
$\operatorname {\mathrm {It}}(p)\neq \operatorname {\mathrm {It}}(q)$
.
Proof We write
![]() $\operatorname {\mathrm {It}}(p)=\mathtt {p_1 p_2\ldots }$
and
$\operatorname {\mathrm {It}}(p)=\mathtt {p_1 p_2\ldots }$
and
![]() $\operatorname {\mathrm {It}}(q)=\mathtt {q_1 q_2\ldots }$
. If
$\operatorname {\mathrm {It}}(q)=\mathtt {q_1 q_2\ldots }$
. If
![]() $\mathtt {p_1}\neq \mathtt {q_1}$
, we are done. Else, we have
$\mathtt {p_1}\neq \mathtt {q_1}$
, we are done. Else, we have
![]() $\mathtt {p_1}=\mathtt {q_1}=k_1$
, and hence
$\mathtt {p_1}=\mathtt {q_1}=k_1$
, and hence
![]() $p,q\in B_{k_1}$
for the branch
$p,q\in B_{k_1}$
for the branch
![]() $B_{k_1}$
of H at
$B_{k_1}$
of H at
![]() $v_T$
. By Lemma 4.3, the restriction
$v_T$
. By Lemma 4.3, the restriction
![]() $f|_{B_{k_1}}$
is injective, so we have
$f|_{B_{k_1}}$
is injective, so we have
![]() $f([p,q])=[f(p),f(q)]$
. By expansivity of
$f([p,q])=[f(p),f(q)]$
. By expansivity of
![]() $(H,f)$
, there exists a smallest
$(H,f)$
, there exists a smallest
![]() $n\geq 0$
, such that
$n\geq 0$
, such that
![]() $v_T\in f^{\circ n}([p,q])=[f^{\circ n}(p),f^{\circ n}(q)]$
. Therefore, the itineraries
$v_T\in f^{\circ n}([p,q])=[f^{\circ n}(p),f^{\circ n}(q)]$
. Therefore, the itineraries
![]() $\operatorname {\mathrm {It}}(f^{\circ n}(p))$
and
$\operatorname {\mathrm {It}}(f^{\circ n}(p))$
and
![]() $\operatorname {\mathrm {It}}(f^{\circ n}(q))$
have different initial entries.
$\operatorname {\mathrm {It}}(f^{\circ n}(q))$
have different initial entries.
Let
![]() $(H,f,B_{k_i})$
be an exponential dynamical tree and let
$(H,f,B_{k_i})$
be an exponential dynamical tree and let
![]() $p,q,r\in V_f$
be distinct marked points. The subtree
$p,q,r\in V_f$
be distinct marked points. The subtree
![]() $[p,q,r]$
spanned by p, q, and r is called a triod. It must look in one of two ways: if
$[p,q,r]$
spanned by p, q, and r is called a triod. It must look in one of two ways: if
![]() $[p,q,r]$
is homeomorphic to the letter Y, we call it branched. Else, it is homeomorphic to the letter I and we call it linear. It should now be clear how to define the middle point
$[p,q,r]$
is homeomorphic to the letter Y, we call it branched. Else, it is homeomorphic to the letter I and we call it linear. It should now be clear how to define the middle point
![]() $b[p,q,r]\in H$
of the triod
$b[p,q,r]\in H$
of the triod
![]() $[p,q,r]$
. Note that the middle point
$[p,q,r]$
. Note that the middle point
![]() $b[p,q,r]\in V_f$
is also a marked point.
$b[p,q,r]\in V_f$
is also a marked point.
The shape of the triod
![]() $[p,q,r]$
as well as the itinerary of the middle point
$[p,q,r]$
as well as the itinerary of the middle point
![]() $b[p,q,r]$
can be determined algorithmically from the itineraries of the marked points p, q, and r. This algorithm is known as the triod algorithm. The triod algorithm is purely combinatorical and could be applied to any triple of pre-periodic sequences (not just the itineraries of p, q, and r). We apply it only to itineraries of vertices of an abstract exponential tree
$b[p,q,r]$
can be determined algorithmically from the itineraries of the marked points p, q, and r. This algorithm is known as the triod algorithm. The triod algorithm is purely combinatorical and could be applied to any triple of pre-periodic sequences (not just the itineraries of p, q, and r). We apply it only to itineraries of vertices of an abstract exponential tree
![]() $(H, f, B_{k_i})$
; let
$(H, f, B_{k_i})$
; let
![]() $\nu $
be its kneading sequence.
$\nu $
be its kneading sequence.
Definition 4.12. (Formal triods and the formal triod map)
Let
![]() $\star $
be a formal symbol not contained in
$\star $
be a formal symbol not contained in
![]() $\mathbb {Z}$
. The space of formal (pre-)periodic points
$\mathbb {Z}$
. The space of formal (pre-)periodic points
![]() $\mathcal {S}_\nu \subset (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
consists of all (pre-)periodic sequences
$\mathcal {S}_\nu \subset (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
consists of all (pre-)periodic sequences
![]() $\mathtt {\underline {t}}\in (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
such that either
$\mathtt {\underline {t}}\in (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
such that either
![]() $\mathtt {\underline {t}}\in \mathbb {Z}^{\mathbb {N}}$
and
$\mathtt {\underline {t}}\in \mathbb {Z}^{\mathbb {N}}$
and
![]() $\sigma ^{\circ n}(\mathtt {\mathtt {\underline {t}}})\neq \nu $
for all
$\sigma ^{\circ n}(\mathtt {\mathtt {\underline {t}}})\neq \nu $
for all
![]() $n\in \mathbb {N}$
or
$n\in \mathbb {N}$
or
![]() $\mathtt {\underline {t}}$
is contained in the backwards orbit
$\mathtt {\underline {t}}$
is contained in the backwards orbit
of finite integer sequences followed by
![]() $\star \nu $
. We call a point
$\star \nu $
. We call a point
![]() $\mathtt {\underline {t}}\in \mathcal {S}_\nu $
a pre-singular point if
$\mathtt {\underline {t}}\in \mathcal {S}_\nu $
a pre-singular point if
![]() $\mathtt {\underline {t}}\in \Omega ^-(\star \nu )$
.
$\mathtt {\underline {t}}\in \Omega ^-(\star \nu )$
.
We have the shift map
![]() $\sigma \colon (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}\to (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
acting on the full space of sequences. Note that we are using the same symbol for the shift map on
$\sigma \colon (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}\to (\mathbb {Z}\cup \{\star \})^{\mathbb {N}}$
acting on the full space of sequences. Note that we are using the same symbol for the shift map on
![]() $\mathcal {S}$
. It will always be clear from the context which map we are considering.
$\mathcal {S}$
. It will always be clear from the context which map we are considering.
Any triple of distinct sequences
![]() $\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\in \mathcal {S}_\nu $
is called a formal triod
$\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\in \mathcal {S}_\nu $
is called a formal triod
![]() $\mathtt {[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]}$
. Given a formal triod, we define the formal triod map
$\mathtt {[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]}$
. Given a formal triod, we define the formal triod map
![]() $\mathcal {T}$
as follows:
$\mathcal {T}$
as follows:
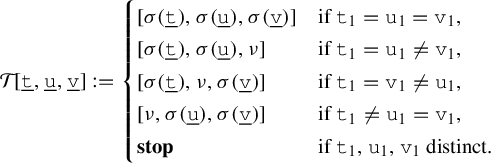 $$ \begin{align*} \mathcal{T}[\mathtt{\underline{t}},\mathtt{\underline{u}},\mathtt{\underline{v}}]:= \begin{cases} [\sigma(\mathtt{\underline{t}}), \sigma(\mathtt{\underline{u}}), \sigma(\mathtt{\underline{v}})] &\text{if } \mathtt{t}_1=\mathtt{u}_1=\mathtt{v}_1,\\ [\sigma(\mathtt{\underline{t}}), \sigma(\mathtt{\underline{u}}), \nu] &\text{if } \mathtt{t}_1=\mathtt{u}_1\neq \mathtt{v}_1,\\ [\sigma(\mathtt{\underline{t}}), \nu, \sigma(\mathtt{\underline{v}})] &\text{if } \mathtt{t}_1=\mathtt{v}_1\neq \mathtt{u}_1,\\ [\nu, \sigma(\mathtt{\underline{u}}), \sigma(\mathtt{\underline{v}})] &\text{if } \mathtt{t}_1\neq \mathtt{u}_1=\mathtt{v}_1,\\ \textbf{stop} &\text{if } \mathtt{t}_1, \mathtt{u}_1, \mathtt{v}_1 \text{ distinct}.\end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{T}[\mathtt{\underline{t}},\mathtt{\underline{u}},\mathtt{\underline{v}}]:= \begin{cases} [\sigma(\mathtt{\underline{t}}), \sigma(\mathtt{\underline{u}}), \sigma(\mathtt{\underline{v}})] &\text{if } \mathtt{t}_1=\mathtt{u}_1=\mathtt{v}_1,\\ [\sigma(\mathtt{\underline{t}}), \sigma(\mathtt{\underline{u}}), \nu] &\text{if } \mathtt{t}_1=\mathtt{u}_1\neq \mathtt{v}_1,\\ [\sigma(\mathtt{\underline{t}}), \nu, \sigma(\mathtt{\underline{v}})] &\text{if } \mathtt{t}_1=\mathtt{v}_1\neq \mathtt{u}_1,\\ [\nu, \sigma(\mathtt{\underline{u}}), \sigma(\mathtt{\underline{v}})] &\text{if } \mathtt{t}_1\neq \mathtt{u}_1=\mathtt{v}_1,\\ \textbf{stop} &\text{if } \mathtt{t}_1, \mathtt{u}_1, \mathtt{v}_1 \text{ distinct}.\end{cases} \end{align*} $$
In all cases other than the stop case,
![]() $\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is again a formal triod: because
$\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is again a formal triod: because
![]() $\mathcal {S}_\nu $
is forward invariant under
$\mathcal {S}_\nu $
is forward invariant under
![]() $\sigma $
and
$\sigma $
and
![]() $\nu \in \mathcal {S}_\nu $
, the three image sequences are contained in
$\nu \in \mathcal {S}_\nu $
, the three image sequences are contained in
![]() $\mathcal {S}_\nu $
and they are distinct, as we have
$\mathcal {S}_\nu $
and they are distinct, as we have
![]() $\{\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\}\cap \{k\nu ~\vert ~k\in \mathbb {Z}\}=\emptyset $
. By construction, the only sequence that starts with
$\{\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\}\cap \{k\nu ~\vert ~k\in \mathbb {Z}\}=\emptyset $
. By construction, the only sequence that starts with
![]() $\star $
is
$\star $
is
![]() $\star \nu $
, so in all cases other than the stop case, at least two of the first entries of the involved sequences are equal integers. If exactly two of the three first entries are equal, we say that the sequence whose first entry differs from the other two gets chopped off under iteration of
$\star \nu $
, so in all cases other than the stop case, at least two of the first entries of the involved sequences are equal integers. If exactly two of the three first entries are equal, we say that the sequence whose first entry differs from the other two gets chopped off under iteration of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
The formal triod map can be iterated as long as the stop case is not reached. We write
![]() $\mathcal {T}^{{\kern1.5pt}\circ n}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
for the resulting formal triod after n iterations of
$\mathcal {T}^{{\kern1.5pt}\circ n}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
for the resulting formal triod after n iterations of
![]() $\mathcal {T}$
(if iteration is possible). Note that if the triod can be iterated indefinitely, at least two sequences each get chopped off under iteration of
$\mathcal {T}$
(if iteration is possible). Note that if the triod can be iterated indefinitely, at least two sequences each get chopped off under iteration of
![]() $\mathcal {T}$
infinitely many times: otherwise, there would exist an
$\mathcal {T}$
infinitely many times: otherwise, there would exist an
![]() $n\in \mathbb {N}$
such that two of the three sequences of the triod
$n\in \mathbb {N}$
such that two of the three sequences of the triod
![]() $\mathcal {T}^{{\kern1.5pt}\circ n}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
never get chopped off. However, this implies that these sequences are equal, which contradicts the fact that all three sequences stay distinct under iteration of
$\mathcal {T}^{{\kern1.5pt}\circ n}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
never get chopped off. However, this implies that these sequences are equal, which contradicts the fact that all three sequences stay distinct under iteration of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Definition 4.13. (Majority vote and middle point of a formal triod)
Let
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
be a formal triod. If
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
be a formal triod. If
![]() $\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]\neq \textbf {stop}$
, then, as noted above, at least two of the three sequences start with the same integer. We denote this integer by
$\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]\neq \textbf {stop}$
, then, as noted above, at least two of the three sequences start with the same integer. We denote this integer by
![]() $\mathtt {m}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
and call it the majority vote of the triod
$\mathtt {m}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
and call it the majority vote of the triod
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
. Let
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
. Let
![]() $i_0\in \mathbb {N}_0$
be chosen such that
$i_0\in \mathbb {N}_0$
be chosen such that
![]() $\mathcal {T}^{{\kern1.5pt}\circ i_0}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]=\textbf {stop}$
, if the triod eventually reaches the stop case, and let
$\mathcal {T}^{{\kern1.5pt}\circ i_0}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]=\textbf {stop}$
, if the triod eventually reaches the stop case, and let
![]() $i_0=\infty $
otherwise. We define a sequence
$i_0=\infty $
otherwise. We define a sequence
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
by setting
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
by setting
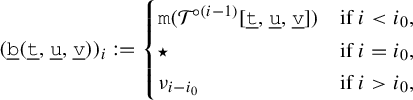 $$ \begin{align*} (\mathtt{\underline{b}}(\mathtt{\underline{t}},\mathtt{\underline{u}},\mathtt{\underline{v}}))_i:= \begin{cases} \mathtt{m}(\mathcal{T}^{\circ (i-1)}[\mathtt{\underline{t}},\mathtt{\underline{u}},\mathtt{\underline{v}}])&\text{if}~i<i_0,\\ \star&\text{if}~i=i_0,\\ \nu_{i-i_0}&\text{if}~i>i_0, \end{cases} \end{align*} $$
$$ \begin{align*} (\mathtt{\underline{b}}(\mathtt{\underline{t}},\mathtt{\underline{u}},\mathtt{\underline{v}}))_i:= \begin{cases} \mathtt{m}(\mathcal{T}^{\circ (i-1)}[\mathtt{\underline{t}},\mathtt{\underline{u}},\mathtt{\underline{v}}])&\text{if}~i<i_0,\\ \star&\text{if}~i=i_0,\\ \nu_{i-i_0}&\text{if}~i>i_0, \end{cases} \end{align*} $$
and we call
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
the middle point of the triod. If we have
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
the middle point of the triod. If we have
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})\notin \{\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\}$
, we call
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})\notin \{\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\}$
, we call
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
branched, otherwise we call it linear. Sometimes, we want to be more precise and call a triod pre-singularly branched or pre-singularly linear if
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
branched, otherwise we call it linear. Sometimes, we want to be more precise and call a triod pre-singularly branched or pre-singularly linear if
![]() $i_0<\infty $
, that is, if it eventually reaches the stop case under iteration of the triod map.
$i_0<\infty $
, that is, if it eventually reaches the stop case under iteration of the triod map.
We now prove that the triod algorithm really determines the itineraries of the branch points of an exponential dynamical tree. The proof is an adaption of [Reference Bruin, Kaffl and SchleicherBKS, Proposition 3.5].
Lemma 4.14. (Correctness of the triod algorithm)
Let
![]() $(H,f,B_{k_i})$
be an exponential dynamical tree and let
$(H,f,B_{k_i})$
be an exponential dynamical tree and let
![]() $[p_1,p_2,p_3]\subset H$
be a triod. Then
$[p_1,p_2,p_3]\subset H$
be a triod. Then
![]() $[p_1,p_2,p_3]$
is branched if and only if the formal triod
$[p_1,p_2,p_3]$
is branched if and only if the formal triod
![]() $[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is branched. Furthermore, we have
$[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is branched. Furthermore, we have
Proof If
![]() $p_1$
,
$p_1$
,
![]() $p_2$
, and
$p_2$
, and
![]() $p_3$
are contained in distinct branches of H at
$p_3$
are contained in distinct branches of H at
![]() $v_T$
, then
$v_T$
, then
![]() $b[p_1,p_2,p_3]=v_T$
, and this is the branch point determined (on the level of itineraries) by the triod algorithm. If one of the
$b[p_1,p_2,p_3]=v_T$
, and this is the branch point determined (on the level of itineraries) by the triod algorithm. If one of the
![]() $p_i$
equals
$p_i$
equals
![]() $v_T$
and the other two points are contained in different branches of H, then
$v_T$
and the other two points are contained in different branches of H, then
![]() $b[p_1,p_2,p_3]=p_i$
, and again this is the output of the triod algorithm.
$b[p_1,p_2,p_3]=p_i$
, and again this is the output of the triod algorithm.
If both of these cases do not occur, there exist a branch
![]() $B_{k_1}$
of H at
$B_{k_1}$
of H at
![]() $v_T$
and distinct indices
$v_T$
and distinct indices
![]() $i,j\in \{1,2,3\}$
, such that
$i,j\in \{1,2,3\}$
, such that
![]() $p_i,p_j\in B_{k_1}\setminus \{v_t\}$
. Hence, we also have
$p_i,p_j\in B_{k_1}\setminus \{v_t\}$
. Hence, we also have
![]() $b[p_1,p_2,p_3]\in B_{k_1}\setminus \{v_T\}$
. We see, that the first entry of
$b[p_1,p_2,p_3]\in B_{k_1}\setminus \{v_T\}$
. We see, that the first entry of
![]() $\operatorname {\mathrm {It}}(b[p_1,p_2,p_3])$
is calculated correctly by the triod algorithm.
$\operatorname {\mathrm {It}}(b[p_1,p_2,p_3])$
is calculated correctly by the triod algorithm.
If all of the
![]() $p_l$
are contained in
$p_l$
are contained in
![]() $B_{k_1}$
, the spanned subtree
$B_{k_1}$
, the spanned subtree
![]() $[p_1,p_2,p_3]$
is also entirely contained in
$[p_1,p_2,p_3]$
is also entirely contained in
![]() $B_{k_1}$
. By Lemma 4.3, the restriction
$B_{k_1}$
. By Lemma 4.3, the restriction
![]() $f|_{[p_1,p_2,p_3]}$
is injective, so
$f|_{[p_1,p_2,p_3]}$
is injective, so
![]() $[f(p_1),f(p_2),f(p_3)]$
is also a triod and we have
$[f(p_1),f(p_2),f(p_3)]$
is also a triod and we have
![]() $b[f(p_1),f(p_2),f(p_3)]=f(b[p_1,p_2,p_3])$
. On the level of formal triods, we have
$b[f(p_1),f(p_2),f(p_3)]=f(b[p_1,p_2,p_3])$
. On the level of formal triods, we have
![]() $\mathcal {T}{\kern1.5pt}[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]=[\operatorname {\mathrm {It}}(f(p_1)),\operatorname {\mathrm {It}}(f(p_2)),\operatorname {\mathrm {It}}(f(p_3))]$
. If instead
$\mathcal {T}{\kern1.5pt}[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]=[\operatorname {\mathrm {It}}(f(p_1)),\operatorname {\mathrm {It}}(f(p_2)),\operatorname {\mathrm {It}}(f(p_3))]$
. If instead
![]() $p_l\notin B_{k_1}$
, while
$p_l\notin B_{k_1}$
, while
![]() $p_i,p_j\in B_{k_1}$
, then the chopped-off triod
$p_i,p_j\in B_{k_1}$
, then the chopped-off triod
![]() $[v_T, p_i, p_j]$
still gets mapped forward injectively. Hence, we have
$[v_T, p_i, p_j]$
still gets mapped forward injectively. Hence, we have
![]() $b[0,f(p_i),f(p_j)]=f(b[p_1,p_2,p_3])$
. On the level of formal triods, we have
$b[0,f(p_i),f(p_j)]=f(b[p_1,p_2,p_3])$
. On the level of formal triods, we have
![]() $\mathcal {T}{\kern1.5pt}[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]=[\operatorname {\mathrm {It}}(0),\operatorname {\mathrm {It}}(f(p_i)),\operatorname {\mathrm {It}}(f(p_j))]$
.
$\mathcal {T}{\kern1.5pt}[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]=[\operatorname {\mathrm {It}}(0),\operatorname {\mathrm {It}}(f(p_i)),\operatorname {\mathrm {It}}(f(p_j))]$
.
If we are in one of the two preceding cases (we have not reached the stop case in the first iteration step), we apply the same reasoning as before to the image triod. Hence, the triod algorithm correctly calculates
![]() $\operatorname {\mathrm {It}}(b[p_1,p_2,p_3])$
. It remains to show that
$\operatorname {\mathrm {It}}(b[p_1,p_2,p_3])$
. It remains to show that
![]() $[p_1,p_2,p_3]$
is branched if and only if the formal triod
$[p_1,p_2,p_3]$
is branched if and only if the formal triod
![]() $[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is branched. If
$[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is branched. If
![]() $[p_1,p_2,p_3]$
is branched, then
$[p_1,p_2,p_3]$
is branched, then
by Proposition 4.11, so the formal triod
![]() $[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is also branched. If
$[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is also branched. If
![]() $[p_1,p_2,p_3]$
is linear, then
$[p_1,p_2,p_3]$
is linear, then
so the formal triod
![]() $[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is also linear.
$[\operatorname {\mathrm {It}}(p_1),\operatorname {\mathrm {It}}(p_2),\operatorname {\mathrm {It}}(p_3)]$
is also linear.
Proof of Theorem 4.4
It remains to show that two exponential dynamical trees
![]() $(H,f,B_{k_i})$
and
$(H,f,B_{k_i})$
and
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
with the same kneading sequence are equivalent. Because every endpoint of H is a post-singular point, every branch point of H is also the branch point of a post-singular triod. Thus, the kneading sequence fully determines the itineraries of all marked points of H and for every triod
$(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
with the same kneading sequence are equivalent. Because every endpoint of H is a post-singular point, every branch point of H is also the branch point of a post-singular triod. Thus, the kneading sequence fully determines the itineraries of all marked points of H and for every triod
![]() $[p,q,r]$
of marked points, it determines their incidence relation by Lemma 4.14. As
$[p,q,r]$
of marked points, it determines their incidence relation by Lemma 4.14. As
![]() $(H,f,B_{k_i})$
and
$(H,f,B_{k_i})$
and
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
have the same kneading sequence, their marked points have the same itineraries, and we can define a homeomorphism
$(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
have the same kneading sequence, their marked points have the same itineraries, and we can define a homeomorphism
![]() $\varphi \colon H\to \tilde {H}$
by sending the marked points of
$\varphi \colon H\to \tilde {H}$
by sending the marked points of
![]() $(H,f,B_{k_i})$
to the marked points of
$(H,f,B_{k_i})$
to the marked points of
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
with the same itinerary and extending this map to the edges between the marked points. The exponential dynamical trees
$(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
with the same itinerary and extending this map to the edges between the marked points. The exponential dynamical trees
![]() $(H,f,B_{k_i})$
and
$(H,f,B_{k_i})$
and
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
are equivalent via
$(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
are equivalent via
![]() $\varphi $
.
$\varphi $
.
Theorem 4.4 is an important step in proving uniqueness of homotopy Hubbard trees, but we still have to see that the embedding of the tree into the plane is also unique. Let H be a homotopy Hubbard tree and let
![]() $[p,q,r]$
be a triod of post-singular points. If
$[p,q,r]$
be a triod of post-singular points. If
![]() $[p,q,r]$
is linear with middle point p, Proposition 4.9 implies that there are two dynamic rays
$[p,q,r]$
is linear with middle point p, Proposition 4.9 implies that there are two dynamic rays
![]() $g_{\underline {p}},g_{\underline {p}'}$
landing at p and separating q from r in the sense that q and r are contained in different connected components of
$g_{\underline {p}},g_{\underline {p}'}$
landing at p and separating q from r in the sense that q and r are contained in different connected components of
![]() $\mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {p}})\cup \operatorname {\mathrm {Tr}}(g_{\underline {p}'})\cup \{p\}$
. Conversely, if such separating rays exist, the triod
$\mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {p}})\cup \operatorname {\mathrm {Tr}}(g_{\underline {p}'})\cup \{p\}$
. Conversely, if such separating rays exist, the triod
![]() $[p,q,r]$
is linear with middle point p.
$[p,q,r]$
is linear with middle point p.
Lemma 4.15. (Separating rays determine triod type)
Let H be a homotopy Hubbard tree and let
![]() $[p,q,r]$
be a triod of post-singular points. If there are two dynamic rays
$[p,q,r]$
be a triod of post-singular points. If there are two dynamic rays
![]() $g_{\underline {p}},g_{\underline {p}'}$
landing at p, such that q and r are contained in different connected components of
$g_{\underline {p}},g_{\underline {p}'}$
landing at p, such that q and r are contained in different connected components of
![]() $\mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {p}})\cup \operatorname {\mathrm {Tr}}(g_{\underline {p}'})\cup \{p\})$
, the triod
$\mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {p}})\cup \operatorname {\mathrm {Tr}}(g_{\underline {p}'})\cup \{p\})$
, the triod
![]() $[p,q,r]$
is linear with middle point p.
$[p,q,r]$
is linear with middle point p.
Proof Let
![]() $\operatorname {\mathrm {It}}(p)=\mathtt {\underline {p}}=\mathtt {p_1 p_2\ldots\,}$
,
$\operatorname {\mathrm {It}}(p)=\mathtt {\underline {p}}=\mathtt {p_1 p_2\ldots\,}$
,
![]() $\operatorname {\mathrm {It}}(q)=\mathtt {\underline {q}}=\mathtt {q_1 q_2\ldots }$
, and
$\operatorname {\mathrm {It}}(q)=\mathtt {\underline {q}}=\mathtt {q_1 q_2\ldots }$
, and
![]() $\operatorname {\mathrm {It}}(r)=\mathtt {\underline {r}}=\mathtt {r_1 r_2\ldots }$
be the itineraries of the points p, q, and r. By correctness of the triod algorithm (see Lemma 4.14), it is enough to show that
$\operatorname {\mathrm {It}}(r)=\mathtt {\underline {r}}=\mathtt {r_1 r_2\ldots }$
be the itineraries of the points p, q, and r. By correctness of the triod algorithm (see Lemma 4.14), it is enough to show that
![]() $\mathtt {\underline {b}}(\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}})=\mathtt {\underline {p}}$
.
$\mathtt {\underline {b}}(\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}})=\mathtt {\underline {p}}$
.
By Proposition 2.13 and Theorem 2.10, there exist addresses
![]() $\underline {q}$
and
$\underline {q}$
and
![]() $\underline {r}$
satisfying
$\underline {r}$
satisfying
![]() $\operatorname {\mathrm {It}}(\underline {q}~\vert ~\underline {s})=\mathtt {\underline {q}}$
and
$\operatorname {\mathrm {It}}(\underline {q}~\vert ~\underline {s})=\mathtt {\underline {q}}$
and
![]() $\operatorname {\mathrm {It}}(\underline {r}~\vert ~\underline {s})=\mathtt {\underline {r}}$
. The triod
$\operatorname {\mathrm {It}}(\underline {r}~\vert ~\underline {s})=\mathtt {\underline {r}}$
. The triod
![]() $[\underline {p},\underline {q},\underline {r}]$
is called a triod of external addresses associated to
$[\underline {p},\underline {q},\underline {r}]$
is called a triod of external addresses associated to
![]() $[\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}}]$
(this terminology is introduced rigorously in §5). It will be shown in §5 that
$[\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}}]$
(this terminology is introduced rigorously in §5). It will be shown in §5 that
![]() $[\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}}]$
has the same shape as the triod
$[\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}}]$
has the same shape as the triod
![]() $[\underline {p},\underline {q},\underline {r}]$
of associated external addresses. Finally, Lemma 5.8 implies that
$[\underline {p},\underline {q},\underline {r}]$
of associated external addresses. Finally, Lemma 5.8 implies that
![]() $\mathtt {\underline {b}}(\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}})=\mathtt {\underline {p}}$
.
$\mathtt {\underline {b}}(\mathtt {\underline {p}},\mathtt {\underline {q}},\mathtt {\underline {r}})=\mathtt {\underline {p}}$
.
We are now in the position to prove uniqueness of homotopy Hubbard trees.
Theorem 4.16. (Uniqueness of exponential Hubbard trees)
Let H and
![]() $\tilde {H}$
be homotopy Hubbard trees for the post-singularly finite exponential map
$\tilde {H}$
be homotopy Hubbard trees for the post-singularly finite exponential map
![]() $E_{\lambda }$
. Then H and
$E_{\lambda }$
. Then H and
![]() $\tilde {H}$
are homotopic relative to the post-singular set
$\tilde {H}$
are homotopic relative to the post-singular set
![]() $P(E_{\lambda })$
.
$P(E_{\lambda })$
.
Proof Let
![]() $P(E_{\lambda }){\kern2pt{=}\kern2pt}\{p_0{\kern2pt{=}\kern2pt}0, p_1{\kern2pt{=}\kern2pt}E_{\lambda }(p_0), \ldots , p_n{\kern2pt{=}\kern2pt}E_{\lambda }^{\circ n}(0), p_{n+1}{\kern2pt{=}\kern2pt}p_{l+1}\}$
denote the post-singular orbit of
$P(E_{\lambda }){\kern2pt{=}\kern2pt}\{p_0{\kern2pt{=}\kern2pt}0, p_1{\kern2pt{=}\kern2pt}E_{\lambda }(p_0), \ldots , p_n{\kern2pt{=}\kern2pt}E_{\lambda }^{\circ n}(0), p_{n+1}{\kern2pt{=}\kern2pt}p_{l+1}\}$
denote the post-singular orbit of
![]() $E_{\lambda }$
. At every post-singular point
$E_{\lambda }$
. At every post-singular point
![]() $p_i$
, the trees H and
$p_i$
, the trees H and
![]() $\tilde {H}$
have the same number of branches by Theorem 4.4; denote this number by
$\tilde {H}$
have the same number of branches by Theorem 4.4; denote this number by
![]() $d_i$
. By Proposition 4.9, we can assume without loss of generality that there are dynamic rays
$d_i$
. By Proposition 4.9, we can assume without loss of generality that there are dynamic rays
![]() $g_1^{(i)},\ldots , g_{d_i}^{(i)}$
landing at
$g_1^{(i)},\ldots , g_{d_i}^{(i)}$
landing at
![]() $p_i$
indexed according to their cyclic order at
$p_i$
indexed according to their cyclic order at
![]() $p_i$
and satisfying
$p_i$
and satisfying
![]() $H\cap \operatorname {\mathrm {Tr}}(g_l^{(i)})=\emptyset $
such that
$H\cap \operatorname {\mathrm {Tr}}(g_l^{(i)})=\emptyset $
such that
![]() $[p_i,p_j,p_k]_H$
is linear with middle point
$[p_i,p_j,p_k]_H$
is linear with middle point
![]() $p_i$
if and only if
$p_i$
if and only if
![]() $p_j$
and
$p_j$
and
![]() $p_k$
are contained in different connected components of
$p_k$
are contained in different connected components of
![]() $\mathbb {C}\setminus ((\cup _l\operatorname {\mathrm {Tr}}(g_l^{(i)}))\cup \{p_i\})$
. In the same way, we choose rays
$\mathbb {C}\setminus ((\cup _l\operatorname {\mathrm {Tr}}(g_l^{(i)}))\cup \{p_i\})$
. In the same way, we choose rays
![]() $\gamma _l^{(i)}$
for
$\gamma _l^{(i)}$
for
![]() $\tilde {H}$
, and we claim that (possibly after re-indexing)
$\tilde {H}$
, and we claim that (possibly after re-indexing)
![]() $g_l^{(i)}$
is homotopic to
$g_l^{(i)}$
is homotopic to
![]() $\gamma _l^{(i)}$
rel
$\gamma _l^{(i)}$
rel
![]() $P(E_{\lambda })$
.
$P(E_{\lambda })$
.
Otherwise, there are indices
![]() $i_0$
and
$i_0$
and
![]() $l_0$
such that
$l_0$
such that
![]() $\gamma _{l_0}^{(i_0)}$
is not homotopic to any of the rays
$\gamma _{l_0}^{(i_0)}$
is not homotopic to any of the rays
![]() $g_l^{(i_0)}$
. There is an index
$g_l^{(i_0)}$
. There is an index
![]() $l'$
such that
$l'$
such that
![]() $ g_{l'}^{(i_0)}\prec \gamma _{l_0}^{(i_0)}\prec g_{l'+1}^{(i_0)}$
holds. Furthermore, there are rays
$ g_{l'}^{(i_0)}\prec \gamma _{l_0}^{(i_0)}\prec g_{l'+1}^{(i_0)}$
holds. Furthermore, there are rays
![]() $g_{l_j}^{(j)}$
and
$g_{l_j}^{(j)}$
and
![]() $g_{l_k}^{(k)}$
landing at distinct post-singular points
$g_{l_k}^{(k)}$
landing at distinct post-singular points
![]() $p_j$
and
$p_j$
and
![]() $p_k$
different from
$p_k$
different from
![]() $p_{i_0}$
such that
$p_{i_0}$
such that
![]() $ g_{l'}^{(i_0)}\prec g_{l_j}^{(j)}\prec \gamma _{l_0}^{(i_0)}$
and
$ g_{l'}^{(i_0)}\prec g_{l_j}^{(j)}\prec \gamma _{l_0}^{(i_0)}$
and
![]() $ \gamma _{l_0}^{(i_0)}\prec g_{l_k}^{(k)}\prec g_{l'+1}^{(i_0)}$
hold; otherwise,
$ \gamma _{l_0}^{(i_0)}\prec g_{l_k}^{(k)}\prec g_{l'+1}^{(i_0)}$
hold; otherwise,
![]() $\gamma _{l_0}^{(i_0)}$
would either be homotopic to
$\gamma _{l_0}^{(i_0)}$
would either be homotopic to
![]() $g_{l'}^{(i_0)}$
or to
$g_{l'}^{(i_0)}$
or to
![]() $g_{l'+1}^{(i_0)}$
. However, then
$g_{l'+1}^{(i_0)}$
. However, then
![]() $p_j$
and
$p_j$
and
![]() $p_k$
are separated by
$p_k$
are separated by
![]() $\gamma _{l_0}^{(i_0)}$
and
$\gamma _{l_0}^{(i_0)}$
and
![]() $g_{l'}^{(i_0)}$
, so
$g_{l'}^{(i_0)}$
, so
![]() $[p_{i_0},p_j,p_k]$
is linear with middle point
$[p_{i_0},p_j,p_k]$
is linear with middle point
![]() $p_{i_0}$
by Lemma 4.15, which yields a contradiction.
$p_{i_0}$
by Lemma 4.15, which yields a contradiction.
By Proposition 4.6, homotopic dynamic rays landing together at a periodic post-singular point are equal, so we actually have
![]() $\gamma _l^{(i)}=g_l^{(i)}$
for all
$\gamma _l^{(i)}=g_l^{(i)}$
for all
![]() $i\in \{l+1,\ldots , n\}$
. The argument in the preceding paragraph also shows that the number of rays landing at
$i\in \{l+1,\ldots , n\}$
. The argument in the preceding paragraph also shows that the number of rays landing at
![]() $p_i$
equals
$p_i$
equals
![]() $d_i$
. Analyzing the proof of Proposition 4.9, we conclude that we can choose H and
$d_i$
. Analyzing the proof of Proposition 4.9, we conclude that we can choose H and
![]() $\tilde {H}$
as to not intersect any dynamic ray landing at any post-singular point (periodic or not). In particular, we can find a ray g landing at
$\tilde {H}$
as to not intersect any dynamic ray landing at any post-singular point (periodic or not). In particular, we can find a ray g landing at
![]() $0$
such that
$0$
such that
![]() $H\cap E_{\lambda }^{\circ i}(\operatorname {\mathrm {Tr}}(g))=\tilde {H}\cap E_{\lambda }^{\circ i}(\operatorname {\mathrm {Tr}}(g))=\emptyset $
for all
$H\cap E_{\lambda }^{\circ i}(\operatorname {\mathrm {Tr}}(g))=\tilde {H}\cap E_{\lambda }^{\circ i}(\operatorname {\mathrm {Tr}}(g))=\emptyset $
for all
![]() $i\in \{0,\ldots , n\}$
. Let
$i\in \{0,\ldots , n\}$
. Let
![]() $\varphi \colon \mathbb {D}\to \mathbb {C}\setminus \cup _i(E_{\lambda }^{\circ i}(\operatorname {\mathrm {Tr}}(g))\cup \{p_i\})$
be a conformal map. By Carathéodory’s theorem,
$\varphi \colon \mathbb {D}\to \mathbb {C}\setminus \cup _i(E_{\lambda }^{\circ i}(\operatorname {\mathrm {Tr}}(g))\cup \{p_i\})$
be a conformal map. By Carathéodory’s theorem,
![]() $\varphi $
extends continuously to
$\varphi $
extends continuously to
![]() $\partial \mathbb {D}$
and by Lemma 3.16, the trees
$\partial \mathbb {D}$
and by Lemma 3.16, the trees
![]() $\varphi ^{-1}(H)$
and
$\varphi ^{-1}(H)$
and
![]() $\varphi ^{-1}(\tilde {H})$
are homotopic rel
$\varphi ^{-1}(\tilde {H})$
are homotopic rel
![]() $\partial \mathbb {D}$
. Pushing this homotopy forward via
$\partial \mathbb {D}$
. Pushing this homotopy forward via
![]() $\varphi $
, we see that H and
$\varphi $
, we see that H and
![]() $\tilde {H}$
are homotopic rel
$\tilde {H}$
are homotopic rel
![]() $P(E_{\lambda })$
, and hence they are equivalent.
$P(E_{\lambda })$
, and hence they are equivalent.
5 Separating dynamic rays: embedding the tree into the plane
In this section, we show the existence of homotopy Hubbard trees through an explicit construction. We use the triod algorithm from the preceding section to determine the middle points of post-singular triods, and thereby the set of marked points of the homotopy Hubbard tree on the level of itineraries. Using Proposition 2.13, we pick (pre-)periodic points in the complex plane realizing the itineraries in the formal set of marked points (for pre-singular itineraries, the construction is a bit more involved because there is no actual (pre-)periodic point in the plane realizing this itinerary).
It remains to find the right way to embed the edges of the tree into the complex plane. Our main idea is to find an embedded tree which does not intersect any dynamic rays landing at a marked point. (This statement is only approximately true; some rays landing at pre-singular marked points need to be intersected, but we do so in a controlled way.)
This is partially motivated by Proposition 4.9: if there exists a homotopy Hubbard tree, then, up to homotopy rel
![]() $P(E_{\lambda })$
, every access to the tree at every post-singular point contains a dynamic ray. In particular, this ray does not intersect the homotopy Hubbard tree. Another reason is the analogy to polynomials. A polynomial Hubbard tree does not intersect any dynamic rays. If a polynomial does not have bounded Fatou components, every access to every point on its Hubbard tree contains a dynamic ray.
$P(E_{\lambda })$
, every access to the tree at every post-singular point contains a dynamic ray. In particular, this ray does not intersect the homotopy Hubbard tree. Another reason is the analogy to polynomials. A polynomial Hubbard tree does not intersect any dynamic rays. If a polynomial does not have bounded Fatou components, every access to every point on its Hubbard tree contains a dynamic ray.
The key observation is that the union of the rays landing at marked points partitions the plane in a meaningful way: there exists an embedded tree spanned by
![]() $P(E_{\lambda })$
that does not intersect these rays (except for some rays landing at pre-singular points, as noted above), and this tree is unique up to homotopy rel
$P(E_{\lambda })$
that does not intersect these rays (except for some rays landing at pre-singular points, as noted above), and this tree is unique up to homotopy rel
![]() $P(E_{\lambda })$
. As the rays landing at marked points form a forward invariant set, the pre-image tree also does not intersect them, so the embedded tree is invariant up to homotopy. Expansivity of the induced self-map follows because different marked points have different itineraries, so the embedded tree is a homotopy Hubbard tree for
$P(E_{\lambda })$
. As the rays landing at marked points form a forward invariant set, the pre-image tree also does not intersect them, so the embedded tree is invariant up to homotopy. Expansivity of the induced self-map follows because different marked points have different itineraries, so the embedded tree is a homotopy Hubbard tree for
![]() $E_{\lambda }$
.
$E_{\lambda }$
.
Let us begin with the construction of homotopy Hubbard trees. At first, we determine the set of marked points on the level of itineraries by using the triod algorithm. Throughout this section,
![]() $\nu $
denotes the kneading sequence of the exponential map
$\nu $
denotes the kneading sequence of the exponential map
![]() $E_{\lambda }$
(recall Lemma 4.1). Let
$E_{\lambda }$
(recall Lemma 4.1). Let
![]() $\Omega ^+(\star \nu ):=\{\sigma ^{\circ k}(\star \nu )~\colon ~k\geq 0\}$
denote the forward orbit of
$\Omega ^+(\star \nu ):=\{\sigma ^{\circ k}(\star \nu )~\colon ~k\geq 0\}$
denote the forward orbit of
![]() $\star \nu $
under the shift map
$\star \nu $
under the shift map
![]() $\sigma $
. This is a finite set because
$\sigma $
. This is a finite set because
![]() $\nu $
is pre-periodic. We set
$\nu $
is pre-periodic. We set
where the union runs over all formal triods consisting of sequences in
![]() $\Omega ^+(\star \nu )$
: we are adding all branch points of triods formed by post-singular points and
$\Omega ^+(\star \nu )$
: we are adding all branch points of triods formed by post-singular points and
![]() $\star \nu $
to the set of post-singular points. We call
$\star \nu $
to the set of post-singular points. We call
![]() $V_\nu $
the formal vertex set. The following properties of
$V_\nu $
the formal vertex set. The following properties of
![]() $V_\nu $
will be proved later in this section.
$V_\nu $
will be proved later in this section.
Lemma 5.1. (The formal vertex set)
The formal vertex set
![]() $V_\nu $
has the following properties.
$V_\nu $
has the following properties.
-
(1) It is forward invariant under the shift map, that is,
 $\sigma (V_\nu )\subset V_\nu $
.
$\sigma (V_\nu )\subset V_\nu $
. -
(2) It consists entirely of formal (pre-)periodic points, that is,
 $V_\nu \subset \mathcal {S}_\nu $
.
$V_\nu \subset \mathcal {S}_\nu $
. -
(3) It is closed under taking triods: for every triod
 $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
of formal vertices
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
of formal vertices
 $\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\in V_\nu $
, we have
$\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\in V_\nu $
, we have
 $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})\in V_\nu $
.
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})\in V_\nu $
.
Next, we embed the formal vertex set into the complex plane. The resulting set will become the set of marked points of the yet to be constructed homotopy Hubbard tree. First, assume that
![]() $\mathtt {\underline {t}}\in V_\nu $
is not a pre-singular point, that is, the itinerary
$\mathtt {\underline {t}}\in V_\nu $
is not a pre-singular point, that is, the itinerary
![]() $\mathtt {\underline {t}}\in \mathbb {Z}^{\mathbb {N}}$
is (pre-)periodic and
$\mathtt {\underline {t}}\in \mathbb {Z}^{\mathbb {N}}$
is (pre-)periodic and
![]() $\sigma ^{\circ n}(\mathtt {\underline {t}})\neq \nu $
for all
$\sigma ^{\circ n}(\mathtt {\underline {t}})\neq \nu $
for all
![]() $n\in \mathbb {N}$
. By Proposition 2.13, there is exactly one (pre-)periodic point
$n\in \mathbb {N}$
. By Proposition 2.13, there is exactly one (pre-)periodic point
![]() $v_{\mathtt {\underline {t}}}\in \mathbb {C}$
with
$v_{\mathtt {\underline {t}}}\in \mathbb {C}$
with
![]() $\operatorname {\mathrm {It}}(v_{\mathtt {\underline {t}}}~\vert ~\underline {s})=\mathtt {\underline {t}}$
. This is the point we assign to our formal vertex
$\operatorname {\mathrm {It}}(v_{\mathtt {\underline {t}}}~\vert ~\underline {s})=\mathtt {\underline {t}}$
. This is the point we assign to our formal vertex
![]() $\mathtt {\underline {t}}$
.
$\mathtt {\underline {t}}$
.
For a pre-singular itinerary
![]() $\mathtt {\underline {t}}\in V_\nu $
, there is no (pre-)periodic point in
$\mathtt {\underline {t}}\in V_\nu $
, there is no (pre-)periodic point in
![]() $\mathbb {C}$
of itinerary
$\mathbb {C}$
of itinerary
![]() $\mathtt {\underline {t}}$
. This issue could be addressed by adding further points at infinity corresponding to iterated pre-images of
$\mathtt {\underline {t}}$
. This issue could be addressed by adding further points at infinity corresponding to iterated pre-images of
![]() $-\infty $
to the plane. For brevity, we take a more hands-on approach: we choose surrogate points in the plane which are sufficiently close to these iterated pre-images. In our terms, this means that the itinerary of the vertex
$-\infty $
to the plane. For brevity, we take a more hands-on approach: we choose surrogate points in the plane which are sufficiently close to these iterated pre-images. In our terms, this means that the itinerary of the vertex
![]() $v_{\mathtt {\underline {t}}}\in \mathbb {C}$
shares sufficiently many entries with
$v_{\mathtt {\underline {t}}}\in \mathbb {C}$
shares sufficiently many entries with
![]() $\mathtt {\underline {t}}$
. To make this precise, let
$\mathtt {\underline {t}}$
. To make this precise, let
and pick a closed neighborhood U of the singular value
![]() $0$
with the following properties.
$0$
with the following properties.
-
(1)
 $E_{\lambda }^{-n}(U)\cap E_{\lambda }^{-m}(U)=\emptyset $
for all distinct
$E_{\lambda }^{-n}(U)\cap E_{\lambda }^{-m}(U)=\emptyset $
for all distinct
 $n,m\in \{0,\ldots , N+1\}.$
$n,m\in \{0,\ldots , N+1\}.$
-
(2) For every
 $n\in \{1,\ldots , N+1\}$
, the pre-image
$n\in \{1,\ldots , N+1\}$
, the pre-image
 $E_{\lambda }^{-n}(U)$
does not intersect the union of the set of non-pre-singular vertices and the dynamic rays landing at these points.
$E_{\lambda }^{-n}(U)$
does not intersect the union of the set of non-pre-singular vertices and the dynamic rays landing at these points. -
(3) U is bounded by a Jordan curve such that the dynamic ray
 $g_{\underline {s}}$
landing at the singular value intersects the boundary of U exactly once, that is, there is a unique potential
$g_{\underline {s}}$
landing at the singular value intersects the boundary of U exactly once, that is, there is a unique potential
 $t_0$
such that
$t_0$
such that
 $g_{\underline {s}}(t_0)\in \partial U$
, whereas
$g_{\underline {s}}(t_0)\in \partial U$
, whereas
 $g_{\underline {s}}(t)\in U$
for
$g_{\underline {s}}(t)\in U$
for
 $t<t_0$
and
$t<t_0$
and
 $g_{\underline {s}}(t)\in \mathbb {C}\setminus \overline {U}$
for
$g_{\underline {s}}(t)\in \mathbb {C}\setminus \overline {U}$
for
 $t>t_0$
. This is only to simplify topological considerations involving U.
$t>t_0$
. This is only to simplify topological considerations involving U.
The first condition is equivalent to
![]() $U\cap E_{\lambda }^{\circ n}(U)=\emptyset $
for all
$U\cap E_{\lambda }^{\circ n}(U)=\emptyset $
for all
![]() $n\in \{1,\ldots , N+1\}$
and this is obviously fulfilled for U small enough because
$n\in \{1,\ldots , N+1\}$
and this is obviously fulfilled for U small enough because
![]() $0$
is not periodic. The second condition is equivalent to U not intersecting the union of the set of non-pre-singular vertices and the dynamic rays landing at those except for the singular value
$0$
is not periodic. The second condition is equivalent to U not intersecting the union of the set of non-pre-singular vertices and the dynamic rays landing at those except for the singular value
![]() $0$
. Again, this is true for U small enough. Finally, condition (3) can always be ensured by shrinking a neighborhood that fulfills conditions (1) and (2).
$0$
. Again, this is true for U small enough. Finally, condition (3) can always be ensured by shrinking a neighborhood that fulfills conditions (1) and (2).
Let
![]() $\log _{\underline {s},k}\colon \mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {s}})\cup \{0\})\to D_k$
be the branch of the inverse of
$\log _{\underline {s},k}\colon \mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {s}})\cup \{0\})\to D_k$
be the branch of the inverse of
![]() $E_{\lambda }$
with the stated domain and co-domain. For every itinerary
$E_{\lambda }$
with the stated domain and co-domain. For every itinerary
![]() $\mathtt {\underline {t}}\in \mathcal {S}_\nu $
of the form
$\mathtt {\underline {t}}\in \mathcal {S}_\nu $
of the form
![]() $\mathtt {\underline {t}}=k_1\ldots k_n\star \nu $
with
$\mathtt {\underline {t}}=k_1\ldots k_n\star \nu $
with
![]() $n\in \{0,\ldots , N\}$
, we define
$n\in \{0,\ldots , N\}$
, we define
that is,
![]() $U_{\mathtt {\underline {t}}}$
is the iterated pre-image under
$U_{\mathtt {\underline {t}}}$
is the iterated pre-image under
![]() $E_{\lambda }$
of the domain U constructed above by the branches of the logarithm prescribed by the entries of
$E_{\lambda }$
of the domain U constructed above by the branches of the logarithm prescribed by the entries of
![]() $\mathtt {\underline {t}}$
. Note that by property (1) of U, distinct
$\mathtt {\underline {t}}$
. Note that by property (1) of U, distinct
![]() $U_{\mathtt {\underline {t}}}$
and
$U_{\mathtt {\underline {t}}}$
and
![]() $U_{\mathtt {\underline {u}}}$
are disjoint. We assign to
$U_{\mathtt {\underline {u}}}$
are disjoint. We assign to
![]() $\star \nu \in V_\nu $
an arbitrary point
$\star \nu \in V_\nu $
an arbitrary point
![]() $v_{\star \nu }\in U_{\star \nu }$
which will later become the singular point (see the paragraph after Definition 3.7) of the homotopy Hubbard tree. If
$v_{\star \nu }\in U_{\star \nu }$
which will later become the singular point (see the paragraph after Definition 3.7) of the homotopy Hubbard tree. If
![]() $\mathtt {\underline {t}}=k_1\ldots k_n\star \nu $
is pre-singular, we associate to
$\mathtt {\underline {t}}=k_1\ldots k_n\star \nu $
is pre-singular, we associate to
![]() $\mathtt {\underline {t}}$
the point
$\mathtt {\underline {t}}$
the point
To every formal vertex
![]() $\mathtt {\underline {t}}\in V_\nu $
, we have thus associated a point
$\mathtt {\underline {t}}\in V_\nu $
, we have thus associated a point
![]() $v_{\mathtt {\underline {t}}}\in \mathbb {C}$
.
$v_{\mathtt {\underline {t}}}\in \mathbb {C}$
.
Definition 5.2. (Vertex set and triods of vertices)
We define the vertex set
![]() $V\subset \mathbb {C}$
to be the set of all
$V\subset \mathbb {C}$
to be the set of all
![]() $v_{\mathtt {\underline {t}}}$
for
$v_{\mathtt {\underline {t}}}$
for
![]() $\mathtt {\underline {t}}\in V_\nu $
. A triod of vertices
$\mathtt {\underline {t}}\in V_\nu $
. A triod of vertices
![]() $[v_{\mathtt {\underline {t}}}, v_{\mathtt {\underline {u}}}, v_{\mathtt {\underline {v}}}]$
is a triple of distinct vertices
$[v_{\mathtt {\underline {t}}}, v_{\mathtt {\underline {u}}}, v_{\mathtt {\underline {v}}}]$
is a triple of distinct vertices
![]() $v_{\mathtt {\underline {t}}}, v_{\mathtt {\underline {u}}}, v_{\mathtt {\underline {v}}}\in V$
.
$v_{\mathtt {\underline {t}}}, v_{\mathtt {\underline {u}}}, v_{\mathtt {\underline {v}}}\in V$
.
As triods of vertices are in natural bijection to triods of formal vertices, we use the terminology introduced for formal triods for vertex triods too. In particular, we call a triod of vertices (pre-singularly) branched or (pre-singularly) linear if the corresponding formal triod is of this type.
We now turn our attention to constructing the edges of a homotopy Hubbard tree. The partitioning property mentioned at the beginning of this section rests on a result about dynamic rays separating the vertex set V: if
![]() $p, q, r\in V$
are distinct vertices and the corresponding formal triod
$p, q, r\in V$
are distinct vertices and the corresponding formal triod
![]() $[p, q, r]$
is branched, then there exist (pre-)periodic dynamic rays
$[p, q, r]$
is branched, then there exist (pre-)periodic dynamic rays
![]() $g_1,g_2,g_3$
of itinerary
$g_1,g_2,g_3$
of itinerary
![]() $\mathtt {\underline {b}}[p, q, r]$
, such that p, q, and r are separated by the rays
$\mathtt {\underline {b}}[p, q, r]$
, such that p, q, and r are separated by the rays
![]() $g_i$
, that is, such that these three points are contained in different connected components of
$g_i$
, that is, such that these three points are contained in different connected components of
![]() $\mathbb {C}\setminus \bigcup \operatorname {\mathrm {Tr}}(g_i)$
. If
$\mathbb {C}\setminus \bigcup \operatorname {\mathrm {Tr}}(g_i)$
. If
![]() $[p,q,r]$
is linear, there are two (pre-)periodic rays landing at the middle point and separating the other two points from each other. To prove the existence of such separating dynamic rays, we use the language of external addresses. This requires a variant of the triod algorithm operating on the level of external addresses.
$[p,q,r]$
is linear, there are two (pre-)periodic rays landing at the middle point and separating the other two points from each other. To prove the existence of such separating dynamic rays, we use the language of external addresses. This requires a variant of the triod algorithm operating on the level of external addresses.
Definition 5.3. (Formal triods and the formal triod map)
Recall our notation
![]() $\mathcal {I}=\{I_k\}_{k\in \mathbb {Z}}$
for the dynamical partition of the shift space
$\mathcal {I}=\{I_k\}_{k\in \mathbb {Z}}$
for the dynamical partition of the shift space
![]() $\mathcal {S}$
with respect to
$\mathcal {S}$
with respect to
![]() $\underline {s}$
(see §2). In particular,
$\underline {s}$
(see §2). In particular,
![]() $\underline {s}$
is the external address of a dynamic ray
$\underline {s}$
is the external address of a dynamic ray
![]() $g_{\underline {s}}$
landing at the singular value
$g_{\underline {s}}$
landing at the singular value
![]() $0$
.
$0$
.
A formal triod of external addresses is a triple
![]() $[\underline {t}, \underline {u}, \underline {v}]$
of external addresses
$[\underline {t}, \underline {u}, \underline {v}]$
of external addresses
![]() $\underline {t},\underline {u}, \underline {v}\in \mathcal {S}$
such that
$\underline {t},\underline {u}, \underline {v}\in \mathcal {S}$
such that
![]() $\underline {t}\prec \underline {u}\prec \underline {v}$
, and
$\underline {t}\prec \underline {u}\prec \underline {v}$
, and
![]() $\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s}),\operatorname {\mathrm {It}}(\underline {u}~\vert ~\underline {s}),\operatorname {\mathrm {It}}(\underline {v}~\vert ~\underline {s})\in \mathcal {S}_\nu $
are distinct itineraries. We define the formal triod map
$\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s}),\operatorname {\mathrm {It}}(\underline {u}~\vert ~\underline {s}),\operatorname {\mathrm {It}}(\underline {v}~\vert ~\underline {s})\in \mathcal {S}_\nu $
are distinct itineraries. We define the formal triod map
![]() $\mathcal {T}_{\mathcal {S}}$
on the level of external addresses as follows:
$\mathcal {T}_{\mathcal {S}}$
on the level of external addresses as follows:
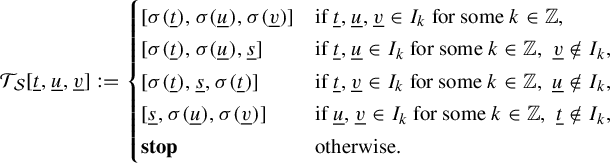 $$ \begin{align*} \mathcal{T}_{\mathcal{S}}[\underline{t}, \underline{u}, \underline{v}]:= \begin{cases} [\sigma(\underline{t}), \sigma(\underline{u}), \sigma(\underline{v})]&\text{if}~\underline{t},\underline{u},\underline{v}\in I_k~\text{for some}~k\in\mathbb{Z},\\ [\sigma(\underline{t}), \sigma(\underline{u}), \underline{s}]&\text{if}~\underline{t},\underline{u}\in I_k~\text{for some}~k\in\mathbb{Z},~\underline{v}\notin I_k,\\ [\sigma(\underline{t}), \underline{s}, \sigma(\underline{t})]&\text{if}~\underline{t},\underline{v}\in I_k~\text{for some}~k\in\mathbb{Z},~\underline{u}\notin I_k,\\ [\underline{s}, \sigma(\underline{u}), \sigma(\underline{v})]&\text{if}~\underline{u},\underline{v}\in I_k~\text{for some}~k\in\mathbb{Z},~\underline{t}\notin I_k,\\ \textbf{stop}&\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{T}_{\mathcal{S}}[\underline{t}, \underline{u}, \underline{v}]:= \begin{cases} [\sigma(\underline{t}), \sigma(\underline{u}), \sigma(\underline{v})]&\text{if}~\underline{t},\underline{u},\underline{v}\in I_k~\text{for some}~k\in\mathbb{Z},\\ [\sigma(\underline{t}), \sigma(\underline{u}), \underline{s}]&\text{if}~\underline{t},\underline{u}\in I_k~\text{for some}~k\in\mathbb{Z},~\underline{v}\notin I_k,\\ [\sigma(\underline{t}), \underline{s}, \sigma(\underline{t})]&\text{if}~\underline{t},\underline{v}\in I_k~\text{for some}~k\in\mathbb{Z},~\underline{u}\notin I_k,\\ [\underline{s}, \sigma(\underline{u}), \sigma(\underline{v})]&\text{if}~\underline{u},\underline{v}\in I_k~\text{for some}~k\in\mathbb{Z},~\underline{t}\notin I_k,\\ \textbf{stop}&\text{otherwise}. \end{cases} \end{align*} $$
We claim that if the stop case is not reached, the image is again a formal triod. The following result will help us to show this fact.
Lemma 5.4. (Order-preserving restrictions)
Let
![]() $I=(k\underline {s},(k+1)\underline {s})$
be a partition sector and let
$I=(k\underline {s},(k+1)\underline {s})$
be a partition sector and let
![]() $I^-:=(k\underline {s},(k+1)\underline {s}]$
. The restriction
$I^-:=(k\underline {s},(k+1)\underline {s}]$
. The restriction
is a bijection and preserves the cyclic order.
Proof The shift map
![]() $\sigma $
is strictly monotonically increasing with respect to the linear order on
$\sigma $
is strictly monotonically increasing with respect to the linear order on
![]() $\mathcal {S}$
on both of the sets
$\mathcal {S}$
on both of the sets
![]() $I_l:=\{\underline {t}\in I\colon \underline {t}=k\ldots \}$
and
$I_l:=\{\underline {t}\in I\colon \underline {t}=k\ldots \}$
and
![]() $I_u:=\{\underline {t}\in I\colon \underline {t}=(k+1)\ldots \}\cup \{(k+1)\underline {s}\}$
. It maps
$I_u:=\{\underline {t}\in I\colon \underline {t}=(k+1)\ldots \}\cup \{(k+1)\underline {s}\}$
. It maps
![]() $I_l$
bijectively onto
$I_l$
bijectively onto
![]() $\{\underline {t}\in \mathcal {S}\colon \underline {t}>\underline {s}\}$
and
$\{\underline {t}\in \mathcal {S}\colon \underline {t}>\underline {s}\}$
and
![]() $I_u$
bijectively onto
$I_u$
bijectively onto
![]() $\{\underline {t}\in \mathcal {S}\colon \underline {t}\leq \underline {s}\}$
. In particular, it swaps the two sets globally, that is,
$\{\underline {t}\in \mathcal {S}\colon \underline {t}\leq \underline {s}\}$
. In particular, it swaps the two sets globally, that is,
![]() $\sigma (\underline {t})>\sigma (\underline {u})~\text {for all}~\underline {t}\in I_l~\text {and all}~\underline {u}\in I_u$
. See Figure 2 for a sketch of the mapping behavior of
$\sigma (\underline {t})>\sigma (\underline {u})~\text {for all}~\underline {t}\in I_l~\text {and all}~\underline {u}\in I_u$
. See Figure 2 for a sketch of the mapping behavior of
![]() $\sigma $
. It follows that
$\sigma $
. It follows that
![]() $\sigma |_{I^-}$
is a bijection. One can see that
$\sigma |_{I^-}$
is a bijection. One can see that
![]() $\sigma |_{I^-}$
preserves the cyclic order by checking all possible configurations of the three external addresses with respect to
$\sigma |_{I^-}$
preserves the cyclic order by checking all possible configurations of the three external addresses with respect to
![]() $I_l$
and
$I_l$
and
![]() $I_u$
. See Figure 2 for a configuration under which the cyclic order, but not the linear order, of the addresses
$I_u$
. See Figure 2 for a configuration under which the cyclic order, but not the linear order, of the addresses
![]() $\underline {t}$
,
$\underline {t}$
,
![]() $\underline {u}$
, and
$\underline {u}$
, and
![]() $\underline {v}$
is preserved.
$\underline {v}$
is preserved.
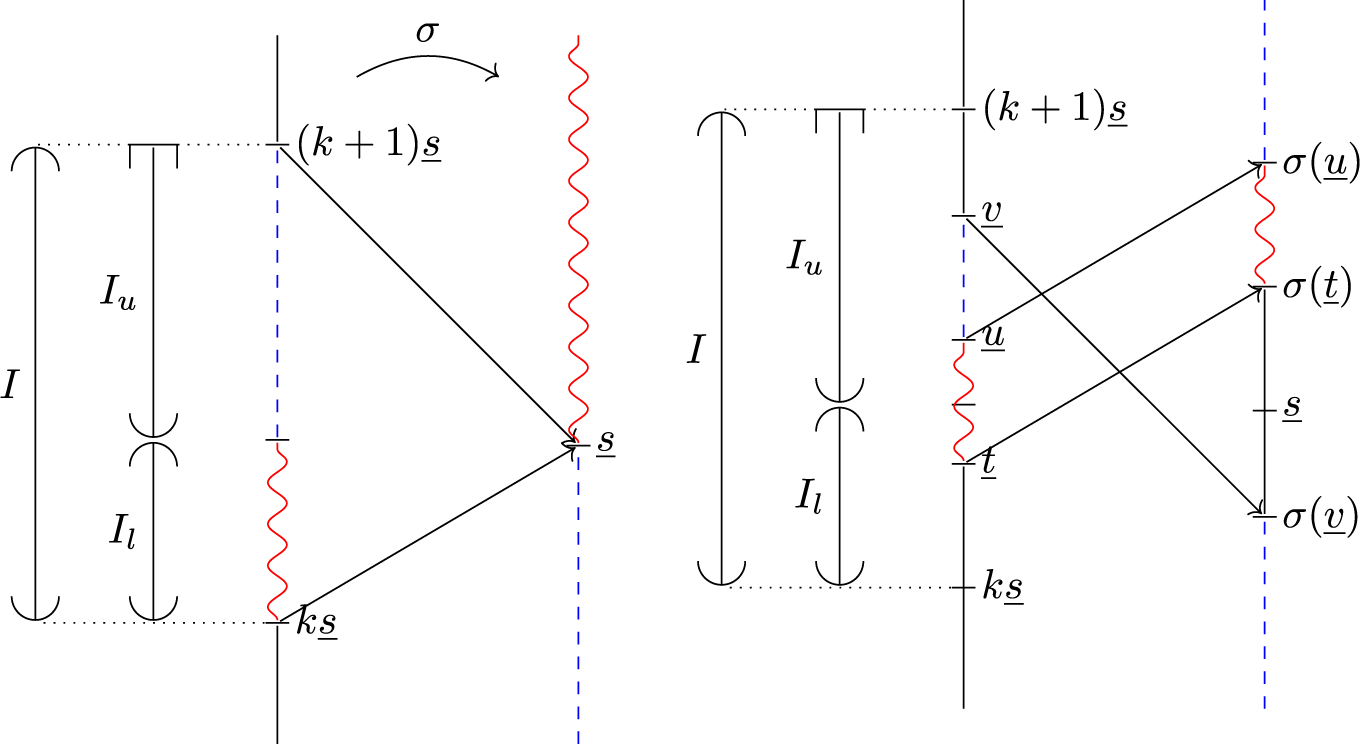
Figure 2 Sketch illustrating the mapping behavior of the shift map. The left sketch shows how the intervals
![]() $I_l$
and
$I_l$
and
![]() $I_u$
are exchanged globally, while the restriction of the shift to each of them is strictly monotonically increasing. The right figure shows that the linear order of the image addresses might change, but the cyclic order stays the same. It also illustrates that an interval splits if it contains the address
$I_u$
are exchanged globally, while the restriction of the shift to each of them is strictly monotonically increasing. The right figure shows that the linear order of the image addresses might change, but the cyclic order stays the same. It also illustrates that an interval splits if it contains the address
![]() $ \underline {s}$
.
$ \underline {s}$
.
Let us write
![]() $[\underline {\tilde {t}},\underline {\tilde {u}},\underline {\tilde {v}}]:=\mathcal {T}_{\mathcal {S}}[\underline {t}, \underline {u}, \underline {v}]$
. Lemma 5.4 shows that
$[\underline {\tilde {t}},\underline {\tilde {u}},\underline {\tilde {v}}]:=\mathcal {T}_{\mathcal {S}}[\underline {t}, \underline {u}, \underline {v}]$
. Lemma 5.4 shows that
![]() $\underline {\tilde {t}}\prec \underline {\tilde {u}}\prec \underline {\tilde {v}}$
. It remains to show that
$\underline {\tilde {t}}\prec \underline {\tilde {u}}\prec \underline {\tilde {v}}$
. It remains to show that
![]() $\tilde {\underline {\mathtt {x}}}:=\operatorname {\mathrm {It}}(\underline {\tilde {x}}~\vert ~\underline {s})$
are distinct for
$\tilde {\underline {\mathtt {x}}}:=\operatorname {\mathrm {It}}(\underline {\tilde {x}}~\vert ~\underline {s})$
are distinct for
![]() $x\in \{t,u,v\}$
. The map
$x\in \{t,u,v\}$
. The map
![]() $[\underline {t},\underline {u},\underline {v}]\mapsto [\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
(where
$[\underline {t},\underline {u},\underline {v}]\mapsto [\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
(where
![]() $\mathtt {\underline {x}}:=\operatorname {\mathrm {It}}(\underline {{x}}~\vert ~\underline {s})$
as before) is a semi-conjugation between
$\mathtt {\underline {x}}:=\operatorname {\mathrm {It}}(\underline {{x}}~\vert ~\underline {s})$
as before) is a semi-conjugation between
![]() $\mathcal {T}_{\mathcal {S}}$
and
$\mathcal {T}_{\mathcal {S}}$
and
![]() $\mathcal {T}$
. The sequences
$\mathcal {T}$
. The sequences
![]() $\tilde {\underline {\mathtt {x}}}$
are distinct because
$\tilde {\underline {\mathtt {x}}}$
are distinct because
![]() $[\underline {\tilde { \mathtt{t}}},\tilde {\underline {\mathtt {u}}},\tilde {\underline {\mathtt {v}}}]=\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
, and triods of formal (pre-)periodic points are mapped to triods of formal (pre-)periodic points under iteration of
$[\underline {\tilde { \mathtt{t}}},\tilde {\underline {\mathtt {u}}},\tilde {\underline {\mathtt {v}}}]=\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
, and triods of formal (pre-)periodic points are mapped to triods of formal (pre-)periodic points under iteration of
![]() $\mathcal {T}$
by the considerations after Definition 4.12. We call the triods
$\mathcal {T}$
by the considerations after Definition 4.12. We call the triods
![]() $[\underline {t}, \underline {u}, \underline {v}]$
and
$[\underline {t}, \underline {u}, \underline {v}]$
and
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
associated to each other. We define the middle point
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
associated to each other. We define the middle point
![]() $\mathtt {\underline {b}}[\underline {t},\underline {u},\underline {v}]$
to be the middle point of
$\mathtt {\underline {b}}[\underline {t},\underline {u},\underline {v}]$
to be the middle point of
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
, and the majority vote
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
, and the majority vote
![]() $\mathtt {\underline {m}}[\underline {t}, \underline {u}, \underline {v}]$
to be the majority vote of
$\mathtt {\underline {m}}[\underline {t}, \underline {u}, \underline {v}]$
to be the majority vote of
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
. We call
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
. We call
![]() $[\underline {v},\underline {t},\underline {u}]$
branched if
$[\underline {v},\underline {t},\underline {u}]$
branched if
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is branched, and linear otherwise. If
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is branched, and linear otherwise. If
![]() $\mathcal {T}^{{\kern1.5pt}\circ i_0}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]=\textbf {stop}$
, then
$\mathcal {T}^{{\kern1.5pt}\circ i_0}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]=\textbf {stop}$
, then
![]() $[\underline {t}, \underline {u}, \underline {v}]$
reaches the stop case at the same iteration step and vice versa. We have seen in §4 that if
$[\underline {t}, \underline {u}, \underline {v}]$
reaches the stop case at the same iteration step and vice versa. We have seen in §4 that if
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
can be iterated indefinitely, all of the three sequences will eventually be contained in
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
can be iterated indefinitely, all of the three sequences will eventually be contained in
![]() $\mathcal {S}_\nu \setminus \Omega ^-(\star \nu )$
, and
$\mathcal {S}_\nu \setminus \Omega ^-(\star \nu )$
, and
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is (pre-)periodic under iteration of
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is (pre-)periodic under iteration of
![]() $\mathcal {T}$
. By Theorem 2.10 and Proposition 2.13, there are only finitely many external addresses associated to a formal (pre-)periodic point
$\mathcal {T}$
. By Theorem 2.10 and Proposition 2.13, there are only finitely many external addresses associated to a formal (pre-)periodic point
![]() $\mathtt {\underline {t}}\in \mathcal {S}_\nu \setminus \Omega ^-(\star \nu )$
. Therefore,
$\mathtt {\underline {t}}\in \mathcal {S}_\nu \setminus \Omega ^-(\star \nu )$
. Therefore,
![]() $[\underline {t}, \underline {u}, \underline {v}]$
is eventually periodic under iteration of
$[\underline {t}, \underline {u}, \underline {v}]$
is eventually periodic under iteration of
![]() $\mathcal {T}_{\mathcal {S}}$
.
$\mathcal {T}_{\mathcal {S}}$
.
For the proof of the existence of separating rays, which works on the combinatorial level, the following results will be useful.
Lemma 5.5. (Pullbacks of intervals)
Let
![]() $[\underline {t}^1, \underline {t}^2, \underline {t}^3]$
be a formal triod of external addresses which can be iterated at least once before reaching the stop case, let
$[\underline {t}^1, \underline {t}^2, \underline {t}^3]$
be a formal triod of external addresses which can be iterated at least once before reaching the stop case, let
![]() $[\underline {u}^1, \underline {u}^2, \underline {u}^3]:=\mathcal {T}_{\mathcal {S}}[\underline {t}^1, \underline {t}^2, \underline {t}^3]$
be its image triod, and let
$[\underline {u}^1, \underline {u}^2, \underline {u}^3]:=\mathcal {T}_{\mathcal {S}}[\underline {t}^1, \underline {t}^2, \underline {t}^3]$
be its image triod, and let
![]() $k:=\mathtt {m}(\underline {t}^1, \underline {t}^2, \underline {t}^3)$
be its majority vote. Write
$k:=\mathtt {m}(\underline {t}^1, \underline {t}^2, \underline {t}^3)$
be its majority vote. Write
![]() $J_n:=(\underline {t}^n,\underline {t}^{n+1})$
and
$J_n:=(\underline {t}^n,\underline {t}^{n+1})$
and
![]() $J_n':=(\underline {u}^n, \underline {u}^{n+1})$
for
$J_n':=(\underline {u}^n, \underline {u}^{n+1})$
for
![]() $n\in \{1,2,3\}$
(with indices labeled mod 3) for the intervals of the partition of the shift space by the initial triod and the image triod, respectively. Then we have
$n\in \{1,2,3\}$
(with indices labeled mod 3) for the intervals of the partition of the shift space by the initial triod and the image triod, respectively. Then we have
Proof Because not all
![]() $\underline {t}^i$
are contained in distinct partition sectors by hypothesis, we have
$\underline {t}^i$
are contained in distinct partition sectors by hypothesis, we have
![]() $\underline {t}^j\notin I_k$
for at most one j. We define a triod
$\underline {t}^j\notin I_k$
for at most one j. We define a triod
![]() $[\underline {\tilde {t}}^1, \underline {\tilde {t}}^2, \underline {\tilde {t}}^3]$
by replacing such a
$[\underline {\tilde {t}}^1, \underline {\tilde {t}}^2, \underline {\tilde {t}}^3]$
by replacing such a
![]() $\underline {t}^j$
(if any) by the unique pre-image of
$\underline {t}^j$
(if any) by the unique pre-image of
![]() $\underline {s}$
in
$\underline {s}$
in
![]() $I_k^-$
. Then
$I_k^-$
. Then
![]() $\mathcal {T}_{\mathcal {S}}[\underline {t}^1, \underline {t}^2, \underline {t}^3]=\mathcal {T}_{\mathcal {S}}[\underline {\tilde {t}}^1, \underline {\tilde {t}}^2, \underline {\tilde {t}}^3]=[\sigma (\underline {\tilde {t}}^1), \sigma (\underline {\tilde {t}}^2), \sigma (\underline {\tilde {t}}^3)]$
. Furthermore, we have
$\mathcal {T}_{\mathcal {S}}[\underline {t}^1, \underline {t}^2, \underline {t}^3]=\mathcal {T}_{\mathcal {S}}[\underline {\tilde {t}}^1, \underline {\tilde {t}}^2, \underline {\tilde {t}}^3]=[\sigma (\underline {\tilde {t}}^1), \sigma (\underline {\tilde {t}}^2), \sigma (\underline {\tilde {t}}^3)]$
. Furthermore, we have
![]() $\tilde {J}_n\cap I_k= J_n\cap I_k$
, where
$\tilde {J}_n\cap I_k= J_n\cap I_k$
, where
![]() $\tilde {J}_n:=(\underline {\tilde {t}}^n,\underline {\tilde {t}}^{n+1})$
. Let
$\tilde {J}_n:=(\underline {\tilde {t}}^n,\underline {\tilde {t}}^{n+1})$
. Let
![]() $\underline {v}\in \sigma ^{-1}(J_n')\cap I_k$
be an external address. We have
$\underline {v}\in \sigma ^{-1}(J_n')\cap I_k$
be an external address. We have
![]() $\sigma (\underline {v})\in J_n'$
, that is,
$\sigma (\underline {v})\in J_n'$
, that is,
![]() $\sigma (\underline {\tilde {t}}^n)\prec \sigma (\underline {v})\prec \sigma (\underline {\tilde {t}}^{n+1})$
. It follows from Lemma 5.4 that
$\sigma (\underline {\tilde {t}}^n)\prec \sigma (\underline {v})\prec \sigma (\underline {\tilde {t}}^{n+1})$
. It follows from Lemma 5.4 that
![]() $\underline {\tilde {t}}^n\prec \underline {v}\prec \underline {\tilde {t}}^{n+1}$
and, therefore,
$\underline {\tilde {t}}^n\prec \underline {v}\prec \underline {\tilde {t}}^{n+1}$
and, therefore,
![]() $\underline {v}\in \tilde {J}_n\cap I_k\subset J_n$
.
$\underline {v}\in \tilde {J}_n\cap I_k\subset J_n$
.
Lemma 5.6. (Splitting of intervals)
Let
![]() $I,I'\in \mathcal {I}$
be partition sectors and let
$I,I'\in \mathcal {I}$
be partition sectors and let
![]() $J\subset I$
be an interval. If
$J\subset I$
be an interval. If
![]() $\underline {s}\notin J$
, then
$\underline {s}\notin J$
, then
![]() $J':=\sigma ^{-1}(J)\cap I'$
is an interval and it is of the form
$J':=\sigma ^{-1}(J)\cap I'$
is an interval and it is of the form
![]() $J'=\{k\underline {t}\colon \underline {t}\in J\}$
for some
$J'=\{k\underline {t}\colon \underline {t}\in J\}$
for some
![]() $k\in \mathbb {Z}$
.
$k\in \mathbb {Z}$
.
Proof We have
![]() $I'=(k\underline {s},(k+1)\underline {s})$
for some
$I'=(k\underline {s},(k+1)\underline {s})$
for some
![]() $k\in \mathbb {Z}$
. As J is entirely contained in some partition sector and
$k\in \mathbb {Z}$
. As J is entirely contained in some partition sector and
![]() $\underline {s}\notin J$
, we either have
$\underline {s}\notin J$
, we either have
![]() $\underline {t}>\underline {s}$
for all
$\underline {t}>\underline {s}$
for all
![]() $\underline {t}\in J$
or
$\underline {t}\in J$
or
![]() $\underline {t}<\underline {s}$
for all
$\underline {t}<\underline {s}$
for all
![]() $\underline {t}\in J$
. Assume that the first case is true (the second case works analogously). Then we have
$\underline {t}\in J$
. Assume that the first case is true (the second case works analogously). Then we have
![]() $k\underline {t}\in I'$
for all
$k\underline {t}\in I'$
for all
![]() $\underline {t}\in J$
. As
$\underline {t}\in J$
. As
![]() $\sigma |_{I'}$
is injective, we have
$\sigma |_{I'}$
is injective, we have
![]() $J'=\{k\underline {t}\colon \underline {t}\in J\}$
. The right part of Figure 2 illustrates why an interval containing
$J'=\{k\underline {t}\colon \underline {t}\in J\}$
. The right part of Figure 2 illustrates why an interval containing
![]() $\underline {s}$
splits.
$\underline {s}$
splits.
Lemma 5.7. (Unlinked addresses)
Let
![]() $\mathtt {\underline {t}},\mathtt {\underline {u}}\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
be distinct (pre-)periodic itineraries, let
$\mathtt {\underline {t}},\mathtt {\underline {u}}\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
be distinct (pre-)periodic itineraries, let
![]() $T:=(\underline {t}^i)_{i\in I}$
be the set of external addresses with
$T:=(\underline {t}^i)_{i\in I}$
be the set of external addresses with
![]() $\operatorname {\mathrm {It}}(\underline {t}^i~\vert ~\underline {s})=\mathtt {\underline {t}}$
, and let
$\operatorname {\mathrm {It}}(\underline {t}^i~\vert ~\underline {s})=\mathtt {\underline {t}}$
, and let
![]() $U:=(\underline {u}^j)_{j\in J}$
be the set of external addresses with
$U:=(\underline {u}^j)_{j\in J}$
be the set of external addresses with
![]() $\operatorname {\mathrm {It}}(\underline {u}^j~\vert ~\underline {s})=\mathtt {\underline {u}}$
. Then T and U are unlinked in the sense that there are no addresses
$\operatorname {\mathrm {It}}(\underline {u}^j~\vert ~\underline {s})=\mathtt {\underline {u}}$
. Then T and U are unlinked in the sense that there are no addresses
![]() $\underline {t},\underline {t}'\in T$
and
$\underline {t},\underline {t}'\in T$
and
![]() $\underline {u},\underline {u}'\in U$
such that
$\underline {u},\underline {u}'\in U$
such that
![]() $\underline {t}\prec \underline {u}\prec \underline {t}'\prec \underline {u}'$
.
$\underline {t}\prec \underline {u}\prec \underline {t}'\prec \underline {u}'$
.
Proof Assume to the contrary that there exist four external addresses as above. First consider the case that
![]() $\mathtt {t}_1=\star $
. Then
$\mathtt {t}_1=\star $
. Then
![]() $\underline {t}$
and
$\underline {t}$
and
![]() $\underline {t'}$
are contained in the boundary
$\underline {t'}$
are contained in the boundary
![]() $\partial \mathcal {I}$
of the dynamical partition, so
$\partial \mathcal {I}$
of the dynamical partition, so
![]() $\underline {u}$
and
$\underline {u}$
and
![]() $\underline {u}'$
are contained in different partition sectors, which contradicts the fact that they have the same itinerary. Hence, we can assume
$\underline {u}'$
are contained in different partition sectors, which contradicts the fact that they have the same itinerary. Hence, we can assume
![]() $\mathtt {t}_1,\mathtt {u}_1\neq \star $
. However then,
$\mathtt {t}_1,\mathtt {u}_1\neq \star $
. However then,
![]() $\underline {t}\prec \underline {u}\prec \underline {t}'\prec \underline {u}'$
implies
$\underline {t}\prec \underline {u}\prec \underline {t}'\prec \underline {u}'$
implies
![]() $\mathtt {t}_1=\mathtt {u}_1$
. As
$\mathtt {t}_1=\mathtt {u}_1$
. As
![]() $\sigma |_{I_{\mathtt {t}_1}}$
preserves the cyclic order, we have
$\sigma |_{I_{\mathtt {t}_1}}$
preserves the cyclic order, we have
![]() $\sigma (\underline {t})\prec \sigma (\underline {u})\prec \sigma (\underline {t}')\prec \sigma (\underline {u}')$
. Repeating this argument inductively, we obtain
$\sigma (\underline {t})\prec \sigma (\underline {u})\prec \sigma (\underline {t}')\prec \sigma (\underline {u}')$
. Repeating this argument inductively, we obtain
![]() $\mathtt {\underline {u}}=\mathtt {\underline {t}}$
, which contradicts our assumptions.
$\mathtt {\underline {u}}=\mathtt {\underline {t}}$
, which contradicts our assumptions.
Let us now prove the main combinatorial lemma of this section. Major ideas for the proof are taken from [Reference Schleicher and ZimmerSZ2, Lemma 5.2].
Lemma 5.8. (Combinatorial version of separating dynamic rays)
Let
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
be a triod of external addresses and let
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
be a triod of external addresses and let
![]() $\mathtt {\underline {b}}\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
be (pre-)periodic.
$\mathtt {\underline {b}}\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
be (pre-)periodic.
The triod
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched with
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched with
![]() $\mathtt {\underline {b}}=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
if and only if there are three distinct (pre-)periodic external addresses
$\mathtt {\underline {b}}=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
if and only if there are three distinct (pre-)periodic external addresses
![]() $\underline {s}^1, \underline {s}^2, \underline {s}^3\in \mathcal {S}$
such that
$\underline {s}^1, \underline {s}^2, \underline {s}^3\in \mathcal {S}$
such that
![]() $\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
and
$\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
and
![]() $\underline {s}^i\in (\underline {t}^i,\underline {t}^{i+1})$
(where again indices are labeled modulo 3).
$\underline {s}^i\in (\underline {t}^i,\underline {t}^{i+1})$
(where again indices are labeled modulo 3).
The triod
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is linear with
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is linear with
![]() $\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=\operatorname {\mathrm {It}}(\underline {t}^j~\vert ~\underline {s})=:\mathtt {\underline {b}}$
if and only if there are two distinct (pre-)periodic external addresses
$\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=\operatorname {\mathrm {It}}(\underline {t}^j~\vert ~\underline {s})=:\mathtt {\underline {b}}$
if and only if there are two distinct (pre-)periodic external addresses
![]() $\underline {s}^j, \underline {s}^{j+1}\in \mathcal {S}$
with
$\underline {s}^j, \underline {s}^{j+1}\in \mathcal {S}$
with
![]() $\underline {s}^j=\underline {t}^j$
and
$\underline {s}^j=\underline {t}^j$
and
![]() $\underline {s}^{j+1}\in (\underline {t}^{j+1},\underline {t}^{j+2})$
, such that
$\underline {s}^{j+1}\in (\underline {t}^{j+1},\underline {t}^{j+2})$
, such that
![]() $\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
holds.
$\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
holds.
Proof We start by proving the ‘only if’ direction.
Claim 1. If
![]() $\mathcal {T}_{\mathcal {S}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
and the result is true for
$\mathcal {T}_{\mathcal {S}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
and the result is true for
![]() $[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
, then it also holds for
$[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
, then it also holds for
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
.
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
.
Proof Assume first that
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
and, hence also,
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
and, hence also,
![]() $[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
is branched, and let
$[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
is branched, and let
![]() $\underline {\tilde {s}}^j$
be separating addresses for the image triod. Then, setting
$\underline {\tilde {s}}^j$
be separating addresses for the image triod. Then, setting
![]() $k:=\mathtt {m}(\underline {t}^1, \underline {t}^2, \underline {t}^3)$
and
$k:=\mathtt {m}(\underline {t}^1, \underline {t}^2, \underline {t}^3)$
and
![]() $\underline {s}^j:=\sigma |_{I_k}^{-1}(\underline {\tilde {s}}^j)$
, we have
$\underline {s}^j:=\sigma |_{I_k}^{-1}(\underline {\tilde {s}}^j)$
, we have
![]() $\underline {s}^j\in (\underline {t}^j,\underline {t}^{j+1})$
by Lemma 5.5. Furthermore, we have
$\underline {s}^j\in (\underline {t}^j,\underline {t}^{j+1})$
by Lemma 5.5. Furthermore, we have
![]() $\operatorname {\mathrm {It}}(\underline {s}^j~\vert ~\underline {s})=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
, so the addresses
$\operatorname {\mathrm {It}}(\underline {s}^j~\vert ~\underline {s})=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
, so the addresses
![]() $\underline {s}^j$
are separating addresses for the triod
$\underline {s}^j$
are separating addresses for the triod
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
. The linear case works analogously and is left to the reader.
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
. The linear case works analogously and is left to the reader.
Claim 2. The result is true if
![]() $\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]\in \Omega ^-(\star \nu )$
.
$\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]\in \Omega ^-(\star \nu )$
.
Proof There exists an
![]() $n\geq 0$
such that
$n\geq 0$
such that
![]() $\mathcal {T}_{\mathcal {S}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=\textbf {stop}$
. Assume first that
$\mathcal {T}_{\mathcal {S}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=\textbf {stop}$
. Assume first that
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched. The image triod
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched. The image triod
![]() $[\underline {u}^1,\underline {u}^2,\underline {u}^3]:=\mathcal {T}_{\mathcal {S}}^{\circ (n-1)}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
consists of external addresses lying in distinct sectors of the dynamical partition
$[\underline {u}^1,\underline {u}^2,\underline {u}^3]:=\mathcal {T}_{\mathcal {S}}^{\circ (n-1)}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
consists of external addresses lying in distinct sectors of the dynamical partition
![]() $\mathcal {I}$
. Therefore, there exists addresses
$\mathcal {I}$
. Therefore, there exists addresses
![]() $\underline {\tilde {s}}^i:=k_i\underline {s}$
for suitable
$\underline {\tilde {s}}^i:=k_i\underline {s}$
for suitable
![]() $k_i\in \mathbb {Z}$
such that
$k_i\in \mathbb {Z}$
such that
![]() $\underline {\tilde {s}}^i\in (\underline {u}^i,\underline {u}^{i+1})$
, and we have
$\underline {\tilde {s}}^i\in (\underline {u}^i,\underline {u}^{i+1})$
, and we have
![]() $\operatorname {\mathrm {It}}(\underline {\tilde {s}}^i~\vert ~\underline {s})=\star \nu =\mathtt {\underline {b}}[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
for every
$\operatorname {\mathrm {It}}(\underline {\tilde {s}}^i~\vert ~\underline {s})=\star \nu =\mathtt {\underline {b}}[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
for every
![]() $i\in \{1,2,3\}$
. Hence, we have proved the lemma for the image triod
$i\in \{1,2,3\}$
. Hence, we have proved the lemma for the image triod
![]() $[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
. By Claim 1, it also holds for
$[\underline {u}^1,\underline {u}^2,\underline {u}^3]$
. By Claim 1, it also holds for
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
. The linear case works analogously and is left to the reader.
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
. The linear case works analogously and is left to the reader.
Now assume that
![]() $\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]\notin \Omega ^-(\star \nu )$
, so the triod
$\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]\notin \Omega ^-(\star \nu )$
, so the triod
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
can be iterated indefinitely under
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
can be iterated indefinitely under
![]() $\mathcal {T}_{\mathcal {S}}$
. Every such triod is eventually periodic, so by Claim 1, we can assume without loss of generality that
$\mathcal {T}_{\mathcal {S}}$
. Every such triod is eventually periodic, so by Claim 1, we can assume without loss of generality that
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is periodic, say of period N. Hence,
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is periodic, say of period N. Hence,
![]() $\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is also periodic (under iteration of
$\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is also periodic (under iteration of
![]() $\mathcal {T}$
), possibly of smaller period. Let us write
$\mathcal {T}$
), possibly of smaller period. Let us write
![]() $\mathtt {\underline {b}}:=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=:\overline {\mathtt {b}_0\mathtt {b}_1\ldots \mathtt {b}_{n-1}}$
, where the indices of
$\mathtt {\underline {b}}:=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=:\overline {\mathtt {b}_0\mathtt {b}_1\ldots \mathtt {b}_{n-1}}$
, where the indices of
![]() $\mathtt {\underline {b}}$
are labeled modulo n.
$\mathtt {\underline {b}}$
are labeled modulo n.
Claim 3. For every
![]() $i\in \{1,2,3\}$
, there exists an address
$i\in \{1,2,3\}$
, there exists an address
![]() $\underline {s}^i\in \operatorname {\mathrm {cl}}(\underline {t}^i,\underline {t}^{i+1})$
satisfying
$\underline {s}^i\in \operatorname {\mathrm {cl}}(\underline {t}^i,\underline {t}^{i+1})$
satisfying
![]() $\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
.
$\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
.
Proof Our strategy for the proof is to pull back a suitable interval along the inverse branches of
![]() $\sigma $
prescribed by
$\sigma $
prescribed by
![]() $\mathtt {\underline {b}}$
to obtain a nested sequence of intervals whose intersection is an external address with the desired properties. The forward orbit
$\mathtt {\underline {b}}$
to obtain a nested sequence of intervals whose intersection is an external address with the desired properties. The forward orbit
![]() $T:=\Omega ^+(\underline {s})$
is finite, so
$T:=\Omega ^+(\underline {s})$
is finite, so
![]() $I_{\mathtt {b}_0}\setminus T$
consists of a finite number of disjoint open intervals. Write
$I_{\mathtt {b}_0}\setminus T$
consists of a finite number of disjoint open intervals. Write
![]() $J_{1,i}^{(0)}, \ldots , J_{n_i, i}^{(0)}$
for the subintervals of
$J_{1,i}^{(0)}, \ldots , J_{n_i, i}^{(0)}$
for the subintervals of
![]() $(\underline {t}^i, \underline {t}^{i+1})$
contained in
$(\underline {t}^i, \underline {t}^{i+1})$
contained in
![]() $I_{\mathtt {b}_0}\setminus T$
. Inductively, we define
$I_{\mathtt {b}_0}\setminus T$
. Inductively, we define
As
![]() $\mathcal {S}\setminus T$
is backward invariant, we have
$\mathcal {S}\setminus T$
is backward invariant, we have
![]() $J_{j.i}^{(m)}\cap T=\emptyset $
, so every set
$J_{j.i}^{(m)}\cap T=\emptyset $
, so every set
![]() $J_{j,i}^{(m)}$
is an interval by Lemma 5.6. Writing
$J_{j,i}^{(m)}$
is an interval by Lemma 5.6. Writing
![]() $[\underline {t}^{1, (j)},\underline {t}^{2, (j)},\underline {t}^{3, (j)}]:=\mathcal {T}_{\mathcal {S}}^{\circ j}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
, we have
$[\underline {t}^{1, (j)},\underline {t}^{2, (j)},\underline {t}^{3, (j)}]:=\mathcal {T}_{\mathcal {S}}^{\circ j}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
, we have
![]() $J_{j.i}^{(m)}\subseteq (\underline {t}^{i, (-m)},\underline {t}^{i+1, (-m)})$
by Lemma 5.5.
$J_{j.i}^{(m)}\subseteq (\underline {t}^{i, (-m)},\underline {t}^{i+1, (-m)})$
by Lemma 5.5.
After N pullbacks, we arrive at subintervals of the initial partition sector
![]() $I_{\mathtt {b}_0}$
satisfying
$I_{\mathtt {b}_0}$
satisfying
![]() $J_{j,i}^{(N)}\subseteq (\underline {t}^i,\underline {t}^{i+1})$
. Hence, each
$J_{j,i}^{(N)}\subseteq (\underline {t}^i,\underline {t}^{i+1})$
. Hence, each
![]() $J_{j,i}^{(N)}$
must be a subinterval of one of our initial intervals
$J_{j,i}^{(N)}$
must be a subinterval of one of our initial intervals
![]() $J_{j,i}^{(0)}$
. More precisely, we get three self-maps
$J_{j,i}^{(0)}$
. More precisely, we get three self-maps
![]() $\rho _i\colon \{1,\ldots , n_i\}\to \{1,\ldots ,n_i\}$
such that
$\rho _i\colon \{1,\ldots , n_i\}\to \{1,\ldots ,n_i\}$
such that
For each
![]() $i\in \{1,2,3\}$
, we can find a
$i\in \{1,2,3\}$
, we can find a
![]() $j_i\in \{1,\ldots , n_i\}$
and an
$j_i\in \{1,\ldots , n_i\}$
and an
![]() $l_i\in \mathbb {N}$
such that
$l_i\in \mathbb {N}$
such that
![]() $\rho _i^{\circ l_i}(j_i)=j_i$
, and setting
$\rho _i^{\circ l_i}(j_i)=j_i$
, and setting
![]() $N_i:=l_i\cdot N$
, we have
$N_i:=l_i\cdot N$
, we have
![]() $J_{j_i,i}^{(N_i)}\subset J_{j_i,i}^{(0)}$
. Furthermore, the first
$J_{j_i,i}^{(N_i)}\subset J_{j_i,i}^{(0)}$
. Furthermore, the first
![]() $N_i$
entries are the same for all
$N_i$
entries are the same for all
![]() $\underline {t}\in J_{j_i,i}^{(N_i)}$
, say equal to
$\underline {t}\in J_{j_i,i}^{(N_i)}$
, say equal to
![]() $s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}$
. Setting
$s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}$
. Setting
![]() $J_i^{(m)}:=J_{j_i,i}^{(mN_i)}$
, the
$J_i^{(m)}:=J_{j_i,i}^{(mN_i)}$
, the
![]() $J_i^{(m)}$
form a nested sequence of (open) intervals and every address
$J_i^{(m)}$
form a nested sequence of (open) intervals and every address
![]() $\underline {t}\in J_i^{(m)}$
begins with m times the sequence
$\underline {t}\in J_i^{(m)}$
begins with m times the sequence
![]() $s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}$
. We define
$s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}$
. We define
![]() $\underline {s}^i:=\overline {s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}}$
. Recall that for an address
$\underline {s}^i:=\overline {s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}}$
. Recall that for an address
![]() $\underline {t}\in \mathcal {S}$
, the cylinder sets
$\underline {t}\in \mathcal {S}$
, the cylinder sets
![]() $\{\underline {u}\in \mathcal {S}\colon u_0\ldots u_i=t_0\ldots t_i\}$
form an open neighborhood basis of
$\{\underline {u}\in \mathcal {S}\colon u_0\ldots u_i=t_0\ldots t_i\}$
form an open neighborhood basis of
![]() $\underline {t}$
. As every address
$\underline {t}$
. As every address
![]() $\underline {t}\in J_i^{(m)}$
begins with m times the sequence
$\underline {t}\in J_i^{(m)}$
begins with m times the sequence
![]() $s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}$
, we see that
$s_0^{(i)}s_1^{(i)}\ldots s_{N_i-1}^{(i)}$
, we see that
![]() $U\cap J_i^{(m)}\neq \emptyset $
for every open neighborhood U of
$U\cap J_i^{(m)}\neq \emptyset $
for every open neighborhood U of
![]() $\underline {s}^i$
and every
$\underline {s}^i$
and every
![]() $m\geq 0$
. Hence, we have
$m\geq 0$
. Hence, we have
![]() $\underline {s}^i\in \bigcap _{m\in \mathbb {N}}\text {cl}(J_i^{(m)})$
. This implies
$\underline {s}^i\in \bigcap _{m\in \mathbb {N}}\text {cl}(J_i^{(m)})$
. This implies
![]() $\sigma ^{\circ m}(\underline {s}^i)\in \overline {I_{\mathtt {b}_{m}}}$
for all
$\sigma ^{\circ m}(\underline {s}^i)\in \overline {I_{\mathtt {b}_{m}}}$
for all
![]() $m\in \mathbb {N}_0$
. However, we have
$m\in \mathbb {N}_0$
. However, we have
![]() $\sigma ^{\circ m}(\underline {s}^i)\notin \partial I_{\mathtt {b}_{m}}$
because otherwise
$\sigma ^{\circ m}(\underline {s}^i)\notin \partial I_{\mathtt {b}_{m}}$
because otherwise
![]() $\sigma ^{\circ m}(\underline {s}^i)$
would be strictly pre-periodic, which contradicts the fact that
$\sigma ^{\circ m}(\underline {s}^i)$
would be strictly pre-periodic, which contradicts the fact that
![]() $\underline {s}^i$
is periodic. Hence, we have
$\underline {s}^i$
is periodic. Hence, we have
![]() $\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
.
$\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
.
If
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched, we actually have
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched, we actually have
![]() $\underline {s}^i\in (\underline {t}^i,\underline {t}^{i+1})$
because
$\underline {s}^i\in (\underline {t}^i,\underline {t}^{i+1})$
because
![]() $\operatorname {\mathrm {It}}(\underline {t}^i~\vert ~\underline {s})\neq \mathtt {\underline {b}}$
for all i. If instead
$\operatorname {\mathrm {It}}(\underline {t}^i~\vert ~\underline {s})\neq \mathtt {\underline {b}}$
for all i. If instead
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is linear with
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is linear with
![]() $\underline {t}^j$
in the middle, we have
$\underline {t}^j$
in the middle, we have
![]() $\underline {s}^{j+1}\in (\underline {t}^{j+1},\underline {t}^{j+2})$
because
$\underline {s}^{j+1}\in (\underline {t}^{j+1},\underline {t}^{j+2})$
because
![]() $\operatorname {\mathrm {It}}(\underline {s}^{j+1}~\vert ~\underline {s})=\mathtt {\underline {b}}$
is distinct from both
$\operatorname {\mathrm {It}}(\underline {s}^{j+1}~\vert ~\underline {s})=\mathtt {\underline {b}}$
is distinct from both
![]() $\operatorname {\mathrm {It}}(\underline {t}^{j+1}~\vert ~\underline {s})$
and
$\operatorname {\mathrm {It}}(\underline {t}^{j+1}~\vert ~\underline {s})$
and
![]() $\operatorname {\mathrm {It}}(\underline {t}^{j+2}~\vert ~\underline {s})$
. Hence,
$\operatorname {\mathrm {It}}(\underline {t}^{j+2}~\vert ~\underline {s})$
. Hence,
![]() $\underline {t}^j$
and
$\underline {t}^j$
and
![]() $\underline {s}^{j+1}$
form separating external addresses in this case. This finishes the proof of the ‘only if’ direction.
$\underline {s}^{j+1}$
form separating external addresses in this case. This finishes the proof of the ‘only if’ direction.
Let us now prove the other direction. Assume first that there exists a (pre-)periodic
![]() $\mathtt {\underline {b}}\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
and three distinct (pre-)periodic external addresses
$\mathtt {\underline {b}}\in \mathbb {Z}^{\mathbb {N}}\cup \Omega ^-(\star \nu )$
and three distinct (pre-)periodic external addresses
![]() $\underline {s}^1, \underline {s}^2, \underline {s}^3\in \mathcal {S}$
such that
$\underline {s}^1, \underline {s}^2, \underline {s}^3\in \mathcal {S}$
such that
![]() $\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
and
$\operatorname {\mathrm {It}}(\underline {s}^i~\vert ~\underline {s})=\mathtt {\underline {b}}$
and
![]() $\underline {s}^i\in (\underline {t}^i,\underline {t}^{i+1})$
. We want to see that
$\underline {s}^i\in (\underline {t}^i,\underline {t}^{i+1})$
. We want to see that
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched with
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched with
![]() $\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=\mathtt {\underline {b}}$
. Assume to the contrary that
$\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]=\mathtt {\underline {b}}$
. Assume to the contrary that
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched with
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is branched with
![]() $\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]\neq \mathtt {\underline {b}}$
. By the above, there are three distinct (pre-)periodic external addresses
$\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]\neq \mathtt {\underline {b}}$
. By the above, there are three distinct (pre-)periodic external addresses
![]() $\underline {\tilde {s}}^1, \underline {\tilde {s}}^2, \underline {\tilde {s}}^3\in \mathcal {S}$
such that
$\underline {\tilde {s}}^1, \underline {\tilde {s}}^2, \underline {\tilde {s}}^3\in \mathcal {S}$
such that
![]() $\operatorname {\mathrm {It}}(\underline {\tilde {s}}^i~\vert ~\underline {s})=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
and
$\operatorname {\mathrm {It}}(\underline {\tilde {s}}^i~\vert ~\underline {s})=\mathtt {\underline {b}}[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
and
![]() $\underline {\tilde {s}}^i\in (\underline {t}^i,\underline {t}^{i+1})$
. This contradicts Lemma 5.7 because the sets
$\underline {\tilde {s}}^i\in (\underline {t}^i,\underline {t}^{i+1})$
. This contradicts Lemma 5.7 because the sets
![]() $\{\underline {s}^i\}$
and
$\{\underline {s}^i\}$
and
![]() $\{\underline {\tilde {s}}^j\}$
would not be unlinked. The same lemma leads to a contradiction if we assume that
$\{\underline {\tilde {s}}^j\}$
would not be unlinked. The same lemma leads to a contradiction if we assume that
![]() $[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is linear. The linear case works analogously and is left to the reader.
$[\underline {t}^1,\underline {t}^2,\underline {t}^3]$
is linear. The linear case works analogously and is left to the reader.
Let us translate Lemma 5.8 into the language of dynamic rays and their landing points. This requires Lemma 5.1 which is why we prove it now.
Proof Proof of Lemma 5.1
The formal vertex set
![]() $V_\nu $
is forward invariant under
$V_\nu $
is forward invariant under
![]() $\sigma $
because
$\sigma $
because
![]() $\Omega ^+(\star \nu )$
is forward invariant and
$\Omega ^+(\star \nu )$
is forward invariant and
![]() $\sigma (\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}))=\mathtt {\underline {b}}(\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}])$
as long as
$\sigma (\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}))=\mathtt {\underline {b}}(\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}])$
as long as
![]() $\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]\neq $
stop. Also, if
$\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]\neq $
stop. Also, if
![]() $\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]=\textbf {stop}$
, then
$\mathcal {T}{\kern1.5pt}[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]=\textbf {stop}$
, then
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})=\star \nu \in V_\nu $
.
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})=\star \nu \in V_\nu $
.
For the proof of
![]() $(2)$
, assume to the contrary that there exists a triod
$(2)$
, assume to the contrary that there exists a triod
![]() $[\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}]$
with
$[\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}]$
with
![]() $\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}\in \Omega ^+(\star \nu )$
and
$\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}\in \Omega ^+(\star \nu )$
and
![]() $\mathtt {\underline {b}}(\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}})\notin \mathcal {S}_\nu $
. Because
$\mathtt {\underline {b}}(\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}})\notin \mathcal {S}_\nu $
. Because
![]() $\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}$
are all (pre-)periodic, so is
$\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}$
are all (pre-)periodic, so is
![]() $\mathtt {\underline {b}}(\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}})$
, and we must have
$\mathtt {\underline {b}}(\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}})$
, and we must have
![]() $\mathtt {\underline {b}}(\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}})=k_1\ldots k_n\nu $
(because all other (pre-)periodic sequences are contained in
$\mathtt {\underline {b}}(\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}})=k_1\ldots k_n\nu $
(because all other (pre-)periodic sequences are contained in
![]() $\mathcal {S}_\nu $
). Iterating forward n times, we obtain another triod
$\mathcal {S}_\nu $
). Iterating forward n times, we obtain another triod
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]:=\mathcal {T}^{{\kern1.5pt}\circ n}[\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}]$
with
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]:=\mathcal {T}^{{\kern1.5pt}\circ n}[\tilde {\mathtt {\underline {t}}},\tilde {\mathtt {\underline {u}}},\tilde {\mathtt {\underline {v}}}]$
with
![]() $\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\in \Omega ^+(\nu )$
and
$\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}\in \Omega ^+(\nu )$
and
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})=\nu $
. We can assume without loss of generality that
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})=\nu $
. We can assume without loss of generality that
![]() $\mathtt {\underline {t}}=\sigma ^{\circ j}(\nu )$
,
$\mathtt {\underline {t}}=\sigma ^{\circ j}(\nu )$
,
![]() $\mathtt {\underline {u}}=\sigma ^{\circ k}(\nu )$
, and
$\mathtt {\underline {u}}=\sigma ^{\circ k}(\nu )$
, and
![]() $\mathtt {\underline {v}}=\sigma ^{\circ l}(\nu )$
, where
$\mathtt {\underline {v}}=\sigma ^{\circ l}(\nu )$
, where
![]() $j,k>0$
and
$j,k>0$
and
![]() $l\geq 0$
. The triod
$l\geq 0$
. The triod
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
might be branched or linear. In both cases, by passing to an associated triod of external addresses, Lemma 5.8 guarantees the existence of external addresses
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
might be branched or linear. In both cases, by passing to an associated triod of external addresses, Lemma 5.8 guarantees the existence of external addresses
![]() $\underline {s}',\underline {t},\underline {u}\in \mathcal {S}$
with the following properties.
$\underline {s}',\underline {t},\underline {u}\in \mathcal {S}$
with the following properties.
-
• We have
 $\operatorname {\mathrm {It}}(\underline {s}'~\vert ~\underline {s})=\nu $
,
$\operatorname {\mathrm {It}}(\underline {s}'~\vert ~\underline {s})=\nu $
,
 $\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})=\sigma ^{\circ j}(\nu )=\mathtt {\underline {t}}$
and
$\operatorname {\mathrm {It}}(\underline {t}~\vert ~\underline {s})=\sigma ^{\circ j}(\nu )=\mathtt {\underline {t}}$
and
 $\operatorname {\mathrm {It}}(\underline {u}~\vert ~\underline {s})=\sigma ^{\circ k}(\nu )=\mathtt {\underline {u}}$
.
$\operatorname {\mathrm {It}}(\underline {u}~\vert ~\underline {s})=\sigma ^{\circ k}(\nu )=\mathtt {\underline {u}}$
. -
• We have
 $\underline {t}\in (\underline {s},\underline {s}')$
and
$\underline {t}\in (\underline {s},\underline {s}')$
and
 $\underline {u}\in (\underline {s}',\underline {s})$
.
$\underline {u}\in (\underline {s}',\underline {s})$
.
By Proposition 2.13, the dynamic rays
![]() $g_{\underline {s}}$
and
$g_{\underline {s}}$
and
![]() $g_{\underline {s}'}$
land at
$g_{\underline {s}'}$
land at
![]() $0$
, while
$0$
, while
![]() $g_{\underline {t}}$
lands at
$g_{\underline {t}}$
lands at
![]() $p=E_{\lambda }^{\circ j}(0)$
and
$p=E_{\lambda }^{\circ j}(0)$
and
![]() $g_{\underline {u}}$
lands at
$g_{\underline {u}}$
lands at
![]() $q=E_{\lambda }^{\circ k}(0)$
. By Lemma 2.9, the relations
$q=E_{\lambda }^{\circ k}(0)$
. By Lemma 2.9, the relations
![]() $\underline {t}\in (\underline {s},\underline {s}')$
and
$\underline {t}\in (\underline {s},\underline {s}')$
and
![]() $\underline {u}\in (\underline {s}',\underline {s})$
imply that p and q are contained in different connected components of
$\underline {u}\in (\underline {s}',\underline {s})$
imply that p and q are contained in different connected components of
![]() $\mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {s}})\cup \operatorname {\mathrm {Tr}}(g_{\underline {s}'})\cup \{0\})$
. However then, for one of these points, say p, the itineraries of the pre-images of p have different initial entries with respect to the dynamical partitions
$\mathbb {C}\setminus (\operatorname {\mathrm {Tr}}(g_{\underline {s}})\cup \operatorname {\mathrm {Tr}}(g_{\underline {s}'})\cup \{0\})$
. However then, for one of these points, say p, the itineraries of the pre-images of p have different initial entries with respect to the dynamical partitions
![]() $\mathcal {D}$
induced by
$\mathcal {D}$
induced by
![]() $g_{\underline {s}}$
and
$g_{\underline {s}}$
and
![]() $\mathcal {D}'$
induced by
$\mathcal {D}'$
induced by
![]() $g_{\underline {s}'}$
. At least one pre-image of p is itself a post-singular point and it has different itineraries with respect to the two dynamical partitions, which contradicts Lemma 4.1.
$g_{\underline {s}'}$
. At least one pre-image of p is itself a post-singular point and it has different itineraries with respect to the two dynamical partitions, which contradicts Lemma 4.1.
Finally, let us prove
![]() $(3)$
. We can assume that
$(3)$
. We can assume that
![]() $[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is branched because otherwise, the middle point of the triod is contained in
$[\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}}]$
is branched because otherwise, the middle point of the triod is contained in
![]() $V_\nu $
anyway. Let
$V_\nu $
anyway. Let
![]() $T:=(\underline {t}^i)_{i\in I}$
,
$T:=(\underline {t}^i)_{i\in I}$
,
![]() $U:=(\underline {u}^j)_{j\in J}$
and
$U:=(\underline {u}^j)_{j\in J}$
and
![]() $V:=(\underline {v}^k)_{k\in K}$
be the sets of external addresses with itinerary
$V:=(\underline {v}^k)_{k\in K}$
be the sets of external addresses with itinerary
![]() $\mathtt {\underline {t}}$
,
$\mathtt {\underline {t}}$
,
![]() $\mathtt {\underline {u}}$
, and
$\mathtt {\underline {u}}$
, and
![]() $\mathtt {\underline {v}}$
, respectively. By Lemma 5.8 and Lemma 5.7, there are three external addresses
$\mathtt {\underline {v}}$
, respectively. By Lemma 5.8 and Lemma 5.7, there are three external addresses
![]() $\underline {s}^1,\underline {s}^2,\underline {s}^3$
(without loss of generality indexed with respect to their cyclic order) with itinerary
$\underline {s}^1,\underline {s}^2,\underline {s}^3$
(without loss of generality indexed with respect to their cyclic order) with itinerary
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
such that
$\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
such that
![]() $T\subset (\underline {s}^1,\underline {s}^2)$
,
$T\subset (\underline {s}^1,\underline {s}^2)$
,
![]() $U\subset (\underline {s}^2,\underline {s}^3)$
, and
$U\subset (\underline {s}^2,\underline {s}^3)$
, and
![]() $V\subset (\underline {s}^3,\underline {s}^1)$
. If
$V\subset (\underline {s}^3,\underline {s}^1)$
. If
![]() $\mathtt {\underline {t}}\in \Omega ^+(\star \nu )$
, we set
$\mathtt {\underline {t}}\in \Omega ^+(\star \nu )$
, we set
![]() $\mathtt {\underline {t}}':=\mathtt {\underline {t}}$
. Otherwise,
$\mathtt {\underline {t}}':=\mathtt {\underline {t}}$
. Otherwise,
![]() $\mathtt {\underline {t}}$
is the branch point of a triod
$\mathtt {\underline {t}}$
is the branch point of a triod
![]() $[\mathtt {\underline {t}}^1,\mathtt {\underline {t}}^2,\mathtt {\underline {t}}^3]$
of post-singular points
$[\mathtt {\underline {t}}^1,\mathtt {\underline {t}}^2,\mathtt {\underline {t}}^3]$
of post-singular points
![]() $\mathtt {\underline {t}}^i\in \Omega ^+(\star \nu )$
and by Lemma 5.8, we can find an external address
$\mathtt {\underline {t}}^i\in \Omega ^+(\star \nu )$
and by Lemma 5.8, we can find an external address
![]() $\underline {t}\in (\underline {s}^1,\underline {s}^2)$
with itinerary
$\underline {t}\in (\underline {s}^1,\underline {s}^2)$
with itinerary
![]() $\mathtt {\underline {t}}^j$
for a suitable value of
$\mathtt {\underline {t}}^j$
for a suitable value of
![]() $j\in \{1,2,3\}$
. We set
$j\in \{1,2,3\}$
. We set
![]() $\mathtt {\underline {t}}':=\mathtt {\underline {t}}^j$
. Proceeding with
$\mathtt {\underline {t}}':=\mathtt {\underline {t}}^j$
. Proceeding with
![]() $\mathtt {\underline {u}}$
and
$\mathtt {\underline {u}}$
and
![]() $\mathtt {\underline {v}}$
in the same way, we obtain a triod
$\mathtt {\underline {v}}$
in the same way, we obtain a triod
![]() $[\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}']$
of post-singular points
$[\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}']$
of post-singular points
![]() $\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}'\in \Omega ^+(\star \nu )$
, and it follows from Lemma 5.8 (the if-direction) that
$\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}'\in \Omega ^+(\star \nu )$
, and it follows from Lemma 5.8 (the if-direction) that
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}')=\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
. We have
$\mathtt {\underline {b}}(\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}')=\mathtt {\underline {b}}(\mathtt {\underline {t}},\mathtt {\underline {u}},\mathtt {\underline {v}})$
. We have
![]() $\mathtt {\underline {b}}(\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}')\in V_\nu $
by definition of the formal vertex set.
$\mathtt {\underline {b}}(\mathtt {\underline {t}}',\mathtt {\underline {u}}',\mathtt {\underline {v}}')\in V_\nu $
by definition of the formal vertex set.
Definition 5.9. (Separating sets)
If
![]() $v=v_{\mathtt {\underline {t}}}$
is a pre-singular vertex,
$v=v_{\mathtt {\underline {t}}}$
is a pre-singular vertex,
 $$ \begin{align*} A_{v}:=\bigcup_{\operatorname{It}(\underline{t}\,\vert\,\underline{s})=\mathtt{\underline{t}}}\operatorname{\mathrm{Tr}}(g_{\underline{t}})\cup U_{\mathtt{\underline{t}}}. \end{align*} $$
$$ \begin{align*} A_{v}:=\bigcup_{\operatorname{It}(\underline{t}\,\vert\,\underline{s})=\mathtt{\underline{t}}}\operatorname{\mathrm{Tr}}(g_{\underline{t}})\cup U_{\mathtt{\underline{t}}}. \end{align*} $$
If v is not a pre-singular vertex,
 $$ \begin{align*} A_{v}:=\bigcup_{\operatorname{It}(\underline{t}\,\vert\,\underline{s})=\mathtt{\underline{t}}}\operatorname{\mathrm{Tr}}(g_{\underline{t}})\cup\{v\}. \end{align*} $$
$$ \begin{align*} A_{v}:=\bigcup_{\operatorname{It}(\underline{t}\,\vert\,\underline{s})=\mathtt{\underline{t}}}\operatorname{\mathrm{Tr}}(g_{\underline{t}})\cup\{v\}. \end{align*} $$
It is clear (by the properties (1) and (2) imposed on U) that if
![]() $v,w\in V$
are different vertices, then
$v,w\in V$
are different vertices, then
![]() $A_v\cap A_w=\emptyset $
. See Figure 3 for a sketch of the separating sets
$A_v\cap A_w=\emptyset $
. See Figure 3 for a sketch of the separating sets
![]() $A_v$
for a particularly simple psf exponential map.
$A_v$
for a particularly simple psf exponential map.
Figure 3 Sketch of the separating sets
![]() $A_v$
associated to the embedded vertices for the exponential map
$A_v$
associated to the embedded vertices for the exponential map
![]() $E_{i\pi }$
.
$E_{i\pi }$
.
Lemma 5.10. (Separating dynamic rays)
Let
![]() $[p,q,r]$
be a triod of vertex points. The triod
$[p,q,r]$
be a triod of vertex points. The triod
![]() $[p,q,r]$
is linear with p in the middle if and only if q and r lie in different connected components of
$[p,q,r]$
is linear with p in the middle if and only if q and r lie in different connected components of
![]() $\mathbb {C}\setminus A_p$
, and it is branched with branch point
$\mathbb {C}\setminus A_p$
, and it is branched with branch point
![]() $b=b[p,q,r]\in V$
if and only if p, q, and r lie in different connected components of
$b=b[p,q,r]\in V$
if and only if p, q, and r lie in different connected components of
![]() $\mathbb {C}\setminus A_b$
.
$\mathbb {C}\setminus A_b$
.
Proof This is just a matter of translating Lemma 5.8 and Lemma 5.1 into the language of dynamic rays and their landing points using Lemma 2.9 and Proposition 2.13.
We continue our construction of homotopy Hubbard trees. Choose a point
![]() $p_0\in \partial U\setminus \operatorname {\mathrm {Tr}}(g_{\underline {s}})$
and write
$p_0\in \partial U\setminus \operatorname {\mathrm {Tr}}(g_{\underline {s}})$
and write
![]() $p_{\star \nu , j}$
for the unique pre-image of p (under
$p_{\star \nu , j}$
for the unique pre-image of p (under
![]() $E_{\lambda }$
) in the sector
$E_{\lambda }$
) in the sector
![]() $D_j$
of the dynamical partition. We choose disjoint arcs
$D_j$
of the dynamical partition. We choose disjoint arcs
![]() $\gamma _{p_{\star \nu ,j}}\colon [0,1]\to U_{\star \nu }$
from
$\gamma _{p_{\star \nu ,j}}\colon [0,1]\to U_{\star \nu }$
from
![]() $v_{\star \nu }$
to
$v_{\star \nu }$
to
![]() $p_{\star \nu ,j}$
such that
$p_{\star \nu ,j}$
such that
![]() $\gamma _{p_{\star \nu ,j}}((0,1))\subset \text {int}(U_{\star \nu })$
. These curves are there to normalize the ends of the edges of the yet to be constructed homotopy Hubbard tree that have
$\gamma _{p_{\star \nu ,j}}((0,1))\subset \text {int}(U_{\star \nu })$
. These curves are there to normalize the ends of the edges of the yet to be constructed homotopy Hubbard tree that have
![]() $v_{\star \nu }$
as an endpoint. For a pre-singular vertex
$v_{\star \nu }$
as an endpoint. For a pre-singular vertex
![]() $v_{\mathtt {\underline {t}}}$
with
$v_{\mathtt {\underline {t}}}$
with
![]() $\mathtt {\underline {t}}=k_1\ldots k_n\star \nu $
, we define the pulled-back path
$\mathtt {\underline {t}}=k_1\ldots k_n\star \nu $
, we define the pulled-back path
![]() $\gamma _{p_{\mathtt {\underline {t}},j}}:=\log _{\underline {s},k_1}\ldots \log _{\underline {s},k_n}(\gamma _{\star \nu ,j})$
with endpoints
$\gamma _{p_{\mathtt {\underline {t}},j}}:=\log _{\underline {s},k_1}\ldots \log _{\underline {s},k_n}(\gamma _{\star \nu ,j})$
with endpoints
![]() $v_{\mathtt {\underline {t}}}$
and
$v_{\mathtt {\underline {t}}}$
and
![]() $p_{\mathtt {\underline {t}},j}$
. The points
$p_{\mathtt {\underline {t}},j}$
. The points
![]() $p_{\mathtt {\underline {t}},j}$
are just auxiliary points that will lie on the interior of an edge at the end of the construction.
$p_{\mathtt {\underline {t}},j}$
are just auxiliary points that will lie on the interior of an edge at the end of the construction.
We call an arc
![]() $\gamma \colon [0,1]\to \mathbb {C}$
between two different points
$\gamma \colon [0,1]\to \mathbb {C}$
between two different points
![]() $v,w\in V$
allowable if the following conditions are satisfied.
$v,w\in V$
allowable if the following conditions are satisfied.
-
• If
 $r\in V$
is not a pre-singular vertex, then either
$r\in V$
is not a pre-singular vertex, then either
 $\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\emptyset $
or
$\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\emptyset $
or
 $\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\{r\}$
.
$\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\{r\}$
. -
• If
 $r=v_{\mathtt {\underline {t}}}\in V$
is a pre-singular vertex, then either
$r=v_{\mathtt {\underline {t}}}\in V$
is a pre-singular vertex, then either
 $\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\emptyset $
or
$\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\emptyset $
or
 $\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\operatorname {\mathrm {Tr}}(\gamma _{p_{\mathtt {\underline {t}},i}})$
for some
$\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\operatorname {\mathrm {Tr}}(\gamma _{p_{\mathtt {\underline {t}},i}})$
for some
 $i\in \mathbb {Z}$
if r is one of the endpoints of
$i\in \mathbb {Z}$
if r is one of the endpoints of
 $\gamma $
or
$\gamma $
or
 $\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\operatorname {\mathrm {Tr}}(\gamma _{p_{\mathtt {\underline {t}},i}})\cup \operatorname {\mathrm {Tr}}(\gamma _{p_{\mathtt {\underline {t}},j}})$
for indices
$\operatorname {\mathrm {Tr}}(\gamma )\cap A_{r}=\operatorname {\mathrm {Tr}}(\gamma _{p_{\mathtt {\underline {t}},i}})\cup \operatorname {\mathrm {Tr}}(\gamma _{p_{\mathtt {\underline {t}},j}})$
for indices
 $i\neq j$
if r lies in the interior of the path.
$i\neq j$
if r lies in the interior of the path.
An allowable arc
![]() $\gamma $
satisfying
$\gamma $
satisfying
![]() $\gamma ^{-1}(V)=\{0,1\}$
is called an edge. We call two vertices incident if they can be connected by an edge. Note that every allowable arc is a concatenation of finitely many edges; conversely, concatenating edges of a finite acyclic path always yields an allowable arc.
$\gamma ^{-1}(V)=\{0,1\}$
is called an edge. We call two vertices incident if they can be connected by an edge. Note that every allowable arc is a concatenation of finitely many edges; conversely, concatenating edges of a finite acyclic path always yields an allowable arc.
Lemma 5.11. (Existence and uniqueness of allowable arcs)
For any pair of distinct vertices
![]() $w,w'\in V$
, there exists an allowable arc
$w,w'\in V$
, there exists an allowable arc
![]() $\gamma \colon [0,1]\to \mathbb {C}$
with
$\gamma \colon [0,1]\to \mathbb {C}$
with
![]() $\gamma (0)=w$
and
$\gamma (0)=w$
and
![]() $\gamma (1)=w'$
. If
$\gamma (1)=w'$
. If
![]() $\tilde {\gamma }\colon [0,1]\to \mathbb {C}$
is another allowable arc from w to
$\tilde {\gamma }\colon [0,1]\to \mathbb {C}$
is another allowable arc from w to
![]() $w'$
, then
$w'$
, then
![]() $\gamma $
and
$\gamma $
and
![]() $\tilde {\gamma }$
are homotopic rel
$\tilde {\gamma }$
are homotopic rel
![]() $\bigcup _{v\in V} A_{v}$
.
$\bigcup _{v\in V} A_{v}$
.
Proof Let D be a connected component of
![]() $\mathbb {C}\setminus \bigcup _{v\in V} A_{v}$
. We start by investigating the topology of D and
$\mathbb {C}\setminus \bigcup _{v\in V} A_{v}$
. We start by investigating the topology of D and
![]() $\partial D$
. It is well known that if
$\partial D$
. It is well known that if
![]() $A\subset \overline {\mathbb {C}}$
is closed and connected, every connected component of
$A\subset \overline {\mathbb {C}}$
is closed and connected, every connected component of
![]() $\overline {\mathbb {C}}\setminus A$
is simply connected. As
$\overline {\mathbb {C}}\setminus A$
is simply connected. As
![]() $\operatorname {\mathrm {cl}}_{\overline {\mathbb {C}}}(\bigcup _{v\in V} A_{v})$
is closed and connected, D is simply connected. Let B be a connected component of
$\operatorname {\mathrm {cl}}_{\overline {\mathbb {C}}}(\bigcup _{v\in V} A_{v})$
is closed and connected, D is simply connected. Let B be a connected component of
![]() $\partial D$
. We have
$\partial D$
. We have
![]() $B\subset \partial A_v$
for some
$B\subset \partial A_v$
for some
![]() $v\in V$
. If
$v\in V$
. If
![]() $v=v_{\mathtt {\underline {t}}}$
is a pre-singular vertex, then there exists a continuous bijection
$v=v_{\mathtt {\underline {t}}}$
is a pre-singular vertex, then there exists a continuous bijection
![]() $\Gamma \colon (-\infty ,\infty )\to B$
such that
$\Gamma \colon (-\infty ,\infty )\to B$
such that
![]() $\lim _{t\to -\infty }\Gamma (t)=\lim _{t\to +\infty }\Gamma (t)=\infty $
(in
$\lim _{t\to -\infty }\Gamma (t)=\lim _{t\to +\infty }\Gamma (t)=\infty $
(in
![]() $\overline {\mathbb {C}}$
) and
$\overline {\mathbb {C}}$
) and
![]() $\Gamma (0)=p_{\mathtt {\underline {t}},j}$
for some
$\Gamma (0)=p_{\mathtt {\underline {t}},j}$
for some
![]() $j\in \mathbb {Z}$
. We call
$j\in \mathbb {Z}$
. We call
![]() $p_{\mathtt {\underline {t}},j}$
the distinguished boundary point of D on
$p_{\mathtt {\underline {t}},j}$
the distinguished boundary point of D on
![]() $A_v$
. If v is not pre-singular, and there is only one dynamic ray g landing at v, then we have
$A_v$
. If v is not pre-singular, and there is only one dynamic ray g landing at v, then we have
![]() $B=\partial D\cap A_v =\operatorname {\mathrm {Tr}}(g)\cup \{v\}$
. If there are at least two dynamic rays landing at v, we have
$B=\partial D\cap A_v =\operatorname {\mathrm {Tr}}(g)\cup \{v\}$
. If there are at least two dynamic rays landing at v, we have
![]() $B=\partial D\cap A_v\operatorname {\mathrm {Tr}}(g)\cup \operatorname {\mathrm {Tr}}(g')\cup \{v\}$
for some rays
$B=\partial D\cap A_v\operatorname {\mathrm {Tr}}(g)\cup \operatorname {\mathrm {Tr}}(g')\cup \{v\}$
for some rays
![]() $g,g'$
landing at v. In both cases, we call v the distinguished boundary point of D on
$g,g'$
landing at v. In both cases, we call v the distinguished boundary point of D on
![]() $A_v$
.
$A_v$
.
We claim that
![]() $\partial D$
has at most two connected components. Assume to the contrary that there are vertices
$\partial D$
has at most two connected components. Assume to the contrary that there are vertices
![]() $v_1,v_2,v_3\in V$
such that
$v_1,v_2,v_3\in V$
such that
![]() $\partial D\cap A_{v_i}\neq \emptyset $
for all i. Then, we can connect any two distinct
$\partial D\cap A_{v_i}\neq \emptyset $
for all i. Then, we can connect any two distinct
![]() $v_i$
and
$v_i$
and
![]() $v_j$
by a curve
$v_j$
by a curve
![]() $\gamma _{(i,j)}$
such that
$\gamma _{(i,j)}$
such that
![]() $\operatorname {\mathrm {Tr}}(\gamma )\cap A_v=\emptyset $
for all
$\operatorname {\mathrm {Tr}}(\gamma )\cap A_v=\emptyset $
for all
![]() $v\in V\setminus \{v_i,v_j\}$
. Consider the triod
$v\in V\setminus \{v_i,v_j\}$
. Consider the triod
![]() $[v_1,v_2,v_3]$
. If it is linear with middle point
$[v_1,v_2,v_3]$
. If it is linear with middle point
![]() $v_i$
, then
$v_i$
, then
![]() $A_{v_{i-1}}$
and
$A_{v_{i-1}}$
and
![]() $A_{v_{i+1}}$
are separated by
$A_{v_{i+1}}$
are separated by
![]() $A_{v_i}$
by Lemma 5.10, and if
$A_{v_i}$
by Lemma 5.10, and if
![]() $[v_1,v_2,v_3]$
is branched with branch point b, then each pair
$[v_1,v_2,v_3]$
is branched with branch point b, then each pair
![]() $A_{v_i}$
and
$A_{v_i}$
and
![]() $A_{v_j}$
is separated by
$A_{v_j}$
is separated by
![]() $A_b$
by Lemma 5.10. In both cases, we get a contradiction. Therefore, there are only three possibilities for the topology of
$A_b$
by Lemma 5.10. In both cases, we get a contradiction. Therefore, there are only three possibilities for the topology of
![]() $(D,\partial D)$
: there exists a homeomorphism
$(D,\partial D)$
: there exists a homeomorphism
![]() $\varphi \colon (D,\partial D)\to (\Omega _i,\partial \Omega _i)$
, that is, a homeomorphism
$\varphi \colon (D,\partial D)\to (\Omega _i,\partial \Omega _i)$
, that is, a homeomorphism
![]() $\varphi \colon \overline {D}\to \overline {\Omega _i}$
satisfying
$\varphi \colon \overline {D}\to \overline {\Omega _i}$
satisfying
![]() $\varphi (\partial D)=\partial \Omega _i$
for exactly one of three uniformizing domains
$\varphi (\partial D)=\partial \Omega _i$
for exactly one of three uniformizing domains
![]() $\Omega _i\subset \mathbb {C}$
, where:
$\Omega _i\subset \mathbb {C}$
, where:
-
(1)
 $\Omega _1:=\{z\in \mathbb {C}\colon \operatorname {Re}(z)>0\}$
is the right half-plane;
$\Omega _1:=\{z\in \mathbb {C}\colon \operatorname {Re}(z)>0\}$
is the right half-plane; -
(2)
 $\Omega _2:=\{z\in \mathbb {C}\colon \operatorname {Re}(z)>0\}\setminus [1,+\infty )$
is the slit right half-plane;
$\Omega _2:=\{z\in \mathbb {C}\colon \operatorname {Re}(z)>0\}\setminus [1,+\infty )$
is the slit right half-plane; -
(3) and
 $\Omega _3:=\{z\in \mathbb {C}\colon 0<\operatorname {Re}(z)<1\}$
is a vertical strip.
$\Omega _3:=\{z\in \mathbb {C}\colon 0<\operatorname {Re}(z)<1\}$
is a vertical strip.
Let us now prove the existence and uniqueness of allowable arcs. First, consider the special case that there exists a connected component D of
![]() $\mathbb {C}\setminus \bigcup _{v\in V} A_{v}$
such that
$\mathbb {C}\setminus \bigcup _{v\in V} A_{v}$
such that
![]() $\partial D\cap A_w\neq \emptyset $
and
$\partial D\cap A_w\neq \emptyset $
and
![]() $\partial D\cap A_{w'}\neq \emptyset $
. Let
$\partial D\cap A_{w'}\neq \emptyset $
. Let
![]() $p_w,p_w'\in \partial D$
be the distinguished boundary points. The domain D is of type (2) or (3), so there exists an arc
$p_w,p_w'\in \partial D$
be the distinguished boundary points. The domain D is of type (2) or (3), so there exists an arc
![]() $\delta \colon [0,1]\to \overline {D}$
from
$\delta \colon [0,1]\to \overline {D}$
from
![]() $p_w$
to
$p_w$
to
![]() $p_w'$
such that
$p_w'$
such that
![]() $\delta ((0,1))\in D$
, and
$\delta ((0,1))\in D$
, and
![]() $\delta $
is unique up to homotopy rel
$\delta $
is unique up to homotopy rel
![]() $\bigcup _{v\in V} A_{v}$
. We obtain an edge
$\bigcup _{v\in V} A_{v}$
. We obtain an edge
![]() $\gamma $
connecting w and
$\gamma $
connecting w and
![]() $w'$
after concatenating
$w'$
after concatenating
![]() $\delta $
with
$\delta $
with
![]() $\gamma _{p_w}$
or
$\gamma _{p_w}$
or
![]() $\gamma _{p_{w'}}$
if
$\gamma _{p_{w'}}$
if
![]() $p_w\neq w$
or
$p_w\neq w$
or
![]() $p_{w'}\neq w'$
.
$p_{w'}\neq w'$
.
Finally, consider the general case and set
![]() $v_0:=w$
. Let
$v_0:=w$
. Let
![]() $E(v_0)$
be the component of
$E(v_0)$
be the component of
![]() $\mathbb {C}\setminus A_{v_0}$
containing
$\mathbb {C}\setminus A_{v_0}$
containing
![]() $w'$
, and let
$w'$
, and let
![]() $D_1$
be the unique component of
$D_1$
be the unique component of
![]() $\mathbb {C}\setminus \bigcup _{v\in V} A_{v}$
such that
$\mathbb {C}\setminus \bigcup _{v\in V} A_{v}$
such that
![]() $\partial D_1\cap A_{v_0}\neq \emptyset $
and
$\partial D_1\cap A_{v_0}\neq \emptyset $
and
![]() $D_1\subset E(v_0)$
. The component
$D_1\subset E(v_0)$
. The component
![]() $D_1$
is of type (2) or (3) because
$D_1$
is of type (2) or (3) because
![]() $E(v_0)$
contains at least the vertex
$E(v_0)$
contains at least the vertex
![]() $w'$
, so there exists
$w'$
, so there exists
![]() $v_1\in V$
such that
$v_1\in V$
such that
![]() $\partial D_1\cap A_{v_1}\neq \emptyset $
. If
$\partial D_1\cap A_{v_1}\neq \emptyset $
. If
![]() $v_1=w'$
, we are reduced to the special case. Else
$v_1=w'$
, we are reduced to the special case. Else
![]() $D_1$
is of type (3) and there is a unique component
$D_1$
is of type (3) and there is a unique component
![]() $E(v_1)\subset E(v_0)$
of
$E(v_1)\subset E(v_0)$
of
![]() $\mathbb {C}\setminus A_{v_1}$
containing
$\mathbb {C}\setminus A_{v_1}$
containing
![]() $w'$
. We continue this argument inductively, and as the number of vertices contained in
$w'$
. We continue this argument inductively, and as the number of vertices contained in
![]() $E(v_i)$
decreases in each step, we obtain a finite sequence
$E(v_i)$
decreases in each step, we obtain a finite sequence
![]() $w=v_0, v_1, \ldots , v_n=w'$
of vertices such that
$w=v_0, v_1, \ldots , v_n=w'$
of vertices such that
![]() $A_{v_{i-1}}$
and
$A_{v_{i-1}}$
and
![]() $A_{v_{i}}$
both intersect
$A_{v_{i}}$
both intersect
![]() $\partial D_i$
. The concatenation
$\partial D_i$
. The concatenation
![]() $\gamma :=\gamma _0\cdot \gamma _1\cdot \cdots \cdot \gamma _{n-1}$
, where
$\gamma :=\gamma _0\cdot \gamma _1\cdot \cdots \cdot \gamma _{n-1}$
, where
![]() $\gamma _i$
is an edge from
$\gamma _i$
is an edge from
![]() $v_i$
to
$v_i$
to
![]() $v_{i+1}$
, is an allowable path from w to
$v_{i+1}$
, is an allowable path from w to
![]() $w'$
, and it is unique up to homotopy rel
$w'$
, and it is unique up to homotopy rel
![]() $\bigcup _{v\in V} A_{v}$
because every part of
$\bigcup _{v\in V} A_{v}$
because every part of
![]() $\gamma _i$
is unique.
$\gamma _i$
is unique.
Theorem 5.12. (Existence of homotopy Hubbard trees)
For every post-singularly finite exponential map
![]() $E_{\lambda }$
, there exists a homotopy Hubbard tree.
$E_{\lambda }$
, there exists a homotopy Hubbard tree.
Proof For every pair
![]() $w,w'\in V$
of incident vertices, choose an edge
$w,w'\in V$
of incident vertices, choose an edge
![]() $e_{(w,w')}\colon [0,1]\to \mathbb {C}$
connecting w and
$e_{(w,w')}\colon [0,1]\to \mathbb {C}$
connecting w and
![]() $w'$
. We choose the unique edge
$w'$
. We choose the unique edge
![]() $e_{(0,w_0)}\colon [0,1]\to \mathbb {C}$
connecting
$e_{(0,w_0)}\colon [0,1]\to \mathbb {C}$
connecting
![]() $0$
to another vertex
$0$
to another vertex
![]() $w_0$
in such a way that it intersects
$w_0$
in such a way that it intersects
![]() $\partial U$
only at the point
$\partial U$
only at the point
![]() $p_0\in \partial U\setminus \operatorname {\mathrm {Tr}}(g_{\underline {s}})$
(see the paragraph before Lemma 5.11 for the definition of
$p_0\in \partial U\setminus \operatorname {\mathrm {Tr}}(g_{\underline {s}})$
(see the paragraph before Lemma 5.11 for the definition of
![]() $p_0$
). Define
$p_0$
). Define
 $$ \begin{align*} H:=\bigcup_{w,w'\in V~\text{incident}}\operatorname{\mathrm{Tr}}(e_{(w,w')}). \end{align*} $$
$$ \begin{align*} H:=\bigcup_{w,w'\in V~\text{incident}}\operatorname{\mathrm{Tr}}(e_{(w,w')}). \end{align*} $$
As every edge is contained in some component of
![]() $\mathbb {C}\setminus \bigcup _{v\in V}A_v$
(except possibly for its normalized ends), and every such component contains at most one edge by Lemma 5.11, different edges are disjoint (except possibly for their endpoints). Clearly, they are not homotopic rel
$\mathbb {C}\setminus \bigcup _{v\in V}A_v$
(except possibly for its normalized ends), and every such component contains at most one edge by Lemma 5.11, different edges are disjoint (except possibly for their endpoints). Clearly, they are not homotopic rel
![]() $\bigcup _{v\in V}A_v$
. The embedded graph H is connected by Lemma 5.11, and the existence of a cycle of edges would contradict uniqueness in Lemma 5.11. Hence, H is an embedded tree. Moreover, every endpoint of H is a post-singular point: every vertex
$\bigcup _{v\in V}A_v$
. The embedded graph H is connected by Lemma 5.11, and the existence of a cycle of edges would contradict uniqueness in Lemma 5.11. Hence, H is an embedded tree. Moreover, every endpoint of H is a post-singular point: every vertex
![]() $v\in V\setminus P(E_{\lambda })$
is the middle point of a triod of the form
$v\in V\setminus P(E_{\lambda })$
is the middle point of a triod of the form
![]() $[p_1,v,p_2]$
with
$[p_1,v,p_2]$
with
![]() $p_1,p_2\in P(E_{\lambda })$
and the in-tree connection of
$p_1,p_2\in P(E_{\lambda })$
and the in-tree connection of
![]() $p_1$
and
$p_1$
and
![]() $p_2$
has to contain v by Lemma 5.10 and the definition of allowable arcs.
$p_2$
has to contain v by Lemma 5.10 and the definition of allowable arcs.
Next, we want to see that
![]() $H':=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
is homotopic to H rel
$H':=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
is homotopic to H rel
![]() $P(E_{\lambda })$
. By Lemma 3.14, we can find a homotopy
$P(E_{\lambda })$
. By Lemma 3.14, we can find a homotopy
![]() $I_0$
between
$I_0$
between
![]() $H'$
and an embedded tree
$H'$
and an embedded tree
![]() $H''\subset \mathbb {C}$
rel
$H''\subset \mathbb {C}$
rel
![]() $\mathbb {C}_T\setminus \widehat {E_{\lambda }}^{-1}(U)$
, and by our choice of the edge
$\mathbb {C}_T\setminus \widehat {E_{\lambda }}^{-1}(U)$
, and by our choice of the edge
![]() $e_{(0,w_0)}$
, we can make sure that
$e_{(0,w_0)}$
, we can make sure that
![]() $H''\cap \widehat {E_{\lambda }}^{-1}(U)=H\cap \widehat {E_{\lambda }}^{-1}(U)=\bigcup _{i\in \{1,\ldots , k\}}\operatorname {\mathrm {Tr}}(\gamma _{p_{\star \nu , j_i}})$
for certain
$H''\cap \widehat {E_{\lambda }}^{-1}(U)=H\cap \widehat {E_{\lambda }}^{-1}(U)=\bigcup _{i\in \{1,\ldots , k\}}\operatorname {\mathrm {Tr}}(\gamma _{p_{\star \nu , j_i}})$
for certain
![]() $j_i\in \mathbb {Z}$
.
$j_i\in \mathbb {Z}$
.
For a vertex
![]() $v\neq v_{\star \nu }$
, the map
$v\neq v_{\star \nu }$
, the map
![]() $E_{\lambda }\colon A_v\to A_{E_{\lambda }(v)}$
is a homeomorphism, and if
$E_{\lambda }\colon A_v\to A_{E_{\lambda }(v)}$
is a homeomorphism, and if
![]() $v=v_{\mathtt {\underline {t}}}$
is pre-singular, we have
$v=v_{\mathtt {\underline {t}}}$
is pre-singular, we have
![]() $E_{\lambda }(\bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\mathtt {\underline {t}},j}))=\bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\sigma (\mathtt {\underline {t}}),j})$
. If v is not pre-singular, we have
$E_{\lambda }(\bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\mathtt {\underline {t}},j}))=\bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\sigma (\mathtt {\underline {t}}),j})$
. If v is not pre-singular, we have
![]() $H\cap A_{E_{\lambda }(v)}=\{E_{\lambda }(v)\}$
, and therefore
$H\cap A_{E_{\lambda }(v)}=\{E_{\lambda }(v)\}$
, and therefore
![]() $\widehat {E_{\lambda }}^{-1}(H)\cap A_v=\{v\}$
. If instead
$\widehat {E_{\lambda }}^{-1}(H)\cap A_v=\{v\}$
. If instead
![]() $v=v_{\mathtt {\underline {t}}}\neq v_{\star \nu }$
is pre-singular, we have
$v=v_{\mathtt {\underline {t}}}\neq v_{\star \nu }$
is pre-singular, we have
![]() $H\cap A_{E_{\lambda }(v)}\subset \bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\sigma (\mathtt {\underline {t}}),j})$
, and therefore
$H\cap A_{E_{\lambda }(v)}\subset \bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\sigma (\mathtt {\underline {t}}),j})$
, and therefore
![]() $\widehat {E_{\lambda }}^{-1}(H)\cap A_v\subset \bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\mathtt {\underline {t}},j})$
. Hence, for every pair of distinct post-singular points
$\widehat {E_{\lambda }}^{-1}(H)\cap A_v\subset \bigcup _j\operatorname {\mathrm {Tr}}(\gamma _{\mathtt {\underline {t}},j})$
. Hence, for every pair of distinct post-singular points
![]() $p,q\in P(E_{\lambda })$
, the in-tree connection
$p,q\in P(E_{\lambda })$
, the in-tree connection
![]() $[p,q]_{H''}$
is an allowable arc.
$[p,q]_{H''}$
is an allowable arc.
It follows that
![]() $V\subset H''$
, because every
$V\subset H''$
, because every
![]() $v\in V\setminus (P(E_{\lambda })\cup \{v_{\star \nu }\})$
is the branch point of a post-singular triod. Moreover, the trees H and
$v\in V\setminus (P(E_{\lambda })\cup \{v_{\star \nu }\})$
is the branch point of a post-singular triod. Moreover, the trees H and
![]() $H''$
have the same graph structure on V. To see this, observe that H is defined to contain an edge for every pair of incident vertices. Hence, vertices that are connected by an edge in
$H''$
have the same graph structure on V. To see this, observe that H is defined to contain an edge for every pair of incident vertices. Hence, vertices that are connected by an edge in
![]() $H''$
are also connected by an edge in H. Conversely, the tree
$H''$
are also connected by an edge in H. Conversely, the tree
![]() $H''$
must contain all edges in H because otherwise it would be disconnected. By the uniqueness of allowable arcs, there exists a homotopy
$H''$
must contain all edges in H because otherwise it would be disconnected. By the uniqueness of allowable arcs, there exists a homotopy
![]() $I_1$
between
$I_1$
between
![]() $H''$
and H rel
$H''$
and H rel
![]() $\bigcup _{v\in V}A_v$
. We obtain a homotopy I between H and
$\bigcup _{v\in V}A_v$
. We obtain a homotopy I between H and
![]() $H'$
rel
$H'$
rel
![]() $P(E_{\lambda })$
by concatenating
$P(E_{\lambda })$
by concatenating
![]() $I_0$
and
$I_0$
and
![]() $I_1$
.
$I_1$
.
It remains to show that the induced self-map
![]() $f:=\widehat {E_{\lambda }}\circ I^1\colon H\to H$
is expansive (see the paragraph before Definition 3.9 for the definition of expansivity). By construction, we have
$f:=\widehat {E_{\lambda }}\circ I^1\colon H\to H$
is expansive (see the paragraph before Definition 3.9 for the definition of expansivity). By construction, we have
![]() $I^1(v_{\star \nu })=-\infty $
and we deduce that
$I^1(v_{\star \nu })=-\infty $
and we deduce that
![]() $V_f=V$
for the set of marked points of the self-map f. Let
$V_f=V$
for the set of marked points of the self-map f. Let
![]() $p,q\in V_f=V$
be two different marked points of f. By construction, two vertices
$p,q\in V_f=V$
be two different marked points of f. By construction, two vertices
![]() $v_{\mathtt {\underline {t}}},v_{\mathtt {\underline {u}}}\in V\setminus \{v_{\star \nu }\}$
are contained in different branches of H at
$v_{\mathtt {\underline {t}}},v_{\mathtt {\underline {u}}}\in V\setminus \{v_{\star \nu }\}$
are contained in different branches of H at
![]() $v_{\star \nu }$
if and only if the first entries of
$v_{\star \nu }$
if and only if the first entries of
![]() $\mathtt {\underline {t}}$
and
$\mathtt {\underline {t}}$
and
![]() $\mathtt {\underline {u}}$
are different. As different vertices have different itineraries, there exists a small
$\mathtt {\underline {u}}$
are different. As different vertices have different itineraries, there exists a small
![]() $n\geq 0$
such that the itineraries of
$n\geq 0$
such that the itineraries of
![]() $f^{\circ n}(p)$
and
$f^{\circ n}(p)$
and
![]() $f^{\circ n}(q)$
have different initial entries. Hence, we have
$f^{\circ n}(q)$
have different initial entries. Hence, we have
![]() $v_{\star \nu }\in [f^{\circ n}(p),f^{\circ n}(q)]\subset f^{\circ n}[p,q]$
.
$v_{\star \nu }\in [f^{\circ n}(p),f^{\circ n}(q)]\subset f^{\circ n}[p,q]$
.
6 Classification of post-singularly finite exponential maps
Post-singularly finite exponential maps have been classified in terms of the external addresses of the dynamic rays landing at the singular value in [Reference Laubner, Schleicher and VicolLSV], and we have stated their main result in Theorem 2.14. As an application of our construction, we give another combinatorial classification of this class of maps in terms of abstract Hubbard trees. Post-singularly finite polynomials have been classified combinatorially by Poirier in [Reference PoirierP] in terms of so-called abstract Hubbard trees. These are graph-theoretic trees equipped with a self-map and certain extra information, but without an embedding into
![]() $\mathbb {C}$
. The exponential dynamical trees from Definition 4.2 come quite close to what we mean by an abstract exponential Hubbard tree. We have to add a cyclic order on the branches of the tree at each marked point to specify a homotopy type of embeddings of the tree into the complex plane.
$\mathbb {C}$
. The exponential dynamical trees from Definition 4.2 come quite close to what we mean by an abstract exponential Hubbard tree. We have to add a cyclic order on the branches of the tree at each marked point to specify a homotopy type of embeddings of the tree into the complex plane.
Definition 6.1. (Abstract exponential Hubbard tree)
An abstract exponential Hubbard tree
![]() $(H,f,B_{k_i},\angle _v)$
is an exponential dynamical tree
$(H,f,B_{k_i},\angle _v)$
is an exponential dynamical tree
![]() $(H,f,B_{k_i})$
together with a cyclic order
$(H,f,B_{k_i})$
together with a cyclic order
![]() $\angle _v$
on the set of branches of H at v for each marked point
$\angle _v$
on the set of branches of H at v for each marked point
![]() $v\in V_f\setminus \{v_T\}$
such that f preserves the cyclic order. Two abstract Hubbard trees
$v\in V_f\setminus \{v_T\}$
such that f preserves the cyclic order. Two abstract Hubbard trees
![]() $(H,f,B_{k_i},\angle _v)$
and
$(H,f,B_{k_i},\angle _v)$
and
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i}, \angle _{\tilde {v}})$
are called equivalent if they are equivalent as exponential dynamical trees and, in addition, the homeomorphism
$(\tilde {H},\tilde {f},\tilde {B}_{k_i}, \angle _{\tilde {v}})$
are called equivalent if they are equivalent as exponential dynamical trees and, in addition, the homeomorphism
![]() $\varphi \colon H\to \tilde {H}$
from Definition 4.2 can be chosen to preserve the cyclic order at marked points.
$\varphi \colon H\to \tilde {H}$
from Definition 4.2 can be chosen to preserve the cyclic order at marked points.
Let H be a homotopy Hubbard tree for the post-singularly finite exponential map
![]() $E_{\lambda }$
. In §4, we have seen that for any choice of induced self-map
$E_{\lambda }$
. In §4, we have seen that for any choice of induced self-map
![]() $f\colon H\to H$
, the triple
$f\colon H\to H$
, the triple
![]() $(H,f,B_{k_i})$
is an exponential dynamical tree. We have also seen that if
$(H,f,B_{k_i})$
is an exponential dynamical tree. We have also seen that if
![]() $\tilde {H}$
is another homotopy Hubbard tree for
$\tilde {H}$
is another homotopy Hubbard tree for
![]() $E_{\lambda }$
with choice of induced self-map
$E_{\lambda }$
with choice of induced self-map
![]() $\tilde {f}\colon \tilde {H}\to \tilde {H}$
, the exponential dynamical trees
$\tilde {f}\colon \tilde {H}\to \tilde {H}$
, the exponential dynamical trees
![]() $(H,f,B_{k_i})$
and
$(H,f,B_{k_i})$
and
![]() $(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
are equivalent. As H is embedded into the complex plane, the branches of H at a marked point
$(\tilde {H},\tilde {f},\tilde {B}_{k_i})$
are equivalent. As H is embedded into the complex plane, the branches of H at a marked point
![]() $v\in V_f\setminus \{v_T\}$
come equipped with a natural cyclic order
$v\in V_f\setminus \{v_T\}$
come equipped with a natural cyclic order
![]() $\angle _v$
(of course this also holds for
$\angle _v$
(of course this also holds for
![]() $v_T$
, but the cyclic order of edges at
$v_T$
, but the cyclic order of edges at
![]() $v_T$
is already contained in the sector information). Also, the trees H and
$v_T$
is already contained in the sector information). Also, the trees H and
![]() $\tilde {H}$
are homotopic in
$\tilde {H}$
are homotopic in
![]() $\mathbb {C}$
rel
$\mathbb {C}$
rel
![]() $P(E_{\lambda })$
, and such a homotopy preserves the cyclic order of branches at marked points. It follows that there is a well-defined map
$P(E_{\lambda })$
, and such a homotopy preserves the cyclic order of branches at marked points. It follows that there is a well-defined map
where we consider abstract exponential Hubbard trees up to equivalence. In this section, we prove that
![]() $\mathcal {F}$
is a bijection.
$\mathcal {F}$
is a bijection.
The major tool that has made classification results of this kind possible for certain classes of rational functions is Thurston’s topological characterization of rational maps. An analogous result for exponential maps has been established in [Reference Hubbard, Schleicher and ShishikuraHSS]. To state this result precisely, we need to introduce some terminology.
Convention 6.2. In the following,
![]() $\mathbb {S}^2$
denotes an oriented topological
$\mathbb {S}^2$
denotes an oriented topological
![]() $2$
-sphere with two distinguished points
$2$
-sphere with two distinguished points
![]() $0$
and
$0$
and
![]() $\infty $
. All homeomorphisms and coverings will be understood to be orientation preserving. We also write
$\infty $
. All homeomorphisms and coverings will be understood to be orientation preserving. We also write
![]() $\mathbb {R}^2=\mathbb {S}^2\setminus \{\infty \}$
.
$\mathbb {R}^2=\mathbb {S}^2\setminus \{\infty \}$
.
Definition 6.3. (Topological exponential maps)
A covering map
![]() $g\colon \mathbb {R}^2\to \mathbb {R}^2\setminus \{0\}$
is called a topological exponential map. It is called post-singularly finite if the orbit of
$g\colon \mathbb {R}^2\to \mathbb {R}^2\setminus \{0\}$
is called a topological exponential map. It is called post-singularly finite if the orbit of
![]() $0$
is finite, hence pre-periodic. The post-singular set is
$0$
is finite, hence pre-periodic. The post-singular set is
![]() $P(g):=\bigcup _{n\geq 0}g^{\circ n}(0)$
.
$P(g):=\bigcup _{n\geq 0}g^{\circ n}(0)$
.
Definition 6.4. (Thurston equivalence)
Two post-singularly finite topological exponential maps f and g with post-singular sets
![]() $P(f)$
and
$P(f)$
and
![]() $P(g)$
are called Thurston equivalent if there are two homeomorphisms
$P(g)$
are called Thurston equivalent if there are two homeomorphisms
![]() $\varphi _0,\varphi _1\colon \mathbb {R}^2\to \mathbb {R}^2$
satisfying
$\varphi _0,\varphi _1\colon \mathbb {R}^2\to \mathbb {R}^2$
satisfying
![]() $\varphi _0|_{P(f)}=\varphi _1|_{P(f)}$
and
$\varphi _0|_{P(f)}=\varphi _1|_{P(f)}$
and
![]() $P(g)=\varphi _0(P(f))=\varphi _1(P(f))$
such that the diagram
$P(g)=\varphi _0(P(f))=\varphi _1(P(f))$
such that the diagram

commutes, and
![]() $\varphi _0$
is homotopic to
$\varphi _0$
is homotopic to
![]() $\varphi _1$
relative to
$\varphi _1$
relative to
![]() $P(f)$
.
$P(f)$
.
The main result of [Reference Hubbard, Schleicher and ShishikuraHSS] is a criterion for a topological exponential map to be Thurston equivalent to a (necessarily post-singularly finite) holomorphic exponential map. There exists an equivalent holomorphic map if and only if the following obstruction does not occur; see below.
Definition 6.5. (Essential curves and Levy cycles)
Let g be a post-singularly finite topological exponential map. A simple closed curve
![]() $\gamma \subset \mathbb {S}^2\setminus (P(g)\cup \{\infty \})$
is called essential if both connected components of
$\gamma \subset \mathbb {S}^2\setminus (P(g)\cup \{\infty \})$
is called essential if both connected components of
![]() $\mathbb {S}^2\setminus \gamma $
contain at least two points of
$\mathbb {S}^2\setminus \gamma $
contain at least two points of
![]() $P(g)\cup \{\infty \}$
. A Levy cycle of g is a finite sequence of disjoint essential simple closed curves
$P(g)\cup \{\infty \}$
. A Levy cycle of g is a finite sequence of disjoint essential simple closed curves
![]() $\gamma _0$
,
$\gamma _0$
,
![]() $\gamma _1$
, … ,
$\gamma _1$
, … ,
![]() $\gamma _{m-1}$
,
$\gamma _{m-1}$
,
![]() $\gamma _m=\gamma _0$
such that for
$\gamma _m=\gamma _0$
such that for
![]() $i=0,1,\ldots ,m-1$
, some component
$i=0,1,\ldots ,m-1$
, some component
![]() $\gamma _i'$
of
$\gamma _i'$
of
![]() $g^{-1}(\gamma _{i+1})$
is homotopic to
$g^{-1}(\gamma _{i+1})$
is homotopic to
![]() $\gamma _i$
in
$\gamma _i$
in
![]() $\mathbb {R}^2$
relative to
$\mathbb {R}^2$
relative to
![]() $P(g)$
and
$P(g)$
and
![]() $g\colon \gamma _i'\to \gamma _{i+1}$
is a homeomorphism.
$g\colon \gamma _i'\to \gamma _{i+1}$
is a homeomorphism.
Let
![]() $U_i'$
be the bounded component of
$U_i'$
be the bounded component of
![]() $\mathbb {R}^2\setminus \gamma _i'$
and let
$\mathbb {R}^2\setminus \gamma _i'$
and let
![]() $U_i$
be the bounded component of
$U_i$
be the bounded component of
![]() $\mathbb {R}^2\setminus \gamma _i$
. If all restrictions
$\mathbb {R}^2\setminus \gamma _i$
. If all restrictions
![]() $g\colon \overline {U_{i'}}\to \overline {U_{i+1}}$
are homeomorphisms, then the Levy cycle is called degenerate.
$g\colon \overline {U_{i'}}\to \overline {U_{i+1}}$
are homeomorphisms, then the Levy cycle is called degenerate.
It is easy to see that for topological exponential maps, every Levy cycle is degenerate and that Levy cycles are preserved under Thurston equivalence. Furthermore, a routine hyperbolic contraction argument shows that a post-singularly finite exponential map does not have a Levy cycle. The following theorem is the main result of [Reference Hubbard, Schleicher and ShishikuraHSS].
Theorem 6.6. (Topological characterization of exponential maps)
A post-singularly finite topological exponential map is Thurston equivalent to a post-singularly finite holomorphic exponential map if and only if it does not admit a degenerate Levy cycle. The holomorphic exponential map is unique up to conjugation with an affine map.
Remark 6.7. In our parameterization
![]() $\lambda \mapsto \lambda \exp (z)$
of the exponential parameter space, with
$\lambda \mapsto \lambda \exp (z)$
of the exponential parameter space, with
![]() $\lambda \in \mathbb {C}\setminus \{0\}$
, no two distinct
$\lambda \in \mathbb {C}\setminus \{0\}$
, no two distinct
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
are affinely conjugate. By Theorem 6.6, two post-singularly finite maps
$E_{\tilde {\lambda }}$
are affinely conjugate. By Theorem 6.6, two post-singularly finite maps
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
are never Thurston equivalent for different parameters
$E_{\tilde {\lambda }}$
are never Thurston equivalent for different parameters
![]() $\lambda ,\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
.
$\lambda ,\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
.
We show that distinct psf exponential maps always yield abstract Hubbard trees that are not equivalent. For the proof, we need a result from [Reference Bielefeld, Fisher and HubbardBFH, Corollary 6.6] about extensions of maps between embedded graphs.
Lemma 6.8. (Extension of graph homeomorphisms)
Let
![]() $\Gamma _1,\Gamma _2\subset \mathbb {S}^2$
be connected embedded graphs and let
$\Gamma _1,\Gamma _2\subset \mathbb {S}^2$
be connected embedded graphs and let
![]() $f\colon \Gamma _1\to \Gamma _2$
be a homeomorphism. Then f extends to an orientation-preserving homeomorphism
$f\colon \Gamma _1\to \Gamma _2$
be a homeomorphism. Then f extends to an orientation-preserving homeomorphism
![]() $\hat {f}\colon \mathbb {S}^2\to \mathbb {S}^2$
if and only if f preserves the cyclic order of the edges at all branch points of
$\hat {f}\colon \mathbb {S}^2\to \mathbb {S}^2$
if and only if f preserves the cyclic order of the edges at all branch points of
![]() $\Gamma _1$
.
$\Gamma _1$
.
Theorem 6.9. (Different maps have non-equivalent trees)
Let
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
be two post-singularly finite exponential maps. Let H be a homotopy Hubbard tree for
$E_{\tilde {\lambda }}$
be two post-singularly finite exponential maps. Let H be a homotopy Hubbard tree for
![]() $E_{\lambda }$
and let
$E_{\lambda }$
and let
![]() $\tilde {H}$
be a homotopy Hubbard tree for
$\tilde {H}$
be a homotopy Hubbard tree for
![]() $E_{\tilde {\lambda }}$
. If H and
$E_{\tilde {\lambda }}$
. If H and
![]() $\tilde {H}$
yield the same abstract Hubbard tree, we have
$\tilde {H}$
yield the same abstract Hubbard tree, we have
![]() $\lambda =\tilde {\lambda }$
.
$\lambda =\tilde {\lambda }$
.
Proof Choose dynamic rays g (respectively
![]() $\tilde {g}$
) of
$\tilde {g}$
) of
![]() $E_{\lambda }$
(respectively
$E_{\lambda }$
(respectively
![]() $E_{\tilde {\lambda }}$
) landing at the singular value. By Proposition 4.9, we can assume without loss of generality that H (respectively
$E_{\tilde {\lambda }}$
) landing at the singular value. By Proposition 4.9, we can assume without loss of generality that H (respectively
![]() $\tilde {H}$
) does not intersect
$\tilde {H}$
) does not intersect
![]() $\operatorname {\mathrm {Tr}}(g)$
(respectively
$\operatorname {\mathrm {Tr}}(g)$
(respectively
![]() $\operatorname {\mathrm {Tr}}(\tilde {g}))$
. By hypothesis, there exists a homeomorphism
$\operatorname {\mathrm {Tr}}(\tilde {g}))$
. By hypothesis, there exists a homeomorphism
![]() $\varphi \colon H\to \tilde {H}$
that restricts to a conjugation between
$\varphi \colon H\to \tilde {H}$
that restricts to a conjugation between
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
on
$E_{\tilde {\lambda }}$
on
![]() $P(E_{\lambda })$
, and preserves the cyclic order at each marked point of H. By Lemma 6.8,
$P(E_{\lambda })$
, and preserves the cyclic order at each marked point of H. By Lemma 6.8,
![]() $\varphi $
can be extended to a homeomorphism
$\varphi $
can be extended to a homeomorphism
![]() $\varphi _0\colon \mathbb {C}\to \mathbb {C}$
and we can choose
$\varphi _0\colon \mathbb {C}\to \mathbb {C}$
and we can choose
![]() $\varphi _0$
to satisfy
$\varphi _0$
to satisfy
![]() $\varphi _0(\operatorname {\mathrm {Tr}}(g))=\operatorname {\mathrm {Tr}}(\tilde {g})$
. In analogy to Lemma 3.5, one shows that there exists a lift
$\varphi _0(\operatorname {\mathrm {Tr}}(g))=\operatorname {\mathrm {Tr}}(\tilde {g})$
. In analogy to Lemma 3.5, one shows that there exists a lift
![]() $\varphi _1\colon \mathbb {C}\to \mathbb {C}$
of
$\varphi _1\colon \mathbb {C}\to \mathbb {C}$
of
![]() $\varphi _0$
satisfying
$\varphi _0$
satisfying
![]() $\varphi _0\circ E_{\lambda }=E_{\tilde {\lambda }}\circ \varphi _1$
and
$\varphi _0\circ E_{\lambda }=E_{\tilde {\lambda }}\circ \varphi _1$
and
![]() $\varphi _1(0)=0$
. We want to see that
$\varphi _1(0)=0$
. We want to see that
![]() $\varphi _0$
is homotopic to
$\varphi _0$
is homotopic to
![]() $\varphi _1$
rel
$\varphi _1$
rel
![]() $P(E_{\lambda })$
. This implies that
$P(E_{\lambda })$
. This implies that
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
are Thurston equivalent, so we have
$E_{\tilde {\lambda }}$
are Thurston equivalent, so we have
![]() $\lambda =\tilde {\lambda }$
by Theorem 6.6 and the remark following it.
$\lambda =\tilde {\lambda }$
by Theorem 6.6 and the remark following it.
Let us first see that
![]() $\varphi _1$
restricts to a conjugation between
$\varphi _1$
restricts to a conjugation between
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
on
$E_{\tilde {\lambda }}$
on
![]() $P(E_{\lambda })$
, just as
$P(E_{\lambda })$
, just as
![]() $\varphi _0$
does. Let
$\varphi _0$
does. Let
![]() $\mathcal {D}$
be the dynamical partition for
$\mathcal {D}$
be the dynamical partition for
![]() $E_{\lambda }$
with respect to g, and let
$E_{\lambda }$
with respect to g, and let
![]() $ \tilde{\mathcal{D}}$
be the dynamical partition for
$ \tilde{\mathcal{D}}$
be the dynamical partition for
![]() $E_{\tilde {\lambda }}$
with respect to
$E_{\tilde {\lambda }}$
with respect to
![]() $\tilde {g}$
. It follows from
$\tilde {g}$
. It follows from
![]() $\varphi _0(\operatorname {\mathrm {Tr}}(g))=\operatorname {\mathrm {Tr}}(\tilde {g})$
and
$\varphi _0(\operatorname {\mathrm {Tr}}(g))=\operatorname {\mathrm {Tr}}(\tilde {g})$
and
![]() $\varphi _1(0)=0$
that the lifted map
$\varphi _1(0)=0$
that the lifted map
![]() $\varphi _1$
maps the partition sector
$\varphi _1$
maps the partition sector
![]() $D_k$
homeomorphically onto the sector
$D_k$
homeomorphically onto the sector
![]() $\tilde {D}_k$
of the same index. Hence, for all
$\tilde {D}_k$
of the same index. Hence, for all
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\varphi _1$
sends the unique pre-image of
$\varphi _1$
sends the unique pre-image of
![]() $E_{\lambda }^{\circ n}(0)$
in the sector
$E_{\lambda }^{\circ n}(0)$
in the sector
![]() $D_k$
to the unique pre-image of
$D_k$
to the unique pre-image of
![]() $E_{\tilde {\lambda }}^{\circ n}(0)$
in
$E_{\tilde {\lambda }}^{\circ n}(0)$
in
![]() $\tilde {D}_k$
. As
$\tilde {D}_k$
. As
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
have the same kneading sequence (remember that the abstract Hubbard tree in particular contains the sector information for the post-singular points), it follows that
$E_{\tilde {\lambda }}$
have the same kneading sequence (remember that the abstract Hubbard tree in particular contains the sector information for the post-singular points), it follows that
![]() $\varphi _1(E_{\lambda }^{\circ (n-1)}(0))=E_{\tilde {\lambda }}^{\circ (n-1)}(0)$
for all
$\varphi _1(E_{\lambda }^{\circ (n-1)}(0))=E_{\tilde {\lambda }}^{\circ (n-1)}(0)$
for all
![]() $n>0$
.
$n>0$
.
Set
![]() $H':=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
and
$H':=[P(E_{\lambda })]_{\widehat {E_{\lambda }}^{-1}(H)}$
and
![]() $\tilde {H}':=[P(E_{\tilde {\lambda }})]_{\widehat {E_{\tilde {\lambda }}}^{-1}(H)}$
. The map
$\tilde {H}':=[P(E_{\tilde {\lambda }})]_{\widehat {E_{\tilde {\lambda }}}^{-1}(H)}$
. The map
![]() $\varphi _1$
extends to a map
$\varphi _1$
extends to a map
![]() $\widehat {\varphi }_1\colon \mathbb {C}_T\to \mathbb {C}_{\tilde {T}}$
by setting
$\widehat {\varphi }_1\colon \mathbb {C}_T\to \mathbb {C}_{\tilde {T}}$
by setting
![]() $\widehat {\varphi }_1(-\infty ):=-\infty $
. As
$\widehat {\varphi }_1(-\infty ):=-\infty $
. As
![]() $\varphi _1(P(E_{\lambda }))=P(E_{\tilde {\lambda }})$
, we have
$\varphi _1(P(E_{\lambda }))=P(E_{\tilde {\lambda }})$
, we have
![]() $\widehat {\varphi }_1(H')=\tilde {H}'$
. By Lemma 3.14, there exists an embedded tree
$\widehat {\varphi }_1(H')=\tilde {H}'$
. By Lemma 3.14, there exists an embedded tree
![]() $H''\subset \mathbb {C}$
such that
$H''\subset \mathbb {C}$
such that
![]() $H''$
is homotopic to
$H''$
is homotopic to
![]() $H'$
rel
$H'$
rel
![]() $P(E_{\lambda })$
. Any homotopy between
$P(E_{\lambda })$
. Any homotopy between
![]() $H'$
and
$H'$
and
![]() $H''$
rel
$H''$
rel
![]() $P(E_{\lambda })$
is pushed forward by
$P(E_{\lambda })$
is pushed forward by
![]() $\varphi _1$
to a homotopy between
$\varphi _1$
to a homotopy between
![]() $\tilde {H}'$
and an embedded tree
$\tilde {H}'$
and an embedded tree
![]() $\tilde {H}'':=\varphi _1(H'')\subset \mathbb {C}$
rel
$\tilde {H}'':=\varphi _1(H'')\subset \mathbb {C}$
rel
![]() $P(E_{\tilde {\lambda }})$
. By Lemma 3.17,
$P(E_{\tilde {\lambda }})$
. By Lemma 3.17,
![]() $H''$
is ambient isotopic to H rel
$H''$
is ambient isotopic to H rel
![]() $P(E_{\lambda })$
and
$P(E_{\lambda })$
and
![]() $\tilde {H}''$
is ambient isotopic to
$\tilde {H}''$
is ambient isotopic to
![]() $\tilde {H}$
rel
$\tilde {H}$
rel
![]() $P(E_{\tilde {\lambda }})$
. Stated differently, there exist homeomorphisms
$P(E_{\tilde {\lambda }})$
. Stated differently, there exist homeomorphisms
![]() $\Psi _0,\Psi _1\colon \mathbb {C}\to \mathbb {C}$
such that
$\Psi _0,\Psi _1\colon \mathbb {C}\to \mathbb {C}$
such that
![]() $\Psi _0$
is isotopic to
$\Psi _0$
is isotopic to
![]() $\text {id}$
rel
$\text {id}$
rel
![]() $P(E_{\lambda })$
,
$P(E_{\lambda })$
,
![]() $\Psi _1$
is isotopic to
$\Psi _1$
is isotopic to
![]() $\text {id}$
rel
$\text {id}$
rel
![]() $P(E_{\tilde {\lambda }})$
, and
$P(E_{\tilde {\lambda }})$
, and
![]() $\varphi _1':=\Psi _1\circ \varphi _1\circ \Psi _0$
satisfies
$\varphi _1':=\Psi _1\circ \varphi _1\circ \Psi _0$
satisfies
![]() $\varphi _1'(H)=\tilde {H}$
. The composition
$\varphi _1'(H)=\tilde {H}$
. The composition
![]() $\varphi _1'$
is isotopic to
$\varphi _1'$
is isotopic to
![]() $\varphi _1$
rel
$\varphi _1$
rel
![]() $P(E_{\lambda })$
and it is equal to
$P(E_{\lambda })$
and it is equal to
![]() $\varphi _0$
on the set of marked points of H. By [Reference Bielefeld, Fisher and HubbardBFH, Corollary 6.3], there exists a homeomorphism
$\varphi _0$
on the set of marked points of H. By [Reference Bielefeld, Fisher and HubbardBFH, Corollary 6.3], there exists a homeomorphism
![]() $\Psi \colon \mathbb {C}\to \mathbb {C}$
isotopic to
$\Psi \colon \mathbb {C}\to \mathbb {C}$
isotopic to
![]() $\text {id}$
relative to the set of marked points of H (and in particular relative to
$\text {id}$
relative to the set of marked points of H (and in particular relative to
![]() $P(E_{\lambda })$
) such that
$P(E_{\lambda })$
) such that
![]() $\varphi _1'\circ \Psi =\varphi _0$
. However,
$\varphi _1'\circ \Psi =\varphi _0$
. However,
![]() $\varphi _1'\circ \Psi $
is isotopic to
$\varphi _1'\circ \Psi $
is isotopic to
![]() $\varphi _1$
rel
$\varphi _1$
rel
![]() $P(E_{\lambda })$
, so
$P(E_{\lambda })$
, so
![]() $E_{\lambda }$
and
$E_{\lambda }$
and
![]() $E_{\tilde {\lambda }}$
are Thurston equivalent.
$E_{\tilde {\lambda }}$
are Thurston equivalent.
Next, we explain how to obtain a topological exponential map from an abstract exponential Hubbard tree. For convenience, we are going to embed abstract Hubbard trees into the complex plane
![]() $\mathbb {C}$
(or suitable extensions of it). Note, however, that the complex structure of
$\mathbb {C}$
(or suitable extensions of it). Note, however, that the complex structure of
![]() $\mathbb {C}$
does not play any role; it only simplifies the construction. At first, we define a suitable embedding of the abstract tree into the complex plane. Afterwards, we show that the self-map of the embedded tree extends to a map on the plane and that this map is a topological exponential map. The constructions are inspired by and similar to those in [Reference Laubner, Schleicher and VicolLSV, Ch. 5], so we skim some of them and refer to [Reference Laubner, Schleicher and VicolLSV] for more details.
$\mathbb {C}$
does not play any role; it only simplifies the construction. At first, we define a suitable embedding of the abstract tree into the complex plane. Afterwards, we show that the self-map of the embedded tree extends to a map on the plane and that this map is a topological exponential map. The constructions are inspired by and similar to those in [Reference Laubner, Schleicher and VicolLSV, Ch. 5], so we skim some of them and refer to [Reference Laubner, Schleicher and VicolLSV] for more details.
At first, we specify a general mapping layout for all of our topological exponential maps, which is independent of the abstract Hubbard tree that we want to realize. See Figure 4 for a sketch of the upcoming construction. Let
![]() $\gamma _h\colon (0,\infty )\to \mathbb {C}$
,
$\gamma _h\colon (0,\infty )\to \mathbb {C}$
,
![]() $\gamma _h(t):=t$
be a parameterization of the horizontal line of positive reals. For each
$\gamma _h(t):=t$
be a parameterization of the horizontal line of positive reals. For each
![]() $k\in \mathbb {Z}$
, let
$k\in \mathbb {Z}$
, let
![]() $d_k\colon (-\infty ,+\infty )\to \mathbb {C}$
, and
$d_k\colon (-\infty ,+\infty )\to \mathbb {C}$
, and
![]() $d_k(t):= t+(2k-1)\pi i$
be a parameterization of the straight horizontal line at constant imaginary part
$d_k(t):= t+(2k-1)\pi i$
be a parameterization of the straight horizontal line at constant imaginary part
![]() $(2k-1)\pi $
. We define a continuous map
$(2k-1)\pi $
. We define a continuous map
![]() $g_0\colon \bigcup \operatorname {\mathrm {Tr}}(d_k)\to \operatorname {\mathrm {Tr}}(\gamma _h)$
by
$g_0\colon \bigcup \operatorname {\mathrm {Tr}}(d_k)\to \operatorname {\mathrm {Tr}}(\gamma _h)$
by
![]() $g_0(d_k(t)):=\gamma _h(\exp (t))$
. Denote by
$g_0(d_k(t)):=\gamma _h(\exp (t))$
. Denote by
![]() $D_j$
the connected component of
$D_j$
the connected component of
![]() $\mathbb {C}\setminus \bigcup \operatorname {\mathrm {Tr}}(d_k)$
bounded by
$\mathbb {C}\setminus \bigcup \operatorname {\mathrm {Tr}}(d_k)$
bounded by
![]() $\operatorname {\mathrm {Tr}}(d_j)$
and
$\operatorname {\mathrm {Tr}}(d_j)$
and
![]() $\operatorname {\mathrm {Tr}}(d_{j+1})$
.
$\operatorname {\mathrm {Tr}}(d_{j+1})$
.

Figure 4 Sketch of the embedded trees
![]() $H:=\iota (\mathtt {H})$
and
$H:=\iota (\mathtt {H})$
and
![]() $H':=\iota {(\mathtt {H})}$
. The two embedded trees agree on
$H':=\iota {(\mathtt {H})}$
. The two embedded trees agree on
![]() $\{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)\geq -1\}$
.
$\{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)\geq -1\}$
.
Let
![]() $\mathtt {(H,f,B_{k_i},\angle _v)}$
(we use a different font here to distinguish the abstract tree from the embedded tree) be an abstract Hubbard tree. The branches
$\mathtt {(H,f,B_{k_i},\angle _v)}$
(we use a different font here to distinguish the abstract tree from the embedded tree) be an abstract Hubbard tree. The branches
![]() $\mathtt {B_{k_0}, \ldots , B_{k_n}}$
of
$\mathtt {B_{k_0}, \ldots , B_{k_n}}$
of
![]() $\mathtt {H}$
at
$\mathtt {H}$
at
![]() $\mathtt {v_T}$
are indexed by distinct integers
$\mathtt {v_T}$
are indexed by distinct integers
![]() $\mathtt {k_i\in \mathbb {Z}}$
, where
$\mathtt {k_i\in \mathbb {Z}}$
, where
![]() $\mathtt {k_0}=0$
(compare Definition 4.2). Denote by
$\mathtt {k_0}=0$
(compare Definition 4.2). Denote by
![]() $\mathtt {v_{k_i}^{(1)},\ldots , v_{k_i}^{(j_{k_i})}\in V_f\cap B_{k_i}}$
the marked points of
$\mathtt {v_{k_i}^{(1)},\ldots , v_{k_i}^{(j_{k_i})}\in V_f\cap B_{k_i}}$
the marked points of
![]() $\mathtt {(H,f,B_{k_i},\angle _v)}$
contained in the branch
$\mathtt {(H,f,B_{k_i},\angle _v)}$
contained in the branch
![]() $\mathtt {B_{k_i}}$
, where
$\mathtt {B_{k_i}}$
, where
![]() $\mathtt {v_{k_i}^{(1)}}$
is the unique marked point in
$\mathtt {v_{k_i}^{(1)}}$
is the unique marked point in
![]() $\mathtt {B_{k_i}}$
incident to
$\mathtt {B_{k_i}}$
incident to
![]() $\mathtt {v_T}$
. Choose auxiliary points
$\mathtt {v_T}$
. Choose auxiliary points
![]() $\mathtt {v_{k_i}^{(0)}\in (v_T,v_{k_i}^{(1)})}$
. We define an embedding
$\mathtt {v_{k_i}^{(0)}\in (v_T,v_{k_i}^{(1)})}$
. We define an embedding
![]() $\iota \colon \mathtt {H}\to \mathbb {C}$
in the following way.
$\iota \colon \mathtt {H}\to \mathbb {C}$
in the following way.
-
• For
 $i\in \{0,\ldots , n\}$
, set
$i\in \{0,\ldots , n\}$
, set
 $\iota (\mathtt {v_{k_i}^{(0)}}):= -1 + 2k_i\pi i=:v_{k_i}^{(0)}$
.
$\iota (\mathtt {v_{k_i}^{(0)}}):= -1 + 2k_i\pi i=:v_{k_i}^{(0)}$
. -
• Choose an arbitrary point
 $v_T\in \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)<-1\}$
and choose pairwise disjoint arcs
$v_T\in \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)<-1\}$
and choose pairwise disjoint arcs
 $\gamma _i\colon [0,1]\to \mathbb {C}$
connecting
$\gamma _i\colon [0,1]\to \mathbb {C}$
connecting
 $v_T$
to
$v_T$
to
 $v_{k_i}^{(0)}$
such that
$v_{k_i}^{(0)}$
such that
 $\gamma _i((0,1))\subset \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)<-1\}$
. Let
$\gamma _i((0,1))\subset \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)<-1\}$
. Let
 $\iota \colon [\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]\to \operatorname {\mathrm {Tr}}(\gamma _i)$
to be a homeomorphism satisfying
$\iota \colon [\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]\to \operatorname {\mathrm {Tr}}(\gamma _i)$
to be a homeomorphism satisfying
 $\iota (\mathtt {v_T})=v_T$
and
$\iota (\mathtt {v_T})=v_T$
and
 $\iota (\mathtt {v_{k_i}^{(0)}})=v_{k_i}^{(0)}$
.
$\iota (\mathtt {v_{k_i}^{(0)}})=v_{k_i}^{(0)}$
. -
• For
 $i\in \{1,\ldots , n\}$
, choose distinct points
$i\in \{1,\ldots , n\}$
, choose distinct points
 $v_{k_i}^{(1)},\ldots , v_{k_i}^{(j_{k_i})}\in D_{k_i}$
satisfying
$v_{k_i}^{(1)},\ldots , v_{k_i}^{(j_{k_i})}\in D_{k_i}$
satisfying
 $\operatorname {Re}(v_{k_i}^{(j)})>-1$
. Define
$\operatorname {Re}(v_{k_i}^{(j)})>-1$
. Define
 $\iota \colon {\mathtt {B_{k_i}\setminus [v_T,v_{k_i}^{(0)}]}}\to D_{k_i}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)>-1\}$
to be an embedding satisfying
$\iota \colon {\mathtt {B_{k_i}\setminus [v_T,v_{k_i}^{(0)}]}}\to D_{k_i}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)>-1\}$
to be an embedding satisfying
 $\iota (\mathtt {v_{k_i}^{(j)}})=v_{k_i}^{(j)}$
such that the cyclic order of branches at
$\iota (\mathtt {v_{k_i}^{(j)}})=v_{k_i}^{(j)}$
such that the cyclic order of branches at
 $v_{k_i}^{(j)}$
coincides with the cyclic order of the corresponding branches of the abstract tree at
$v_{k_i}^{(j)}$
coincides with the cyclic order of the corresponding branches of the abstract tree at
 $\mathtt {v_{k_i}^{(j)}}$
. For the embedding of
$\mathtt {v_{k_i}^{(j)}}$
. For the embedding of
 $\mathtt {B_0}$
, we require
$\mathtt {B_0}$
, we require
 $\iota (\mathtt {f(v_T)})=0$
and
$\iota (\mathtt {f(v_T)})=0$
and
 $\iota (\mathtt {B_0})\cap \operatorname {\mathrm {Tr}}(\gamma _h)=\emptyset $
in addition. Note that every oriented topological tree is planar, so there always exists such an embedding.
$\iota (\mathtt {B_0})\cap \operatorname {\mathrm {Tr}}(\gamma _h)=\emptyset $
in addition. Note that every oriented topological tree is planar, so there always exists such an embedding.
The image
![]() $H:=\iota (\mathtt {H})\subset \mathbb {C}$
is an embedded tree. Next, we define a slightly different embedding
$H:=\iota (\mathtt {H})\subset \mathbb {C}$
is an embedded tree. Next, we define a slightly different embedding
![]() $\iota '$
of
$\iota '$
of
![]() $\mathtt {H}$
whose image will be the subset
$\mathtt {H}$
whose image will be the subset
![]() $H'$
of the pre-image tree of H spanned by
$H'$
of the pre-image tree of H spanned by
![]() $P(g)$
under the yet to be constructed topological exponential map g.
$P(g)$
under the yet to be constructed topological exponential map g.
Let
![]() $-\infty $
and
$-\infty $
and
![]() $+\infty $
be abstract points not contained in
$+\infty $
be abstract points not contained in
![]() $\mathbb {C}$
and let
$\mathbb {C}$
and let
![]() $C_{\infty }:=\mathbb {C}\cup \{-\infty ,+\infty \}$
denote the extension of the complex plane by these abstract points. We turn
$C_{\infty }:=\mathbb {C}\cup \{-\infty ,+\infty \}$
denote the extension of the complex plane by these abstract points. We turn
![]() $\mathbb {C}_{\infty }$
into a topological space by defining
$\mathbb {C}_{\infty }$
into a topological space by defining
![]() $U_n:=\{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)<-n\}\cup \{-\infty \}$
to be a neighborhood basis of
$U_n:=\{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)<-n\}\cup \{-\infty \}$
to be a neighborhood basis of
![]() $-\infty $
and
$-\infty $
and
![]() $V_n:=\{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)>n\}\cup \{+\infty \}$
to be a neighborhood basis of
$V_n:=\{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)>n\}\cup \{+\infty \}$
to be a neighborhood basis of
![]() $+\infty $
. For every
$+\infty $
. For every
![]() $i\in \{0,\ldots , n\}$
, let
$i\in \{0,\ldots , n\}$
, let
![]() $\tilde {\gamma }_i\colon [0,1]\to \mathbb {C}_{\infty }$
be an arc connecting
$\tilde {\gamma }_i\colon [0,1]\to \mathbb {C}_{\infty }$
be an arc connecting
![]() $-\infty $
to
$-\infty $
to
![]() $v_{k_i}^{(0)}$
and satisfying
$v_{k_i}^{(0)}$
and satisfying
![]() $\gamma _i((0,1))\subset D_{k_i}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)< -1\}$
. Let
$\gamma _i((0,1))\subset D_{k_i}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Re}(z)< -1\}$
. Let
![]() $\iota '|_{[\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]}\colon [\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]\to \operatorname {\mathrm {Tr}}(\tilde {\gamma }_i)$
be a homeomorphism, where
$\iota '|_{[\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]}\colon [\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]\to \operatorname {\mathrm {Tr}}(\tilde {\gamma }_i)$
be a homeomorphism, where
![]() $\iota '(\mathtt {v_T})=-\infty $
and
$\iota '(\mathtt {v_T})=-\infty $
and
![]() $\iota '(\mathtt {v_{k_i}^{(0)}})=v_{k_i}^{(0)}$
. On the complement of
$\iota '(\mathtt {v_{k_i}^{(0)}})=v_{k_i}^{(0)}$
. On the complement of
![]() $[\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]$
, define
$[\mathtt {v_T},\mathtt {v_{k_i}^{(0)}}]$
, define
![]() $\iota '$
to be equal to
$\iota '$
to be equal to
![]() $\iota $
and set
$\iota $
and set
![]() $H':=\iota '(\mathtt {H})\subset \mathbb {C}_{\infty }$
.
$H':=\iota '(\mathtt {H})\subset \mathbb {C}_{\infty }$
.
The next step is to define a map from
![]() $H'$
to H. From now on, let
$H'$
to H. From now on, let
![]() $d_i\colon [-\infty ,+\infty ]\to \mathbb {C}_{\infty }$
denote the extended curve, where
$d_i\colon [-\infty ,+\infty ]\to \mathbb {C}_{\infty }$
denote the extended curve, where
![]() $d_i(-\infty )=-\infty $
and
$d_i(-\infty )=-\infty $
and
![]() $d_i(+\infty )=+\infty $
. We also extend
$d_i(+\infty )=+\infty $
. We also extend
![]() $\gamma _h$
to a curve
$\gamma _h$
to a curve
![]() $\gamma _h\colon [0,+\infty ]\to \overline {\mathbb {C}}$
, where
$\gamma _h\colon [0,+\infty ]\to \overline {\mathbb {C}}$
, where
![]() $\gamma _h(0)=0$
and
$\gamma _h(0)=0$
and
![]() $\gamma _h(+\infty )=\infty $
. Then we define an extended map
$\gamma _h(+\infty )=\infty $
. Then we define an extended map
![]() $g_0\colon \bigcup \operatorname {\mathrm {Tr}}(d_i)\to \operatorname {\mathrm {Tr}}(\gamma )$
by setting
$g_0\colon \bigcup \operatorname {\mathrm {Tr}}(d_i)\to \operatorname {\mathrm {Tr}}(\gamma )$
by setting
![]() $g_0(-\infty )=0$
and
$g_0(-\infty )=0$
and
![]() $g_0(+\infty )=\infty $
. We define a graph map
$g_0(+\infty )=\infty $
. We define a graph map
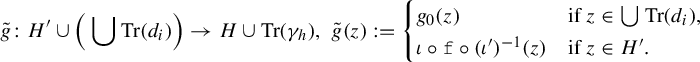 $$ \begin{align*} \tilde{g}\colon H'\cup\Big(\bigcup\operatorname{\mathrm{Tr}}(d_i)\Big)\to H\cup\operatorname{\mathrm{Tr}}(\gamma_h),~\tilde{g}(z):= \begin{cases} g_0(z) & \text{if}~z\in\bigcup\operatorname{\mathrm{Tr}}(d_i),\\ \iota\circ \mathtt{f}\circ(\iota')^{-1}(z) & \text{if}~z\in H'. \end{cases} \end{align*} $$
$$ \begin{align*} \tilde{g}\colon H'\cup\Big(\bigcup\operatorname{\mathrm{Tr}}(d_i)\Big)\to H\cup\operatorname{\mathrm{Tr}}(\gamma_h),~\tilde{g}(z):= \begin{cases} g_0(z) & \text{if}~z\in\bigcup\operatorname{\mathrm{Tr}}(d_i),\\ \iota\circ \mathtt{f}\circ(\iota')^{-1}(z) & \text{if}~z\in H'. \end{cases} \end{align*} $$
Our next goal is to show that the graph map
![]() $\tilde {g}$
can be extended to a post-singularly finite topological exponential map. Let us see how to use Lemma 6.8 in our setting. There exist continuous maps
$\tilde {g}$
can be extended to a post-singularly finite topological exponential map. Let us see how to use Lemma 6.8 in our setting. There exist continuous maps
![]() $\varphi _1\colon \overline {\mathbb {D}}\to \text {cl}_{\mathbb {C}_{\infty }}(D_i)$
and
$\varphi _1\colon \overline {\mathbb {D}}\to \text {cl}_{\mathbb {C}_{\infty }}(D_i)$
and
![]() $\varphi _2\colon \overline {\mathbb {D}}\to \text {cl}_{\overline {\mathbb {C}}}(\mathbb {C}\setminus \operatorname {\mathrm {Tr}}(\gamma _h))$
that restrict to orientation-preserving homeomorphisms from
$\varphi _2\colon \overline {\mathbb {D}}\to \text {cl}_{\overline {\mathbb {C}}}(\mathbb {C}\setminus \operatorname {\mathrm {Tr}}(\gamma _h))$
that restrict to orientation-preserving homeomorphisms from
![]() $\mathbb {D}$
onto
$\mathbb {D}$
onto
![]() $D_i$
and
$D_i$
and
![]() $\mathbb {C}\setminus \operatorname {\mathrm {Tr}}(\gamma _h)$
, respectively. The map
$\mathbb {C}\setminus \operatorname {\mathrm {Tr}}(\gamma _h)$
, respectively. The map
![]() $\varphi _1$
is a homeomorphism, while every interior point of
$\varphi _1$
is a homeomorphism, while every interior point of
![]() $\operatorname {\mathrm {Tr}}(\gamma _h)$
has two pre-images under
$\operatorname {\mathrm {Tr}}(\gamma _h)$
has two pre-images under
![]() $\varphi _2$
. We choose
$\varphi _2$
. We choose
![]() $\varphi _1$
to satisfy
$\varphi _1$
to satisfy
![]() $\varphi _1(1)=+\infty $
,
$\varphi _1(1)=+\infty $
,
![]() $\varphi _1(-1)=-\infty $
, and
$\varphi _1(-1)=-\infty $
, and
![]() $\varphi _2$
to satisfy
$\varphi _2$
to satisfy
![]() $\varphi _2(-1)=0$
,
$\varphi _2(-1)=0$
,
![]() $\varphi _2(1)=\infty $
. Then, there exist inverse branches
$\varphi _2(1)=\infty $
. Then, there exist inverse branches
![]() $\psi _u\colon \operatorname {\mathrm {Tr}}(\gamma _h)\to \partial \mathbb {D}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Im}(z)\geq 0\}$
and
$\psi _u\colon \operatorname {\mathrm {Tr}}(\gamma _h)\to \partial \mathbb {D}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Im}(z)\geq 0\}$
and
![]() $\psi _l\colon \operatorname {\mathrm {Tr}}(\gamma _h)\to \partial \mathbb {D}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Im}(z)\leq 0\}$
of
$\psi _l\colon \operatorname {\mathrm {Tr}}(\gamma _h)\to \partial \mathbb {D}\cap \{z\in \mathbb {C}~\vert ~\operatorname {Im}(z)\leq 0\}$
of
![]() $\varphi _2$
. We define a homeomorphism
$\varphi _2$
. We define a homeomorphism
![]() $f\colon \partial \mathbb {D}\to \partial \mathbb {D}$
by
$f\colon \partial \mathbb {D}\to \partial \mathbb {D}$
by
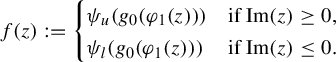 $$ \begin{align*} f(z):=\begin{cases} \psi_u(g_0(\varphi_1(z))) & \text{if} \operatorname{Im}(z)\geq 0, \\ \psi_l(g_0(\varphi_1(z))) & \text{if} \operatorname{Im}(z)\leq 0. \end{cases} \end{align*} $$
$$ \begin{align*} f(z):=\begin{cases} \psi_u(g_0(\varphi_1(z))) & \text{if} \operatorname{Im}(z)\geq 0, \\ \psi_l(g_0(\varphi_1(z))) & \text{if} \operatorname{Im}(z)\leq 0. \end{cases} \end{align*} $$
We view
![]() $\overline {\mathbb {D}}\subset \overline {\mathbb {C}}$
as a subset of the Riemann sphere. Setting
$\overline {\mathbb {D}}\subset \overline {\mathbb {C}}$
as a subset of the Riemann sphere. Setting
![]() $\Gamma _1:=\varphi _1^{-1}(\partial D_i\cup (H'\cap D_i))$
,
$\Gamma _1:=\varphi _1^{-1}(\partial D_i\cup (H'\cap D_i))$
,
![]() $\Gamma _2:=\varphi _2^{-1}(\tilde {g}(H'\cap D_i)\cup \operatorname {\mathrm {Tr}}(\gamma _h))$
, the
$\Gamma _2:=\varphi _2^{-1}(\tilde {g}(H'\cap D_i)\cup \operatorname {\mathrm {Tr}}(\gamma _h))$
, the
![]() $\Gamma _i\subset \overline {\mathbb {C}}$
are connected embedded graphs. We extend f to a homeomorphism
$\Gamma _i\subset \overline {\mathbb {C}}$
are connected embedded graphs. We extend f to a homeomorphism
![]() $f\colon \Gamma _1\to \Gamma _2$
by setting
$f\colon \Gamma _1\to \Gamma _2$
by setting
![]() $f(z)=\varphi _2^{-1}(\tilde {g}(\varphi _1(z)))$
for
$f(z)=\varphi _2^{-1}(\tilde {g}(\varphi _1(z)))$
for
![]() $z\in \Gamma _1\setminus \partial \mathbb {D}$
. Then f preserves the circular order at branch points of
$z\in \Gamma _1\setminus \partial \mathbb {D}$
. Then f preserves the circular order at branch points of
![]() $\Gamma _1$
because
$\Gamma _1$
because
![]() $\tilde {g}$
preserves the circular order at branch points. By Lemma 6.8, there exists an orientation-preserving homeomorphism
$\tilde {g}$
preserves the circular order at branch points. By Lemma 6.8, there exists an orientation-preserving homeomorphism
![]() $\hat {f}\colon \overline {\mathbb {C}}\to \overline {\mathbb {C}}$
extending f and satisfying
$\hat {f}\colon \overline {\mathbb {C}}\to \overline {\mathbb {C}}$
extending f and satisfying
![]() $\hat {f}(\overline {\mathbb {D}})=\overline {\mathbb {D}}$
. We define
$\hat {f}(\overline {\mathbb {D}})=\overline {\mathbb {D}}$
. We define
![]() $g(z):=\varphi _2\circ \hat {f}\circ \varphi _1^{-1}$
for
$g(z):=\varphi _2\circ \hat {f}\circ \varphi _1^{-1}$
for
![]() $z\in D_i$
.
$z\in D_i$
.
Pasting these extensions together, we obtain a globally defined map
![]() $g\colon \mathbb {C}\to \mathbb {C}\setminus \{0\}$
. As it is a covering map, it is a post-singularly finite topological exponential map. To see that g is Thurston equivalent to a holomorphic map, we have to show that g does not admit a Levy cycle. We can assume without loss of generality that
$g\colon \mathbb {C}\to \mathbb {C}\setminus \{0\}$
. As it is a covering map, it is a post-singularly finite topological exponential map. To see that g is Thurston equivalent to a holomorphic map, we have to show that g does not admit a Levy cycle. We can assume without loss of generality that
![]() $\gamma _h$
is pre-periodic (as a set) under the dynamics of g and the forward images of
$\gamma _h$
is pre-periodic (as a set) under the dynamics of g and the forward images of
![]() $\gamma _h$
are pairwise disjoint (except possibly for their landing points). By construction, the boundary of the partition
$\gamma _h$
are pairwise disjoint (except possibly for their landing points). By construction, the boundary of the partition
![]() $(D_j)_{j\in \mathbb {Z}}$
consists of the pre-images of
$(D_j)_{j\in \mathbb {Z}}$
consists of the pre-images of
![]() $\gamma _h$
, and by expansivity of the abstract Hubbard Tree, different post-singular points have different itineraries with respect to
$\gamma _h$
, and by expansivity of the abstract Hubbard Tree, different post-singular points have different itineraries with respect to
![]() $(D_j)_{j\in \mathbb {Z}}$
.
$(D_j)_{j\in \mathbb {Z}}$
.
Lemma 6.10. The map g does not admit a Levy cycle.
Proof Assume to the contrary that g admits a Levy cycle
![]() $\Lambda =\{\delta _0,\delta _1,\ldots , \delta _k=\delta _0\}$
. Set
$\Lambda =\{\delta _0,\delta _1,\ldots , \delta _k=\delta _0\}$
. Set
![]() $\gamma _0:=\gamma _h$
and denote by
$\gamma _0:=\gamma _h$
and denote by
![]() $\gamma _i:=g^{\circ i}(\gamma _0)$
the forward iterates of
$\gamma _i:=g^{\circ i}(\gamma _0)$
the forward iterates of
![]() $\gamma _0$
. By construction,
$\gamma _0$
. By construction,
![]() $\gamma _0$
is pre-periodic as a set. For curves
$\gamma _0$
is pre-periodic as a set. For curves
![]() $\delta _j$
and
$\delta _j$
and
![]() $\gamma _i$
, let
$\gamma _i$
, let
denote the minimal intersection number of
![]() $\delta _j$
and
$\delta _j$
and
![]() $\gamma _i$
. It follows from the periodicity of the curves
$\gamma _i$
. It follows from the periodicity of the curves
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\delta _j$
that
$\delta _j$
that
![]() $\vert [\delta _j]\cap [\gamma _0]\vert =0$
for all
$\vert [\delta _j]\cap [\gamma _0]\vert =0$
for all
![]() $j\in \{0,\ldots , k-1\}$
. See [Reference Bielefeld, Fisher and HubbardBFH, Lemma 8.7] for a proof of this fact. Therefore, the curves
$j\in \{0,\ldots , k-1\}$
. See [Reference Bielefeld, Fisher and HubbardBFH, Lemma 8.7] for a proof of this fact. Therefore, the curves
![]() $\delta _j$
of the Levy cycle do not intersect the partition boundary (up to homotopy), so all post-singular points surrounded by the same curve
$\delta _j$
of the Levy cycle do not intersect the partition boundary (up to homotopy), so all post-singular points surrounded by the same curve
![]() $\delta _j$
have equal itineraries. This contradicts the fact that different post-singular points have different itineraries with respect to
$\delta _j$
have equal itineraries. This contradicts the fact that different post-singular points have different itineraries with respect to
![]() $(D_j)_{j\in \mathbb {Z}}$
. See [Reference Laubner, Schleicher and VicolLSV, Lemma 5.5] for a detailed proof.
$(D_j)_{j\in \mathbb {Z}}$
. See [Reference Laubner, Schleicher and VicolLSV, Lemma 5.5] for a detailed proof.
By Theorem 6.6 and Lemma 6.10, the topological exponential map g is Thurston equivalent to a holomorphic exponential map
![]() $E_{\lambda _g}$
. We are in the position to close the classification cycle.
$E_{\lambda _g}$
. We are in the position to close the classification cycle.
Theorem 6.11. (Classification of post-singularly finite exponential maps by abstract Hubbard trees)
The map
is a bijection between post-singularly finite exponential maps (up to affine conjugation) and abstract exponential Hubbard trees (up to equivalence).
Proof We have already shown that
![]() $\mathcal {F}$
is well defined. We choose a representative for every equivalence class of abstract exponential Hubbard trees and perform the construction above to obtain a post-singularly finite exponential map associated with it. This sets up a map
$\mathcal {F}$
is well defined. We choose a representative for every equivalence class of abstract exponential Hubbard trees and perform the construction above to obtain a post-singularly finite exponential map associated with it. This sets up a map
Let
![]() $\mathtt {(H,f,B_{k_i},\angle _v)}$
be the chosen representative for a given equivalence class of abstract Hubbard trees and let
$\mathtt {(H,f,B_{k_i},\angle _v)}$
be the chosen representative for a given equivalence class of abstract Hubbard trees and let
![]() $E_{\lambda _g}=\mathcal {G}([\mathtt {(H,f,B_{k_i},\angle _v)}])$
be the corresponding holomorphic exponential map obtained by the construction above. We want to see that
$E_{\lambda _g}=\mathcal {G}([\mathtt {(H,f,B_{k_i},\angle _v)}])$
be the corresponding holomorphic exponential map obtained by the construction above. We want to see that
![]() $\mathcal {F}(E_{\lambda _g})=[\mathtt {(H,f,B_{k_i},\angle _v)}]$
, that is,
$\mathcal {F}(E_{\lambda _g})=[\mathtt {(H,f,B_{k_i},\angle _v)}]$
, that is,
![]() $\mathcal {F}\circ \mathcal {G}=\text {id}$
. As we have already seen in Theorem 6.9 that
$\mathcal {F}\circ \mathcal {G}=\text {id}$
. As we have already seen in Theorem 6.9 that
![]() $\mathcal {F}$
is injective, this shows that
$\mathcal {F}$
is injective, this shows that
![]() $\mathcal {F}$
is indeed a bijection.
$\mathcal {F}$
is indeed a bijection.
By the definition of Thurston equivalence, there exist two homeomorphisms
![]() $\varphi _0,\varphi _1\colon \mathbb {C}\to \mathbb {C}$
such that the diagram
$\varphi _0,\varphi _1\colon \mathbb {C}\to \mathbb {C}$
such that the diagram

commutes and
![]() $\varphi _0$
and
$\varphi _0$
and
![]() $\varphi _1$
are homotopic rel
$\varphi _1$
are homotopic rel
![]() $P(g)$
. We want to see that
$P(g)$
. We want to see that
![]() $H_0:=\varphi _0(H)$
is a homotopy Hubbard tree for
$H_0:=\varphi _0(H)$
is a homotopy Hubbard tree for
![]() $E_{\lambda _g}$
and that it yields the abstract exponential Hubbard tree with which we have started. Obviously,
$E_{\lambda _g}$
and that it yields the abstract exponential Hubbard tree with which we have started. Obviously,
![]() $H_0$
is a finite embedded tree spanned by
$H_0$
is a finite embedded tree spanned by
![]() $P(E_{\lambda _g})$
. We want to see that
$P(E_{\lambda _g})$
. We want to see that
![]() $H_0$
is invariant up to homotopy rel
$H_0$
is invariant up to homotopy rel
![]() $P(E_{\lambda _g})$
. Set
$P(E_{\lambda _g})$
. Set
![]() $H_1:=\varphi _1(H)$
. By Proposition 3.12,
$H_1:=\varphi _1(H)$
. By Proposition 3.12,
![]() $\varphi _0$
and
$\varphi _0$
and
![]() $\varphi _1$
are isotopic rel
$\varphi _1$
are isotopic rel
![]() $P(g)$
, and hence the embedded trees
$P(g)$
, and hence the embedded trees
![]() $H_0$
and
$H_0$
and
![]() $H_1$
are ambient isotopic. More precisely, the map
$H_1$
are ambient isotopic. More precisely, the map
![]() $\varphi :=\varphi _1\circ \varphi _0^{-1}\colon \mathbb {C}\to \mathbb {C}$
is isotopic to
$\varphi :=\varphi _1\circ \varphi _0^{-1}\colon \mathbb {C}\to \mathbb {C}$
is isotopic to
![]() $\text {id}$
rel
$\text {id}$
rel
![]() $P(E_{\lambda _g})$
such that
$P(E_{\lambda _g})$
such that
![]() $\varphi (H_0)=H_1$
. We want to see that
$\varphi (H_0)=H_1$
. We want to see that
![]() $H_0'=[P(E_{\lambda _g})]_{\widehat {E_{\lambda _g}}^{-1}(H_0)}$
is homotopic to
$H_0'=[P(E_{\lambda _g})]_{\widehat {E_{\lambda _g}}^{-1}(H_0)}$
is homotopic to
![]() $H_0$
in
$H_0$
in
![]() $\mathbb {C}_T$
rel
$\mathbb {C}_T$
rel
![]() $P(E_{\lambda _g})$
.
$P(E_{\lambda _g})$
.
By construction, there exists a homotopy
![]() $I\colon H\times [0,1]\to \mathbb {C}\cup \{-\infty \}$
between H and
$I\colon H\times [0,1]\to \mathbb {C}\cup \{-\infty \}$
between H and
![]() $H'$
rel
$H'$
rel
![]() $P(g)$
satisfying
$P(g)$
satisfying
![]() $I^1=\iota '\circ \iota ^{-1}$
. The homeomorphism
$I^1=\iota '\circ \iota ^{-1}$
. The homeomorphism
![]() $\varphi _1$
extends to a homeomorphism
$\varphi _1$
extends to a homeomorphism
![]() $\widehat {\varphi _1}\colon \mathbb {C}\cup \{-\infty \}\to \mathbb {C}_T$
by setting
$\widehat {\varphi _1}\colon \mathbb {C}\cup \{-\infty \}\to \mathbb {C}_T$
by setting
![]() $\widehat {\varphi _1}(-\infty ):=-\infty $
. By commutativity of the Thurston diagram, we have
$\widehat {\varphi _1}(-\infty ):=-\infty $
. By commutativity of the Thurston diagram, we have
![]() $H_0'=\widehat {\varphi _1}(H')$
. The homotopy I is pushed forward through
$H_0'=\widehat {\varphi _1}(H')$
. The homotopy I is pushed forward through
![]() $\widehat {\varphi _1}$
to a homotopy
$\widehat {\varphi _1}$
to a homotopy
![]() $\tilde {I}:=\widehat {\varphi _1}\circ I$
between
$\tilde {I}:=\widehat {\varphi _1}\circ I$
between
![]() $H_1$
and
$H_1$
and
![]() $H_0'$
rel
$H_0'$
rel
![]() $P(E_{\lambda _g})$
. We have shown above that
$P(E_{\lambda _g})$
. We have shown above that
![]() $H_1$
is homotopic to
$H_1$
is homotopic to
![]() $H_0$
rel
$H_0$
rel
![]() $P(E_{\lambda _g})$
, so
$P(E_{\lambda _g})$
, so
![]() $H_0$
is homotopic to
$H_0$
is homotopic to
![]() $H_0'$
rel
$H_0'$
rel
![]() $P(E_{\lambda _g})$
.
$P(E_{\lambda _g})$
.
The identification of
![]() $H_0$
with
$H_0$
with
![]() $H_0'$
yielded by the constructed homotopy is given by
$H_0'$
yielded by the constructed homotopy is given by
![]() $\psi :=\widehat {\varphi _1}\circ \iota '\circ \iota ^{-1}\circ \varphi _0^{-1}\colon H_0\to H_0'$
. It remains to show that the induced self-map
$\psi :=\widehat {\varphi _1}\circ \iota '\circ \iota ^{-1}\circ \varphi _0^{-1}\colon H_0\to H_0'$
. It remains to show that the induced self-map
![]() $f:=E_{\lambda _g}\circ \tilde {\psi }\colon H_0\to H_0$
is expansive. Looking carefully at the definition of the involved maps, we see that
$f:=E_{\lambda _g}\circ \tilde {\psi }\colon H_0\to H_0$
is expansive. Looking carefully at the definition of the involved maps, we see that
![]() $f=(\varphi _0\circ \iota )\circ \mathtt {f}\circ (\varphi _0\circ \iota )^{-1}$
, that is, the self-map of
$f=(\varphi _0\circ \iota )\circ \mathtt {f}\circ (\varphi _0\circ \iota )^{-1}$
, that is, the self-map of
![]() $H_0$
is conjugate to the self-map
$H_0$
is conjugate to the self-map
![]() $\mathtt {f}$
of the abstract Hubbard tree
$\mathtt {f}$
of the abstract Hubbard tree
![]() $\mathtt {H}$
. Hence, f is expansive by the expansivity of
$\mathtt {H}$
. Hence, f is expansive by the expansivity of
![]() $\mathtt {f}$
.
$\mathtt {f}$
.
This also shows that the abstract Hubbard trees
![]() $(H_0,f,B_{k_i},\angle _v)$
and
$(H_0,f,B_{k_i},\angle _v)$
and
![]() $\mathtt {(H,f,B_{k_i},\angle _v)}$
are equivalent through
$\mathtt {(H,f,B_{k_i},\angle _v)}$
are equivalent through
![]() $\varphi _0\circ \iota $
except for the fact that the sector information of
$\varphi _0\circ \iota $
except for the fact that the sector information of
![]() $\mathtt {H}$
and
$\mathtt {H}$
and
![]() $H_0$
is consistent. For a post-singular point
$H_0$
is consistent. For a post-singular point
![]() $\mathtt {p\in B_{k_i}}$
, we have
$\mathtt {p\in B_{k_i}}$
, we have
![]() $\iota (\mathtt {p})\in D_{k_i}$
, where
$\iota (\mathtt {p})\in D_{k_i}$
, where
![]() $(D_i)_{i\in \mathbb {Z}}$
is the partition for g defined above. As
$(D_i)_{i\in \mathbb {Z}}$
is the partition for g defined above. As
![]() $\operatorname {\mathrm {Tr}}(\gamma _h)\cap H=\{0\}$
, we have
$\operatorname {\mathrm {Tr}}(\gamma _h)\cap H=\{0\}$
, we have
![]() $H_0\cap \operatorname {\mathrm {Tr}}(\gamma )=\{0\}$
, where
$H_0\cap \operatorname {\mathrm {Tr}}(\gamma )=\{0\}$
, where
![]() $\gamma :=\varphi _0\circ \gamma _h$
. By Proposition 4.9 and Lemma 3.17, the arc
$\gamma :=\varphi _0\circ \gamma _h$
. By Proposition 4.9 and Lemma 3.17, the arc
![]() $\gamma $
is ambient isotopic rel
$\gamma $
is ambient isotopic rel
![]() $P(E_{\lambda _g})$
to a dynamic ray
$P(E_{\lambda _g})$
to a dynamic ray
![]() $g_{\underline {s}}$
landing at the singular value. Let
$g_{\underline {s}}$
landing at the singular value. Let
![]() $(\tilde {D}_i)_{i\in \mathbb {Z}}$
be the dynamical partition for
$(\tilde {D}_i)_{i\in \mathbb {Z}}$
be the dynamical partition for
![]() $E_{\lambda _g}$
with respect to
$E_{\lambda _g}$
with respect to
![]() $g_{\underline {s}}$
. As
$g_{\underline {s}}$
. As
![]() $\varphi _0$
restricts to a conjugation between
$\varphi _0$
restricts to a conjugation between
![]() $P(g)$
and
$P(g)$
and
![]() $P(E_{\lambda _g})$
, and as the ambient isotopy between
$P(E_{\lambda _g})$
, and as the ambient isotopy between
![]() $\gamma $
and
$\gamma $
and
![]() $g_{\underline {s}}$
does not move post-singular points, we have
$g_{\underline {s}}$
does not move post-singular points, we have
![]() $\varphi _0\circ \iota (\mathtt {p})\in \tilde {D}_{k_i}$
. Hence, the sector information of
$\varphi _0\circ \iota (\mathtt {p})\in \tilde {D}_{k_i}$
. Hence, the sector information of
![]() $\mathtt {H}$
and
$\mathtt {H}$
and
![]() $H_0$
is indeed consistent.
$H_0$
is indeed consistent.
This concludes the classification of psf exponential maps in terms of abstract exponential Hubbard trees.
7 Outlook
The key tools for our construction of homotopy Hubbard trees are dynamic rays, their landing properties, and the combinatorial encoding of both. It is natural to ask whether more general maps also have homotopy Hubbard trees. One putative obstacle is that the escaping set of an arbitrary post-singularly finite entire function need not consist of dynamic rays. Recently, the concept of dreadlocks has been introduced in [Reference Benini and RempeBR] as a generalization of dynamic rays. For every post-singularly finite entire function, the escaping set naturally decomposes into dreadlocks and the collection of dreadlocks can be encoded in terms of external addresses. Every repelling periodic point is the landing point of at least one and at most finitely many dreadlocks, all of which are periodic of the same period. In short, dreadlocks possess all the important properties needed to study the branching of the Julia set in terms of the escaping set. Using these findings, the existence and uniqueness of homotopy Hubbard trees for all post-singularly finite transcendental entire functions has been established based on a study of branch points of the Julia set in [Reference PfrangPf]. These results will be published in a series of forthcoming articles, the first of which is [Reference Pfrang, Petrat and SchleicherPPS].
Another interesting question that has not been answered in [Reference PfrangPf] is which post-singularly finite transcendental entire function has a Hubbard tree in the classical sense, that is, a compact embedded tree that is forward invariant as a set, not just forward invariant up to homotopy. By Theorem 3.4, psf exponential maps do not have a Hubbard tree essentially because of the existence of an asymptotic value. We expect this to be the only obstacle to the existence of Hubbard trees.
Acknowledgements
We gratefully acknowledge that this project was partially supported by a grant from the Deutsche Forschungsgemeinschaft, as well as by the Advanced Grant HOLOGRAM of the European Research Council. Major parts of this work were carried out at Jacobs University Bremen; other parts happened during a visit to Cornell University in the spring of 2018, for which we are grateful as well. We would like to thank Mikhail Hlushchanka, Russell Lodge, Dzmitry Dudko, Bernhard Reinke, John Hubbard, and Lasse Rempe for helpful discussions and comments. We would like to thank the anonymous referee for some helpful comments regarding the presentation.