A 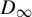$D_{\infty }$-topological Markov chain is a topological Markov chain provided with an action of the infinite dihedral group 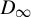$D_{\infty }$. It is defined by two zero-one square matrices A and J satisfying 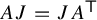$AJ=JA^{\textsf {T}}$ and 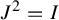$J^2=I$. A flip signature is obtained from symmetric bilinear forms with respect to J on the eventual kernel of A. We modify Williams’ decomposition theorem to prove the flip signature is a 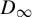$D_{\infty }$-conjugacy invariant. We introduce natural 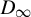$D_{\infty }$-actions on Ashley’s eight-by-eight and the full two-shift. The flip signatures show that Ashley’s eight-by-eight and the full two-shift equipped with the natural 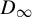$D_{\infty }$-actions are not 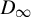$D_{\infty }$-conjugate. We also discuss the notion of 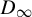$D_{\infty }$-shift equivalence and the Lind zeta function.