Article contents
Flexibility of measure-theoretic entropy of boundary maps associated to Fuchsian groups
Published online by Cambridge University Press: 14 April 2021
Abstract
Given a closed, orientable, compact surface S of constant negative curvature and genus 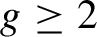 $g \geq 2$, we study the measure-theoretic entropy of the Bowen–Series boundary map with respect to its smooth invariant measure. We obtain an explicit formula for the entropy that only depends on the perimeter of the
$g \geq 2$, we study the measure-theoretic entropy of the Bowen–Series boundary map with respect to its smooth invariant measure. We obtain an explicit formula for the entropy that only depends on the perimeter of the 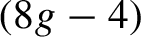 $(8g-4)$-sided fundamental polygon of the surface S and its genus. Using this, we analyze how the entropy changes in the Teichmüller space of S and prove the following flexibility result: the measure-theoretic entropy takes all values between 0 and a maximum that is achieved on the surface that admits a regular
$(8g-4)$-sided fundamental polygon of the surface S and its genus. Using this, we analyze how the entropy changes in the Teichmüller space of S and prove the following flexibility result: the measure-theoretic entropy takes all values between 0 and a maximum that is achieved on the surface that admits a regular 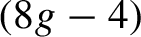 $(8g-4)$-sided fundamental polygon. We also compare the measure-theoretic entropy to the topological entropy of these maps and show that the smooth invariant measure is not a measure of maximal entropy.
$(8g-4)$-sided fundamental polygon. We also compare the measure-theoretic entropy to the topological entropy of these maps and show that the smooth invariant measure is not a measure of maximal entropy.
Information
- Type
- Original Article
- Information
- Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 389 - 401
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
In memory of Tolya
References
- 3
- Cited by


