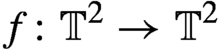Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiang, Miaohua
and
Lopez, Marco
2022.
SRB Entropy of Markov Transformations.
Journal of Statistical Physics,
Vol. 188,
Issue. 3,
Kucherenko, Tamara
and
Quas, Anthony
2025.
Realization of Anosov diffeomorphisms on the torus.
Journal of the London Mathematical Society,
Vol. 111,
Issue. 6,