1 Introduction
Let
![]() $(\mathcal M,g)$
be a smooth closed connected Riemannian manifold of dimension
$(\mathcal M,g)$
be a smooth closed connected Riemannian manifold of dimension
![]() $n\geq 3$
. We consider a smooth flow
$n\geq 3$
. We consider a smooth flow
![]() $\varphi _t$
on
$\varphi _t$
on
![]() $\mathcal M$
and its generating vector field
$\mathcal M$
and its generating vector field
Assumption 1. We suppose that the flow is Anosov, topologically transitive, and that the stable and unstable bundles are orientable and of dimension
![]() $d_s$
and
$d_s$
and
![]() $d_u$
, respectively. Furthermore, we consider a smooth, real valued potential V.
$d_u$
, respectively. Furthermore, we consider a smooth, real valued potential V.
1.1 Leading resonant state
We study the operator
![]() $\mathbf P:= -X+V$
acting on specially designed anisotropic Sobolev spaces. The sets of eigenvalues of
$\mathbf P:= -X+V$
acting on specially designed anisotropic Sobolev spaces. The sets of eigenvalues of
![]() $\mathbf P$
on these spaces are called the Ruelle resonances. Their set, which we will denote by
$\mathbf P$
on these spaces are called the Ruelle resonances. Their set, which we will denote by
![]() $\mathrm {Res}$
, is intrinsic to the Anosov flow and contains valuable dynamical meaning. Its understanding is essential to estimate the speed of decay of correlations, see for instance [Reference Liverani29, Reference Tsujii and Zhang37]. More concretely, Ruelle resonances are defined by (see for instance [Reference Dyatlov and Zworski16, Lemma 5.1])
$\mathrm {Res}$
, is intrinsic to the Anosov flow and contains valuable dynamical meaning. Its understanding is essential to estimate the speed of decay of correlations, see for instance [Reference Liverani29, Reference Tsujii and Zhang37]. More concretely, Ruelle resonances are defined by (see for instance [Reference Dyatlov and Zworski16, Lemma 5.1])
Here,
![]() $\mathrm {WF}(u)$
denotes the wavefront set of the distribution u and
$\mathrm {WF}(u)$
denotes the wavefront set of the distribution u and
![]() $E_u^{*}$
is the dual counterpart of the unstable bundle (see (20) for a precise definition).
$E_u^{*}$
is the dual counterpart of the unstable bundle (see (20) for a precise definition).
It is actually useful to study the operator
![]() $\mathbf P$
not only on functions but more generally on the space of k-forms in the kernel of the contraction by the flow:
$\mathbf P$
not only on functions but more generally on the space of k-forms in the kernel of the contraction by the flow:
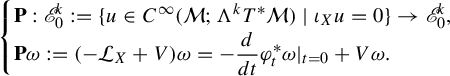 $$ \begin{align*} \begin{cases} \mathbf{P}: \mathscr E_0^k:=\{ u\in C^{\infty}(\mathcal M; \Lambda^k T^{*}\mathcal M) \mid \iota_{X}u=0\} \to \mathscr E_0^k,\\ \mathbf{P}\omega:=(-\mathcal L_X+V)\omega=-\displaystyle\frac{d}{dt}\varphi_t^{*}\omega|_{t=0}+ V\omega. \end{cases}\end{align*} $$
$$ \begin{align*} \begin{cases} \mathbf{P}: \mathscr E_0^k:=\{ u\in C^{\infty}(\mathcal M; \Lambda^k T^{*}\mathcal M) \mid \iota_{X}u=0\} \to \mathscr E_0^k,\\ \mathbf{P}\omega:=(-\mathcal L_X+V)\omega=-\displaystyle\frac{d}{dt}\varphi_t^{*}\omega|_{t=0}+ V\omega. \end{cases}\end{align*} $$
We can also define resonances for k-forms by the equivalence (1) and we denote their set by
![]() $\mathrm {Res}_k$
. (In this case, u should be a k-current, more precisely, in the dual of
$\mathrm {Res}_k$
. (In this case, u should be a k-current, more precisely, in the dual of
![]() $\mathscr E_0^k$
.) The decay rate of correlations is dictated by the resonances with large real part and hence of special interest is the study of resonances on the critical axis:
$\mathscr E_0^k$
.) The decay rate of correlations is dictated by the resonances with large real part and hence of special interest is the study of resonances on the critical axis:
Starting from the relation
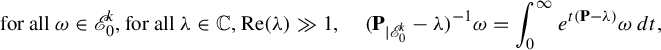 $$ \begin{align*} \text{for all } \omega \in {\mathscr E}_0^k, \text{for all } \unicode{x3bb} \in \mathbb C, \mathrm{Re}(\unicode{x3bb})\gg 1,\quad (\mathbf{P}_{|\mathscr E_0^k}-\unicode{x3bb})^{-1}\omega=\int_0^{\infty}e^{t(\mathbf{P}-\unicode{x3bb})}\omega\,dt, \end{align*} $$
$$ \begin{align*} \text{for all } \omega \in {\mathscr E}_0^k, \text{for all } \unicode{x3bb} \in \mathbb C, \mathrm{Re}(\unicode{x3bb})\gg 1,\quad (\mathbf{P}_{|\mathscr E_0^k}-\unicode{x3bb})^{-1}\omega=\int_0^{\infty}e^{t(\mathbf{P}-\unicode{x3bb})}\omega\,dt, \end{align*} $$
we see that the position of
![]() $\mathcal C_k$
should be linked to the exponential growth of the norm of the propagator
$\mathcal C_k$
should be linked to the exponential growth of the norm of the propagator
![]() $e^{t\mathbf {P}}$
on relevant functional spaces (the so-called anisotropic Sobolev spaces that will be introduced in §2.3). A form in
$e^{t\mathbf {P}}$
on relevant functional spaces (the so-called anisotropic Sobolev spaces that will be introduced in §2.3). A form in
![]() $\mathscr E_0^k$
is a linear combination of k-wegdes of elements of
$\mathscr E_0^k$
is a linear combination of k-wegdes of elements of
![]() $E_u^{*}$
and
$E_u^{*}$
and
![]() $E_s^{*}$
(see (12) for the exact definition of these bundles). However, an element in
$E_s^{*}$
(see (12) for the exact definition of these bundles). However, an element in
![]() $E_s^{*}$
is contracted exponentially fast while an element of
$E_s^{*}$
is contracted exponentially fast while an element of
![]() $E_u^{*}$
is expanded exponentially fast by the Anosov property. This means that to maximize the exponential growth of the norm, one should study the resolvent on
$E_u^{*}$
is expanded exponentially fast by the Anosov property. This means that to maximize the exponential growth of the norm, one should study the resolvent on
![]() $d_s$
-forms.
$d_s$
-forms.
Moreover, the exact location of
![]() $\mathcal C_0$
(respectively
$\mathcal C_0$
(respectively
![]() $\mathcal C_{d_s}$
) is given by the
$\mathcal C_{d_s}$
) is given by the
![]() ${P(V+J^u)}$
(respectively
${P(V+J^u)}$
(respectively
![]() $P(V)$
), where P denotes the topological pressure and
$P(V)$
), where P denotes the topological pressure and
![]() $J^u:=-({d}/{dt})\mathrm {det}(d\varphi _t(x)_{|E_u(x)})|_{t=0}$
is the unstable Jacobian. The corresponding eigenvectors (referred to as resonant states) also bear dynamical significance. More precisely, the resonant states at the first resonance
$J^u:=-({d}/{dt})\mathrm {det}(d\varphi _t(x)_{|E_u(x)})|_{t=0}$
is the unstable Jacobian. The corresponding eigenvectors (referred to as resonant states) also bear dynamical significance. More precisely, the resonant states at the first resonance
![]() $P(V+J^u)$
(respectively
$P(V+J^u)$
(respectively
![]() $P(V)$
) are linked to the system of leaf measures
$P(V)$
) are linked to the system of leaf measures
![]() $m^s_{V+J^u}$
(respectively
$m^s_{V+J^u}$
(respectively
![]() $m^s_V$
). Leaf measures are systems of reference measures on stable and unstable leaves which are used to obtain the equilibrium state via a product construction. Their introduction goes back to Sinai [Reference Sinai36] for maps and Margulis [Reference Margulis30] for flows (when
$m^s_V$
). Leaf measures are systems of reference measures on stable and unstable leaves which are used to obtain the equilibrium state via a product construction. Their introduction goes back to Sinai [Reference Sinai36] for maps and Margulis [Reference Margulis30] for flows (when
![]() $V=0$
). The measure of maximal entropy was obtained using leaf measures by Hamenstädt [Reference Hamenstädt22] for geodesic flows in negative curvature and by Hasselblatt [Reference Hasselblatt24] for Anosov flows, see also [Reference Hamenstädt23] for an extension to non-zero potentials. Recently, Climenhaga, Pesin, and Zelerowicz [Reference Climenhaga10–Reference Climenhaga, Pesin and Zelerowicz12] gave a new construction of leaf measures using dimension theory. Their construction extends to certain classes of partially hyperbolic flows, see also the related works of Carrasco and Rodriguez-Hertz [Reference Carrasco and Rodriguez-Hertz7, Reference Carrasco and Rodriguez-Hertz8].
$V=0$
). The measure of maximal entropy was obtained using leaf measures by Hamenstädt [Reference Hamenstädt22] for geodesic flows in negative curvature and by Hasselblatt [Reference Hasselblatt24] for Anosov flows, see also [Reference Hamenstädt23] for an extension to non-zero potentials. Recently, Climenhaga, Pesin, and Zelerowicz [Reference Climenhaga10–Reference Climenhaga, Pesin and Zelerowicz12] gave a new construction of leaf measures using dimension theory. Their construction extends to certain classes of partially hyperbolic flows, see also the related works of Carrasco and Rodriguez-Hertz [Reference Carrasco and Rodriguez-Hertz7, Reference Carrasco and Rodriguez-Hertz8].
Theorem 1.1. Under Assumption 1, the critical axes for the action on
![]() $0$
-forms and
$0$
-forms and
![]() $d_s$
-forms are given by
$d_s$
-forms are given by
Moreover,
![]() $ P(V+J^u)$
(respectively
$ P(V+J^u)$
(respectively
![]() $P(V))$
is a resonance called the first resonance for the action on
$P(V))$
is a resonance called the first resonance for the action on
![]() $0$
-forms (respectively
$0$
-forms (respectively
![]() $d_s$
-forms).
$d_s$
-forms).
There is
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $k\neq d_s$
, we have
$k\neq d_s$
, we have
![]() $\mathcal C_k\subset \{\unicode{x3bb} \mid \mathrm {Re}(\unicode{x3bb} )\leq P(V)-\delta \}$
, i.e., all other critical axes are to the left of
$\mathcal C_k\subset \{\unicode{x3bb} \mid \mathrm {Re}(\unicode{x3bb} )\leq P(V)-\delta \}$
, i.e., all other critical axes are to the left of
![]() $\mathcal C_{d_s}$
, see Figure 1. (For
$\mathcal C_{d_s}$
, see Figure 1. (For
![]() $1\leq k<l\leq d_s$
, the proof actually gives that
$1\leq k<l\leq d_s$
, the proof actually gives that
![]() $\mathcal C_l$
is to the right of
$\mathcal C_l$
is to the right of
![]() $\mathcal C_k$
.)
$\mathcal C_k$
.)
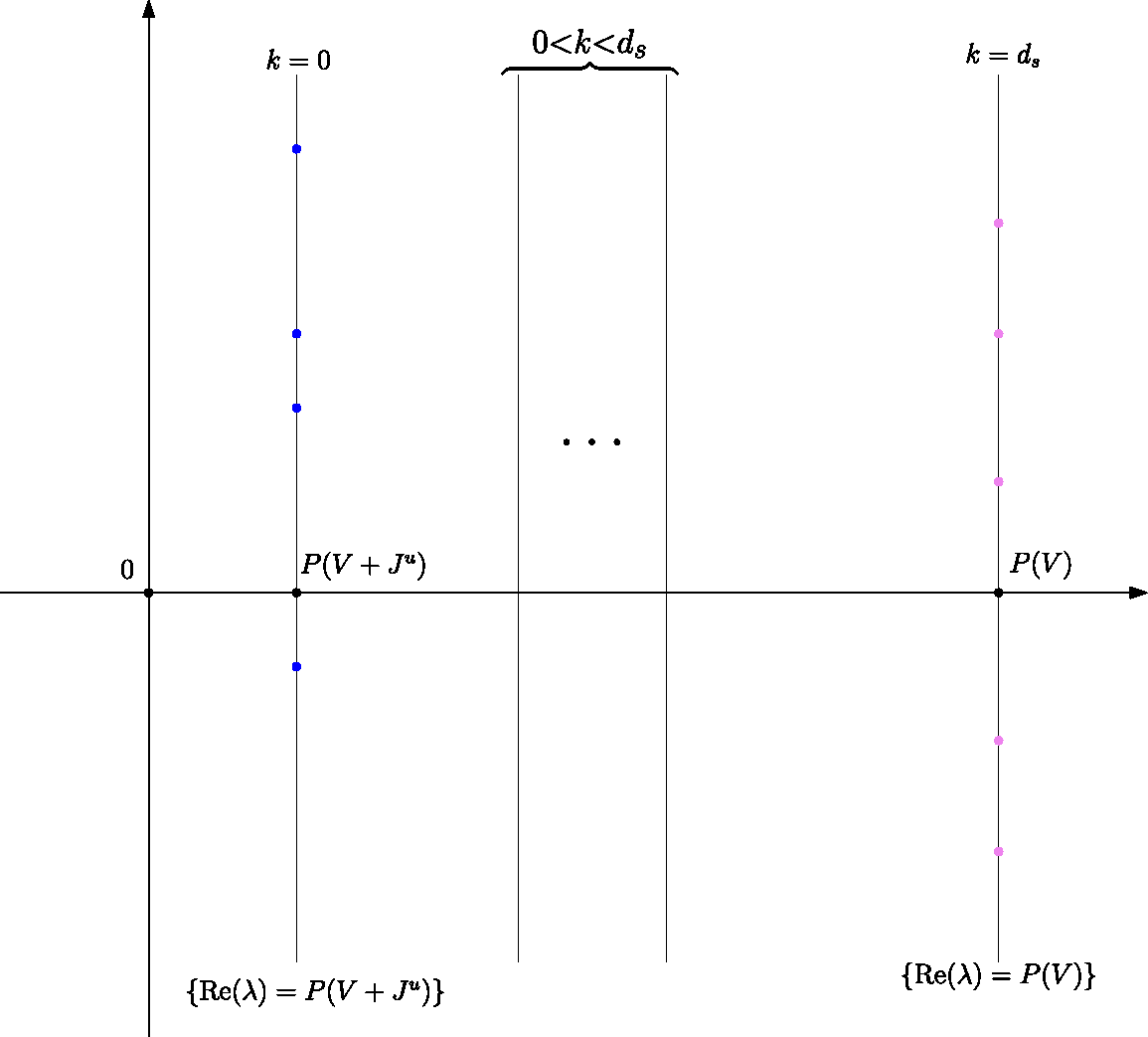
Figure 1 Critical axes for different values of k. According to Theorem 1.1, the resonances in purple cannot exist if the flow is weakly mixing with respect to
![]() $\mu _V$
and the resonances in blue cannot exist if the flow is weakly mixing with respect to
$\mu _V$
and the resonances in blue cannot exist if the flow is weakly mixing with respect to
![]() $\mu _{V+J^u}$
. The position of the critical axes for intermediate values of k should be linked to the pressure on the span of largest Lyapunov exponents.
$\mu _{V+J^u}$
. The position of the critical axes for intermediate values of k should be linked to the pressure on the span of largest Lyapunov exponents.
Moreover, all
![]() $\unicode{x3bb} \in \mathcal C_0$
(respectively
$\unicode{x3bb} \in \mathcal C_0$
(respectively
![]() $\unicode{x3bb} \in \mathcal C_{d_s})$
have no Jordan block and the first resonance
$\unicode{x3bb} \in \mathcal C_{d_s})$
have no Jordan block and the first resonance
![]() $P(V+J^u)$
(respectively
$P(V+J^u)$
(respectively
![]() $P(V))$
is simple:
$P(V))$
is simple:
where
![]() $\eta $
is a measure constructed in Theorem 3.1 from the system of leaf measures
$\eta $
is a measure constructed in Theorem 3.1 from the system of leaf measures
![]() $m^s_{V+J^u}$
.
$m^s_{V+J^u}$
.
We note that for hyperbolic maps, similar results were already obtained by various authors, using the formalism of anisotropic Banach spaces. The study for the action of
![]() $0$
-forms can be found in [Reference Baladi2, Theorem 7.5] and for
$0$
-forms can be found in [Reference Baladi2, Theorem 7.5] and for
![]() $d_s$
-forms, it can be found in [Reference Gouëzel and Liverani21, Theorem 5.1]. We also remark that Adam and Baladi used anisotropic techniques to study the first resonant state for a contact Anosov flows in dimension
$d_s$
-forms, it can be found in [Reference Gouëzel and Liverani21, Theorem 5.1]. We also remark that Adam and Baladi used anisotropic techniques to study the first resonant state for a contact Anosov flows in dimension
![]() $3$
for the potential
$3$
for the potential
![]() $V=-J^u$
in [Reference Adam and Baladi1]. (Because the unstable Jacobian is not smooth, this is actually, strictly speaking, out of the range of Theorem 1.1.)
$V=-J^u$
in [Reference Adam and Baladi1]. (Because the unstable Jacobian is not smooth, this is actually, strictly speaking, out of the range of Theorem 1.1.)
1.2 Equilibrium states
The leaf measures constructed in [Reference Climenhaga10–Reference Climenhaga, Pesin and Zelerowicz12] can be used to reconstruct the equilibrium state (i.e., the unique invariant probability measure that maximizes the variational principle recalled in (17)). In our context, this means that the equilibrium state can be reconstructed from the spectral theory of the Anosov vector field X. Define the divergence of X by the relation
![]() $\mathcal L_X \mathrm {vol}=\mathrm {div}_{\mathrm {vol}}(X) \mathrm {vol}$
for the Riemannian volume
$\mathcal L_X \mathrm {vol}=\mathrm {div}_{\mathrm {vol}}(X) \mathrm {vol}$
for the Riemannian volume
![]() $\mathrm {vol}$
. Then, the
$\mathrm {vol}$
. Then, the
![]() $L^2$
-adjoint of
$L^2$
-adjoint of
![]() $\mathbf P$
acting on
$\mathbf P$
acting on
![]() $0$
-forms is
$0$
-forms is
![]() $\mathbf P^{*}=X+V+\mathrm {div}_{\mathrm {vol}}(X).$
Applying Theorem 1.1 to the adjoint gives two co-resonant states
$\mathbf P^{*}=X+V+\mathrm {div}_{\mathrm {vol}}(X).$
Applying Theorem 1.1 to the adjoint gives two co-resonant states
![]() $\nu $
and
$\nu $
and
![]() $m^u_V$
, and one has
$m^u_V$
, and one has
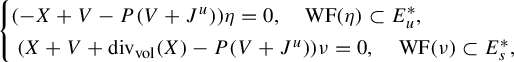 $$ \begin{align} \begin{cases}(-X+V-P(V+J^u))\eta=0,\quad \mathrm{WF}(\eta)\subset E_u^{*}, \\ \ (X+V+\mathrm{div}_{\mathrm{vol}}(X)-P(V+J^u))\nu=0,\quad \mathrm{WF}(\nu) \subset E_s^{*}, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases}(-X+V-P(V+J^u))\eta=0,\quad \mathrm{WF}(\eta)\subset E_u^{*}, \\ \ (X+V+\mathrm{div}_{\mathrm{vol}}(X)-P(V+J^u))\nu=0,\quad \mathrm{WF}(\nu) \subset E_s^{*}, \end{cases} \end{align} $$
as well as
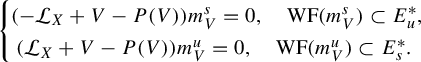 $$ \begin{align} \begin{cases} (-\mathcal L_X+V-P(V))m_V^s=0, \quad \mathrm{WF}(m^s_V)\subset E_u^{*}, \\ \ (\mathcal L_X+V-P(V))m_V^u=0,\quad \mathrm{WF}(m^u_V) \subset E_s^{*}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (-\mathcal L_X+V-P(V))m_V^s=0, \quad \mathrm{WF}(m^s_V)\subset E_u^{*}, \\ \ (\mathcal L_X+V-P(V))m_V^u=0,\quad \mathrm{WF}(m^u_V) \subset E_s^{*}. \end{cases} \end{align} $$
The wavefront set bounds allow us to take the distributional pairing of the resonant and co-resonant states
![]() $\eta $
and
$\eta $
and
![]() $\nu $
(respectively
$\nu $
(respectively
![]() $m^s_V$
and
$m^s_V$
and
![]() $m^u_V$
). The resulting distribution is easily seen to be measure invariant by the flow. The next theorem asserts that this measure is actually the equilibrium state for the potential
$m^u_V$
). The resulting distribution is easily seen to be measure invariant by the flow. The next theorem asserts that this measure is actually the equilibrium state for the potential
![]() $V+J^u$
(respectively V). As a consequence, the presence of other resonances on
$V+J^u$
(respectively V). As a consequence, the presence of other resonances on
![]() $\mathcal C_0$
(respectively
$\mathcal C_0$
(respectively
![]() $\mathcal C_{d_s})$
is linked to mixing properties of the flow. In the rest of the paper, we denote by
$\mathcal C_{d_s})$
is linked to mixing properties of the flow. In the rest of the paper, we denote by
![]() $\mu _W$
the equilibrium measure associated to the Hölder continuous potential W.
$\mu _W$
the equilibrium measure associated to the Hölder continuous potential W.
Theorem 1.2. Under Assumption 1, one has
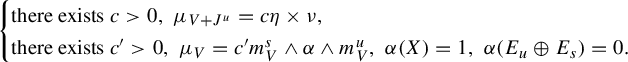 $$ \begin{align} \begin{cases} \text{there exists } c>0, \ \mu_{V+J^u}=c\eta \times \nu, \\ \text{there exists } c'>0, \ \mu_V=c'm^s_V\wedge \alpha \wedge m^u_V, \ \alpha(X)=1, \ \alpha(E_u\oplus E_s)=0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \text{there exists } c>0, \ \mu_{V+J^u}=c\eta \times \nu, \\ \text{there exists } c'>0, \ \mu_V=c'm^s_V\wedge \alpha \wedge m^u_V, \ \alpha(X)=1, \ \alpha(E_u\oplus E_s)=0. \end{cases} \end{align} $$
Let
![]() $\chi $
be a cutoff
$\chi $
be a cutoff
![]() $\chi \in C_c^{\infty }([0,T+\epsilon [, [0,1])$
such that
$\chi \in C_c^{\infty }([0,T+\epsilon [, [0,1])$
such that
![]() $\chi \equiv 1$
on
$\chi \equiv 1$
on
![]() $[0,T]$
for any
$[0,T]$
for any
![]() $\epsilon>0$
and for
$\epsilon>0$
and for
![]() $T>0$
large enough. Then, one has the following. (The notation
$T>0$
large enough. Then, one has the following. (The notation
![]() $f^{*k}$
denotes the kth convolution product of a function f with itself.)
$f^{*k}$
denotes the kth convolution product of a function f with itself.)
-
• For any
 $f\in C^{\infty }(\mathcal M)$
, (8)
$f\in C^{\infty }(\mathcal M)$
, (8) $$ \begin{align} -\lim_{k\to +\infty} \int_0^{+\infty}(\chi')^{*k}(t )((\varphi_t)_*\nu)(f)\,dt = c\mu_{V+J^u}(f), \quad c>0. \end{align} $$
$$ \begin{align} -\lim_{k\to +\infty} \int_0^{+\infty}(\chi')^{*k}(t )((\varphi_t)_*\nu)(f)\,dt = c\mu_{V+J^u}(f), \quad c>0. \end{align} $$
-
• Fix an orientation of
 $E_u^{*}$
and let
$E_u^{*}$
and let
 $\omega \in C^0(\mathcal M; \Lambda ^{d_s}E_u^{*})$
be a non-negative section which does not vanish identically. Then, one has, for any
$\omega \in C^0(\mathcal M; \Lambda ^{d_s}E_u^{*})$
be a non-negative section which does not vanish identically. Then, one has, for any
 $f\in C^{\infty }(\mathcal M)$
, (9)
$f\in C^{\infty }(\mathcal M)$
, (9) $$ \begin{align} -\lim_{k\to +\infty} \int_0^{+\infty}(\chi')^{*k}(t )((\varphi_t)_*(\omega \wedge \alpha \wedge m^u_V))(f)\,dt = c\mu_{V}(f), \quad c>0. \end{align} $$
$$ \begin{align} -\lim_{k\to +\infty} \int_0^{+\infty}(\chi')^{*k}(t )((\varphi_t)_*(\omega \wedge \alpha \wedge m^u_V))(f)\,dt = c\mu_{V}(f), \quad c>0. \end{align} $$
Finally, one has the following.
-
• If the flow is weakly mixing with respect to the equilibrium state
 $\mu _{V+J^u}$
, then
$\mu _{V+J^u}$
, then  $$ \begin{align*}\mathrm{Res}_0\cap \mathcal C_0=\{P(V+J^u)\}. \end{align*} $$
$$ \begin{align*}\mathrm{Res}_0\cap \mathcal C_0=\{P(V+J^u)\}. \end{align*} $$
-
• If the flow is weakly mixing with respect to the equilibrium state
 $\mu _{V}$
, then
$\mu _{V}$
, then  $$ \begin{align*}\mathrm{Res}_{d_s}\cap \mathcal C_{d_s}=\{P(V)\}. \end{align*} $$
$$ \begin{align*}\mathrm{Res}_{d_s}\cap \mathcal C_{d_s}=\{P(V)\}. \end{align*} $$
In particular, for
![]() $V=0$
, the theorem gives a construction of the Sinai–Ruelle–Bowen (SRB) measure for the action on
$V=0$
, the theorem gives a construction of the Sinai–Ruelle–Bowen (SRB) measure for the action on
![]() $0$
-forms (respectively the measure of maximal entropy for the action on
$0$
-forms (respectively the measure of maximal entropy for the action on
![]() $d_s$
-forms) from a solution of (5) (respectively (6)) for
$d_s$
-forms) from a solution of (5) (respectively (6)) for
![]() $P(J^u)=0$
(respectively for
$P(J^u)=0$
(respectively for
![]() $P(0)=\mathrm {h}_{\mathrm {top}}(\varphi _1)$
).
$P(0)=\mathrm {h}_{\mathrm {top}}(\varphi _1)$
).
1.3 Ruelle zeta function
The resolvents acting on
![]() $\mathscr E_0^k$
are linked to the (weighted) Ruelle zeta function:
$\mathscr E_0^k$
are linked to the (weighted) Ruelle zeta function:
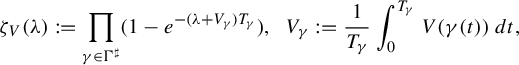 $$ \begin{align} \zeta_V(\unicode{x3bb}):=\prod_{{\gamma\in \Gamma^{\sharp}}}(1-e^{-(\unicode{x3bb}+V_{\gamma}) T_{\gamma}}), \ \ V_{\gamma}:=\frac{1}{T_{\gamma}}\int_0^{T_{\gamma}}V(\gamma(t))\,dt, \end{align} $$
$$ \begin{align} \zeta_V(\unicode{x3bb}):=\prod_{{\gamma\in \Gamma^{\sharp}}}(1-e^{-(\unicode{x3bb}+V_{\gamma}) T_{\gamma}}), \ \ V_{\gamma}:=\frac{1}{T_{\gamma}}\int_0^{T_{\gamma}}V(\gamma(t))\,dt, \end{align} $$
where
![]() $\Gamma ^{\sharp }$
is the set of primitive geodesics and
$\Gamma ^{\sharp }$
is the set of primitive geodesics and
![]() $T_{\gamma }$
denotes the period of the closed geodesic
$T_{\gamma }$
denotes the period of the closed geodesic
![]() $\gamma $
. This function can be shown to be convergent and holomorphic in a half-plane
$\gamma $
. This function can be shown to be convergent and holomorphic in a half-plane
![]() ${\{\mathrm {Re}(\unicode{x3bb} )\gg 1\}}$
. In a celebrated paper [Reference Giulietti, Liverani and Pollicott20], Giulietti, Liverani, and Pollicott proved that the function
${\{\mathrm {Re}(\unicode{x3bb} )\gg 1\}}$
. In a celebrated paper [Reference Giulietti, Liverani and Pollicott20], Giulietti, Liverani, and Pollicott proved that the function
![]() $\zeta _R^V$
admits a meromorphic extension to the whole complex plane. Another proof, using microlocal analysis, was given by Dyatlov and Zworski in [Reference Dyatlov, Faure and Guillarmou15].
$\zeta _R^V$
admits a meromorphic extension to the whole complex plane. Another proof, using microlocal analysis, was given by Dyatlov and Zworski in [Reference Dyatlov, Faure and Guillarmou15].
More precisely, let us introduce the Poincaré map
![]() $\mathcal P:\gamma \in \Gamma \mapsto \mathcal P_{\gamma }:=d\varphi _{-T_{\gamma }}|_{E_s\oplus E_u} $
. The link between the resolvents on forms and the Ruelle zeta function is given by the Guillemin trace formula. In particular, [Reference Dyatlov, Faure and Guillarmou15, equation (2.5)] gives
$\mathcal P:\gamma \in \Gamma \mapsto \mathcal P_{\gamma }:=d\varphi _{-T_{\gamma }}|_{E_s\oplus E_u} $
. The link between the resolvents on forms and the Ruelle zeta function is given by the Guillemin trace formula. In particular, [Reference Dyatlov, Faure and Guillarmou15, equation (2.5)] gives
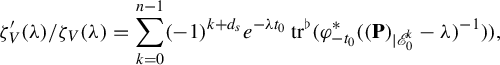 $$ \begin{align} \zeta_V^{\prime}(\unicode{x3bb})/\zeta_V(\unicode{x3bb})=\sum_{k=0}^{n-1}(-1)^{k+d_s} e^{-\unicode{x3bb} t_0}\operatorname{\mathrm{tr}}^{\flat}(\varphi_{-t_0}^{*} ((\mathbf{P})_{|\mathscr E_0^k}-\unicode{x3bb})^{-1}) ), \end{align} $$
$$ \begin{align} \zeta_V^{\prime}(\unicode{x3bb})/\zeta_V(\unicode{x3bb})=\sum_{k=0}^{n-1}(-1)^{k+d_s} e^{-\unicode{x3bb} t_0}\operatorname{\mathrm{tr}}^{\flat}(\varphi_{-t_0}^{*} ((\mathbf{P})_{|\mathscr E_0^k}-\unicode{x3bb})^{-1}) ), \end{align} $$
where the shift by a small time
![]() $t_0$
is a technicality to ensure that the pullbacked resolvent
$t_0$
is a technicality to ensure that the pullbacked resolvent
![]() $\varphi _{-t_0}^{*}(\mathbf {P}-\unicode{x3bb} )^{-1}$
satisfies the wavefront set condition which makes its flat trace well defined (see [Reference Dyatlov, Faure and Guillarmou15, §4]). This shows that the meromorphic extension of
$\varphi _{-t_0}^{*}(\mathbf {P}-\unicode{x3bb} )^{-1}$
satisfies the wavefront set condition which makes its flat trace well defined (see [Reference Dyatlov, Faure and Guillarmou15, §4]). This shows that the meromorphic extension of
![]() $\zeta _V$
follows from the extension of the resolvent acting on the space
$\zeta _V$
follows from the extension of the resolvent acting on the space
![]() $\mathscr E_0^k$
for any k (plus some additional arguments). Moreover, we get the poles of
$\mathscr E_0^k$
for any k (plus some additional arguments). Moreover, we get the poles of
![]() $\zeta _V$
by studying poles of each resolvent.
$\zeta _V$
by studying poles of each resolvent.
The study of the first pole of the Ruelle zeta function can be found in [Reference Parry and Pollicott31, Theorem 9.2].
Theorem. (Parry and Pollicott)
Let V be a Hölder continuous potential, and suppose that the flow is Anosov and weakly topologically mixing. Then, the Ruelle zeta function
![]() $\zeta _V$
is non-zero and analytic in the half-plane
$\zeta _V$
is non-zero and analytic in the half-plane
![]() $\{Re(\unicode{x3bb} )\geq P(V)\}$
except for a simple pole at
$\{Re(\unicode{x3bb} )\geq P(V)\}$
except for a simple pole at
![]() $\unicode{x3bb} =P(V)$
, where
$\unicode{x3bb} =P(V)$
, where
![]() $P(V)$
is the topological pressure of the potential V.
$P(V)$
is the topological pressure of the potential V.
As a consequence of our first two theorems, we recover the theorem of Parry and Pollicott on the first pole of the Ruelle zeta function for topologically mixing Anosov flows with smooth potentials.
We note that a consequence of this corollary and a standard Tauberian argument is the following asymptotic growth:
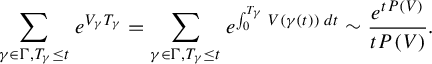 $$ \begin{align*}\sum_{\gamma \in \Gamma, T_{\gamma}\leq t}e^{V_{\gamma}T_{\gamma}}=\sum_{\gamma \in \Gamma, T_{\gamma}\leq t}e^{\int_0^{T_\gamma}V(\gamma(t))\,dt}\sim\frac{e^{tP(V)}}{tP(V)}. \end{align*} $$
$$ \begin{align*}\sum_{\gamma \in \Gamma, T_{\gamma}\leq t}e^{V_{\gamma}T_{\gamma}}=\sum_{\gamma \in \Gamma, T_{\gamma}\leq t}e^{\int_0^{T_\gamma}V(\gamma(t))\,dt}\sim\frac{e^{tP(V)}}{tP(V)}. \end{align*} $$
For
![]() $V=0$
, this result is known as the prime orbit theorem and can be found in [Reference Parry and Pollicott31, Theorem 9.3].
$V=0$
, this result is known as the prime orbit theorem and can be found in [Reference Parry and Pollicott31, Theorem 9.3].
1.4 Regularity of the pressure
Another consequence of our first theorems is the following regularity statement of the topological pressure. It was first established by Katok et al in [Reference Katok, Pollicott and Knieper27] and Contreras in [Reference Contreras13].
Corollary 1.1. (Smoothness of the topological pressure)
Let
![]() $\mathcal V^{\infty }_{\mathrm {t}}$
denote the set of smooth transitive Anosov flows. Then, it is an open set (this point follows from [
Reference Fisher and Hasselblatt19
, Proposition 1.6.30] which proves that topological transitivity is preserved by orbit conjugacy and the structural stability of Anosov flows, see [Reference Fisher and Hasselblatt19, Corollary 5.4.7]) and the maps
$\mathcal V^{\infty }_{\mathrm {t}}$
denote the set of smooth transitive Anosov flows. Then, it is an open set (this point follows from [
Reference Fisher and Hasselblatt19
, Proposition 1.6.30] which proves that topological transitivity is preserved by orbit conjugacy and the structural stability of Anosov flows, see [Reference Fisher and Hasselblatt19, Corollary 5.4.7]) and the maps
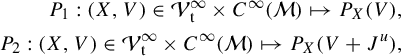 $$ \begin{align*}P_1: (X,V)\in \mathcal V^{\infty}_{\mathrm{t}}\times C^{\infty}(\mathcal M)\mapsto P_X(V),\\ P_2: (X,V)\in \mathcal V^{\infty}_{\mathrm{t}}\times C^{\infty}(\mathcal M)\mapsto P_X(V+J^u), \end{align*} $$
$$ \begin{align*}P_1: (X,V)\in \mathcal V^{\infty}_{\mathrm{t}}\times C^{\infty}(\mathcal M)\mapsto P_X(V),\\ P_2: (X,V)\in \mathcal V^{\infty}_{\mathrm{t}}\times C^{\infty}(\mathcal M)\mapsto P_X(V+J^u), \end{align*} $$
where
![]() $P_X$
denotes the topological pressure for the flow induced by the vector field X, are smooth.
$P_X$
denotes the topological pressure for the flow induced by the vector field X, are smooth.
1.5 Outline of article
-
• In §2, we recall some important features of Anosov flows and of the thermodynamical formalism. Then, we will review microlocal methods for the study of Anosov flows. Finally, we will recall the construction of leaf measures.
-
• In §3, we recall the definition of Ruelle resonances using a parametrix construction. Then, we define in Theorem 3.1 a co-resonant state for the action on
 $0$
-forms. This allows us to precisely locate the critical axis at
$0$
-forms. This allows us to precisely locate the critical axis at
 $\{\mathrm {Re}(\unicode{x3bb} )=P(V+J^u)\}$
. The rest of the section is devoted to the study of resonant states on the critical axis and more precisely to the proofs of the results announced in §1.
$\{\mathrm {Re}(\unicode{x3bb} )=P(V+J^u)\}$
. The rest of the section is devoted to the study of resonant states on the critical axis and more precisely to the proofs of the results announced in §1. -
• In §4, we prove the equivalent results for the action on
 $d_s$
-forms. The strategies of the proofs remain the same, but some additional care is needed when adapting certain arguments to this case.
$d_s$
-forms. The strategies of the proofs remain the same, but some additional care is needed when adapting certain arguments to this case. -
• In §5, we give a proof of the first part of Theorem 1.1 and of Corollary 1.1.
2 Preliminaries
2.1 Anosov flow
Our main assumption on the flow is that it is Anosov.
Definition 2.1. (Anosov)
The flow
![]() $\varphi _t$
is Anosov (or uniformly hyperbolic) if:
$\varphi _t$
is Anosov (or uniformly hyperbolic) if:
-
• there is a continuous splitting of the tangent space
(12) $$ \begin{align} T_x\mathcal M=E_u(x)\oplus E_s(x)\oplus \mathbb R X(x); \end{align} $$
$$ \begin{align} T_x\mathcal M=E_u(x)\oplus E_s(x)\oplus \mathbb R X(x); \end{align} $$
-
• the decomposition is flow-invariant, meaning that
(13) $$ \begin{align} \text{ for all } t\in \mathbb R,\quad E_u(\varphi_t(x))=(d\varphi_t)_x( E_u(x)),\quad E_s(\varphi_t(x))=(d\varphi_t)_x( E_s(x)); \end{align} $$
$$ \begin{align} \text{ for all } t\in \mathbb R,\quad E_u(\varphi_t(x))=(d\varphi_t)_x( E_u(x)),\quad E_s(\varphi_t(x))=(d\varphi_t)_x( E_s(x)); \end{align} $$
-
• there are uniform constants
 $C>0$
and
$C>0$
and
 $\theta>0$
such that for every
$\theta>0$
such that for every
 $x\in M$
, we have
$x\in M$
, we have  $$ \begin{align*}|(d\varphi_t)_x(v_s)|_g\leq Ce^{-\theta t}|v_s|_g \quad \text{for all } t\geq 0, \text{ for all } v_s\in E_s(x).\end{align*} $$
$$ \begin{align*}|(d\varphi_t)_x(v_s)|_g\leq Ce^{-\theta t}|v_s|_g \quad \text{for all } t\geq 0, \text{ for all } v_s\in E_s(x).\end{align*} $$
 $$ \begin{align*}|(d\varphi_t)_x(v_u)|_g\leq Ce^{-\theta |t|}|v_u|_g\quad\text{for all } t\leq 0, \text{ for all } v_u\in E_u(x).\end{align*} $$
$$ \begin{align*}|(d\varphi_t)_x(v_u)|_g\leq Ce^{-\theta |t|}|v_u|_g\quad\text{for all } t\leq 0, \text{ for all } v_u\in E_u(x).\end{align*} $$
We will denote by
![]() $d_u$
and
$d_u$
and
![]() $d_s$
the dimensions of
$d_s$
the dimensions of
![]() $E_u$
and
$E_u$
and
![]() $E_s$
, respectively.
$E_s$
, respectively.
For a comprehensive introduction to the theory of Anosov flows, we refer to [Reference Fisher and Hasselblatt19, Ch. 8]. An important class of examples is given by geodesic flows on the unit tangent bundle
![]() $\mathcal M=SM$
of a negatively curved closed Riemannian manifold M. We recall the stable manifold theorem, see for instance [Reference Hasselblatt and Katok25, Theorem 6.4.9].
$\mathcal M=SM$
of a negatively curved closed Riemannian manifold M. We recall the stable manifold theorem, see for instance [Reference Hasselblatt and Katok25, Theorem 6.4.9].
For all
![]() $x\in \mathcal M$
, there exists immersed submanifolds
$x\in \mathcal M$
, there exists immersed submanifolds
where
![]() $+$
(respectively
$+$
(respectively
![]() $-$
) corresponds to s (respectively u), called the (strong) stable (respectively unstable) manifolds, such that
$-$
) corresponds to s (respectively u), called the (strong) stable (respectively unstable) manifolds, such that
![]() $ T_x \mathcal W^{s,u}=E_{s,u}.$
Moreover,
$ T_x \mathcal W^{s,u}=E_{s,u}.$
Moreover,
![]() $x\mapsto \mathcal W^{s,u}(x)$
are (Hölder continuous) foliations of
$x\mapsto \mathcal W^{s,u}(x)$
are (Hölder continuous) foliations of
![]() $\mathcal M$
. We also define the weak stable and unstable manifolds
$\mathcal M$
. We also define the weak stable and unstable manifolds
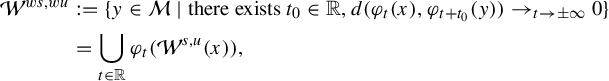 $$ \begin{align} \mathcal W^{ws,wu}&:=\{y\in \mathcal M\mid \text{there exists } t_0\in \mathbb R, d(\varphi_{t}(x), \varphi_{t+t_0}(y))\to_{t\to \pm\infty}0\}\notag\\ &=\bigcup_{t\in \mathbb R}\varphi_t(\mathcal W^{s,u}(x)), \end{align} $$
$$ \begin{align} \mathcal W^{ws,wu}&:=\{y\in \mathcal M\mid \text{there exists } t_0\in \mathbb R, d(\varphi_{t}(x), \varphi_{t+t_0}(y))\to_{t\to \pm\infty}0\}\notag\\ &=\bigcup_{t\in \mathbb R}\varphi_t(\mathcal W^{s,u}(x)), \end{align} $$
their tangent spaces are given respectively by
![]() $\mathbb R X\oplus E_s$
and
$\mathbb R X\oplus E_s$
and
![]() $\mathbb R X\oplus E_u$
.
$\mathbb R X\oplus E_u$
.
A consequence of the existence of these (un)stable manifolds is the local product structure, see [Reference Hasselblatt and Katok25, Proposition 6.4.13].
For any
![]() $x_0\in \mathcal M$
, there exists a neighborhood V of
$x_0\in \mathcal M$
, there exists a neighborhood V of
![]() $x_0$
such that for any
$x_0$
such that for any
![]() $\epsilon>0$
, there is a
$\epsilon>0$
, there is a
![]() $\delta>0$
such that
$\delta>0$
such that
where we denoted by
![]() $\mathcal N_{\epsilon }$
the
$\mathcal N_{\epsilon }$
the
![]() $\epsilon $
-ball of the manifold
$\epsilon $
-ball of the manifold
![]() $\mathcal N$
. The point
$\mathcal N$
. The point
![]() $[x,y]$
is called the Bowen bracket of x and y, and
$[x,y]$
is called the Bowen bracket of x and y, and
![]() $t(x,y)$
is the Bowen time. For
$t(x,y)$
is the Bowen time. For
![]() $q\in \mathcal M$
, we define a local rectangle to be
$q\in \mathcal M$
, we define a local rectangle to be
2.2 Thermodynamical formalism
We recall here the main features from the thermodynamical formalism we will need. The two main objects are the topological pressure and the equilibrium state. For an introduction to the thermodynamical formalism, we refer to [Reference Fisher and Hasselblatt19, Ch. 4]. Consider a Hölder continuous and real valued potential V.
We first recall the variational principle (see [Reference Fisher and Hasselblatt19, Theorem 9.3.4]), which we will state in the case of smooth flows.
Let
![]() $(\mathcal M,g)$
be a closed Riemannian manifold and
$(\mathcal M,g)$
be a closed Riemannian manifold and
![]() $\varphi _t$
be a smooth flow on
$\varphi _t$
be a smooth flow on
![]() $\mathcal M$
, and let
$\mathcal M$
, and let
![]() $V:\mathcal M \to \mathbb R$
be a Hölder continuous potential, then
$V:\mathcal M \to \mathbb R$
be a Hölder continuous potential, then
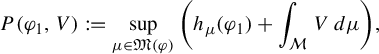 $$ \begin{align} P(\varphi_1,V):=\sup_{\mu \in \mathfrak M(\varphi)} \bigg(h_{\mu}(\varphi_1)+\int_{\mathcal M}V\,d\mu\bigg), \end{align} $$
$$ \begin{align} P(\varphi_1,V):=\sup_{\mu \in \mathfrak M(\varphi)} \bigg(h_{\mu}(\varphi_1)+\int_{\mathcal M}V\,d\mu\bigg), \end{align} $$
where
![]() $h_{\mu }$
is the metric entropy and
$h_{\mu }$
is the metric entropy and
![]() $\mathfrak M(\varphi )$
is the set of invariant-probability Borel measures, and
$\mathfrak M(\varphi )$
is the set of invariant-probability Borel measures, and
![]() $P(\varphi _1,V)$
is the topological pressure associated to V.
$P(\varphi _1,V)$
is the topological pressure associated to V.
Now, we can define an equilibrium state as a measure that achieves the supremum, where the existence and uniqueness of such a measure can be obtained under Assumption 1, and we will use the following result (see [Reference Fisher and Hasselblatt19, Theorem 7.3.6] and [Reference Bowen and Ruelle6, Theorem 3.3]).
Proposition 2.1. (Existence and uniqueness of equilibrium states)
Under Assumption 1, the equilibrium state associated to V is unique, ergodic, and has full support. If the flow is topologically mixing, then the flow is weak mixing with respect to the equilibrium state
![]() $\mu _V$
.
$\mu _V$
.
In the case of an Anosov flow, an equivalent characterization of equilibrium state is given by the Gibbs property (see [Reference Fisher and Hasselblatt19, Theorem 4.3.26]). Indeed,
![]() $\mu $
is the equilibrium state for V if and only if
$\mu $
is the equilibrium state for V if and only if
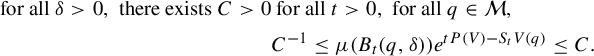 $$ \begin{align} \text{for all } \delta>0, \text{ there exists } C>0 &\text{ for all } t>0, \text{ for all } q\in \mathcal M, \notag\\ &C^{-1}\leq \mu(B_t(q,\delta))e^{tP(V)-S_tV(q)}\leq C. \end{align} $$
$$ \begin{align} \text{for all } \delta>0, \text{ there exists } C>0 &\text{ for all } t>0, \text{ for all } q\in \mathcal M, \notag\\ &C^{-1}\leq \mu(B_t(q,\delta))e^{tP(V)-S_tV(q)}\leq C. \end{align} $$
Here,
![]() $B_t(q,\delta )$
denotes the Bowen ball defined in (28) and
$B_t(q,\delta )$
denotes the Bowen ball defined in (28) and
![]() $S_tV(q):=\int _0^tV(\varphi _s q)\,ds.$
$S_tV(q):=\int _0^tV(\varphi _s q)\,ds.$
We define a special potential called the unstable Jacobian by the following formula:
where the determinant is taken with respect to the Riemannian measure
![]() $\mathrm {vol}$
.
$\mathrm {vol}$
.
The equilibrium state associated to the unstable Jacobian is the SRB measure whose pressure vanishes:
![]() $P(J^u)=0$
, see [Reference Fisher and Hasselblatt19, Corollary 7.4.5].
$P(J^u)=0$
, see [Reference Fisher and Hasselblatt19, Corollary 7.4.5].
2.3 Anisotropic spaces
To a given decomposition (12), we can associate a corresponding splitting of the cotangent space. This will be more natural as we will use microlocal analysis. For an introduction to microlocal analysis, we refer the reader to [Reference Zworski39].
There is a continuous splitting
![]() $ T^{*}_xM=E_u^{*}(x)\oplus E_s^{*}(x)\oplus E_0^{*}(x), $
defined by
$ T^{*}_xM=E_u^{*}(x)\oplus E_s^{*}(x)\oplus E_0^{*}(x), $
defined by
Moreover, this decomposition is flow-invariant and there exists constants
![]() $C,\theta>0$
such that, uniformly in
$C,\theta>0$
such that, uniformly in
![]() $x\in M$
, we have
$x\in M$
, we have
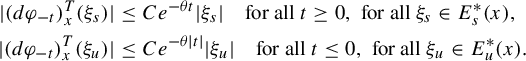 $$ \begin{align*} |(d\varphi_{-t})^T_x(\xi_s)|&\leq Ce^{-\theta t}|\xi_s|\quad \text{for all } t\geq 0, \ \text{for all } \xi_s\in E_s^{*}(x),\\ |(d\varphi_{-t})^T_x(\xi_u)|&\leq Ce^{-\theta |t|}|\xi_u|\quad \text{for all } t\leq 0, \ \text{for all } \xi_u\in E_u^{*}(x). \end{align*} $$
$$ \begin{align*} |(d\varphi_{-t})^T_x(\xi_s)|&\leq Ce^{-\theta t}|\xi_s|\quad \text{for all } t\geq 0, \ \text{for all } \xi_s\in E_s^{*}(x),\\ |(d\varphi_{-t})^T_x(\xi_u)|&\leq Ce^{-\theta |t|}|\xi_u|\quad \text{for all } t\leq 0, \ \text{for all } \xi_u\in E_u^{*}(x). \end{align*} $$
The following result, which is due to Faure, Roy, and Sjöstrand in [Reference Faure, Roy and Sjöstrand17] constructs an anisotropic order function.
There exists an order function
![]() $m(x,\xi )$
taking its values in
$m(x,\xi )$
taking its values in
![]() $[-1,1]$
and an escape function
$[-1,1]$
and an escape function
![]() $G_m(x,\xi ):=m(x,\xi )\log |\xi |, $
such that:
$G_m(x,\xi ):=m(x,\xi )\log |\xi |, $
such that:
-
• the order function
 $m(x,\xi )$
only depends on the direction
$m(x,\xi )$
only depends on the direction
 $\xi /|\xi |\in S^{*}M$
for
$\xi /|\xi |\in S^{*}M$
for
 $|\xi |\geq 1$
and is equal to
$|\xi |\geq 1$
and is equal to
 $1$
(respectively
$1$
(respectively
 $-1)$
in a conical neighborhood of
$-1)$
in a conical neighborhood of
 $E_s^{*}$
(respectively
$E_s^{*}$
(respectively
 $E_u^{*})$
;
$E_u^{*})$
; -
• the escape function decreases along trajectories, that is,
(For this inequality, one should work with an adapted metric and $$ \begin{align*}\text{there exists } R>0,|\xi|\geq R,\quad \mathbf{X}(G_m)(x,\xi)\leq 0. \end{align*} $$
$$ \begin{align*}\text{there exists } R>0,|\xi|\geq R,\quad \mathbf{X}(G_m)(x,\xi)\leq 0. \end{align*} $$
 $\mathbf {X}$
denotes the symplectic lift of the vector field X.)
$\mathbf {X}$
denotes the symplectic lift of the vector field X.)
We fix now an order function m and consider the corresponding symbol class. We refer to [Reference Faure, Roy and Sjöstrand17, Appendix] for the detailed construction. What is important to understand here is that the order function
![]() $m(x,\xi )$
constructed below gives rise to a symbol class
$m(x,\xi )$
constructed below gives rise to a symbol class
![]() $S^{m(x,\xi )}$
on which we can perform quantization. These quantized symbols are called pseudo-differential operators of order
$S^{m(x,\xi )}$
on which we can perform quantization. These quantized symbols are called pseudo-differential operators of order
![]() $m(x,\xi )$
and can be viewed as bounded operators from the anisotropic Sobolev space
$m(x,\xi )$
and can be viewed as bounded operators from the anisotropic Sobolev space
![]() $H^{m(x,\xi )}$
to
$H^{m(x,\xi )}$
to
![]() $L^2(M)$
. The anisotropic Sobolev space
$L^2(M)$
. The anisotropic Sobolev space
![]() $H^{m(x,\xi )}$
is defined by means of an elliptic operator in the anisotropic symbol class
$H^{m(x,\xi )}$
is defined by means of an elliptic operator in the anisotropic symbol class
![]() $S^{m(x,\xi )}_{\rho }$
(see [Reference Faure, Roy and Sjöstrand17, Appendix, Definition 7]).
$S^{m(x,\xi )}_{\rho }$
(see [Reference Faure, Roy and Sjöstrand17, Appendix, Definition 7]).
The symbol
![]() $\exp (G_m)$
belongs to the anisotropic class
$\exp (G_m)$
belongs to the anisotropic class
![]() $S^{m(x,\xi )}_{\rho }$
for every
$S^{m(x,\xi )}_{\rho }$
for every
![]() $\rho <1$
, and if we fix a quantization
$\rho <1$
, and if we fix a quantization
![]() $\mathrm {Op}$
(see for instance [Reference Zworski39, Ch. 4]),
$\mathrm {Op}$
(see for instance [Reference Zworski39, Ch. 4]),
is a pseudo-differential operator which is elliptic and, up to changing the symbol by a
![]() $O(S^{m(x,\xi )-(2\rho -1)})$
term, it can be made formally self-adjoint and invertible on
$O(S^{m(x,\xi )-(2\rho -1)})$
term, it can be made formally self-adjoint and invertible on
![]() $C^{\infty }(M)$
. For
$C^{\infty }(M)$
. For
![]() $s\in \mathbb R$
, we define the Sobolev space of order
$s\in \mathbb R$
, we define the Sobolev space of order
![]() $sm(x,\xi )$
to be
$sm(x,\xi )$
to be
![]() $ \mathcal H^s:=\hat A_{sm}^{-1}(L^2(M)).$
In the following, the
$ \mathcal H^s:=\hat A_{sm}^{-1}(L^2(M)).$
In the following, the
![]() $L^2$
spaces will be associated to the Riemannian volume form
$L^2$
spaces will be associated to the Riemannian volume form
![]() $\mathrm {vol}$
. The following properties hold:
$\mathrm {vol}$
. The following properties hold:
-
• the space
 $\mathcal H^s$
is a Hilbert space with inner product which makes
$\mathcal H^s$
is a Hilbert space with inner product which makes $$ \begin{align*}(\varphi_1,\varphi_2)_{\mathcal H^s}:=(\hat A_{sm} \varphi_1,\hat A_{sm} \varphi_2)_{L^2}, \end{align*} $$
$$ \begin{align*}(\varphi_1,\varphi_2)_{\mathcal H^s}:=(\hat A_{sm} \varphi_1,\hat A_{sm} \varphi_2)_{L^2}, \end{align*} $$
 $\hat A_{sm}$
a unitary operator from
$\hat A_{sm}$
a unitary operator from
 $\mathcal H^s$
to
$\mathcal H^s$
to
 $L^2$
;
$L^2$
;
-
• for a pseudo-differential operator
 $A\in \Psi ^{sm(x,\xi )}$
, A is an unbounded operator on
$A\in \Psi ^{sm(x,\xi )}$
, A is an unbounded operator on
 $L^2(M)$
with domain given by
$L^2(M)$
with domain given by
 $\mathcal H^s$
;
$\mathcal H^s$
; -
• the space
 $\mathcal H^{-s}$
can be identified to the dual of
$\mathcal H^{-s}$
can be identified to the dual of
 $\mathcal H^s$
by (21)and the duality extends the usual
$\mathcal H^s$
by (21)and the duality extends the usual $$ \begin{align} (\varphi,\psi)_{\mathcal H^s\times \mathcal H^{-s}}:=(\hat A_{sm} \varphi, \hat A_{sm}^{-1} \psi)_{L^2}, \end{align} $$
$$ \begin{align} (\varphi,\psi)_{\mathcal H^s\times \mathcal H^{-s}}:=(\hat A_{sm} \varphi, \hat A_{sm}^{-1} \psi)_{L^2}, \end{align} $$
 $L^2$
-pairing;
$L^2$
-pairing;
-
• if
 $f\in C^{\infty }(\mathcal M)$
, then for any
$f\in C^{\infty }(\mathcal M)$
, then for any
 $ \varphi \in \mathcal H^s, \ \psi \in \mathcal H^{-s}$
, (22)
$ \varphi \in \mathcal H^s, \ \psi \in \mathcal H^{-s}$
, (22) $$ \begin{align} (f\varphi,\psi)_{\mathcal H^s\times \mathcal H^{-s}}=(\varphi,\bar f\psi)_{\mathcal H^s\times \mathcal H^{-s}}. \end{align} $$
$$ \begin{align} (f\varphi,\psi)_{\mathcal H^s\times \mathcal H^{-s}}=(\varphi,\bar f\psi)_{\mathcal H^s\times \mathcal H^{-s}}. \end{align} $$
We now use the microlocal techniques introduced in [Reference Faure, Roy and Sjöstrand17, Reference Faure and Sjöstrand18] to define the Ruelle resonances. We first define the transfer operator associated to the Anosov flow.
The transfer operator
![]() $e^{t \mathbf P}: L^2(\mathcal M, \mathrm {vol}) \to L^2(\mathcal M,\mathrm {vol})$
(where
$e^{t \mathbf P}: L^2(\mathcal M, \mathrm {vol}) \to L^2(\mathcal M,\mathrm {vol})$
(where
![]() $\mathbf {P}:=-X+V$
) is given, for any
$\mathbf {P}:=-X+V$
) is given, for any
![]() $f\in C^{\infty }(M)$
, by
$f\in C^{\infty }(M)$
, by
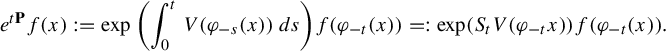 $$ \begin{align*}e^{t \mathbf P}f(x):=\exp\bigg(\!\int_0^t V(\varphi_{-s}(x))\,ds\bigg)f(\varphi_{-t}(x))=:\exp (S_tV(\varphi_{-t}x))f(\varphi_{-t}(x)). \end{align*} $$
$$ \begin{align*}e^{t \mathbf P}f(x):=\exp\bigg(\!\int_0^t V(\varphi_{-s}(x))\,ds\bigg)f(\varphi_{-t}(x))=:\exp (S_tV(\varphi_{-t}x))f(\varphi_{-t}(x)). \end{align*} $$
We define the exponential growth in the
![]() $L^2$
-norm of
$L^2$
-norm of
![]() $e^{t\mathbf {P}}$
by
$e^{t\mathbf {P}}$
by
The fact that
![]() $C_0$
is finite is a consequence of
$C_0$
is finite is a consequence of
![]() $e^{t\mathbf {P}}$
being a semi-group.
$e^{t\mathbf {P}}$
being a semi-group.
We obtain the existence of the meromorphic extension of the resolvent to the whole complex plane and the fact that Ruelle resonances are contained in
![]() $\{\mathrm {Re}(\unicode{x3bb} )\leq C_0\}$
. We refer to [Reference Lefeuvre28, Theorem 9.11] for a proof of the following theorem.
$\{\mathrm {Re}(\unicode{x3bb} )\leq C_0\}$
. We refer to [Reference Lefeuvre28, Theorem 9.11] for a proof of the following theorem.
Theorem 2.1. (Faure and Sjöstrand)
There exists
![]() $c>0$
such that for any
$c>0$
such that for any
![]() $s> 0$
, we have, for any
$s> 0$
, we have, for any
![]() $\unicode{x3bb} $
such that
$\unicode{x3bb} $
such that
![]() $\mathrm {Re}(\unicode{x3bb} )> -cs+C_0$
, that
$\mathrm {Re}(\unicode{x3bb} )> -cs+C_0$
, that
![]() $\mathbf {P}-\unicode{x3bb} $
is Fredholm of index
$\mathbf {P}-\unicode{x3bb} $
is Fredholm of index
![]() $0$
as an operator
$0$
as an operator
Moreover, the resolvent
is well defined, bounded, and holomorphic for
![]() $\{\mathrm {Re}(\unicode{x3bb} )> C_0\}$
and has a meromorphic extension to
$\{\mathrm {Re}(\unicode{x3bb} )> C_0\}$
and has a meromorphic extension to
![]() $\{\mathrm {Re}(\unicode{x3bb} )> -cs+C_0\}$
, which is independent of any choice. Thus, the resolvent, viewed as an operator
$\{\mathrm {Re}(\unicode{x3bb} )> -cs+C_0\}$
, which is independent of any choice. Thus, the resolvent, viewed as an operator
![]() $C^{\infty }(M)\to \mathcal D'(M)$
, has a meromorphic extension to the whole complex plane. The poles of this extension are called the Ruelle resonances, and they are located in
$C^{\infty }(M)\to \mathcal D'(M)$
, has a meromorphic extension to the whole complex plane. The poles of this extension are called the Ruelle resonances, and they are located in
![]() $\{\mathrm {Re}(\unicode{x3bb} )\leq C_0\}$
. On
$\{\mathrm {Re}(\unicode{x3bb} )\leq C_0\}$
. On
![]() $\{\mathrm {Re}(\unicode{x3bb} )> C_0\}$
, one has
$\{\mathrm {Re}(\unicode{x3bb} )> C_0\}$
, one has
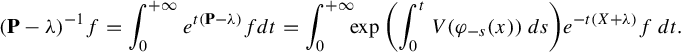 $$ \begin{align} (\mathbf{P}-\unicode{x3bb})^{-1}f=\int_{0}^{+\infty}e^{t(\mathbf{P}-\unicode{x3bb})}fdt=\int_{0}^{+\infty}\!\!\exp\bigg(\!\int_0^t V(\varphi_{-s}(x))\,ds\bigg)e^{-t({X}+\unicode{x3bb})}f\,dt. \end{align} $$
$$ \begin{align} (\mathbf{P}-\unicode{x3bb})^{-1}f=\int_{0}^{+\infty}e^{t(\mathbf{P}-\unicode{x3bb})}fdt=\int_{0}^{+\infty}\!\!\exp\bigg(\!\int_0^t V(\varphi_{-s}(x))\,ds\bigg)e^{-t({X}+\unicode{x3bb})}f\,dt. \end{align} $$
Remark 2.1. The previous construction can be made for a general smooth Hermitian bundle
![]() $\mathscr E$
and in particular for the bundle of forms in the kernel of the contraction, see [Reference Dyatlov, Faure and Guillarmou15, Appendix C] for more details. (We insist on the fact that smoothness is important and this leads to some technical difficulties when working on forms.) We will not specify the dependence on
$\mathscr E$
and in particular for the bundle of forms in the kernel of the contraction, see [Reference Dyatlov, Faure and Guillarmou15, Appendix C] for more details. (We insist on the fact that smoothness is important and this leads to some technical difficulties when working on forms.) We will not specify the dependence on
![]() $\mathscr E$
in the rest of the paper.
$\mathscr E$
in the rest of the paper.
We sum up at the end of the subsection the characterization of generalized eigenfunctions: the resonant states.
A complex number
![]() $\unicode{x3bb} _0$
is a Ruelle resonance if and only if there exists a distribution
$\unicode{x3bb} _0$
is a Ruelle resonance if and only if there exists a distribution
![]() $u\in \mathcal D'(\mathcal M)$
with wavefront set contained in
$u\in \mathcal D'(\mathcal M)$
with wavefront set contained in
![]() $E_u^{*}$
(see for instance [Reference Dyatlov and Zworski16, Lemma 5.1]) such that
$E_u^{*}$
(see for instance [Reference Dyatlov and Zworski16, Lemma 5.1]) such that
![]() $(\mathbf P -\unicode{x3bb} _0)u=0$
, and we will then say that u is a resonant state. We will sometimes write
$(\mathbf P -\unicode{x3bb} _0)u=0$
, and we will then say that u is a resonant state. We will sometimes write
![]() $\mathrm {Res}$
as the set of Ruelle resonances and
$\mathrm {Res}$
as the set of Ruelle resonances and
![]() $\mathrm {Res}_{\unicode{x3bb} _0}$
as the set of resonant states associated to
$\mathrm {Res}_{\unicode{x3bb} _0}$
as the set of resonant states associated to
![]() $\unicode{x3bb} _0$
:
$\unicode{x3bb} _0$
:
We have a corresponding version for the co-resonant states (defined in the next subsection). The wavefront set condition then becomes
![]() $\mathrm {WF}(u)\subset E_s^{*}$
and this will be the version of the proposition that we will use in the proof of Theorem 3.1.
$\mathrm {WF}(u)\subset E_s^{*}$
and this will be the version of the proposition that we will use in the proof of Theorem 3.1.
We finish the subsection by discussing generalized resonant states and the presence of Jordan blocks. More precisely, if we consider the meromorphic extension
![]() $R_+(\unicode{x3bb} )$
constructed in Theorem 2.1, then
$R_+(\unicode{x3bb} )$
constructed in Theorem 2.1, then
![]() $\unicode{x3bb} _0\in \mathrm {Res}$
if and only if
$\unicode{x3bb} _0\in \mathrm {Res}$
if and only if
![]() $\unicode{x3bb} _0$
is a pole of the meromorphic extension. In this case, the spectral projector at
$\unicode{x3bb} _0$
is a pole of the meromorphic extension. In this case, the spectral projector at
![]() $\unicode{x3bb} _0$
is
$\unicode{x3bb} _0$
is
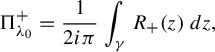 $$ \begin{align*} \Pi^{+}_{\unicode{x3bb}_0}=\frac{1}{2i\pi}\int_{\gamma}R_+(z)\,dz, \end{align*} $$
$$ \begin{align*} \Pi^{+}_{\unicode{x3bb}_0}=\frac{1}{2i\pi}\int_{\gamma}R_+(z)\,dz, \end{align*} $$
where
![]() $\gamma $
is a small loop around
$\gamma $
is a small loop around
![]() $\unicode{x3bb} _0$
. Moreover, we can use the analytic Fredholm theorem to deduce that the resolvent has the following expansion:
$\unicode{x3bb} _0$
. Moreover, we can use the analytic Fredholm theorem to deduce that the resolvent has the following expansion:
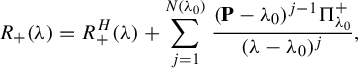 $$ \begin{align*}R_+(\unicode{x3bb})=R_+^H(\unicode{x3bb})+\sum_{j=1}^{N(\unicode{x3bb}_0)}\frac{(\mathbf{P} -\unicode{x3bb}_0)^{j-1}\Pi_{\unicode{x3bb}_0}^+}{(\unicode{x3bb}-\unicode{x3bb}_0)^j}, \end{align*} $$
$$ \begin{align*}R_+(\unicode{x3bb})=R_+^H(\unicode{x3bb})+\sum_{j=1}^{N(\unicode{x3bb}_0)}\frac{(\mathbf{P} -\unicode{x3bb}_0)^{j-1}\Pi_{\unicode{x3bb}_0}^+}{(\unicode{x3bb}-\unicode{x3bb}_0)^j}, \end{align*} $$
where
![]() $R_+^H(\unicode{x3bb} )$
is the holomorphic part near
$R_+^H(\unicode{x3bb} )$
is the holomorphic part near
![]() $\unicode{x3bb} _0$
. The generalized resonant states are
$\unicode{x3bb} _0$
. The generalized resonant states are
Remark 2.2. We will say that the Ruelle resonance
![]() $\unicode{x3bb} _0$
has no Jordan block if
$\unicode{x3bb} _0$
has no Jordan block if
![]() $\mathrm {Res}_{\unicode{x3bb} _0,\infty }=\mathrm {Res}_{\unicode{x3bb} _0}$
. Note that if
$\mathrm {Res}_{\unicode{x3bb} _0,\infty }=\mathrm {Res}_{\unicode{x3bb} _0}$
. Note that if
![]() $N(\unicode{x3bb} _0)=1$
, i.e., the resolvent has a pole of order at most
$N(\unicode{x3bb} _0)=1$
, i.e., the resolvent has a pole of order at most
![]() $1$
, then there is no Jordan block. This will be used in Lemmas 3.5 and 4.2 to show that resonances on the critical axes have no Jordan blocks.
$1$
, then there is no Jordan block. This will be used in Lemmas 3.5 and 4.2 to show that resonances on the critical axes have no Jordan blocks.
2.4 Equilibrium states from dimension theory
In this section, we recall Climenhaga’s construction from [Reference Climenhaga10] of leaf measures
![]() $m^u_V$
and
$m^u_V$
and
![]() $m^s_V$
using dimension theory.
$m^s_V$
using dimension theory.
There are two main ways equilibrium states are defined. The first one is through the use of Markov partitions and the second one is via the use of the specification property. A third approach is given by dimension theory: the goal is to generalize the idea of Haussdorff dimension and Haussdorff measure to a more dynamical setting. We recall the definition of the Haussdorff dimension for a metric space
![]() $(X,\delta )$
. For
$(X,\delta )$
. For
![]() $d\geq 0$
and
$d\geq 0$
and
![]() $\epsilon>0$
, define the d-dimensional Haussdorff measure by
$\epsilon>0$
, define the d-dimensional Haussdorff measure by
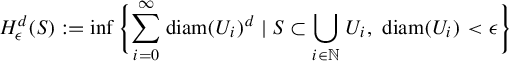 $$ \begin{align*}H^d_{\epsilon}(S):=\inf \bigg\{\!\sum_{i=0}^{\infty} \mathrm{diam}(U_i)^d \mid S\subset \bigcup_{i\in \mathbb N}U_i, \ \mathrm{diam}(U_i)<\epsilon\bigg\}\end{align*} $$
$$ \begin{align*}H^d_{\epsilon}(S):=\inf \bigg\{\!\sum_{i=0}^{\infty} \mathrm{diam}(U_i)^d \mid S\subset \bigcup_{i\in \mathbb N}U_i, \ \mathrm{diam}(U_i)<\epsilon\bigg\}\end{align*} $$
for any subset S and where the infimum is taken over all countable covering of sets
![]() $U_i$
with diameter less than
$U_i$
with diameter less than
![]() $\epsilon $
. We define an outer measure by taking
$\epsilon $
. We define an outer measure by taking
We then define the Haussdorff dimension of X to be
The idea of Climenhaga, Pesin, and Zelerowicz (already present in essence in [Reference Hamenstädt22, Reference Hasselblatt24], where the case of the measure of maximal entropy was treated) was to replace the sets with small diameters by more dynamical objects, namely, coverings should be made of Bowen balls (defined below) and we should let time
![]() $t\to +\infty $
.
$t\to +\infty $
.
Let
![]() $\delta _0>0$
be the size of the local (un)stable manifolds, then fix thereafter
$\delta _0>0$
be the size of the local (un)stable manifolds, then fix thereafter
![]() $\delta \in ]0,\delta _0[$
and define
$\delta \in ]0,\delta _0[$
and define
![]() $\mathcal W^{\bullet }(x,\delta ):=B(x,\delta )\cap \mathcal W^{\bullet }(x)$
, where
$\mathcal W^{\bullet }(x,\delta ):=B(x,\delta )\cap \mathcal W^{\bullet }(x)$
, where
![]() $\bullet =u,s,ws,wu$
. We will not always specify in the rest of the paper the dependence in
$\bullet =u,s,ws,wu$
. We will not always specify in the rest of the paper the dependence in
![]() $\delta $
if it is not relevant to the argument.
$\delta $
if it is not relevant to the argument.
Let
![]() $x\in \mathcal M$
, consider
$x\in \mathcal M$
, consider
![]() $Z\subset \mathcal W^u(x,\delta )$
. Define, for
$Z\subset \mathcal W^u(x,\delta )$
. Define, for
![]() $T>0$
,
$T>0$
,
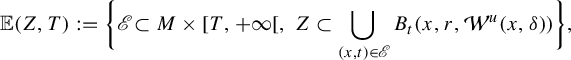 $$ \begin{align*} \mathbb E(Z,T):=\bigg\{\mathscr E \subset M\times [T,+\infty[, \ Z\subset \bigcup_{(x,t)\in \mathscr E}B_t(x,r, \mathcal W^u(x,\delta))\bigg\}, \end{align*} $$
$$ \begin{align*} \mathbb E(Z,T):=\bigg\{\mathscr E \subset M\times [T,+\infty[, \ Z\subset \bigcup_{(x,t)\in \mathscr E}B_t(x,r, \mathcal W^u(x,\delta))\bigg\}, \end{align*} $$
where
![]() $B_t(x,r, \mathcal W^u(x,\delta ))=\{y\in W^u(x,\delta )\mid \max _{[0,t]}d_{W^u(x,\delta )}(\varphi _s x,\varphi _s y)<r\}.$
Let
$B_t(x,r, \mathcal W^u(x,\delta ))=\{y\in W^u(x,\delta )\mid \max _{[0,t]}d_{W^u(x,\delta )}(\varphi _s x,\varphi _s y)<r\}.$
Let
![]() ${\alpha \in {\mathbb R}}$
, then we define a measure
${\alpha \in {\mathbb R}}$
, then we define a measure
![]() $m^{\alpha }_{{\mathcal W}^u(x,\delta )}=m^{\alpha }$
by putting
$m^{\alpha }_{{\mathcal W}^u(x,\delta )}=m^{\alpha }$
by putting
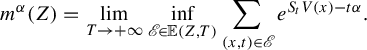 $$ \begin{align*}m^{\alpha}(Z)=\lim_{T\to+\infty}\inf_{\mathscr E\in \mathbb E(Z,T)}\sum_{ (x,t)\in \mathscr E}e^{S_tV(x)-t\alpha}. \end{align*} $$
$$ \begin{align*}m^{\alpha}(Z)=\lim_{T\to+\infty}\inf_{\mathscr E\in \mathbb E(Z,T)}\sum_{ (x,t)\in \mathscr E}e^{S_tV(x)-t\alpha}. \end{align*} $$
We then retrieve the Carathéodory dimension as a threshold just like in the case of the Haussdorff measure, this is a result due to Pesin, see [Reference Pesin32, Propositions 1.1 and 1.2]. We have, moreover, in this case that the measure for
![]() $\alpha =\alpha _C$
defines a Borel measure, see [Reference Climenhaga10, Lemma 2.14].
$\alpha =\alpha _C$
defines a Borel measure, see [Reference Climenhaga10, Lemma 2.14].
The measure
![]() $m^{\alpha }$
defined above is an outer measure for any
$m^{\alpha }$
defined above is an outer measure for any
![]() $\alpha \in \mathbb R$
and
$\alpha \in \mathbb R$
and
Moreover,
![]() $m^{P(V)}$
is a Borel measure, denoted by
$m^{P(V)}$
is a Borel measure, denoted by
![]() $m^u_{x}$
and called the leaf measure. It satisfies
$m^u_{x}$
and called the leaf measure. It satisfies
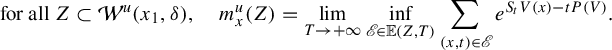 $$ \begin{align} \text{for all } Z \subset \mathcal W^u(x_1,\delta),\quad m^u_x(Z)=\lim_{T\to+\infty}\inf_{\mathscr E\in \mathbb E(Z,T)}\sum_{ (x,t)\in \mathscr E}e^{S_tV(x)-tP(V)}. \end{align} $$
$$ \begin{align} \text{for all } Z \subset \mathcal W^u(x_1,\delta),\quad m^u_x(Z)=\lim_{T\to+\infty}\inf_{\mathscr E\in \mathbb E(Z,T)}\sum_{ (x,t)\in \mathscr E}e^{S_tV(x)-tP(V)}. \end{align} $$
Up until now, we have defined a system of (unstable) leaf measures
![]() $\{m^u_x\mid x\in \mathcal M\}$
satisfying the two following conditions.
$\{m^u_x\mid x\in \mathcal M\}$
satisfying the two following conditions.
-
• Support: each measure
 $m^u_x$
is supported in
$m^u_x$
is supported in
 $\mathcal W^u(x,\delta )$
.
$\mathcal W^u(x,\delta )$
. -
• Compatibility: if
 $Z\subset \mathcal W^u(x_1,\delta )\cap \mathcal W^u(x_2,\delta )$
is a Borel set, then the two measures agree, i.e.,
$Z\subset \mathcal W^u(x_1,\delta )\cap \mathcal W^u(x_2,\delta )$
is a Borel set, then the two measures agree, i.e.,
 $m^u_{x_1}(Z)=m^u_{x_2}(Z)$
.
$m^u_{x_1}(Z)=m^u_{x_2}(Z)$
.
The set of measures defined in equation (29) has actually two more important properties: it is
![]() $\varphi _t$
-conformal and behaves naturally with holonomies (see [Reference Climenhaga10, Theorem 3.4]).
$\varphi _t$
-conformal and behaves naturally with holonomies (see [Reference Climenhaga10, Theorem 3.4]).
The system of (unstable) leaf measures
![]() $\{m^u_x\mid x\in \mathcal M\}$
defined in equation (29) is
$\{m^u_x\mid x\in \mathcal M\}$
defined in equation (29) is
![]() $\varphi _t$
-conformal, namely, for any
$\varphi _t$
-conformal, namely, for any
![]() $x\in \mathcal M$
and
$x\in \mathcal M$
and
![]() $t\in \mathbb R$
, the measures
$t\in \mathbb R$
, the measures
![]() $(\varphi _t)_*m^u_x$
and
$(\varphi _t)_*m^u_x$
and
![]() $m^u_{\varphi _t x}$
are equivalent and more precisely,
$m^u_{\varphi _t x}$
are equivalent and more precisely,
In terms of Radon–Nikodym derivatives, we have
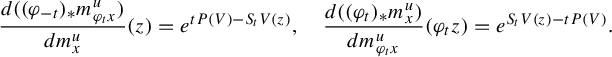 $$ \begin{align} \frac{d((\varphi_{-t})_*m^u_{\varphi_t x})}{dm^u_x}(z)=e^{tP(V)-S_tV(z)},\quad \frac{d((\varphi_{t})_*m^u_{ x})}{dm^u_{\varphi _tx}}(\varphi_t z)=e^{S_tV(z)-tP(V)}. \end{align} $$
$$ \begin{align} \frac{d((\varphi_{-t})_*m^u_{\varphi_t x})}{dm^u_x}(z)=e^{tP(V)-S_tV(z)},\quad \frac{d((\varphi_{t})_*m^u_{ x})}{dm^u_{\varphi _tx}}(\varphi_t z)=e^{S_tV(z)-tP(V)}. \end{align} $$
We define the notion of holonomy between (weak-un)stable leaves.
Given
![]() $\mathcal W^u(x_1,\delta ),\mathcal W^u(x_2,\delta )$
for
$\mathcal W^u(x_1,\delta ),\mathcal W^u(x_2,\delta )$
for
![]() $x_1,x_2\in \mathcal M$
, a weak-stable
$x_1,x_2\in \mathcal M$
, a weak-stable
![]() $\delta $
-holonomy between
$\delta $
-holonomy between
![]() $\mathcal W^u(x_1,\delta )$
and
$\mathcal W^u(x_1,\delta )$
and
![]() $\mathcal W^u(x_2,\delta )$
is a homeomorphism
$\mathcal W^u(x_2,\delta )$
is a homeomorphism
![]() $\pi :\mathcal W^u(x_1,\delta )\to \mathcal W^u(x_2,\delta )$
such that
$\pi :\mathcal W^u(x_1,\delta )\to \mathcal W^u(x_2,\delta )$
such that
![]() $\pi (z)\in \mathcal W^{ws}(z,\delta )$
for all
$\pi (z)\in \mathcal W^{ws}(z,\delta )$
for all
![]() $z\in \mathcal W^u(x_1,\delta )$
.
$z\in \mathcal W^u(x_1,\delta )$
.
To conclude, we give the change of variable formula for holonomies. We first introduce a useful function. Let
![]() $\delta _0>0$
be small enough, given
$\delta _0>0$
be small enough, given
![]() $x\in \mathcal M$
and
$x\in \mathcal M$
and
![]() $y\in \mathcal W^{ws}(x,\delta _0)$
, define
$y\in \mathcal W^{ws}(x,\delta _0)$
, define
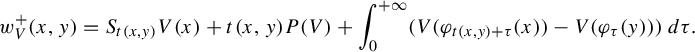 $$ \begin{align} w_V^+(x,y)=S_{t(x,y)}V(x)+t(x,y)P(V)+\int_0^{+\infty}(V(\varphi_{t(x,y)+\tau}(x))-V(\varphi_{\tau}(y)))\,d\tau. \end{align} $$
$$ \begin{align} w_V^+(x,y)=S_{t(x,y)}V(x)+t(x,y)P(V)+\int_0^{+\infty}(V(\varphi_{t(x,y)+\tau}(x))-V(\varphi_{\tau}(y)))\,d\tau. \end{align} $$
Here,
![]() $t(x,y)$
is the Bowen time and the integral converges because
$t(x,y)$
is the Bowen time and the integral converges because
![]() $d(\varphi _{t+\tau }x,\varphi _{\tau }y)\to 0$
exponentially fast and V is Hölder continuous.
$d(\varphi _{t+\tau }x,\varphi _{\tau }y)\to 0$
exponentially fast and V is Hölder continuous.
We define for
![]() $x\in \mathcal M$
and
$x\in \mathcal M$
and
![]() $y\in \mathcal W^{wu}(x,\delta _0)$
the quantity
$y\in \mathcal W^{wu}(x,\delta _0)$
the quantity
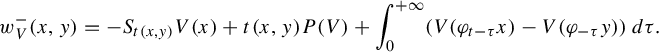 $$ \begin{align*}w_V^-(x,y)=-S_{t(x,y)}V(x)+t(x,y)P(V)+\int_0^{+\infty}(V(\varphi_{t-\tau}x)-V(\varphi_{-\tau}y))\,d\tau. \end{align*} $$
$$ \begin{align*}w_V^-(x,y)=-S_{t(x,y)}V(x)+t(x,y)P(V)+\int_0^{+\infty}(V(\varphi_{t-\tau}x)-V(\varphi_{-\tau}y))\,d\tau. \end{align*} $$
We note that we have the following special values:
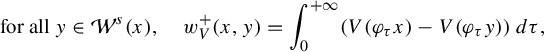 $$ \begin{align*} \text{for all } y\in \mathcal W^s(x), \quad w^+_V(x,y)=\int_0^{+\infty}(V(\varphi_{\tau}x)-V(\varphi_{\tau}y))\,d\tau, \end{align*} $$
$$ \begin{align*} \text{for all } y\in \mathcal W^s(x), \quad w^+_V(x,y)=\int_0^{+\infty}(V(\varphi_{\tau}x)-V(\varphi_{\tau}y))\,d\tau, \end{align*} $$
as well as
Finally, we have the cocycle relation
The holonomy we will mostly be interested in will be given by
![]() $\pi : \mathcal W^u(q,\delta )\to \mathcal W^u(p,\delta ), \pi (x):=[x,p]$
and we can now state the second change of variable theorem, see [Reference Climenhaga10, Theorem 3.4] for more details.
$\pi : \mathcal W^u(q,\delta )\to \mathcal W^u(p,\delta ), \pi (x):=[x,p]$
and we can now state the second change of variable theorem, see [Reference Climenhaga10, Theorem 3.4] for more details.
Consider the system of (unstable) leaf measures
![]() $\{m^u_x\mid x\in \mathcal M\}$
defined in equation (29). Let
$\{m^u_x\mid x\in \mathcal M\}$
defined in equation (29). Let
![]() $\mathcal W^u(x_1,\delta ),\mathcal W^u(x_2,\delta )$
for
$\mathcal W^u(x_1,\delta ),\mathcal W^u(x_2,\delta )$
for
![]() $x_1,x_2\in \mathcal M$
and let
$x_1,x_2\in \mathcal M$
and let
![]() $\pi :\mathcal W^u(x_1,\delta )\to \mathcal W^u(x_2,\delta )$
be a weak-stable
$\pi :\mathcal W^u(x_1,\delta )\to \mathcal W^u(x_2,\delta )$
be a weak-stable
![]() $\delta _0$
holonomy. Then, the measures
$\delta _0$
holonomy. Then, the measures
![]() $\pi _*m_{x_1}^u$
and
$\pi _*m_{x_1}^u$
and
![]() $m_{x_2}^u$
are equivalent, and we have
$m_{x_2}^u$
are equivalent, and we have
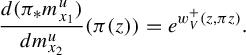 $$ \begin{align} \frac{d(\pi_*m^u_{x_1})}{dm^u_{x_2}}(\pi(z))=e^{w^+_V(z,\pi z)}. \end{align} $$
$$ \begin{align} \frac{d(\pi_*m^u_{x_1})}{dm^u_{x_2}}(\pi(z))=e^{w^+_V(z,\pi z)}. \end{align} $$
3 Resolvent acting on functions
In this section, we study the action of
![]() $\mathbf {P}$
on
$\mathbf {P}$
on
![]() $0$
-forms. The following proofs could all be written in the formalism of currents as it is done in §4 for the
$0$
-forms. The following proofs could all be written in the formalism of currents as it is done in §4 for the
![]() $d_s$
-forms, but we remark that by fixing a smooth volume form, one can reduce to studying the action of
$d_s$
-forms, but we remark that by fixing a smooth volume form, one can reduce to studying the action of
![]() $\mathbf {P}$
on function, which we will do here. The goal is to locate the critical axis, show that it is given by
$\mathbf {P}$
on function, which we will do here. The goal is to locate the critical axis, show that it is given by
![]() $\{\mathrm {Re}(\unicode{x3bb} )=P(V+J^u)\}$
, and to study the co-resonant states associated to resonances on this axis.
$\{\mathrm {Re}(\unicode{x3bb} )=P(V+J^u)\}$
, and to study the co-resonant states associated to resonances on this axis.
3.1 Construction of the co-resonant state
We first prove that
![]() $P(V+J^u)$
is indeed a resonance, called the first resonance. In the case of a null potential (
$P(V+J^u)$
is indeed a resonance, called the first resonance. In the case of a null potential (
![]() $V=0$
), this is trivial as constant functions lie trivially in the kernel of the flow. In this case, the equilibrium state (which is usually referred to as the SRB measure) can be identified as the co-resonant state for the Ruelle resonance
$V=0$
), this is trivial as constant functions lie trivially in the kernel of the flow. In this case, the equilibrium state (which is usually referred to as the SRB measure) can be identified as the co-resonant state for the Ruelle resonance
![]() $0$
.
$0$
.
Following §2.3, we can define Ruelle resonances for the
![]() $L^2$
-adjoint
$L^2$
-adjoint
![]() $\mathbf {P}^{*}=X+V-\mathrm {div}_{\mathrm {vol}}(X)$
. The resonant states for
$\mathbf {P}^{*}=X+V-\mathrm {div}_{\mathrm {vol}}(X)$
. The resonant states for
![]() $\mathbf {P}^{*}$
are referred to as co-resonant states for
$\mathbf {P}^{*}$
are referred to as co-resonant states for
![]() $\mathbf {P}$
and their span has the same dimension as the span of the resonant states. Equivalently, we can define the adjoint by duality, using relation (21), as
$\mathbf {P}$
and their span has the same dimension as the span of the resonant states. Equivalently, we can define the adjoint by duality, using relation (21), as
from which we can define an unbounded operator
Now, a direct adaptation of [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Lemma 5.3] yields the following lemma.
Lemma 3.1. (Co-resonant states)
Let
![]() $\unicode{x3bb} \in \mathbb C$
, then
$\unicode{x3bb} \in \mathbb C$
, then
![]() $\unicode{x3bb} $
is a Ruelle resonance for
$\unicode{x3bb} $
is a Ruelle resonance for
![]() $\mathbf {P}$
if and only if
$\mathbf {P}$
if and only if
![]() $\overline {\unicode{x3bb} }$
is a Ruelle resonance for
$\overline {\unicode{x3bb} }$
is a Ruelle resonance for
![]() $\mathbf {P}^{*}$
. In this case, the space of resonant and co-resonant states have the same dimension m. If we consider
$\mathbf {P}^{*}$
. In this case, the space of resonant and co-resonant states have the same dimension m. If we consider
![]() $u_1,\ldots , u_m\in \mathcal D^{\prime }_{E_u^{*}}(\mathcal M):=\{u\in \mathcal D'\mid \mathrm {WF}(u)\subset E_u^{*}\}$
and
$u_1,\ldots , u_m\in \mathcal D^{\prime }_{E_u^{*}}(\mathcal M):=\{u\in \mathcal D'\mid \mathrm {WF}(u)\subset E_u^{*}\}$
and
![]() $v_1,\ldots , v_m\in \mathcal D^{\prime }_{E_s^{*}}(\mathcal M):=\{u\in \mathcal D'\mid \mathrm {WF}(u)\subset E_s^{*}\}$
as two bases of the resonant states for
$v_1,\ldots , v_m\in \mathcal D^{\prime }_{E_s^{*}}(\mathcal M):=\{u\in \mathcal D'\mid \mathrm {WF}(u)\subset E_s^{*}\}$
as two bases of the resonant states for
![]() $\mathbf {P}$
and
$\mathbf {P}$
and
![]() $\mathbf {P}^{*}$
, respectively, satisfying
$\mathbf {P}^{*}$
, respectively, satisfying
![]() $( u_i,v_j)=\delta _{i,j}$
, then the projector
$( u_i,v_j)=\delta _{i,j}$
, then the projector
![]() $\Pi _0(\unicode{x3bb} )$
on the space of resonant states for the resonance
$\Pi _0(\unicode{x3bb} )$
on the space of resonant states for the resonance
![]() $\unicode{x3bb} $
is given by
$\unicode{x3bb} $
is given by
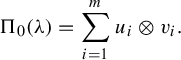 $$ \begin{align} \Pi_0(\unicode{x3bb})=\sum_{i=1}^mu_i\otimes v_i. \end{align} $$
$$ \begin{align} \Pi_0(\unicode{x3bb})=\sum_{i=1}^mu_i\otimes v_i. \end{align} $$
In [Reference Climenhaga10, Theorem 3.10], Climenhaga gives a local product construction of the equilibrium state. For this, let us first notice that Climenhaga’s construction is still valid when swapping the unstable and stable foliations.
We can thus define a system of stable leaf measures
![]() $\{m^s_x\mid x\in \mathcal M\}$
which is compatible and supported in
$\{m^s_x\mid x\in \mathcal M\}$
which is compatible and supported in
![]() $\mathcal W^s(x)$
. Moreover,
$\mathcal W^s(x)$
. Moreover,
![]() $m^s_x$
is defined using equation (29), but using backward Bowen-balls, see [Reference Climenhaga10, §3.3] for details. The set
$m^s_x$
is defined using equation (29), but using backward Bowen-balls, see [Reference Climenhaga10, §3.3] for details. The set
![]() $\{m^s_x\mid x\in \mathcal M\}$
is
$\{m^s_x\mid x\in \mathcal M\}$
is
![]() $\varphi _t$
-conformal in the sense of equation (30) and the change of variable by holonomy is the one explicated in equation (35) but with
$\varphi _t$
-conformal in the sense of equation (30) and the change of variable by holonomy is the one explicated in equation (35) but with
![]() $w^+$
replaced by
$w^+$
replaced by
![]() $w^-$
.
$w^-$
.
We can then extend the leaf measures to the weak (un)stable foliations
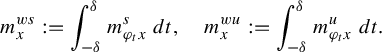 $$ \begin{align} m^{ws}_{x}:=\int_{-\delta}^{\delta}m^s_{\varphi_t x}\,dt,\quad m^{wu}_{x}:=\int_{-\delta}^{\delta}m^u_{\varphi_t x}\,dt. \end{align} $$
$$ \begin{align} m^{ws}_{x}:=\int_{-\delta}^{\delta}m^s_{\varphi_t x}\,dt,\quad m^{wu}_{x}:=\int_{-\delta}^{\delta}m^u_{\varphi_t x}\,dt. \end{align} $$
To state the main result of this subsection, we introduce further notation,
where
![]() $R_q$
and
$R_q$
and
![]() $\Psi _q$
are defined in equation (16). Observe that
$\Psi _q$
are defined in equation (16). Observe that
We adapt the product construction of Climenhaga [Reference Climenhaga10, Theorem 3.10] to obtain the following local construction of the co-resonant state. In the following, we add an additional index W to denote the leaf measures constructed using equation (29) from the Hölder continuous potential W. For any
![]() $q\in \mathcal M$
, we define three measures on
$q\in \mathcal M$
, we define three measures on
![]() $R_q$
by putting, for a Borel set
$R_q$
by putting, for a Borel set
![]() $Z\subset R_q$
,
$Z\subset R_q$
,
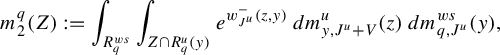 $$ \begin{align} m_2^q(Z)&:=\int_{R^{ws}_q}\int_{Z\cap R^u_q(y)} e^{w^-_{J^u}(z,y)}\,dm^u_{y,J^u+V}(z)\,dm^{ws}_{q, J^u}(y),\qquad\quad\qquad \end{align} $$
$$ \begin{align} m_2^q(Z)&:=\int_{R^{ws}_q}\int_{Z\cap R^u_q(y)} e^{w^-_{J^u}(z,y)}\,dm^u_{y,J^u+V}(z)\,dm^{ws}_{q, J^u}(y),\qquad\quad\qquad \end{align} $$
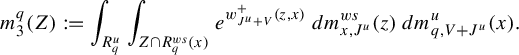 $$ \begin{align} m_3^q(Z)&:=\int_{R^{u}_q}\int_{Z\cap R^{ws}_q(x)} e^{w^+_{J^u+V}(z,x)}\,dm^{ws}_{x,J^u}(z)\,dm^u_{q,V+J^u}(x).\qquad\qquad \end{align} $$
$$ \begin{align} m_3^q(Z)&:=\int_{R^{u}_q}\int_{Z\cap R^{ws}_q(x)} e^{w^+_{J^u+V}(z,x)}\,dm^{ws}_{x,J^u}(z)\,dm^u_{q,V+J^u}(x).\qquad\qquad \end{align} $$
Theorem 3.1. (Construction of the co-resonant state)
For any
![]() $q\in \mathcal M$
, the three measures
$q\in \mathcal M$
, the three measures
![]() $m_1^q,m_2^q$
, and
$m_1^q,m_2^q$
, and
![]() $m_3^q$
coincide, and there is a unique non-zero and finite Borel measure
$m_3^q$
coincide, and there is a unique non-zero and finite Borel measure
![]() $\nu $
on
$\nu $
on
![]() $\mathcal M$
such that
$\mathcal M$
such that
![]() $\text {for all } Z\subset R_q$
, one has
$\text {for all } Z\subset R_q$
, one has
![]() $\nu (Z)=m_1(Z)$
. This Borel measure satisfies
$\nu (Z)=m_1(Z)$
. This Borel measure satisfies
and is therefore a co-resonant state. In other words,
![]() $P(V+J^u)$
is a Ruelle resonance.
$P(V+J^u)$
is a Ruelle resonance.
Remark 3.1. Climenhaga’s original construction is obtained by taking the two potentials to be equal, in other words, all leaf measures are constructed using V and the resulting Borel measure is a non-zero multiple of the equilibrium state
![]() $\mu _V$
. We observe that when
$\mu _V$
. We observe that when
![]() $V=0$
, both constructions coincide and we retrieve the known fact that the SRB measure is the co-resonant state in this case. Of course, by taking the adjoint, we obtain a construction of a resonant state
$V=0$
, both constructions coincide and we retrieve the known fact that the SRB measure is the co-resonant state in this case. Of course, by taking the adjoint, we obtain a construction of a resonant state
![]() $\eta $
.
$\eta $
.
Proof. We mostly follow the strategy of the proof of [Reference Climenhaga10, Theorem 10], while only changing the necessary details. We first prove that the three formulas indeed agree and define the same local measure. Starting from a measurable function
![]() $\zeta : \mathcal W^u(q,\delta )\times \mathcal W^{ws}(q,\delta )\to ]0,+\infty [$
, one sees that
$\zeta : \mathcal W^u(q,\delta )\times \mathcal W^{ws}(q,\delta )\to ]0,+\infty [$
, one sees that
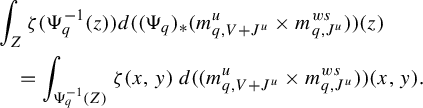 $$ \begin{align*} &\int_Z \zeta(\Psi^{-1}_q(z))d((\Psi_q)_*(m^u_{q,V+J^u}\times m^{ws}_{q, J^u}))(z)\\ &\quad=\int_{\Psi_q^{-1}(Z)}\zeta(x,y)\,d((m^u_{q,V+J^u}\times m^{ws}_{q, J^u}))(x,y). \end{align*} $$
$$ \begin{align*} &\int_Z \zeta(\Psi^{-1}_q(z))d((\Psi_q)_*(m^u_{q,V+J^u}\times m^{ws}_{q, J^u}))(z)\\ &\quad=\int_{\Psi_q^{-1}(Z)}\zeta(x,y)\,d((m^u_{q,V+J^u}\times m^{ws}_{q, J^u}))(x,y). \end{align*} $$
Now, this last expression can be seen to be equal to equation (42), using the change of variable by holonomy in equation (35) with the holonomy
![]() $\pi :\mathcal W^u(q,\delta )\to R^u_q(y), \pi (x)=[x,y]$
and with
$\pi :\mathcal W^u(q,\delta )\to R^u_q(y), \pi (x)=[x,y]$
and with
![]() $\zeta (z):=e^{w^+_{V+J^u}(z,[z,q])+w^-_{J^u}(z,[q,z])}$
.
$\zeta (z):=e^{w^+_{V+J^u}(z,[z,q])+w^-_{J^u}(z,[q,z])}$
.
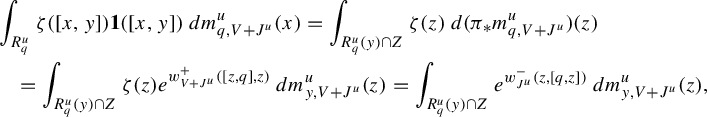 $$ \begin{align*} &\int_{R^u_q}\zeta([x,y])\mathbf{1}([x,y])\,d m^u_{q,V+J^u}(x)=\int_{R^u_q(y)\cap Z}\zeta(z)\,d(\pi_*m^u_{q,V+J^u})(z)\\ &\quad =\int_{R^u_q(y)\cap Z}\zeta(z)e^{w^+_{V+J^u}([z,q],z)}\,dm^u_{y,V+J^u}(z)=\int_{R^u_q(y)\cap Z}e^{w^-_{J^u}(z,[q,z])}\,dm^u_{y,V+J^u}(z), \end{align*} $$
$$ \begin{align*} &\int_{R^u_q}\zeta([x,y])\mathbf{1}([x,y])\,d m^u_{q,V+J^u}(x)=\int_{R^u_q(y)\cap Z}\zeta(z)\,d(\pi_*m^u_{q,V+J^u})(z)\\ &\quad =\int_{R^u_q(y)\cap Z}\zeta(z)e^{w^+_{V+J^u}([z,q],z)}\,dm^u_{y,V+J^u}(z)=\int_{R^u_q(y)\cap Z}e^{w^-_{J^u}(z,[q,z])}\,dm^u_{y,V+J^u}(z), \end{align*} $$
where we used the cocycle relation (34). Similarly, we obtain the equivalent equation (43). Next, we show that the set of local measures
![]() $\{\nu _q\mid q\in \mathcal M\}$
are compatible in the sense that for any Borel set
$\{\nu _q\mid q\in \mathcal M\}$
are compatible in the sense that for any Borel set
![]() $ Z\subset R_q\cap R_p$
, one has
$ Z\subset R_q\cap R_p$
, one has
![]() $ \nu _q(Z)=\nu _p(Z).$
This will then define a global Borel measure. If
$ \nu _q(Z)=\nu _p(Z).$
This will then define a global Borel measure. If
![]() $p\in \mathcal W^{ws}(q,\delta )$
, then we deduce that the above relation follows from equation (42) and the fact that the system measures
$p\in \mathcal W^{ws}(q,\delta )$
, then we deduce that the above relation follows from equation (42) and the fact that the system measures
![]() $\{m^s_x\mid x\in \mathcal M\}$
is compatible on the intersection. Similarly, the relation for
$\{m^s_x\mid x\in \mathcal M\}$
is compatible on the intersection. Similarly, the relation for
![]() $p\in \mathcal W^{u}(q,\delta )$
follows from the compatibility of
$p\in \mathcal W^{u}(q,\delta )$
follows from the compatibility of
![]() $\{m^{ws}_x\mid x\in \mathcal M\}$
and equation (43). The general case then follows from the local product structure. Call
$\{m^{ws}_x\mid x\in \mathcal M\}$
and equation (43). The general case then follows from the local product structure. Call
![]() $\nu $
the global Borel measure we obtain. The fact that
$\nu $
the global Borel measure we obtain. The fact that
![]() $\nu $
is non-zero and finite follows from the analog fact on the local measures
$\nu $
is non-zero and finite follows from the analog fact on the local measures
![]() $\nu _q$
and the compactness of the space
$\nu _q$
and the compactness of the space
![]() $\mathcal M$
. What is left to prove is equation (44). It suffices to show that one has
$\mathcal M$
. What is left to prove is equation (44). It suffices to show that one has
which will clearly imply the first part of equation (44). Because the measure
![]() $\nu $
is constructed from its restrictions, it will be enough to prove that
$\nu $
is constructed from its restrictions, it will be enough to prove that
We now use equation (43) to compute explicitly, using the
![]() $\varphi _t$
-conformality in equation (30):
$\varphi _t$
-conformality in equation (30):
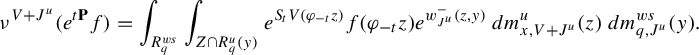 $$ \begin{align*} \nu^{V+J^u}(e^{t\mathbf{P}}f)&=\int_{R^{ws}_q}\int_{Z\cap R^{u}_q(y)}e^{S_tV(\varphi_{-t}z)}f(\varphi_{-t}z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{x, V+J^u}(z)\, dm^{ws}_{q,J^u}(y). \end{align*} $$
$$ \begin{align*} \nu^{V+J^u}(e^{t\mathbf{P}}f)&=\int_{R^{ws}_q}\int_{Z\cap R^{u}_q(y)}e^{S_tV(\varphi_{-t}z)}f(\varphi_{-t}z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{x, V+J^u}(z)\, dm^{ws}_{q,J^u}(y). \end{align*} $$
The cocycle relation (34) gives
![]() $e^{w^-_{J^u}(z,y)}=e^{w^-_{J^u}(z,\varphi _{-t}z)}e^{w^-_{J^u}(\varphi _{-t}z,y)}. $
Using equation (33) to get
$e^{w^-_{J^u}(z,y)}=e^{w^-_{J^u}(z,\varphi _{-t}z)}e^{w^-_{J^u}(\varphi _{-t}z,y)}. $
Using equation (33) to get
![]() $w^+_{J^u}(z,\varphi _{-t}z)=S_{t}J^u(\varphi _{-t}z)$
, this means that
$w^+_{J^u}(z,\varphi _{-t}z)=S_{t}J^u(\varphi _{-t}z)$
, this means that
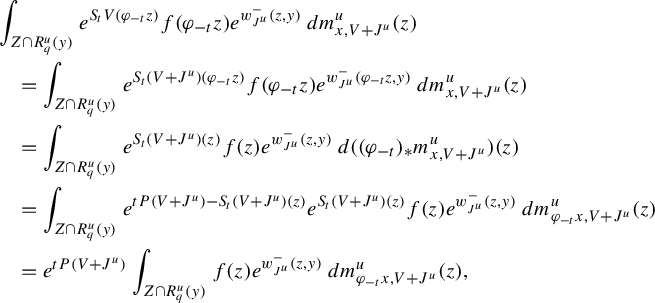 $$ \begin{align*} &\int_{Z\cap R^{u}_q(y)}e^{S_tV(\varphi_{-t}z)}f(\varphi_{-t}z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{x, V+J^u}(z)\\ &\quad = \int_{Z\cap R^{u}_q(y)}e^{S_t(V+J^u)(\varphi_{-t}z)}f(\varphi_{-t}z) e^{w^-_{J^u}(\varphi_{-t}z,y)}\,dm^{u}_{x, V+J^u}(z)\\ &\quad = \int_{Z\cap R^{u}_q(y)}e^{S_t(V+J^u)(z)}f(z) e^{w^-_{J^u}(z,y)}\,d ((\varphi_{-t})_*m^{u}_{x, V+J^u})(z)\\ &\quad = \int_{Z\cap R^{u}_q(y)}e^{tP(V+J^u)-S_t(V+J^u)(z)}e^{S_t(V+J^u)(z)}f(z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{\varphi_{-t}x, V+J^u}(z)\\ &\quad = e^{tP(V+J^u)} \int_{Z\cap R^{u}_q(y)}f(z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{\varphi_{-t}x, V+J^u}(z), \end{align*} $$
$$ \begin{align*} &\int_{Z\cap R^{u}_q(y)}e^{S_tV(\varphi_{-t}z)}f(\varphi_{-t}z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{x, V+J^u}(z)\\ &\quad = \int_{Z\cap R^{u}_q(y)}e^{S_t(V+J^u)(\varphi_{-t}z)}f(\varphi_{-t}z) e^{w^-_{J^u}(\varphi_{-t}z,y)}\,dm^{u}_{x, V+J^u}(z)\\ &\quad = \int_{Z\cap R^{u}_q(y)}e^{S_t(V+J^u)(z)}f(z) e^{w^-_{J^u}(z,y)}\,d ((\varphi_{-t})_*m^{u}_{x, V+J^u})(z)\\ &\quad = \int_{Z\cap R^{u}_q(y)}e^{tP(V+J^u)-S_t(V+J^u)(z)}e^{S_t(V+J^u)(z)}f(z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{\varphi_{-t}x, V+J^u}(z)\\ &\quad = e^{tP(V+J^u)} \int_{Z\cap R^{u}_q(y)}f(z) e^{w^-_{J^u}(z,y)}\,dm^{u}_{\varphi_{-t}x, V+J^u}(z), \end{align*} $$
where we used the
![]() $\varphi _t$
-conformality, see equation (31). This implies equation (45) and thus
$\varphi _t$
-conformality, see equation (31). This implies equation (45) and thus
The last thing we need to do is to bound the wavefront set of the measure
![]() $\nu $
. For this, we will need some regularity result on the conditional measures of the SRB measures and the following adaptation of [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Lemma 2.9].
$\nu $
. For this, we will need some regularity result on the conditional measures of the SRB measures and the following adaptation of [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Lemma 2.9].
Lemma 3.2. The wavefront set of
![]() $\nu $
is included in
$\nu $
is included in
![]() $E_s^{*}$
.
$E_s^{*}$
.
Proof. Consider
![]() $q\in \mathcal M$
and
$q\in \mathcal M$
and
![]() $\xi \notin E_s^{*}(q)$
, and we shall prove that
$\xi \notin E_s^{*}(q)$
, and we shall prove that
![]() $(q,\xi )$
is not in the wavefront set. Choose a phase function S such that
$(q,\xi )$
is not in the wavefront set. Choose a phase function S such that
![]() $d_qS=\xi $
and a cutoff
$d_qS=\xi $
and a cutoff
![]() $\chi $
near q, we then use equation (43) to obtain
$\chi $
near q, we then use equation (43) to obtain
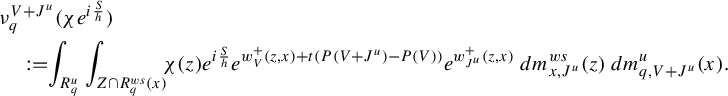 $$ \begin{align*} &\nu^{V+J^u}_q(\chi e^{i\frac Sh})\\ &\quad :=\!\int_{R^{u}_q}\int_{Z\cap R^{ws}_q(x)}\!\! \chi(z)e^{i\frac Sh} e^{w^+_{V}(z,x)+t(P(V+J^u)-P(V))}e^{w^+_{J^u}(z,x)}\,dm^{ws}_{x,J^u}(z)\,dm^u_{q,V+J^u}(x). \end{align*} $$
$$ \begin{align*} &\nu^{V+J^u}_q(\chi e^{i\frac Sh})\\ &\quad :=\!\int_{R^{u}_q}\int_{Z\cap R^{ws}_q(x)}\!\! \chi(z)e^{i\frac Sh} e^{w^+_{V}(z,x)+t(P(V+J^u)-P(V))}e^{w^+_{J^u}(z,x)}\,dm^{ws}_{x,J^u}(z)\,dm^u_{q,V+J^u}(x). \end{align*} $$
Now, we can use [Reference Climenhaga10, Corollary 3.11] to obtain that
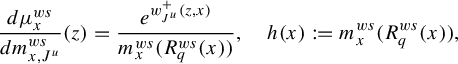 $$ \begin{align*}\frac{d\mu_x^{ws}}{d m^{ws}_{x,J^u}}(z)=\frac{e^{w^+_{J^u}(z,x)}}{m^{ws}_x(R_q^{ws}(x))}, \quad h(x):= m^{ws}_x(R_q^{ws}(x)),\end{align*} $$
$$ \begin{align*}\frac{d\mu_x^{ws}}{d m^{ws}_{x,J^u}}(z)=\frac{e^{w^+_{J^u}(z,x)}}{m^{ws}_x(R_q^{ws}(x))}, \quad h(x):= m^{ws}_x(R_q^{ws}(x)),\end{align*} $$
where
![]() $\mu _x^{ws}$
is the conditional measure of the SRB measure on the weak unstable manifold, in other words,
$\mu _x^{ws}$
is the conditional measure of the SRB measure on the weak unstable manifold, in other words,
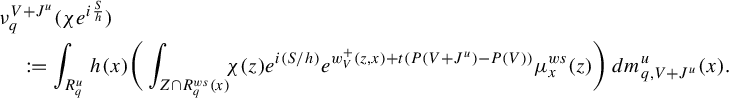 $$ \begin{align*} &\nu^{V+J^u}_q(\chi e^{i\frac Sh})\\ &\quad :=\int_{R^{u}_q}h(x)\bigg(\int_{Z\cap R^{ws}_q(x)}\!\!\chi(z)e^{i(S/h)} e^{w^+_{V}(z,x)+t(P(V+J^u)-P(V))}\mu_x^{ws}(z)\bigg)\,dm^u_{q,V+J^u}(x). \end{align*} $$
$$ \begin{align*} &\nu^{V+J^u}_q(\chi e^{i\frac Sh})\\ &\quad :=\int_{R^{u}_q}h(x)\bigg(\int_{Z\cap R^{ws}_q(x)}\!\!\chi(z)e^{i(S/h)} e^{w^+_{V}(z,x)+t(P(V+J^u)-P(V))}\mu_x^{ws}(z)\bigg)\,dm^u_{q,V+J^u}(x). \end{align*} $$
Now, we use [Reference De La Llave14, Theorem 3.9] to obtain that the density
![]() $\mu _x^{ws}$
is smooth along the leaves
$\mu _x^{ws}$
is smooth along the leaves
![]() $R_q^{ws}(x)$
. By this, we mean that
$R_q^{ws}(x)$
. By this, we mean that
is finite for any k and that the norm depends continuously in x.
From the proof of [Reference De La Llave14, Corollary 4.4], one sees that the smoothness of the potential V implies that
![]() $w_V^+(z,x)$
is smooth along the leaves
$w_V^+(z,x)$
is smooth along the leaves
![]() $R_q^{ws}(x)$
. More precisely, the proof shows that given a function which is smooth along the leaves, the function defined by the last integral in equation (32) is smooth along the leaves, therefore proving that the holonomy factor is smooth along the leaves. (Note that the fact that the unstable Jacobian is smooth along the leaves in the sense above is non-trivial because it is only Hölder continuous in x.)
$R_q^{ws}(x)$
. More precisely, the proof shows that given a function which is smooth along the leaves, the function defined by the last integral in equation (32) is smooth along the leaves, therefore proving that the holonomy factor is smooth along the leaves. (Note that the fact that the unstable Jacobian is smooth along the leaves in the sense above is non-trivial because it is only Hölder continuous in x.)
Using the fact that each leaf is a smooth submanifold, we can perform integration by parts (in z) to show that the inner integral is
![]() $O(h^{\infty })$
as long as
$O(h^{\infty })$
as long as
![]() $dS_{|R_w^{ws}}(x)$
does not vanish. However,
$dS_{|R_w^{ws}}(x)$
does not vanish. However,
![]() $\xi \notin E_s^{*}$
, so this can be ensured locally near p. This proves that
$\xi \notin E_s^{*}$
, so this can be ensured locally near p. This proves that
![]() $\xi \notin E_s^{*}$
and we have thus shown that
$\xi \notin E_s^{*}$
and we have thus shown that
![]() $\mathrm {WF}(\nu )\subset E_s^{*}$
.
$\mathrm {WF}(\nu )\subset E_s^{*}$
.
We can now finish the proof of Theorem 3.1. For this, we use the characterization in equation (26) to deduce that
![]() $\nu $
is indeed a co-resonant state, i.e.,
$\nu $
is indeed a co-resonant state, i.e.,
![]() $P(V+J^u)$
is a Ruelle resonance.
$P(V+J^u)$
is a Ruelle resonance.
3.2 Critical axis
In this subsection, we prove that the set of Ruelle resonances is contained in the half-plane
![]() $\{\unicode{x3bb} \mid \mathrm {Re}(\unicode{x3bb} )\leq P(V+J^u)\}$
. The case
$\{\unicode{x3bb} \mid \mathrm {Re}(\unicode{x3bb} )\leq P(V+J^u)\}$
. The case
![]() $V=0$
is enlightening; in this case, the critical axis is the imaginary axis. No resonance has positive real part, indeed, in the case of a volume preserving Anosov flow, this follows directly from Theorem 2.1, while in the general case, it follows from the general bound
$V=0$
is enlightening; in this case, the critical axis is the imaginary axis. No resonance has positive real part, indeed, in the case of a volume preserving Anosov flow, this follows directly from Theorem 2.1, while in the general case, it follows from the general bound
![]() $\|e^{-Xt}f\|_{L^{\infty }}\leq \|f\|_{L^{\infty }}$
, see [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Corollary 4.16]. We insist on the fact that the functional space
$\|e^{-Xt}f\|_{L^{\infty }}\leq \|f\|_{L^{\infty }}$
, see [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Corollary 4.16]. We insist on the fact that the functional space
![]() $L^{\infty }$
is not really part of the
$L^{\infty }$
is not really part of the
![]() $L^2$
-anisotropic Sobolev spaces scale and, thus, this part of the proof needs the introduction of some ‘finer’ measure theory. The goal of this subsection is thus to construct, using the co-resonant state
$L^2$
-anisotropic Sobolev spaces scale and, thus, this part of the proof needs the introduction of some ‘finer’ measure theory. The goal of this subsection is thus to construct, using the co-resonant state
![]() $\nu $
defined in Theorem 3.1, a norm
$\nu $
defined in Theorem 3.1, a norm
![]() $\|.\|_V$
such that
$\|.\|_V$
such that
Lemma 3.3. Let
![]() $\nu $
be as in Theorem 3.1, for
$\nu $
be as in Theorem 3.1, for
![]() $f\in C^{\infty }(\mathcal M)$
, define
$f\in C^{\infty }(\mathcal M)$
, define
Then, this defines a norm on
![]() $C^{\infty }(\mathcal M)$
such that
$C^{\infty }(\mathcal M)$
such that
We will denote by
![]() $L^1(\mathcal M,\nu )$
the completion for
$L^1(\mathcal M,\nu )$
the completion for
![]() $\|.\|_V$
of
$\|.\|_V$
of
![]() $C^{\infty }(\mathcal M)$
.
$C^{\infty }(\mathcal M)$
.
Proof. The fact that
![]() $\nu (|f|)\geq 0$
is a consequence of
$\nu (|f|)\geq 0$
is a consequence of
![]() $\nu $
being a measure (i.e., of
$\nu $
being a measure (i.e., of
![]() $\nu $
being a distribution which is non-negative on non-negative functions). The homogeneity and the triangle inequality are clear. Suppose now
$\nu $
being a distribution which is non-negative on non-negative functions). The homogeneity and the triangle inequality are clear. Suppose now
![]() $\|f\|_V=0$
, then use equation (41) as well as equation (29) to see that the co-resonant state
$\|f\|_V=0$
, then use equation (41) as well as equation (29) to see that the co-resonant state
![]() $\nu $
gives positive measure to any non-empty open set of
$\nu $
gives positive measure to any non-empty open set of
![]() $\mathcal M$
. Thus, if f is non-zero, then
$\mathcal M$
. Thus, if f is non-zero, then
![]() $|f|$
is positive on a small open set, which is a contradiction. The change of variable formula (47) is a direct consequence of equation (45), which was shown in the proof of Theorem 3.1.
$|f|$
is positive on a small open set, which is a contradiction. The change of variable formula (47) is a direct consequence of equation (45), which was shown in the proof of Theorem 3.1.
As a direct consequence, we adapt [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Corollary 4.16] to show that there is no Ruelle resonance in the half-plane
![]() $\{\mathrm {Re}(z)> P(V+J^u)\}$
.
$\{\mathrm {Re}(z)> P(V+J^u)\}$
.
Lemma 3.4. The set of Ruelle resonances for the potential V is contained in the half-plane
![]() $\{\mathrm {Re}(\unicode{x3bb} )\leq P(V+J^u)\}$
.
$\{\mathrm {Re}(\unicode{x3bb} )\leq P(V+J^u)\}$
.
Proof. Recall from the proof of Theorem 2.1 (see [Reference Lefeuvre28, Theorem 9.11]) that we can construct an operator
![]() $ \tilde Q(\unicode{x3bb} )$
such that, as an equality on operators acting on
$ \tilde Q(\unicode{x3bb} )$
such that, as an equality on operators acting on
![]() $C^{\infty }(M)$
,
$C^{\infty }(M)$
,
where the remainder is given by
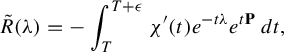 $$ \begin{align*}\tilde R(\unicode{x3bb})=-\int_T^{T+\epsilon}\chi'(t)e^{-t\unicode{x3bb}}e^{t \mathbf{P}}\,dt,\end{align*} $$
$$ \begin{align*}\tilde R(\unicode{x3bb})=-\int_T^{T+\epsilon}\chi'(t)e^{-t\unicode{x3bb}}e^{t \mathbf{P}}\,dt,\end{align*} $$
where
![]() $\chi $
is a cutoff supported in
$\chi $
is a cutoff supported in
![]() $[0,T+\epsilon [$
and constant equal to
$[0,T+\epsilon [$
and constant equal to
![]() $1$
on
$1$
on
![]() $[0,T]$
, for some suitable choices of
$[0,T]$
, for some suitable choices of
![]() $\epsilon $
and T.
$\epsilon $
and T.
Let
![]() $\unicode{x3bb} \in \mathbb C$
such that
$\unicode{x3bb} \in \mathbb C$
such that
![]() $\mathrm {Re}(\unicode{x3bb} )>P(V+J^u)$
. Let us show that it is not in the Ruelle spectrum. The projector
$\mathrm {Re}(\unicode{x3bb} )>P(V+J^u)$
. Let us show that it is not in the Ruelle spectrum. The projector
![]() $\Pi _0(\unicode{x3bb} )$
on the eigenvalue
$\Pi _0(\unicode{x3bb} )$
on the eigenvalue
![]() $z=0$
of the Fredholm operator
$z=0$
of the Fredholm operator
![]() ${F(\unicode{x3bb} ):=\mathrm {Id}-\tilde R(\unicode{x3bb} )}$
is given by the integral
${F(\unicode{x3bb} ):=\mathrm {Id}-\tilde R(\unicode{x3bb} )}$
is given by the integral
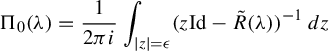 $$ \begin{align} \Pi_0(\unicode{x3bb})=\frac{1}{2\pi i}\int_{|z|=\epsilon}(z\mathrm{Id}-\tilde R(\unicode{x3bb}))^{-1}\,dz \end{align} $$
$$ \begin{align} \Pi_0(\unicode{x3bb})=\frac{1}{2\pi i}\int_{|z|=\epsilon}(z\mathrm{Id}-\tilde R(\unicode{x3bb}))^{-1}\,dz \end{align} $$
for a radius
![]() $\epsilon>0$
small enough. Note that by the proof of Theorem 2.1, this is the spectral projector for any anisotropic Sobolev space
$\epsilon>0$
small enough. Note that by the proof of Theorem 2.1, this is the spectral projector for any anisotropic Sobolev space
![]() $\mathcal H^s$
for which
$\mathcal H^s$
for which
![]() $\mathrm {Re}(\unicode{x3bb} )\geq -cs+C_0$
and thus equation (49) also holds as a map
$\mathrm {Re}(\unicode{x3bb} )\geq -cs+C_0$
and thus equation (49) also holds as a map
![]() $C^{\infty }(\mathcal M)\to \mathcal D'(\mathcal M)$
. However, if
$C^{\infty }(\mathcal M)\to \mathcal D'(\mathcal M)$
. However, if
![]() $f\in L^1(\mathcal M,\nu )$
, then, using Lemma 3.3, one has
$f\in L^1(\mathcal M,\nu )$
, then, using Lemma 3.3, one has
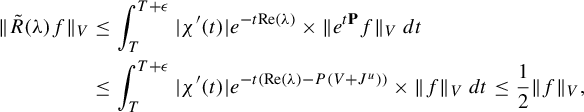 $$ \begin{align*} \|\tilde R(\unicode{x3bb})f\|_{V}&\leq \int_T^{T+\epsilon}|\chi'(t)|e^{-t\mathrm{Re}(\unicode{x3bb})}\times \|e^{t\mathbf{P}}f\|_{V}\,dt \\ & \leq \int_T^{T+\epsilon}|\chi'(t)|e^{-t(\mathrm{Re}(\unicode{x3bb})-P(V+J^u))}\times \|f\|_{V}\,dt\leq \frac 1 2\|f\|_{V}, \end{align*} $$
$$ \begin{align*} \|\tilde R(\unicode{x3bb})f\|_{V}&\leq \int_T^{T+\epsilon}|\chi'(t)|e^{-t\mathrm{Re}(\unicode{x3bb})}\times \|e^{t\mathbf{P}}f\|_{V}\,dt \\ & \leq \int_T^{T+\epsilon}|\chi'(t)|e^{-t(\mathrm{Re}(\unicode{x3bb})-P(V+J^u))}\times \|f\|_{V}\,dt\leq \frac 1 2\|f\|_{V}, \end{align*} $$
if T is chosen large enough. In particular, this shows that
![]() $F(\unicode{x3bb} )$
is invertible on
$F(\unicode{x3bb} )$
is invertible on
![]() $L^1(\mathcal M,\nu )$
with inverse in
$L^1(\mathcal M,\nu )$
with inverse in
![]() $\mathcal L(L^1(\mathcal M,\nu ))$
and thus
$\mathcal L(L^1(\mathcal M,\nu ))$
and thus
![]() $\Pi _0(\unicode{x3bb} )=0$
, meaning that
$\Pi _0(\unicode{x3bb} )=0$
, meaning that
![]() $\unicode{x3bb} $
is not a Ruelle resonance.
$\unicode{x3bb} $
is not a Ruelle resonance.
3.3 Resonances on the critical axis
In this subsection, we investigate some properties of Ruelle resonances on the critical axis and prove the first part of Theorem 1.1. The main results are that Ruelle resonances on the critical axis have no Jordan block and that the first resonance is simple.
The following two lemmas justify that resonances on the critical axis have no Jordan block. The strategy is the same as in [Reference Bonthonneau, Guillarmou, Hilgert and Weich5, Lemma 5.1], where the space
![]() $L^{\infty }$
is replaced by the new functional space
$L^{\infty }$
is replaced by the new functional space
![]() $L^1(\mathcal M,\nu )$
.
$L^1(\mathcal M,\nu )$
.
Lemma 3.5. Let
![]() $\unicode{x3bb} +P(V+J^u) \in \{\mathrm {Re}(\unicode{x3bb} )=P(V+J^u)\}$
be on the critical axis. Then,
$\unicode{x3bb} +P(V+J^u) \in \{\mathrm {Re}(\unicode{x3bb} )=P(V+J^u)\}$
be on the critical axis. Then,
![]() $\tilde R(\unicode{x3bb} )$
has spectrum included in the closed unit disk.
$\tilde R(\unicode{x3bb} )$
has spectrum included in the closed unit disk.
Proof. Consider
![]() $B\in \Psi ^0(\mathcal M)$
such that its principal symbol is equal to
$B\in \Psi ^0(\mathcal M)$
such that its principal symbol is equal to
![]() $1$
except in a conic neighborhood V of
$1$
except in a conic neighborhood V of
![]() $E_0^{*}$
. We can then write
$E_0^{*}$
. We can then write
![]() $\tilde R=\tilde RB+(\mathrm {Id}-B)\tilde R(\mathrm {Id}-B)+B\tilde R(\mathrm {Id}-B),$
where
$\tilde R=\tilde RB+(\mathrm {Id}-B)\tilde R(\mathrm {Id}-B)+B\tilde R(\mathrm {Id}-B),$
where
![]() $(\mathrm {Id}-B)\tilde R(\mathrm {Id}-B)$
is smoothing thus compact (because
$(\mathrm {Id}-B)\tilde R(\mathrm {Id}-B)$
is smoothing thus compact (because
![]() $\mathrm {WF}(\tilde R)$
does not intersect
$\mathrm {WF}(\tilde R)$
does not intersect
![]() $E_0^{*}$
, see [Reference Lefeuvre28, Theorem 9.11] for a detailed computation of the wavefront set). Moreover, we have
$E_0^{*}$
, see [Reference Lefeuvre28, Theorem 9.11] for a detailed computation of the wavefront set). Moreover, we have
![]() $\|\tilde RB+B\tilde R(\mathrm {Id}-B)\|_{L^2\to L^2}\leq \tfrac 1 2$
if T is chosen large enough. This shows that the essential spectrum of
$\|\tilde RB+B\tilde R(\mathrm {Id}-B)\|_{L^2\to L^2}\leq \tfrac 1 2$
if T is chosen large enough. This shows that the essential spectrum of
![]() $\tilde R$
is contained in
$\tilde R$
is contained in
![]() $B(0,1/2)$
and that the spectrum outside this ball consists of isolated eigenvalues. Using the
$B(0,1/2)$
and that the spectrum outside this ball consists of isolated eigenvalues. Using the
![]() $L^2\to L^2$
boundedness of
$L^2\to L^2$
boundedness of
![]() $\tilde R(\unicode{x3bb} )$
, we see that for large values of
$\tilde R(\unicode{x3bb} )$
, we see that for large values of
![]() $|z|$
, we get the converging Neumann series (in
$|z|$
, we get the converging Neumann series (in
![]() $\mathcal H^s$
)
$\mathcal H^s$
)
Now, we use the bound in equation (47) for
![]() $f\in C^{\infty }(\mathcal M)$
:
$f\in C^{\infty }(\mathcal M)$
:
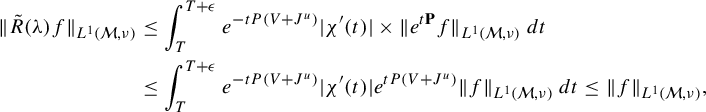 $$ \begin{align*} \|\tilde R(\unicode{x3bb})f\|_{L^{1}(\mathcal M,\nu)}&\leq \int_T^{T+\epsilon}e^{-tP(V+J^u)}|\chi'(t)|\times \|e^{t\mathbf{P}}f\|_{L^{1}(\mathcal M,\nu)}\,dt \\&\leq \int_T^{T+\epsilon}e^{-tP(V+J^u)}|\chi'(t)|e^{tP(V+J^u)}\|f\|_{L^{1}(\mathcal M,\nu)}\,dt \leq \|f\|_{L^{1}(\mathcal M,\nu)}, \end{align*} $$
$$ \begin{align*} \|\tilde R(\unicode{x3bb})f\|_{L^{1}(\mathcal M,\nu)}&\leq \int_T^{T+\epsilon}e^{-tP(V+J^u)}|\chi'(t)|\times \|e^{t\mathbf{P}}f\|_{L^{1}(\mathcal M,\nu)}\,dt \\&\leq \int_T^{T+\epsilon}e^{-tP(V+J^u)}|\chi'(t)|e^{tP(V+J^u)}\|f\|_{L^{1}(\mathcal M,\nu)}\,dt \leq \|f\|_{L^{1}(\mathcal M,\nu)}, \end{align*} $$
to get that the above Neumann series actually converges for
![]() $|z|>1$
in
$|z|>1$
in
![]() $\mathcal L(L^{1}(\mathcal M,\nu ))$
and is analytic in
$\mathcal L(L^{1}(\mathcal M,\nu ))$
and is analytic in
![]() $|z|>1$
. By density of smooth functions in
$|z|>1$
. By density of smooth functions in
![]() $\mathcal H^s $
, this proves that the eigenvalues are contained in the closed unit disk.
$\mathcal H^s $
, this proves that the eigenvalues are contained in the closed unit disk.
The next lemma, together with Remark 2.2, justifies that resonances on the critical axis have no Jordan blocks.
Lemma 3.6. A complex number
![]() $\unicode{x3bb} _0\in P(V+J^u)+i\mathbb R$
is a Ruelle resonance if and only if
$\unicode{x3bb} _0\in P(V+J^u)+i\mathbb R$
is a Ruelle resonance if and only if
![]() $\tilde R(\unicode{x3bb} _0)$
has an eigenvalue at
$\tilde R(\unicode{x3bb} _0)$
has an eigenvalue at
![]() $1$
. Moreover, if
$1$
. Moreover, if
![]() $\tilde R(\unicode{x3bb} _0)$
has a eigenvalue on the unit circle, then it is equal to
$\tilde R(\unicode{x3bb} _0)$
has a eigenvalue on the unit circle, then it is equal to
![]() $1$
and the eigenfunctions correspond to resonant states at the resonance
$1$
and the eigenfunctions correspond to resonant states at the resonance
![]() $\unicode{x3bb} _0$
. Finally, write
$\unicode{x3bb} _0$
. Finally, write
![]() $\Pi _0(\unicode{x3bb} _0)$
to be the spectral projector of
$\Pi _0(\unicode{x3bb} _0)$
to be the spectral projector of
![]() $\mathrm {Id}-\tilde R(\unicode{x3bb} _0)$
on the kernel (see equation (49)). Then, we have the convergence, in
$\mathrm {Id}-\tilde R(\unicode{x3bb} _0)$
on the kernel (see equation (49)). Then, we have the convergence, in
![]() $\mathcal L(\mathcal H^s)$
, for any
$\mathcal L(\mathcal H^s)$
, for any
![]() $s>0$
,
$s>0$
,
Proof. Suppose that
![]() $\tau \in \mathbb S^1$
is an eigenvalue of
$\tau \in \mathbb S^1$
is an eigenvalue of
![]() $\tilde R(\unicode{x3bb} _0)$
. We first check that for any smooth function u, one has
$\tilde R(\unicode{x3bb} _0)$
. We first check that for any smooth function u, one has
![]() $\mathbf {P}\tilde R(\unicode{x3bb} _0)u=\tilde R(\unicode{x3bb} _0)\mathbf {P}u.$
In other words, the operator
$\mathbf {P}\tilde R(\unicode{x3bb} _0)u=\tilde R(\unicode{x3bb} _0)\mathbf {P}u.$
In other words, the operator
![]() $\tilde R(\unicode{x3bb} _0)$
commutes with
$\tilde R(\unicode{x3bb} _0)$
commutes with
![]() $\mathbf {P}$
so that the space
$\mathbf {P}$
so that the space
![]() $\mathrm {Ran}(\Pi _{\tau }(\unicode{x3bb} _0))$
associated to the eigenvalue
$\mathrm {Ran}(\Pi _{\tau }(\unicode{x3bb} _0))$
associated to the eigenvalue
![]() $\tau \in \mathbb S^1$
can be decomposed into generalized eigenspaces of
$\tau \in \mathbb S^1$
can be decomposed into generalized eigenspaces of
![]() $\mathbf {P}$
. Suppose now that
$\mathbf {P}$
. Suppose now that
![]() $u\in \mathrm {Ran}(\Pi _{\tau }(\unicode{x3bb} _0))$
is an eigenvector for
$u\in \mathrm {Ran}(\Pi _{\tau }(\unicode{x3bb} _0))$
is an eigenvector for
![]() $\mathbf {P}$
for the eigenvalue
$\mathbf {P}$
for the eigenvalue
![]() $\mu $
, then we get
$\mu $
, then we get
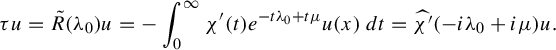 $$ \begin{align*}\tau u=\tilde R(\unicode{x3bb}_0)u=-\int_0^{\infty}\chi'(t)e^{-t\unicode{x3bb}_0+t\mu}u(x)\,dt=\widehat{\chi'}(-i\unicode{x3bb}_0+i\mu)u. \end{align*} $$
$$ \begin{align*}\tau u=\tilde R(\unicode{x3bb}_0)u=-\int_0^{\infty}\chi'(t)e^{-t\unicode{x3bb}_0+t\mu}u(x)\,dt=\widehat{\chi'}(-i\unicode{x3bb}_0+i\mu)u. \end{align*} $$
This implies that
![]() $|\widehat {\chi '}(-i\unicode{x3bb} _0+i\mu )|=1$
. However, using Lemma 3.4, we see that the real part of
$|\widehat {\chi '}(-i\unicode{x3bb} _0+i\mu )|=1$
. However, using Lemma 3.4, we see that the real part of
![]() $\mu $
is smaller than
$\mu $
is smaller than
![]() $P(V+J^u)$
, so that
$P(V+J^u)$
, so that
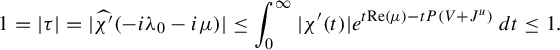 $$ \begin{align*}1=|\tau |= |\widehat{\chi'}(-i\unicode{x3bb}_0-i\mu)|\leq \int_0^{\infty}|\chi'(t)|e^{t\mathrm{Re}(\mu)-tP(V+J^u)}\,dt\leq 1.\end{align*} $$
$$ \begin{align*}1=|\tau |= |\widehat{\chi'}(-i\unicode{x3bb}_0-i\mu)|\leq \int_0^{\infty}|\chi'(t)|e^{t\mathrm{Re}(\mu)-tP(V+J^u)}\,dt\leq 1.\end{align*} $$
This implies that
![]() $\mathrm {Re}(\mu )=P(V+J^u)$
and that
$\mathrm {Re}(\mu )=P(V+J^u)$
and that
![]() $\cos (t(-i\unicode{x3bb} _0+i\mu ))$
is constant on the support of
$\cos (t(-i\unicode{x3bb} _0+i\mu ))$
is constant on the support of
![]() $\chi '$
. This is possible only if
$\chi '$
. This is possible only if
![]() $\unicode{x3bb} _0=\mu $
, which gives
$\unicode{x3bb} _0=\mu $
, which gives
![]() $\tau =1$
and shows that u is a resonant state for the Ruelle resonance
$\tau =1$
and shows that u is a resonant state for the Ruelle resonance
![]() $\unicode{x3bb} _0$
.
$\unicode{x3bb} _0$
.
The previous discussion justifies that there exists an integer N such that
We will now prove that
![]() $\tilde R(\unicode{x3bb} _0)$
has no Jordan block at
$\tilde R(\unicode{x3bb} _0)$
has no Jordan block at
![]() $1$
and deduce that
$1$
and deduce that
![]() $N=1$
. Note that the right-hand side of the previous equality does not depend on the choice of cutoff function and so that needs to be the case for the right-hand side. Let f be an eigenfunction of
$N=1$
. Note that the right-hand side of the previous equality does not depend on the choice of cutoff function and so that needs to be the case for the right-hand side. Let f be an eigenfunction of
![]() $\tilde R(\unicode{x3bb} _0)$
, then
$\tilde R(\unicode{x3bb} _0)$
, then
The above relation holds for any cutoff function
![]() $\chi $
supported in
$\chi $
supported in
![]() $[0,T+\epsilon ]$
and equal to
$[0,T+\epsilon ]$
and equal to
![]() $1$
on
$1$
on
![]() $[0,T]$
. The only condition being that T must be large enough to ensure the validity of Lemma 3.5. Approximating the Dirac mass at T (for T large enough) yields
$[0,T]$
. The only condition being that T must be large enough to ensure the validity of Lemma 3.5. Approximating the Dirac mass at T (for T large enough) yields
![]() $e^{-T\unicode{x3bb} _0+T\mathbf {P}}f=f$
and f is thus a resonant state at
$e^{-T\unicode{x3bb} _0+T\mathbf {P}}f=f$
and f is thus a resonant state at
![]() $\unicode{x3bb} _0$
. The converse is clear and we showed that the eigenfunctions of
$\unicode{x3bb} _0$
. The converse is clear and we showed that the eigenfunctions of
![]() $\tilde R(\unicode{x3bb} _0)$
at
$\tilde R(\unicode{x3bb} _0)$
at
![]() $1$
coincide with the resonant states at
$1$
coincide with the resonant states at
![]() $\unicode{x3bb} _0$
. Let
$\unicode{x3bb} _0$
. Let
![]() $u\in C^{\infty }$
, then near
$u\in C^{\infty }$
, then near
![]() $z=1$
,
$z=1$
,
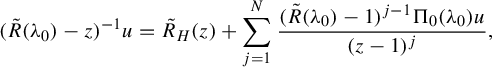 $$ \begin{align} (\tilde R(\unicode{x3bb}_0)-z)^{-1}u=\tilde R_H(z)+\sum_{j=1}^{N}\frac{(\tilde R(\unicode{x3bb}_0) -1)^{j-1}\Pi_0(\unicode{x3bb}_0)u}{(z-1)^j}, \end{align} $$
$$ \begin{align} (\tilde R(\unicode{x3bb}_0)-z)^{-1}u=\tilde R_H(z)+\sum_{j=1}^{N}\frac{(\tilde R(\unicode{x3bb}_0) -1)^{j-1}\Pi_0(\unicode{x3bb}_0)u}{(z-1)^j}, \end{align} $$
where
![]() $R_+^H(z)$
is the holomorphic part near
$R_+^H(z)$
is the holomorphic part near
![]() $z=1$
. We note that
$z=1$
. We note that
![]() $(\tilde R(\unicode{x3bb} _0) -1)^{N-1}\Pi _0(\unicode{x3bb} _0)u$
is an eigenevector of
$(\tilde R(\unicode{x3bb} _0) -1)^{N-1}\Pi _0(\unicode{x3bb} _0)u$
is an eigenevector of
![]() $\tilde R(\unicode{x3bb} )$
for
$\tilde R(\unicode{x3bb} )$
for
![]() $1$
. By the previous discussion, it is thus a resonant state
$1$
. By the previous discussion, it is thus a resonant state
![]() $\theta $
associated to
$\theta $
associated to
![]() $\unicode{x3bb} _0$
. By Lemma 3.1, we can consider a co-resonant state
$\unicode{x3bb} _0$
. By Lemma 3.1, we can consider a co-resonant state
![]() $\mu $
such that the pairing
$\mu $
such that the pairing
![]() $(\theta , \mu )\neq 0$
. On one hand, using equation (52) gives, near
$(\theta , \mu )\neq 0$
. On one hand, using equation (52) gives, near
![]() $z=1$
,
$z=1$
,
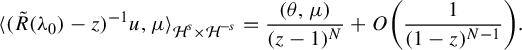 $$ \begin{align} \langle (\tilde R(\unicode{x3bb}_0)-z)^{-1}u,\mu\rangle_{\mathcal H^s\times \mathcal H^{-s}}=\frac{(\theta, \mu)}{(z-1)^{N}}+O\bigg(\frac{1}{(1-z)^{N-1}}\bigg). \end{align} $$
$$ \begin{align} \langle (\tilde R(\unicode{x3bb}_0)-z)^{-1}u,\mu\rangle_{\mathcal H^s\times \mathcal H^{-s}}=\frac{(\theta, \mu)}{(z-1)^{N}}+O\bigg(\frac{1}{(1-z)^{N-1}}\bigg). \end{align} $$
However, on the other hand, for any
![]() $|z|>1$
, one has, for any
$|z|>1$
, one has, for any
![]() $k\geq 0$
,
$k\geq 0$
,
Summing the Neumann series then gives
Going back to equation (41), this is possible only if
![]() $N=1$
. In particular, resonances on the critical axis have no Jordan block. Finally, we use that
$N=1$
. In particular, resonances on the critical axis have no Jordan block. Finally, we use that
where the spectral radius of
![]() $K(\unicode{x3bb} _0)$
on
$K(\unicode{x3bb} _0)$
on
![]() $\mathcal H^s$
is strictly smaller than
$\mathcal H^s$
is strictly smaller than
![]() $1$
. Remember that if
$1$
. Remember that if
![]() $r<1$
is the spectral radius of
$r<1$
is the spectral radius of
![]() $K(\unicode{x3bb} _0)$
, then for any
$K(\unicode{x3bb} _0)$
, then for any
![]() $\epsilon>0$
small enough, one has
$\epsilon>0$
small enough, one has
Thus, as bounded operators on
![]() $\mathcal H^s$
, we get, as
$\mathcal H^s$
, we get, as
![]() $n\to +\infty $
,
$n\to +\infty $
,
![]() $ \tilde R(\unicode{x3bb} _0)^n=\Pi _0(\unicode{x3bb} _0)+K(\unicode{x3bb} _0)^n\to \Pi _0(\unicode{x3bb} _0).$
$ \tilde R(\unicode{x3bb} _0)^n=\Pi _0(\unicode{x3bb} _0)+K(\unicode{x3bb} _0)^n\to \Pi _0(\unicode{x3bb} _0).$
We now identify the co-resonant states associated to resonances on the critical axis to equivariant measures with wavefront set contained in
![]() $E_s^{*}$
, and show that the space of (co)-resonant states at the first resonance is one-dimensional and spanned by the measure constructed in Theorem 3.1. First, define for
$E_s^{*}$
, and show that the space of (co)-resonant states at the first resonance is one-dimensional and spanned by the measure constructed in Theorem 3.1. First, define for
![]() $v\in C^{\infty }(\mathcal M,[0,+\infty [)$
a (complex) Radon measure
$v\in C^{\infty }(\mathcal M,[0,+\infty [)$
a (complex) Radon measure
![]() $\mu _v^{\unicode{x3bb} }$
such that
$\mu _v^{\unicode{x3bb} }$
such that
Proposition 3.1. (Resonant states on the critical axis)
Let
![]() $\unicode{x3bb} \in P(V+J^u)+i\mathbb R$
be a Ruelle resonance on the critical axis. The space of co-resonant states at
$\unicode{x3bb} \in P(V+J^u)+i\mathbb R$
be a Ruelle resonance on the critical axis. The space of co-resonant states at
![]() $\unicode{x3bb} $
is equal to
$\unicode{x3bb} $
is equal to
![]() $\Pi _0^{*}(\unicode{x3bb} )(C^{\infty }(\mathcal M))=\Pi _0^{*}(\unicode{x3bb} )(\mathcal H^{-s})$
. More precisely, we have the following isomorphism:
$\Pi _0^{*}(\unicode{x3bb} )(C^{\infty }(\mathcal M))=\Pi _0^{*}(\unicode{x3bb} )(\mathcal H^{-s})$
. More precisely, we have the following isomorphism:
Finally, all these measures are absolutely continuous with respect to the measure
![]() $\mu _1^{P(V+J^u)}$
with bounded densities.
$\mu _1^{P(V+J^u)}$
with bounded densities.
Proof. Let
![]() $v\in C^{\infty }(\mathcal M,[0,+\infty [)$
and first consider
$v\in C^{\infty }(\mathcal M,[0,+\infty [)$
and first consider
![]() $\unicode{x3bb} =P(V+J^u)$
. Then, using Lemma 3.6, we get
$\unicode{x3bb} =P(V+J^u)$
. Then, using Lemma 3.6, we get
![]() $\tilde R(\unicode{x3bb} )^n\to \Pi _0(\unicode{x3bb} )$
in
$\tilde R(\unicode{x3bb} )^n\to \Pi _0(\unicode{x3bb} )$
in
![]() $\mathcal L(\mathcal H^s)$
. Now, for any
$\mathcal L(\mathcal H^s)$
. Now, for any
![]() $u\in C^{\infty }(\mathcal M,[0,+\infty [)$
,
$u\in C^{\infty }(\mathcal M,[0,+\infty [)$
,
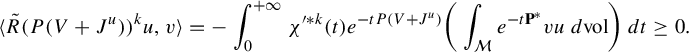 $$ \begin{align*} \langle \tilde R(P(V+J^u))^ku,v\rangle &= -\int_{0}^{+\infty}\chi^{\prime *k}(t)e^{-tP(V+J^u)}\bigg(\int_{\mathcal M}e^{-t\mathbf{P}^{*}}vu\,d\mathrm{vol} \bigg)\,dt\geq 0. \end{align*} $$
$$ \begin{align*} \langle \tilde R(P(V+J^u))^ku,v\rangle &= -\int_{0}^{+\infty}\chi^{\prime *k}(t)e^{-tP(V+J^u)}\bigg(\int_{\mathcal M}e^{-t\mathbf{P}^{*}}vu\,d\mathrm{vol} \bigg)\,dt\geq 0. \end{align*} $$
This proves that
![]() $\langle \Pi _0(P(V+J^u))u,v\rangle \geq 0$
, which gives that
$\langle \Pi _0(P(V+J^u))u,v\rangle \geq 0$
, which gives that
![]() $\mu _v$
is a non-negative Radon measure for
$\mu _v$
is a non-negative Radon measure for
![]() $v\geq 0$
. Consider a general resonance on the critical axis
$v\geq 0$
. Consider a general resonance on the critical axis
![]() $\unicode{x3bb} =ib+P(V+J^u)$
with
$\unicode{x3bb} =ib+P(V+J^u)$
with
![]() $b\in \mathbb R$
and
$b\in \mathbb R$
and
![]() $v\leq v'\in C^{\infty }(\mathcal M, [0,+\infty [)$
, we get
$v\leq v'\in C^{\infty }(\mathcal M, [0,+\infty [)$
, we get
Passing to the limit, we get first that
![]() $\mu _v^{\unicode{x3bb} }$
defines an order
$\mu _v^{\unicode{x3bb} }$
defines an order
![]() $0$
distribution and thus defines a (complex) measure. Moreover, the last inequality actually proves that
$0$
distribution and thus defines a (complex) measure. Moreover, the last inequality actually proves that
![]() $\mu _v^{\unicode{x3bb} }\ll \mu _{v'}$
with a density bounded by
$\mu _v^{\unicode{x3bb} }\ll \mu _{v'}$
with a density bounded by
![]() $1$
. In particular, one gets that every measure
$1$
. In particular, one gets that every measure
![]() $ \mu _v^{\unicode{x3bb} }$
is absolutely continuous with respect to the measure
$ \mu _v^{\unicode{x3bb} }$
is absolutely continuous with respect to the measure
![]() $\mu _1$
.
$\mu _1$
.
We can now prove the first part of Theorem 1.1 for the action on
![]() $0$
-forms.
$0$
-forms.
Proposition 3.2. Under Assumption 1, the first Ruelle resonance
![]() $P(V+J^u)$
for the action on
$P(V+J^u)$
for the action on
![]() $0$
-forms is simple with a space of co-resonant state spanned by
$0$
-forms is simple with a space of co-resonant state spanned by
![]() $\nu $
.
$\nu $
.
Proof. Consider a co-resonant state
![]() $\mu $
for the first Ruelle resonance
$\mu $
for the first Ruelle resonance
![]() $P(V+J^u)$
. We know by the previous proposition that
$P(V+J^u)$
. We know by the previous proposition that
![]() $\mu $
is a measure with wavefront set contained in
$\mu $
is a measure with wavefront set contained in
![]() $E_s^{*}$
and we will suppose that it is a non-negative measure. The wavefront set condition, together with [Reference Hormander26, Corollary 8.2.7], justifies that one can restrict the distribution
$E_s^{*}$
and we will suppose that it is a non-negative measure. The wavefront set condition, together with [Reference Hormander26, Corollary 8.2.7], justifies that one can restrict the distribution
![]() $\mu $
to any unstable manifold
$\mu $
to any unstable manifold
![]() $\mathcal W^u(x)$
. We will denote by
$\mathcal W^u(x)$
. We will denote by
![]() $\mu _x:=\mu _{|\mathcal W^u(x)}$
. More explicitly, for a smooth function
$\mu _x:=\mu _{|\mathcal W^u(x)}$
. More explicitly, for a smooth function
![]() $f\in C^{\infty }(\mathcal M)$
, we can define, for some
$f\in C^{\infty }(\mathcal M)$
, we can define, for some
![]() $s\in \mathbb R$
,
$s\in \mathbb R$
,
where the bracket denotes the distributional pairing and
![]() $\delta _{\mathcal W^u(x)}$
denotes the integration over the unstable manifold
$\delta _{\mathcal W^u(x)}$
denotes the integration over the unstable manifold
![]() $\mathcal W^u(x)$
defined by
$\mathcal W^u(x)$
defined by
 $$ \begin{align} (f, \delta_{\mathcal W^u(x)}):=\int_{\mathcal W^u(x)}f(y)\,d\mathrm{vol}_{\mathcal W^u(x)}(y). \end{align} $$
$$ \begin{align} (f, \delta_{\mathcal W^u(x)}):=\int_{\mathcal W^u(x)}f(y)\,d\mathrm{vol}_{\mathcal W^u(x)}(y). \end{align} $$
The fact that the distributional pairing coincides with the
![]() $\mathcal H^s \times \mathcal H^{-s}$
pairing is a consequence of the wavefront set condition on the distributions. In particular,
$\mathcal H^s \times \mathcal H^{-s}$
pairing is a consequence of the wavefront set condition on the distributions. In particular,
![]() $\mu _x$
is a non-negative distribution as the product of two non-negative distributions. The restrictions
$\mu _x$
is a non-negative distribution as the product of two non-negative distributions. The restrictions
![]() $\{\mu _x \mid x\in \mathcal M\}$
define a system of
$\{\mu _x \mid x\in \mathcal M\}$
define a system of
![]() $\mathcal W^{ws}$
-transversal measures in the sense of [Reference Climenhaga10]. The strategy to show that the first resonance is simple is to use [Reference Climenhaga10, Corollary 3.12], which asserts that the only system (up to constant rescaling) of
$\mathcal W^{ws}$
-transversal measures in the sense of [Reference Climenhaga10]. The strategy to show that the first resonance is simple is to use [Reference Climenhaga10, Corollary 3.12], which asserts that the only system (up to constant rescaling) of
![]() $\mathcal W^{ws}$
-transversal measures which satisfies
$\mathcal W^{ws}$
-transversal measures which satisfies
![]() $\varphi _t$
-conformality (see equation (30)) and the change of variable by holonomy (see equation (35)) is
$\varphi _t$
-conformality (see equation (30)) and the change of variable by holonomy (see equation (35)) is
![]() $m^u_{V+J^u}$
.
$m^u_{V+J^u}$
.
The system of measures
![]() $\{\mu _x \mid x\in \mathcal M\}$
satisfies
$\{\mu _x \mid x\in \mathcal M\}$
satisfies
![]() $\varphi _t$
-conformality. This is a consequence of the fact that
$\varphi _t$
-conformality. This is a consequence of the fact that
![]() $\mu $
is a co-resonant state. More precisely, for any smooth function
$\mu $
is a co-resonant state. More precisely, for any smooth function
![]() ${f\in C^{\infty }(\mathcal M)}$
, we can write
${f\in C^{\infty }(\mathcal M)}$
, we can write
Using
![]() $e^{t\mathbf P}( f\delta _{\mathcal W^u(x)})=e^{t\mathbf P} fe^{-tX}\delta _{\mathcal W^u(x)}$
, then yields
$e^{t\mathbf P}( f\delta _{\mathcal W^u(x)})=e^{t\mathbf P} fe^{-tX}\delta _{\mathcal W^u(x)}$
, then yields
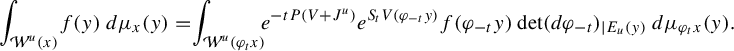 $$ \begin{align*} \int_{\mathcal W^u(x)}\! f(y)\,d\mu_x(y)=\!\int_{\mathcal W^u(\varphi_t x)}\!\!e^{-tP(V+J^u)}e^{S_tV(\varphi_{-t}y)}f(\varphi_{-t}y) \det (d\varphi_{-t})_{|E_u(y)}\,d\mu_{\varphi_t x}(y).\end{align*} $$
$$ \begin{align*} \int_{\mathcal W^u(x)}\! f(y)\,d\mu_x(y)=\!\int_{\mathcal W^u(\varphi_t x)}\!\!e^{-tP(V+J^u)}e^{S_tV(\varphi_{-t}y)}f(\varphi_{-t}y) \det (d\varphi_{-t})_{|E_u(y)}\,d\mu_{\varphi_t x}(y).\end{align*} $$
This rewrites
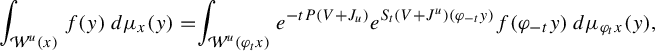 $$ \begin{align*}\int_{\mathcal W^u(x)}f(y)\,d\mu_x(y)=\! \int_{\mathcal W^u(\varphi_t x)}e^{-tP(V+J_u)}e^{S_t(V+J^u)(\varphi_{-t}y)}f(\varphi_{-t}y)\,d\mu_{\varphi_t x}(y),\end{align*} $$
$$ \begin{align*}\int_{\mathcal W^u(x)}f(y)\,d\mu_x(y)=\! \int_{\mathcal W^u(\varphi_t x)}e^{-tP(V+J_u)}e^{S_t(V+J^u)(\varphi_{-t}y)}f(\varphi_{-t}y)\,d\mu_{\varphi_t x}(y),\end{align*} $$
which is exactly
![]() $\varphi _t$
-conformality for the potential
$\varphi _t$
-conformality for the potential
![]() $V+J^u$
.
$V+J^u$
.
The system of measures
![]() $\{\mu _x \mid x\in \mathcal M\}$
satisfies the change of variable by holonomy. Investigating the proof of [Reference Climenhaga10, Corollary 3.12], we see that we only need to show the change of variable formula for the standard
$\{\mu _x \mid x\in \mathcal M\}$
satisfies the change of variable by holonomy. Investigating the proof of [Reference Climenhaga10, Corollary 3.12], we see that we only need to show the change of variable formula for the standard
![]() $\delta _0$
-holonomy given by
$\delta _0$
-holonomy given by
![]() $\mathcal W^u(x)\ni z\mapsto \pi (z):=[z,x']\in \mathcal W^u(x')$
. We have the following facts.
$\mathcal W^u(x)\ni z\mapsto \pi (z):=[z,x']\in \mathcal W^u(x')$
. We have the following facts.
-
• For all
 $x,x'\kern1.3pt{\in}\kern1.3pt \mathcal M$
,
$x,x'\kern1.3pt{\in}\kern1.3pt \mathcal M$
,
 $x\kern1.3pt{\neq}\kern1.3pt x'$
close, one has
$x\kern1.3pt{\neq}\kern1.3pt x'$
close, one has
 $L_{x,x'}:\phi \kern1.3pt{\in}\kern1.3pt C^{0}(\mathcal M)\kern1.3pt{\mapsto}\kern1.3pt {(\mu _x\kern1.3pt{-}\kern1.3pt\mu _{x'},\phi )}/{d(x,x')^{\alpha }}$
is linear.
$L_{x,x'}:\phi \kern1.3pt{\in}\kern1.3pt C^{0}(\mathcal M)\kern1.3pt{\mapsto}\kern1.3pt {(\mu _x\kern1.3pt{-}\kern1.3pt\mu _{x'},\phi )}/{d(x,x')^{\alpha }}$
is linear. -
• For any
 $\phi \in C^{0}(\mathcal M)$
, one has
$\phi \in C^{0}(\mathcal M)$
, one has
 $\sup _{x\neq x'} |L_{x,x'}(\phi )|<+\infty $
by equation (A.1).
$\sup _{x\neq x'} |L_{x,x'}(\phi )|<+\infty $
by equation (A.1). -
• The space
 $C^{0}(\mathcal M)$
is a Banach space.
$C^{0}(\mathcal M)$
is a Banach space.
We can apply the Banach–Steinhauss theorem to get
![]() $\sup _{x\neq x'} \|L_{x,x'}\|_{\mathrm {op}}=C<+\infty $
, i.e.,
$\sup _{x\neq x'} \|L_{x,x'}\|_{\mathrm {op}}=C<+\infty $
, i.e.,
Now consider
![]() $\mathcal W^u(x)\ni z\mapsto \pi (z):=[z,x']\in \mathcal W^u(x')$
. Our goal is to relate
$\mathcal W^u(x)\ni z\mapsto \pi (z):=[z,x']\in \mathcal W^u(x')$
. Our goal is to relate
![]() $\mu _x$
and
$\mu _x$
and
![]() $\pi _{x'}^{*}\mu _{x'}$
. Consider
$\pi _{x'}^{*}\mu _{x'}$
. Consider
![]() $f\in C^0(\mathcal W^u(x,\delta _0))$
. Since the foliation is Hölder, we can extend f locally on a small rectangle by making it constant on weak-stable manifolds, and this defines a continuous function
$f\in C^0(\mathcal W^u(x,\delta _0))$
. Since the foliation is Hölder, we can extend f locally on a small rectangle by making it constant on weak-stable manifolds, and this defines a continuous function
![]() $\bar f$
. We are now left with relating
$\bar f$
. We are now left with relating
![]() $\mu _x(\bar f)$
and
$\mu _x(\bar f)$
and
![]() $\mu _{x'}(\bar f)$
.
$\mu _{x'}(\bar f)$
.
First, consider the Bowen time
![]() $t=t(x,x')$
such that
$t=t(x,x')$
such that
![]() $\varphi _tx\in \mathcal W^s(x')$
. Then,
$\varphi _tx\in \mathcal W^s(x')$
. Then,
![]() $\varphi _t$
- conformality shows that
$\varphi _t$
- conformality shows that
![]() ${d[(\varphi _t)_*\mu _x]}/{d\mu _{\varphi _tx}}(z)=e^{S_t(V+J^u)(z)-tP(V+J^u)}$
. Now, for any
${d[(\varphi _t)_*\mu _x]}/{d\mu _{\varphi _tx}}(z)=e^{S_t(V+J^u)(z)-tP(V+J^u)}$
. Now, for any
![]() $\tau>0$
, we can use
$\tau>0$
, we can use
![]() $\varphi _t$
-conformality again to get
$\varphi _t$
-conformality again to get
![]() ${d[(\varphi _\tau )_*\mu _{\varphi _tx}]}/{d \mu _{\varphi _{t+\tau }x}}(z)=e^{S_{\tau }(V+J^u)(z)-\tau P(V+J^u)}$
and
${d[(\varphi _\tau )_*\mu _{\varphi _tx}]}/{d \mu _{\varphi _{t+\tau }x}}(z)=e^{S_{\tau }(V+J^u)(z)-\tau P(V+J^u)}$
and
![]() ${d[(\varphi _\tau )_*\mu _{x'}]}/{d\mu _{\varphi _\tau x'}}(y)=e^{S_{\tau }(V+J^u)(y)-\tau P(V+J^u)} $
. Now, we have that
${d[(\varphi _\tau )_*\mu _{x'}]}/{d\mu _{\varphi _\tau x'}}(y)=e^{S_{\tau }(V+J^u)(y)-\tau P(V+J^u)} $
. Now, we have that
![]() $d(\varphi _{t+\tau }x, \varphi _\tau x')\leq Ce^{-\eta \tau }$
and the above continuity then shows that
$d(\varphi _{t+\tau }x, \varphi _\tau x')\leq Ce^{-\eta \tau }$
and the above continuity then shows that
![]() $|\mu _{\varphi _{t+\tau }x}( \bar f)-\mu _{\varphi _\tau x'}(\bar f)|\to 0$
when
$|\mu _{\varphi _{t+\tau }x}( \bar f)-\mu _{\varphi _\tau x'}(\bar f)|\to 0$
when
![]() $\tau \to +\infty $
. This means that the overall holonomy factor is given by the following limit:
$\tau \to +\infty $
. This means that the overall holonomy factor is given by the following limit:
which is exactly equal to
![]() $e^{w_{V+J^u}^+(z,y)}$
, see the proof of [Reference Climenhaga10, Theorem 3.9] for a more detailed argument.
$e^{w_{V+J^u}^+(z,y)}$
, see the proof of [Reference Climenhaga10, Theorem 3.9] for a more detailed argument.
The first resonance
![]() $P(V+J^u)$
is simple. We can use [Reference Climenhaga10, Corollary 3.12] to claim that there is a constant
$P(V+J^u)$
is simple. We can use [Reference Climenhaga10, Corollary 3.12] to claim that there is a constant
![]() $c>0$
such that for any
$c>0$
such that for any
![]() $x\in \mathcal M$
, one has
$x\in \mathcal M$
, one has
![]() $\mu _x=c m^u_{x,V+J^u}$
. We now would like to deduce that this implies
$\mu _x=c m^u_{x,V+J^u}$
. We now would like to deduce that this implies
![]() $\mu =c\nu $
by proving a Fubini-like formula for distributions with wavefront set in
$\mu =c\nu $
by proving a Fubini-like formula for distributions with wavefront set in
![]() $E_s^{*}$
. For this, we first need to disintegrate the volume measure with respect to the unstable foliation and an arbitrary (smooth) transversal complementary foliation G. More precisely, we will use [Reference Bonthonneau, Guillarmou and Weich4, Proposition 1.6], which states that in a product neighborhood U around a point
$E_s^{*}$
. For this, we first need to disintegrate the volume measure with respect to the unstable foliation and an arbitrary (smooth) transversal complementary foliation G. More precisely, we will use [Reference Bonthonneau, Guillarmou and Weich4, Proposition 1.6], which states that in a product neighborhood U around a point
![]() $q\in \mathcal M$
, there is a continuous function
$q\in \mathcal M$
, there is a continuous function
![]() $\delta _u: U\to \mathbb R_+$
such that
$\delta _u: U\to \mathbb R_+$
such that
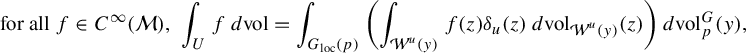 $$ \begin{align*} \text{for all } f\in C^{\infty}(\mathcal M),\ \int_U f\,d\mathrm{vol}=\int_{G_{\mathrm{loc}}(p)}\bigg(\!\int_{\mathcal W^u(y)}f(z)\delta_u(z)\,d\mathrm{vol}_{\mathcal W^u(y)}(z)\bigg)\,d\mathrm{vol}_p^G(y), \end{align*} $$
$$ \begin{align*} \text{for all } f\in C^{\infty}(\mathcal M),\ \int_U f\,d\mathrm{vol}=\int_{G_{\mathrm{loc}}(p)}\bigg(\!\int_{\mathcal W^u(y)}f(z)\delta_u(z)\,d\mathrm{vol}_{\mathcal W^u(y)}(z)\bigg)\,d\mathrm{vol}_p^G(y), \end{align*} $$
where
![]() $G_{\mathrm {loc}}(p)$
is the connected component of the element of the partition of G containing p. Actually, the conditional density
$G_{\mathrm {loc}}(p)$
is the connected component of the element of the partition of G containing p. Actually, the conditional density
![]() $\delta _u$
is smooth along the leaves in the following sense:
$\delta _u$
is smooth along the leaves in the following sense:
is finite for any k and that the norm depends continuously in x. This regularity condition allows to integrate by parts in the inner integral and, in particular, an immediate adaptation of [Reference Bonthonneau, Guillarmou and Weich4, Lemma 1.9] yields
![]() $\mathrm {WF}(\delta _u(z) \delta _{\mathcal W^u(y)})\subset E_u^{*}\oplus E_0^{*}$
. Here, we have denoted by
$\mathrm {WF}(\delta _u(z) \delta _{\mathcal W^u(y)})\subset E_u^{*}\oplus E_0^{*}$
. Here, we have denoted by
![]() $\delta _u(z) \delta _{\mathcal W^u(y)}$
the distribution:
$\delta _u(z) \delta _{\mathcal W^u(y)}$
the distribution:
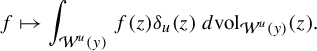 $$ \begin{align*}f\mapsto \int_{\mathcal W^u(y)}f(z)\delta_u(z)\,d\mathrm{vol}_{\mathcal W^u(y)}(z).\end{align*} $$
$$ \begin{align*}f\mapsto \int_{\mathcal W^u(y)}f(z)\delta_u(z)\,d\mathrm{vol}_{\mathcal W^u(y)}(z).\end{align*} $$
In particular, we consider
![]() $f_n\in C^{\infty }(\mathcal M)$
such that
$f_n\in C^{\infty }(\mathcal M)$
such that
![]() $f_n\to \mu $
is
$f_n\to \mu $
is
![]() $\mathcal D^{\prime }_{\Gamma }(\mathcal M)$
, where
$\mathcal D^{\prime }_{\Gamma }(\mathcal M)$
, where
![]() $\Gamma $
is a conic neighborhood of
$\Gamma $
is a conic neighborhood of
![]() $E_s^{*}$
which does not intersect
$E_s^{*}$
which does not intersect
![]() $E_u^{*}\oplus E_0^{*}$
, and we can use the continuity of the distributional product (see [Reference Lefeuvre28, Lemma 4.2.7]) to write for any
$E_u^{*}\oplus E_0^{*}$
, and we can use the continuity of the distributional product (see [Reference Lefeuvre28, Lemma 4.2.7]) to write for any
![]() $f\in C^{\infty }(\mathcal M)$
,
$f\in C^{\infty }(\mathcal M)$
,
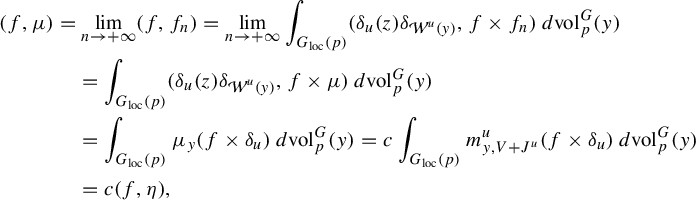 $$ \begin{align*}(f,\mu)=&\lim_{n\to +\infty}(f,f_n)= \lim_{n\to +\infty}\int_{G_{\mathrm{loc}}(p)} (\delta_u(z) \delta_{\mathcal W^u(y)},f\times f_n)\,d\mathrm{vol}_p^G(y) \\&=\int_{G_{\mathrm{loc}}(p)} (\delta_u(z) \delta_{\mathcal W^u(y)},f\times \mu)\,d\mathrm{vol}_p^G(y) \\&= \int_{G_{\mathrm{loc}}(p)} \mu_y(f\times \delta_u)\,d\mathrm{vol}_p^G(y)=c\int_{G_{\mathrm{loc}}(p)} m^u_{y,V+J^u}(f\times \delta_u)\,d\mathrm{vol}_p^G(y) \\&=c(f,\eta), \end{align*} $$
$$ \begin{align*}(f,\mu)=&\lim_{n\to +\infty}(f,f_n)= \lim_{n\to +\infty}\int_{G_{\mathrm{loc}}(p)} (\delta_u(z) \delta_{\mathcal W^u(y)},f\times f_n)\,d\mathrm{vol}_p^G(y) \\&=\int_{G_{\mathrm{loc}}(p)} (\delta_u(z) \delta_{\mathcal W^u(y)},f\times \mu)\,d\mathrm{vol}_p^G(y) \\&= \int_{G_{\mathrm{loc}}(p)} \mu_y(f\times \delta_u)\,d\mathrm{vol}_p^G(y)=c\int_{G_{\mathrm{loc}}(p)} m^u_{y,V+J^u}(f\times \delta_u)\,d\mathrm{vol}_p^G(y) \\&=c(f,\eta), \end{align*} $$
where we used the continuity of the density and the fact that
![]() $\mu _x$
is of order
$\mu _x$
is of order
![]() $0$
. Together with the previous lemma, this proves that all co-resonant states are proportional, and thus that
$0$
. Together with the previous lemma, this proves that all co-resonant states are proportional, and thus that
![]() $P(V+J^u)$
is simple and concludes the proof.
$P(V+J^u)$
is simple and concludes the proof.
We can now prove Theorem 1.2 for the action on
![]() $0$
-forms.
$0$
-forms.
Proposition 3.3. The equilibrium state (see equation (17))
![]() $\mu _{V+J^u}$
is equal to
$\mu _{V+J^u}$
is equal to
![]() $=c\eta \times \nu $
or is given by the averaging formula (8). Finally, if the flow is weak mixing with respect to the equilibrium state
$=c\eta \times \nu $
or is given by the averaging formula (8). Finally, if the flow is weak mixing with respect to the equilibrium state
![]() $\mu _{V+J^u}$
, then the only resonance on the critical axis is
$\mu _{V+J^u}$
, then the only resonance on the critical axis is
![]() $P(V+J^u)$
.
$P(V+J^u)$
.
Proof.
The co-resonant state
![]() $\nu $
is absolutely continuous with respect to
$\nu $
is absolutely continuous with respect to
![]() $\mu _{V+J^u}$
. We follow the proof of [Reference Climenhaga10, Theorem 3.10] and prove that there exists a constant
$\mu _{V+J^u}$
. We follow the proof of [Reference Climenhaga10, Theorem 3.10] and prove that there exists a constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $q\in \mathcal M$
and
$q\in \mathcal M$
and
![]() $t\geq 0$
such that
$t\geq 0$
such that
which suffices as
![]() $\mu _{V+J^u}$
is the the Gibbs state (see [Reference Fisher and Hasselblatt19, Theorem 4.3.26]). From the proof of [Reference Climenhaga10, Theorem 3.10], we get that
$\mu _{V+J^u}$
is the the Gibbs state (see [Reference Fisher and Hasselblatt19, Theorem 4.3.26]). From the proof of [Reference Climenhaga10, Theorem 3.10], we get that
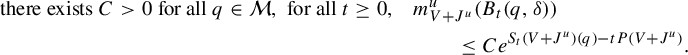 $$ \begin{align*} \text{there exists } C>0 \text{ for all } q\in \mathcal M, \text{ for all } t\geq 0, \quad &m^{u}_{V+J^{u}}(B_t(q,\delta))\\ &\qquad\leq C e^{S_t(V+J^u)(q)-tP(V+J^u)}. \end{align*} $$
$$ \begin{align*} \text{there exists } C>0 \text{ for all } q\in \mathcal M, \text{ for all } t\geq 0, \quad &m^{u}_{V+J^{u}}(B_t(q,\delta))\\ &\qquad\leq C e^{S_t(V+J^u)(q)-tP(V+J^u)}. \end{align*} $$
Now, we can use equation (43), the fact that the integrand
![]() $e^{w_{J^u}^-(z,x)}$
is uniformly bounded on
$e^{w_{J^u}^-(z,x)}$
is uniformly bounded on
![]() $\mathcal M$
, and
$\mathcal M$
, and
![]() $m^{ws}_{q,J^u}(R_q^{ws})$
is uniformly bounded in q (see [Reference Climenhaga10, Theorem 3.1]) to get equation (57).
$m^{ws}_{q,J^u}(R_q^{ws})$
is uniformly bounded in q (see [Reference Climenhaga10, Theorem 3.1]) to get equation (57).
Product formula and averaging formula. Let
![]() $\eta $
be the resonant state, which we can obtain by applying Theorem 3.1 to the dual
$\eta $
be the resonant state, which we can obtain by applying Theorem 3.1 to the dual
![]() $\mathbf {P}^{*}$
. We have
$\mathbf {P}^{*}$
. We have
![]() $\mathrm {WF}(\eta ) \subset E_u^{*}$
,
$\mathrm {WF}(\eta ) \subset E_u^{*}$
,
![]() $\mathrm {WF}(\nu ) \subset E_s^{*}$
and we have
$\mathrm {WF}(\nu ) \subset E_s^{*}$
and we have
![]() $E_s^{*}\cap E_u^{*} \cap (T^{*}\mathcal M\setminus \{0\}) = \emptyset $
, which shows that the distributional product of
$E_s^{*}\cap E_u^{*} \cap (T^{*}\mathcal M\setminus \{0\}) = \emptyset $
, which shows that the distributional product of
![]() $\eta $
and
$\eta $
and
![]() $\nu $
is well defined. Actually, we can use the duality in equation (21) to define the product:
$\nu $
is well defined. Actually, we can use the duality in equation (21) to define the product:
where the equality is justified by equation (22). From the fact that
![]() $\nu $
and
$\nu $
and
![]() $\eta $
are non-negative measures (see Proposition 3.1), and equation (58), we see that this is also the case of their product
$\eta $
are non-negative measures (see Proposition 3.1), and equation (58), we see that this is also the case of their product
![]() $\eta \times \nu $
. It is easily seen to be invariant by the flow:
$\eta \times \nu $
. It is easily seen to be invariant by the flow:
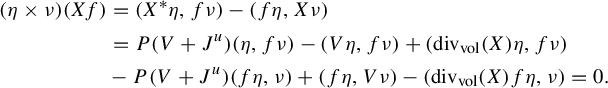 $$ \begin{align*} (\eta \times \nu)(Xf)&=( X^{*}\eta,f\nu)-(f\eta,X\nu) \\&=P(V+J^u)(\eta,f\nu)-(V\eta,f\nu)+(\mathrm{div}_{\mathrm{vol}}(X)\eta,f\nu) \\&-P(V+J^u)(f\eta,\nu)+(f\eta,V\nu)-(\mathrm{div}_{\mathrm{vol}}(X)f \eta,\nu)=0. \end{align*} $$
$$ \begin{align*} (\eta \times \nu)(Xf)&=( X^{*}\eta,f\nu)-(f\eta,X\nu) \\&=P(V+J^u)(\eta,f\nu)-(V\eta,f\nu)+(\mathrm{div}_{\mathrm{vol}}(X)\eta,f\nu) \\&-P(V+J^u)(f\eta,\nu)+(f\eta,V\nu)-(\mathrm{div}_{\mathrm{vol}}(X)f \eta,\nu)=0. \end{align*} $$
We prove that the product is absolutely continuous with respect to
![]() $\mu _{V+J^u}$
. For this, we use Proposition 3.1 and the previous proposition to get
$\mu _{V+J^u}$
. For this, we use Proposition 3.1 and the previous proposition to get
![]() $\Pi _0(P(V+J^u))1=c\eta $
for some
$\Pi _0(P(V+J^u))1=c\eta $
for some
![]() $c>0$
. Now, this means that we can compute
$c>0$
. Now, this means that we can compute
![]() $(\eta \times \nu )(f)$
for
$(\eta \times \nu )(f)$
for
![]() $f\in C^{\infty }(\mathcal M)$
:
$f\in C^{\infty }(\mathcal M)$
:
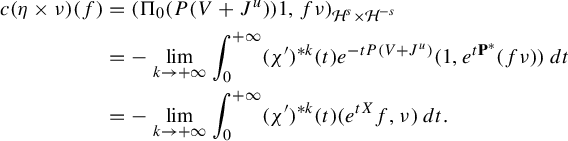 $$ \begin{align*} c(\eta \times \nu)(f)&=( \Pi_0(P(V+J^u))1,f\nu)_{\mathcal H^s \times \mathcal H^{-s}} \\&=-\lim_{k\to +\infty}\int_0^{+\infty}(\chi')^{*k}(t)e^{-tP(V+J^u)}( 1, e^{t\mathbf{P}^{*}}(f\nu))\,dt \\&=-\lim_{k\to +\infty}\int_0^{+\infty}(\chi')^{*k}(t)( e^{tX}f, \nu)\,dt. \end{align*} $$
$$ \begin{align*} c(\eta \times \nu)(f)&=( \Pi_0(P(V+J^u))1,f\nu)_{\mathcal H^s \times \mathcal H^{-s}} \\&=-\lim_{k\to +\infty}\int_0^{+\infty}(\chi')^{*k}(t)e^{-tP(V+J^u)}( 1, e^{t\mathbf{P}^{*}}(f\nu))\,dt \\&=-\lim_{k\to +\infty}\int_0^{+\infty}(\chi')^{*k}(t)( e^{tX}f, \nu)\,dt. \end{align*} $$
We use the fact that
![]() $\nu $
is absolutely continuous with respect to
$\nu $
is absolutely continuous with respect to
![]() $\mu _{V+J^u}$
with bounded density to get that
$\mu _{V+J^u}$
with bounded density to get that
![]() $|\nu (e^{tX}f)|\leq C\mu _{V+J^u}(|e^{tX}f|)\leq C\mu _{V+J^u}(|f|)$
because
$|\nu (e^{tX}f)|\leq C\mu _{V+J^u}(|e^{tX}f|)\leq C\mu _{V+J^u}(|f|)$
because
![]() $\mu _{V+J^u}$
is invariant. In particular, we get, by integrating,
$\mu _{V+J^u}$
is invariant. In particular, we get, by integrating,
This proves that the density of
![]() $(\mu \times \nu )$
is invariant by the flow and measurable for the equilibrium state
$(\mu \times \nu )$
is invariant by the flow and measurable for the equilibrium state
![]() $\mu _{V+J^u}$
. However, this last measure is known to be ergodic so the density is constant, which proves the two formulas.
$\mu _{V+J^u}$
. However, this last measure is known to be ergodic so the density is constant, which proves the two formulas.
Weak mixing implies no other resonances on the critical axis. From the averaging formula (8), we see that if
![]() $\nu $
gives zero measure to an invariant Borel set, then it is also the case for
$\nu $
gives zero measure to an invariant Borel set, then it is also the case for
![]() $\mu _{V+J^u}$
and the two measures are actually equivalent.
$\mu _{V+J^u}$
and the two measures are actually equivalent.
Next, we use [Reference Reed and Simon33, Theorem VII.14] to see that the flow is weakly mixing if and only if the only eigenvalue is
![]() $1$
and it is a simple eigenvalue. In other words, if
$1$
and it is a simple eigenvalue. In other words, if
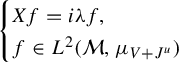 $$ \begin{align} \begin{cases} Xf=i\unicode{x3bb} f, \\ f\in L^2(\mathcal M,\mu_{V+J^u}) \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} Xf=i\unicode{x3bb} f, \\ f\in L^2(\mathcal M,\mu_{V+J^u}) \end{cases} \end{align} $$
has no solution except for
![]() $\unicode{x3bb} =0$
and f constant. Using Proposition 3.1, the presence of another co-resonant state on the critical axis is equivalent to the existence of an absolutely continuous measure with respect to
$\unicode{x3bb} =0$
and f constant. Using Proposition 3.1, the presence of another co-resonant state on the critical axis is equivalent to the existence of an absolutely continuous measure with respect to
![]() $\nu $
. Its density with respect to
$\nu $
. Its density with respect to
![]() $\nu $
is in
$\nu $
is in
![]() $L^{\infty }(\mathcal M,\nu )=L^{\infty }(\mathcal M,\mu _{V+J^u})\subset L^2(\mathcal M,\mu _{V+J^u})$
and is thus a solution of the system above. This shows that weak mixing of the flow with respect to
$L^{\infty }(\mathcal M,\nu )=L^{\infty }(\mathcal M,\mu _{V+J^u})\subset L^2(\mathcal M,\mu _{V+J^u})$
and is thus a solution of the system above. This shows that weak mixing of the flow with respect to
![]() $\mu _{V+J^u}$
implies that there is no other resonance on the critical axis.
$\mu _{V+J^u}$
implies that there is no other resonance on the critical axis.
4 Acting on the bundle of
 $d_s$
-forms
$d_s$
-forms
We have studied the case of
![]() $0$
-forms before and for this, we have fixed a Riemmanian volume
$0$
-forms before and for this, we have fixed a Riemmanian volume
![]() $\mathrm {vol}$
to embed smooth functions into distributions. As a consequence, the co-resonant state
$\mathrm {vol}$
to embed smooth functions into distributions. As a consequence, the co-resonant state
![]() $\nu $
from Theorem 3.1 has a rather convoluted form. Note however that changing the metric does not change the critical axis as the pressure of two cohomologic functions are the same. For
$\nu $
from Theorem 3.1 has a rather convoluted form. Note however that changing the metric does not change the critical axis as the pressure of two cohomologic functions are the same. For
![]() $d_s$
-forms, such an identification is not possible as the bundles involved are not line bundles anymore, and we are led to adopt the more general and intrinsic viewpoint of currents. Loosely speaking, in this new formalism, a distribution is an element of the topological dual of
$d_s$
-forms, such an identification is not possible as the bundles involved are not line bundles anymore, and we are led to adopt the more general and intrinsic viewpoint of currents. Loosely speaking, in this new formalism, a distribution is an element of the topological dual of
![]() $0$
-forms. More generally, we will think of ‘distributions’ on
$0$
-forms. More generally, we will think of ‘distributions’ on
![]() $d_s$
-forms as continuous linear forms on
$d_s$
-forms as continuous linear forms on
![]() $C^{\infty }(\mathcal M, \Lambda ^{d_s}T^{*}\mathcal M)$
and will call this a
$C^{\infty }(\mathcal M, \Lambda ^{d_s}T^{*}\mathcal M)$
and will call this a
![]() $d_s$
-current. The construction of anisotropic Sobolev space is also valid on this space, as noted before in Remark 2.1. (Smoothness is needed to apply the microlocal approach. Here, the bundles
$d_s$
-current. The construction of anisotropic Sobolev space is also valid on this space, as noted before in Remark 2.1. (Smoothness is needed to apply the microlocal approach. Here, the bundles
![]() $E_s^{*}$
and
$E_s^{*}$
and
![]() $E_u^{*}$
are only Hölder continuous but
$E_u^{*}$
are only Hölder continuous but
![]() $\mathscr E_0^k$
is smooth.) We will focus our attention on forms in the kernel of the contraction by the flow, which are given by
$\mathscr E_0^k$
is smooth.) We will focus our attention on forms in the kernel of the contraction by the flow, which are given by
4.1 Critical axis
More generally, the action of
![]() $\mathbf {P}$
will be extended, by duality, to currents. This idea can be traced back at least to Ruelle and Sullivan although no spectral theory was involved in [Reference Ruelle and Sullivan34]. We define a k-current T as a continuous linear form on the space of smooth k-forms. On manifolds, especially when no canonical choice of smooth volume form is available, currents allow us to obtain an intrinsic definition of distributions. As such, the space of smooth k-forms is embedded canonically (up to choosing an orientation) in the space of
$\mathbf {P}$
will be extended, by duality, to currents. This idea can be traced back at least to Ruelle and Sullivan although no spectral theory was involved in [Reference Ruelle and Sullivan34]. We define a k-current T as a continuous linear form on the space of smooth k-forms. On manifolds, especially when no canonical choice of smooth volume form is available, currents allow us to obtain an intrinsic definition of distributions. As such, the space of smooth k-forms is embedded canonically (up to choosing an orientation) in the space of
![]() $(n-k)$
-currents by the formula
$(n-k)$
-currents by the formula
Note that the set of smooth k-forms is dense in the space of homogeneous currents of degree
![]() $n-k$
, see [Reference Chern, Smith and de Rham9, Theorem 12, §15] for a precise statement and more generally [Reference Chern, Smith and de Rham9, Ch. 3] for an introduction to currents. In the rest of the paper, we will write
$n-k$
, see [Reference Chern, Smith and de Rham9, Theorem 12, §15] for a precise statement and more generally [Reference Chern, Smith and de Rham9, Ch. 3] for an introduction to currents. In the rest of the paper, we will write
![]() $\mathcal D' (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
for the space of sections of currents of degree
$\mathcal D' (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
for the space of sections of currents of degree
![]() $d_s$
which are canceled by the contraction
$d_s$
which are canceled by the contraction
![]() $\iota _X$
. They can be thought of as linear combinations of elements of
$\iota _X$
. They can be thought of as linear combinations of elements of
![]() $\Lambda ^{d_u}(E_u^{*}\oplus E_s^{*})$
with distributional coefficients. We first introduce a useful (Hölder continuous) splitting;
$\Lambda ^{d_u}(E_u^{*}\oplus E_s^{*})$
with distributional coefficients. We first introduce a useful (Hölder continuous) splitting;
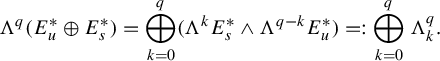 $$ \begin{align} \Lambda^{q}(E_u^{*}\oplus E_s^{*})=\bigoplus_{k=0}^{q} (\Lambda^kE_s^{*}\wedge \Lambda^{q-k}E_u^{*})=:\bigoplus_{k=0}^{q} \Lambda_k^{q}. \end{align} $$
$$ \begin{align} \Lambda^{q}(E_u^{*}\oplus E_s^{*})=\bigoplus_{k=0}^{q} (\Lambda^kE_s^{*}\wedge \Lambda^{q-k}E_u^{*})=:\bigoplus_{k=0}^{q} \Lambda_k^{q}. \end{align} $$
We prove that the system of (unstable) leaf measures
![]() $\{m^u_x\mid x\in \mathcal M\}$
defines a section of currents of Sobolev regularity
$\{m^u_x\mid x\in \mathcal M\}$
defines a section of currents of Sobolev regularity
![]() $\mathcal H^s (\mathcal M; \Lambda ^{d_s}(E_u^{*}\oplus E_s^{*}))$
and is actually a co-resonant state for
$\mathcal H^s (\mathcal M; \Lambda ^{d_s}(E_u^{*}\oplus E_s^{*}))$
and is actually a co-resonant state for
![]() $\unicode{x3bb} =P(V)$
. This point reduces to a computation of the wavefront set of the system of leaf measures
$\unicode{x3bb} =P(V)$
. This point reduces to a computation of the wavefront set of the system of leaf measures
![]() $m^u_V$
by equation (26). This is done by adapting the argument of Lemma 3.2 and we note that the proof is actually easier in this case as we do not have to deal with the smoothness of the unstable Jacobian
$m^u_V$
by equation (26). This is done by adapting the argument of Lemma 3.2 and we note that the proof is actually easier in this case as we do not have to deal with the smoothness of the unstable Jacobian
![]() $J^u$
along the leaves. We will then use the ‘
$J^u$
along the leaves. We will then use the ‘
![]() $L^1$
-norm’ associated to
$L^1$
-norm’ associated to
![]() $m^u_V$
to prove that no Ruelle resonances exist in the half-plane
$m^u_V$
to prove that no Ruelle resonances exist in the half-plane
![]() $\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
by mimicking the proof of Lemma 3.4.
$\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
by mimicking the proof of Lemma 3.4.
However, because we work on forms, the co-resonant state
![]() $m^u_V$
will be non-zero only when tested on sections with values in
$m^u_V$
will be non-zero only when tested on sections with values in
![]() $\Lambda _0^{d_s}$
and will fail to define a norm on the rest of the decomposition. This will explain the need of a more complicated norm, which we will construct in Proposition 4.2.
$\Lambda _0^{d_s}$
and will fail to define a norm on the rest of the decomposition. This will explain the need of a more complicated norm, which we will construct in Proposition 4.2.
More importantly, the decomposition in equation (67) is only Hölder continuous which prevents us from applying the microlocal strategy to obtain a meromorphic extension of the resolvent acting on sections with values in
![]() $\Lambda _k^{d_s}$
.
$\Lambda _k^{d_s}$
.
Indeed, in general, one can only expect to have a Hölder continuous section
![]() ${C^{\alpha }(\mathcal M: \Lambda _k^{d_s})}$
for some
${C^{\alpha }(\mathcal M: \Lambda _k^{d_s})}$
for some
![]() $\alpha>0$
. The pairing against
$\alpha>0$
. The pairing against
![]() $m^u_V$
will however still be justified because the co-resonant state is of order
$m^u_V$
will however still be justified because the co-resonant state is of order
![]() $0$
.
$0$
.
Proposition 4.1. The system of leaf measures
![]() $\{m^u_x\mid x\in \mathcal M\}$
from equation (29) defines a section of
$\{m^u_x\mid x\in \mathcal M\}$
from equation (29) defines a section of
![]() $\mathcal D' (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
, which we will denote by
$\mathcal D' (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
, which we will denote by
![]() $m^u_V$
. Moreover, one has
$m^u_V$
. Moreover, one has
and thus
![]() $m^u_V\in \mathcal H^s (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
and it is a co-resonant state associated to the Ruelle resonance
$m^u_V\in \mathcal H^s (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
and it is a co-resonant state associated to the Ruelle resonance
![]() $P(V)$
. We will call
$P(V)$
. We will call
![]() $P(V)$
the first resonance.
$P(V)$
the first resonance.
Moreover, for any
![]() $1\leq k\leq d_s$
and
$1\leq k\leq d_s$
and
![]() $\omega _k \in C^{\alpha }(\mathcal M; \Lambda _k^{d_s})$
, one has
$\omega _k \in C^{\alpha }(\mathcal M; \Lambda _k^{d_s})$
, one has
![]() $m^u_V(\omega _k)=0$
.
$m^u_V(\omega _k)=0$
.
Proof. Our first goal is to give meaning to
![]() $m^u_V(\varphi )$
for
$m^u_V(\varphi )$
for
![]() $\varphi \in C^{\infty }(\mathcal M; \Lambda ^{d_s}T^{*}\mathcal M)$
. First, the compatibility statement allows us to only define the duality locally, so let
$\varphi \in C^{\infty }(\mathcal M; \Lambda ^{d_s}T^{*}\mathcal M)$
. First, the compatibility statement allows us to only define the duality locally, so let
![]() ${\varphi \in C^{\infty }(\mathcal M; \Lambda ^{d_s}T^{*}\mathcal M)}$
be supported in
${\varphi \in C^{\infty }(\mathcal M; \Lambda ^{d_s}T^{*}\mathcal M)}$
be supported in
![]() $R_q$
. We can define the duality as follows:
$R_q$
. We can define the duality as follows:
 $$ \begin{align} m^u_V(\varphi):=\int_{\mathcal M}m^u_V\wedge \alpha \wedge \varphi=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(x)}e^{w_V^+(y,x)}(\varphi\wedge \alpha)(y)\bigg)\,dm^u_V(x), \end{align} $$
$$ \begin{align} m^u_V(\varphi):=\int_{\mathcal M}m^u_V\wedge \alpha \wedge \varphi=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(x)}e^{w_V^+(y,x)}(\varphi\wedge \alpha)(y)\bigg)\,dm^u_V(x), \end{align} $$
where
![]() $\ \alpha \in E_0^{*}, \ \alpha (X)=1$
. We see that the previous definition makes sense as
$\ \alpha \in E_0^{*}, \ \alpha (X)=1$
. We see that the previous definition makes sense as
![]() $\varphi \wedge \alpha $
is a
$\varphi \wedge \alpha $
is a
![]() $d_s+1$
form and as
$d_s+1$
form and as
![]() $w_V^+(x,y)$
is smooth in y, in the sense of Lemma 3.2, and continuous in x. The formula clearly defines a current of degree
$w_V^+(x,y)$
is smooth in y, in the sense of Lemma 3.2, and continuous in x. The formula clearly defines a current of degree
![]() $0$
so
$0$
so
![]() $m^u_V\in D' (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
.
$m^u_V\in D' (\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
.
Let
![]() $\omega _k \in C^{\alpha }(\mathcal M: \Lambda _k^{d_s})$
for some k. Then, the fact that
$\omega _k \in C^{\alpha }(\mathcal M: \Lambda _k^{d_s})$
for some k. Then, the fact that
![]() $m^u_V$
is a measure on
$m^u_V$
is a measure on
![]() $\mathcal W^u(q,\delta )$
shows that the pairing
$\mathcal W^u(q,\delta )$
shows that the pairing
![]() $m^u_V(\omega _k)$
is well defined. If
$m^u_V(\omega _k)$
is well defined. If
![]() $k\geq 1$
, we can use equation (62) and the definition of
$k\geq 1$
, we can use equation (62) and the definition of
![]() $E_s^{*}$
to get that
$E_s^{*}$
to get that
![]() $m^u_V(\omega _k)=0$
.
$m^u_V(\omega _k)=0$
.
To prove the first part of equation (61), we can consider a
![]() $d_s$
form
$d_s$
form
![]() $\varphi $
supported in
$\varphi $
supported in
![]() $R_q$
such that
$R_q$
such that
![]() $e^{-t\mathbf {P}}\varphi $
is also supported in
$e^{-t\mathbf {P}}\varphi $
is also supported in
![]() $R_q$
. We have to prove that
$R_q$
. We have to prove that
![]() $m^u_V(e^{t\mathbf {P}}\varphi )=e^{tP(V)}m^u_V(\varphi )$
. We first use the Leibniz rule to get
$m^u_V(e^{t\mathbf {P}}\varphi )=e^{tP(V)}m^u_V(\varphi )$
. We first use the Leibniz rule to get
![]() $\mathcal L_X(\varphi \wedge \alpha )=\mathcal L_X\varphi \wedge \alpha +\varphi \wedge \mathcal L_X\alpha =\mathcal L_X\varphi \wedge \alpha. $
This allows us to compute explicitly the action of the propagator on the current
$\mathcal L_X(\varphi \wedge \alpha )=\mathcal L_X\varphi \wedge \alpha +\varphi \wedge \mathcal L_X\alpha =\mathcal L_X\varphi \wedge \alpha. $
This allows us to compute explicitly the action of the propagator on the current
![]() $m^u_V$
. More precisely, we use the cocycle relation in equation (34), equation (33), as well as
$m^u_V$
. More precisely, we use the cocycle relation in equation (34), equation (33), as well as
![]() $\varphi _t$
conformality in equation (30):
$\varphi _t$
conformality in equation (30):
 $$ \begin{align*} &m^u_V(e^{t\mathbf{P}}\varphi)=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(x)}e^{w_V^+(y,x)}e^{S_tV(\varphi_{-t}y)}e^{t\mathcal L_{{X}}} (\varphi \wedge \alpha)(y)\bigg)\,dm^u_V(x) \\&\quad=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(\varphi_tx )}e^{w_V^+(\varphi_t w,x)}e^{S_tV(w)}(\varphi \wedge \alpha)(w)\bigg)\,dm^u_V(x) \\&\quad=\int_{\mathcal W^u(q,\delta)}\!\!e^{w_V^+(\varphi_t x,x)}\bigg(\!\int_{R_q^{ws}(\varphi_t x )}\!\! e^{w_V^+(\varphi_t w,w)}e^{w_V^+(w,\varphi_tx)}e^{S_tV(w)}(\varphi \wedge \alpha)(w)\bigg)\,dm^u_V(x) \\&\quad=\int_{\mathcal W^u(q,\delta)}e^{2tP(V)}e^{-S_tV(x)}\bigg(\!\int_{R_q^{ws}(\varphi_t x )}e^{w_V^+(w,\varphi_tx)}(\varphi \wedge \alpha)(w)\bigg)\,dm^u_V(x) \\&\quad=e^{tP(V)}\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(z )} e^{w_V^+(z,w)} (\varphi \wedge \alpha)(z)\bigg)\,dm^u_V(z)=e^{tP(V)}m^u_V(\varphi). \end{align*} $$
$$ \begin{align*} &m^u_V(e^{t\mathbf{P}}\varphi)=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(x)}e^{w_V^+(y,x)}e^{S_tV(\varphi_{-t}y)}e^{t\mathcal L_{{X}}} (\varphi \wedge \alpha)(y)\bigg)\,dm^u_V(x) \\&\quad=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(\varphi_tx )}e^{w_V^+(\varphi_t w,x)}e^{S_tV(w)}(\varphi \wedge \alpha)(w)\bigg)\,dm^u_V(x) \\&\quad=\int_{\mathcal W^u(q,\delta)}\!\!e^{w_V^+(\varphi_t x,x)}\bigg(\!\int_{R_q^{ws}(\varphi_t x )}\!\! e^{w_V^+(\varphi_t w,w)}e^{w_V^+(w,\varphi_tx)}e^{S_tV(w)}(\varphi \wedge \alpha)(w)\bigg)\,dm^u_V(x) \\&\quad=\int_{\mathcal W^u(q,\delta)}e^{2tP(V)}e^{-S_tV(x)}\bigg(\!\int_{R_q^{ws}(\varphi_t x )}e^{w_V^+(w,\varphi_tx)}(\varphi \wedge \alpha)(w)\bigg)\,dm^u_V(x) \\&\quad=e^{tP(V)}\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(z )} e^{w_V^+(z,w)} (\varphi \wedge \alpha)(z)\bigg)\,dm^u_V(z)=e^{tP(V)}m^u_V(\varphi). \end{align*} $$
For the wavefront set condition, we mimic the argument of Lemma 3.2, and consider a smooth
![]() $d_s$
-form
$d_s$
-form
![]() $\chi $
supported in
$\chi $
supported in
![]() $R_q$
and S a phase function such that
$R_q$
and S a phase function such that
![]() $dS(q)=\xi \notin E_s^{*}$
, and compute
$dS(q)=\xi \notin E_s^{*}$
, and compute
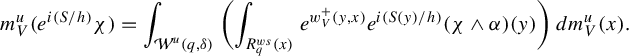 $$ \begin{align*} m^u_V(e^{i(S/h)}\chi)=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(x)}e^{w_V^+(y,x)}e^{i({S(y)}/h)}(\chi\wedge \alpha)(y)\bigg)\,dm^u_V(x).\end{align*} $$
$$ \begin{align*} m^u_V(e^{i(S/h)}\chi)=\int_{\mathcal W^u(q,\delta)}\bigg(\!\int_{R_q^{ws}(x)}e^{w_V^+(y,x)}e^{i({S(y)}/h)}(\chi\wedge \alpha)(y)\bigg)\,dm^u_V(x).\end{align*} $$
Now, the proof is easier than for Lemma 3.2 as the integrand is easily seen to be smooth along the weak-stable leaves (because the potential V is smooth) uniformly in x. We can perform integration by parts and show that the integrand is
![]() $O(h^{\infty })$
as long as
$O(h^{\infty })$
as long as
![]() $dS$
does not vanish on
$dS$
does not vanish on
![]() $R_q^{ws}(x)$
, which can be ensured near q by the definition of
$R_q^{ws}(x)$
, which can be ensured near q by the definition of
![]() $E_s^{*}$
. This shows that
$E_s^{*}$
. This shows that
![]() $\xi \notin \mathrm {WF}(m^u_V)$
and thus
$\xi \notin \mathrm {WF}(m^u_V)$
and thus
![]() $ \mathrm {WF}(m^u_V)\subset E_s^{*}$
. This shows that
$ \mathrm {WF}(m^u_V)\subset E_s^{*}$
. This shows that
![]() $P(V)$
is a Ruelle resonance with the associated Ruelle co-resonant state given by
$P(V)$
is a Ruelle resonance with the associated Ruelle co-resonant state given by
![]() $m^u_V$
.
$m^u_V$
.
If we consider the adjoint
![]() $\mathbf {P}^{*}$
, the above theorem would give that
$\mathbf {P}^{*}$
, the above theorem would give that
![]() $m^s_V$
is a resonant state for
$m^s_V$
is a resonant state for
![]() $P(V)$
. We also get a product construction of the equilibrium measure. In this case, it is actually easier than in the case of functions, as the product is given by the usual wedge product (extended to distributions with convenient wavefront sets). The following lemma is a re-writing of [Reference Climenhaga10, Theorem 3.10] and corresponds to the second part of Theorem 1.2.
$P(V)$
. We also get a product construction of the equilibrium measure. In this case, it is actually easier than in the case of functions, as the product is given by the usual wedge product (extended to distributions with convenient wavefront sets). The following lemma is a re-writing of [Reference Climenhaga10, Theorem 3.10] and corresponds to the second part of Theorem 1.2.
Lemma 4.1. (Equilibrium state as a product)
There exists
![]() $c>0$
such that
$c>0$
such that
Similarly to the case of functions, we now prove that
![]() $\{\mathrm {Re}(\unicode{x3bb} )=P(V)\}$
is the critical axis by using the ‘
$\{\mathrm {Re}(\unicode{x3bb} )=P(V)\}$
is the critical axis by using the ‘
![]() $L^1$
-norm’ associated to the co-resonant state
$L^1$
-norm’ associated to the co-resonant state
![]() $m^u_V$
. Nevertheless, because we work on forms, the following norm will only be non-zero for a section with values in
$m^u_V$
. Nevertheless, because we work on forms, the following norm will only be non-zero for a section with values in
![]() $ \Lambda _0^{d_s}$
.
$ \Lambda _0^{d_s}$
.
Lemma 4.2. We define a norm on
![]() $C^{0}(\mathcal M; \Lambda _0^{d_s})$
by posing
$C^{0}(\mathcal M; \Lambda _0^{d_s})$
by posing
This norm satisfies the bound
Proof. Suppose
![]() $\varphi \in C^{0}(\mathcal M;\Lambda ^{d_s}_0)$
, the bundle is one-dimensional and it thus makes sense to talk of
$\varphi \in C^{0}(\mathcal M;\Lambda ^{d_s}_0)$
, the bundle is one-dimensional and it thus makes sense to talk of
![]() $|\varphi |\wedge \alpha $
as a
$|\varphi |\wedge \alpha $
as a
![]() $d_s+1$
density. If
$d_s+1$
density. If
![]() $\varphi (q)\neq 0$
, then by continuity,
$\varphi (q)\neq 0$
, then by continuity,
![]() $\varphi \neq 0$
on a small open set. Then,
$\varphi \neq 0$
on a small open set. Then,
![]() $\|\varphi \|_{V,0}>0$
because
$\|\varphi \|_{V,0}>0$
because
![]() $m^u_V$
gives a positive measure to any open set. The bound in equation (64) follows from the fact that
$m^u_V$
gives a positive measure to any open set. The bound in equation (64) follows from the fact that
![]() $m^u _V$
is a co-resonant state. The last point follows from the first two points by a direct adaptation of the proof of Lemma 3.4.
$m^u _V$
is a co-resonant state. The last point follows from the first two points by a direct adaptation of the proof of Lemma 3.4.
Remark 4.1. The one-dimensional nature of
![]() $\Lambda _0^{d_s}$
will be crucial to obtain a fine description of the resonant states on the critical axis. Recall that in the proof of Proposition 3.1, it was shown that the space of resonant states was given by
$\Lambda _0^{d_s}$
will be crucial to obtain a fine description of the resonant states on the critical axis. Recall that in the proof of Proposition 3.1, it was shown that the space of resonant states was given by
![]() $\Pi _0(C^{\infty })$
and that
$\Pi _0(C^{\infty })$
and that
![]() $u\leq Cv$
implied that
$u\leq Cv$
implied that
![]() $\Pi _0(u)$
was absolutely continuous with respect to
$\Pi _0(u)$
was absolutely continuous with respect to
![]() $\Pi _0(v).$
One could then deduce the simplicity of the first resonance from the ergodicity of the flow and the non-presence of other resonances on the critical axis by the mixing properties of the flow. Here, we will use a similar approach by showing that the set of resonant states is given by
$\Pi _0(v).$
One could then deduce the simplicity of the first resonance from the ergodicity of the flow and the non-presence of other resonances on the critical axis by the mixing properties of the flow. Here, we will use a similar approach by showing that the set of resonant states is given by
![]() $\Pi _0(\Lambda _0^{d_s}).$
$\Pi _0(\Lambda _0^{d_s}).$
We now use this norm and a ‘shift’ to define inductively a norm on
![]() $C^0(\mathcal M; \Lambda _k^{d_s})$
for any k. We use Assumption 1 to define the set of (normalized) trivialization of
$C^0(\mathcal M; \Lambda _k^{d_s})$
for any k. We use Assumption 1 to define the set of (normalized) trivialization of
![]() $E_u$
:
$E_u$
:
and its dual counterpart
Proposition 4.2. We define a norm inductively on
![]() $C^0(\mathcal M; \Lambda _{k}^{d_s}), k\geq 1$
, by posing, for
$C^0(\mathcal M; \Lambda _{k}^{d_s}), k\geq 1$
, by posing, for
![]() $f \in C^{0}(\mathcal M; \Lambda _k^{d_s})$
,
$f \in C^{0}(\mathcal M; \Lambda _k^{d_s})$
,
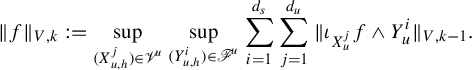 $$ \begin{align} \|f\|_{V,k}:= \sup_{(X^j_{u,h})\in \mathscr V^u}\sup_{(Y^i_{u,h})\in \mathscr F^u}\sum_{i=1}^{d_s}\sum_{j=1}^{d_u}\|\iota_{X_u^j}f\wedge Y_u^{i}\|_{V,k-1}. \end{align} $$
$$ \begin{align} \|f\|_{V,k}:= \sup_{(X^j_{u,h})\in \mathscr V^u}\sup_{(Y^i_{u,h})\in \mathscr F^u}\sum_{i=1}^{d_s}\sum_{j=1}^{d_u}\|\iota_{X_u^j}f\wedge Y_u^{i}\|_{V,k-1}. \end{align} $$
This norm satisfies the bound
for some
![]() $C,\eta>0$
. As a consequence, there are no Ruelle resonances in
$C,\eta>0$
. As a consequence, there are no Ruelle resonances in
![]() $\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
and if
$\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
and if
![]() $\unicode{x3bb} $
is a Ruelle resonance on the critical axis, then it has no Jordan block.
$\unicode{x3bb} $
is a Ruelle resonance on the critical axis, then it has no Jordan block.
Proof. Contracting with a vector in
![]() $E_u$
and then wedging with a vector in
$E_u$
and then wedging with a vector in
![]() $E_u^{*}$
sends a section of
$E_u^{*}$
sends a section of
![]() $C^0(\mathcal M; \Lambda _{k}^{d_s})$
to
$C^0(\mathcal M; \Lambda _{k}^{d_s})$
to
![]() $C^0(\mathcal M; \Lambda _{k-1}^{d_s})$
, so the formula makes sense by induction. Let us prove that the norm takes finite values. For this, we use the fact that
$C^0(\mathcal M; \Lambda _{k-1}^{d_s})$
, so the formula makes sense by induction. Let us prove that the norm takes finite values. For this, we use the fact that
![]() $m^u_V$
is of order zero and Lemma 4.2 to get first that for
$m^u_V$
is of order zero and Lemma 4.2 to get first that for
![]() $f\in C^0(\mathcal M; \Lambda _{0}^{d_s})$
, one has
$f\in C^0(\mathcal M; \Lambda _{0}^{d_s})$
, one has
![]() $\|f\|_{V,0}\leq C\|f\|_0$
. This implies, for any
$\|f\|_{V,0}\leq C\|f\|_0$
. This implies, for any
![]() $f\in C^0(\mathcal M; \Lambda _{1}^{d_s})$
,
$f\in C^0(\mathcal M; \Lambda _{1}^{d_s})$
,
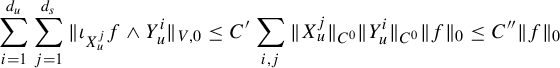 $$ \begin{align*} \sum_{i=1}^{d_u}\sum_{j=1}^{d_s}\|\iota_{X_u^j}f\wedge Y_u^{i}\|_{V,0}\leq C'\sum_{i,j}\|X_u^j\|_{C^0}\|Y_u^i\|_{C^0}\|f\|_0\leq C"\|f\|_0 \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{d_u}\sum_{j=1}^{d_s}\|\iota_{X_u^j}f\wedge Y_u^{i}\|_{V,0}\leq C'\sum_{i,j}\|X_u^j\|_{C^0}\|Y_u^i\|_{C^0}\|f\|_0\leq C"\|f\|_0 \end{align*} $$
with a constant
![]() $C"$
independent of the choice of cover or partition of unity. This shows that
$C"$
independent of the choice of cover or partition of unity. This shows that
![]() $\|.\|_{V,1}$
takes finite values and a quick induction shows that it is also the case of
$\|.\|_{V,1}$
takes finite values and a quick induction shows that it is also the case of
![]() $\|.\|_{V,k}$
for any k. The triangle inequality, homogeneity, and non-negativity of
$\|.\|_{V,k}$
for any k. The triangle inequality, homogeneity, and non-negativity of
![]() $\|.\|_{V,k}$
follow from Lemma 4.2 and an induction. Suppose now that
$\|.\|_{V,k}$
follow from Lemma 4.2 and an induction. Suppose now that
![]() $f \in C^0(\mathcal M; \Lambda _{k}^{d_s})$
and
$f \in C^0(\mathcal M; \Lambda _{k}^{d_s})$
and
![]() $f\neq 0$
. Then, f is non-zero on a small open set, and since
$f\neq 0$
. Then, f is non-zero on a small open set, and since
![]() $(X_{s,h}^j)$
and
$(X_{s,h}^j)$
and
![]() $(Y_u^i)$
are local bases, then there is
$(Y_u^i)$
are local bases, then there is
![]() $(i_0,j_0)$
such that
$(i_0,j_0)$
such that
![]() $\iota _{X_{s,h}^{j_0}}f\wedge Y_u^{i_0}$
is continuous and non-zero on that open set. By induction and the fact that
$\iota _{X_{s,h}^{j_0}}f\wedge Y_u^{i_0}$
is continuous and non-zero on that open set. By induction and the fact that
![]() $m^u_V$
gives a positive measure to any non-empty open set, we get that
$m^u_V$
gives a positive measure to any non-empty open set, we get that
![]() $\|f\|_{V,k}>0$
and
$\|f\|_{V,k}>0$
and
![]() $\|.\|_{V,k}$
thus defines a norm. We prove equation (66):
$\|.\|_{V,k}$
thus defines a norm. We prove equation (66):
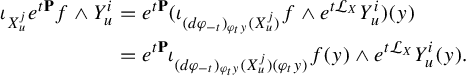 $$ \begin{align*} \iota_{X_u^j}e^{t\mathbf{P}}f\wedge Y_u^{i}&=e^{t\mathbf{P}}( \iota_{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)}f\wedge e^{t\mathcal L_X}Y_u^{i})(y) \\&=e^{t\mathbf{P}}\iota_{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)(\varphi_t y)}f(y)\wedge e^{t\mathcal L_X}Y_u^{i}(y). \end{align*} $$
$$ \begin{align*} \iota_{X_u^j}e^{t\mathbf{P}}f\wedge Y_u^{i}&=e^{t\mathbf{P}}( \iota_{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)}f\wedge e^{t\mathcal L_X}Y_u^{i})(y) \\&=e^{t\mathbf{P}}\iota_{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)(\varphi_t y)}f(y)\wedge e^{t\mathcal L_X}Y_u^{i}(y). \end{align*} $$
Using the invariance of the Anosov decomposition in equation (13), we get
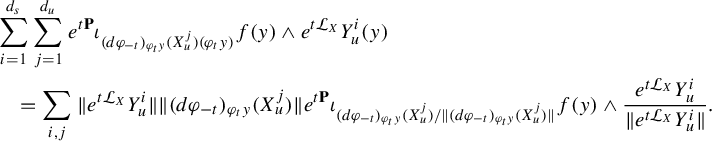 $$ \begin{align*} &\sum_{i=1}^{d_s}\sum_{j=1}^{d_u}e^{t\mathbf{P}}\iota_{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)(\varphi_t y)}f(y)\wedge e^{t\mathcal L_X}Y_u^{i}(y) \\ &\quad =\sum_{i,j}\|e^{t\mathcal L_X}Y_u^{i}\|\|(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)\| e^{t\mathbf{P}}\iota_{{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)}/{\|(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)\|}}f(y)\wedge \frac{e^{t\mathcal L_X}Y_u^{i}}{\|e^{t\mathcal L_X}Y_u^{i}\|}. \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^{d_s}\sum_{j=1}^{d_u}e^{t\mathbf{P}}\iota_{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)(\varphi_t y)}f(y)\wedge e^{t\mathcal L_X}Y_u^{i}(y) \\ &\quad =\sum_{i,j}\|e^{t\mathcal L_X}Y_u^{i}\|\|(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)\| e^{t\mathbf{P}}\iota_{{(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)}/{\|(d\varphi_{-t})_{\varphi_{t}y}(X_u^j)\|}}f(y)\wedge \frac{e^{t\mathcal L_X}Y_u^{i}}{\|e^{t\mathcal L_X}Y_u^{i}\|}. \end{align*} $$
We then have
![]() $\|e^{t\mathcal L_X}Y_u^{i}\|,\|(d\varphi _{-t})_{\varphi _{t}y}(X_u^j)\|\leq Ce^{-t\eta }$
for some (uniform)
$\|e^{t\mathcal L_X}Y_u^{i}\|,\|(d\varphi _{-t})_{\varphi _{t}y}(X_u^j)\|\leq Ce^{-t\eta }$
for some (uniform)
![]() $C,\eta>0$
by the Anosov property. Finally, we obtain
$C,\eta>0$
by the Anosov property. Finally, we obtain
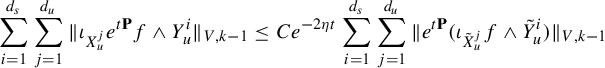 $$ \begin{align*} \sum_{i=1}^{d_s}\sum_{j=1}^{d_u}\|\iota_{X_u^j}e^{t\mathbf{P}}f\wedge Y_u^{i}\|_{V,k-1}\leq Ce^{-2\eta t} \sum_{i=1}^{d_s}\sum_{j=1}^{d_u} \|e^{t\mathbf{P}}(\iota_{\tilde X_u^j}f\wedge \tilde Y_u^{i})\|_{V,k-1} \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{d_s}\sum_{j=1}^{d_u}\|\iota_{X_u^j}e^{t\mathbf{P}}f\wedge Y_u^{i}\|_{V,k-1}\leq Ce^{-2\eta t} \sum_{i=1}^{d_s}\sum_{j=1}^{d_u} \|e^{t\mathbf{P}}(\iota_{\tilde X_u^j}f\wedge \tilde Y_u^{i})\|_{V,k-1} \end{align*} $$
for
![]() $\tilde X_u^j:=(d\varphi _{-t})_{\varphi _{t}y}(X_u^j)/\|(d\varphi _{-t})_{\varphi _{t}y}(X_u^j)\|$
and
$\tilde X_u^j:=(d\varphi _{-t})_{\varphi _{t}y}(X_u^j)/\|(d\varphi _{-t})_{\varphi _{t}y}(X_u^j)\|$
and
![]() $\tilde Y_u^{i}=e^{t\mathcal L_X}Y_u^{i}/\|e^{t\mathcal L_X}Y_u^{i}\|$
. Passing to the supremum thus gives
$\tilde Y_u^{i}=e^{t\mathcal L_X}Y_u^{i}/\|e^{t\mathcal L_X}Y_u^{i}\|$
. Passing to the supremum thus gives
To conclude the proof of equation (66), we only need to initialize the induction, and this is exactly the statement of Lemma 4.2.
Consider
![]() $f\in C^{\infty }(\mathcal M; \mathscr E_{d_s})$
and consider its decomposition
$f\in C^{\infty }(\mathcal M; \mathscr E_{d_s})$
and consider its decomposition
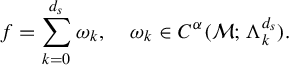 $$ \begin{align*}f= \sum_{k=0}^{d_s} \omega_k, \quad \omega_k \in C^{\alpha}(\mathcal M; \Lambda_k^{d_s}). \end{align*} $$
$$ \begin{align*}f= \sum_{k=0}^{d_s} \omega_k, \quad \omega_k \in C^{\alpha}(\mathcal M; \Lambda_k^{d_s}). \end{align*} $$
We define a norm on
![]() $C^{\infty }(\mathcal M; \mathscr E_{d_s})$
with the following bound when using the propagator:
$C^{\infty }(\mathcal M; \mathscr E_{d_s})$
with the following bound when using the propagator:
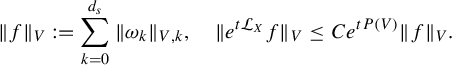 $$ \begin{align*}\|f\|_{V}:=\sum_{k=0}^{d_s}\|\omega_k\|_{V,k}, \quad \|e^{t\mathcal L_X}f\|_V\leq Ce^{tP(V)}\|f\|_V.\end{align*} $$
$$ \begin{align*}\|f\|_{V}:=\sum_{k=0}^{d_s}\|\omega_k\|_{V,k}, \quad \|e^{t\mathcal L_X}f\|_V\leq Ce^{tP(V)}\|f\|_V.\end{align*} $$
This is the only thing we need to mimic the argument of Lemmas 3.4 and 3.5, and prove that no resonance exists in
![]() $\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
and that resonances on the critical axis have no Jordan block.
$\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
and that resonances on the critical axis have no Jordan block.
We will now prove Theorem 1.1 for the action on
![]() $d_s$
-forms.
$d_s$
-forms.
Proposition 4.3. (Critical axis for
 $d_s$
-forms)
$d_s$
-forms)
Under Assumption 1, the first resonance
![]() $P(V)$
is simple and the space of co-resonant states is spanned by
$P(V)$
is simple and the space of co-resonant states is spanned by
![]() $m^u_V$
.
$m^u_V$
.
Proof. The argument of Lemma 3.6 goes through and the projector
![]() $ \Pi _0(\unicode{x3bb} )$
on the resonant states is obtained as the limit of
$ \Pi _0(\unicode{x3bb} )$
on the resonant states is obtained as the limit of
![]() $\tilde R(\unicode{x3bb} )^n$
as an operator
$\tilde R(\unicode{x3bb} )^n$
as an operator
![]() $\mathcal H^s \to \mathcal H^s$
. The formula defining
$\mathcal H^s \to \mathcal H^s$
. The formula defining
![]() $\tilde R(\unicode{x3bb} )$
is the same. In particular, as in the proof of Proposition 3.1, we obtain every co-resonant state by the following construction:
$\tilde R(\unicode{x3bb} )$
is the same. In particular, as in the proof of Proposition 3.1, we obtain every co-resonant state by the following construction:
where the convergence holds in
![]() $\mathcal H^s$
. Consider the pairing between
$\mathcal H^s$
. Consider the pairing between
![]() $C^{\infty }(\mathcal M; \Lambda ^{d_s}(E_u^{*}\oplus E_s^{*}))$
and
$C^{\infty }(\mathcal M; \Lambda ^{d_s}(E_u^{*}\oplus E_s^{*}))$
and
![]() $C^{\infty }(\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
defined by
$C^{\infty }(\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
defined by
![]() $\langle v, u\rangle :=\int _{\mathcal M}u\wedge \alpha \wedge v,$
extended to
$\langle v, u\rangle :=\int _{\mathcal M}u\wedge \alpha \wedge v,$
extended to
![]() ${\mathcal H^s\times \mathcal H^{-s}}$
.
${\mathcal H^s\times \mathcal H^{-s}}$
.
Co-resonant states define currents of order 0. Consider two smooth forms
![]() ${\omega \in C^{\infty }(\mathcal M; \Lambda ^{d_s}(E_u^{*}\oplus E_s^{*}))}$
and
${\omega \in C^{\infty }(\mathcal M; \Lambda ^{d_s}(E_u^{*}\oplus E_s^{*}))}$
and
![]() $\theta \in C^{\infty }(\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
. We first expand these forms:
$\theta \in C^{\infty }(\mathcal M; \Lambda ^{d_u}(E_u^{*}\oplus E_s^{*}))$
. We first expand these forms:
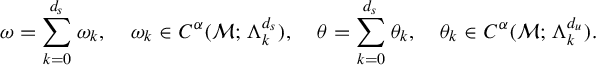 $$ \begin{align} \omega=\sum_{k=0}^{d_s}\omega_k,\quad \omega_k\in C^{\alpha}(\mathcal M; \Lambda_k^{d_s}), \quad \theta=\sum_{k=0}^{d_s}\theta_k,\quad \theta_k\in C^{\alpha}(\mathcal M; \Lambda_k^{d_u}). \end{align} $$
$$ \begin{align} \omega=\sum_{k=0}^{d_s}\omega_k,\quad \omega_k\in C^{\alpha}(\mathcal M; \Lambda_k^{d_s}), \quad \theta=\sum_{k=0}^{d_s}\theta_k,\quad \theta_k\in C^{\alpha}(\mathcal M; \Lambda_k^{d_u}). \end{align} $$
Note that the regularity of the component is only Hölder continuous here because of the regularity of the stable and unstable foliation. We see that
![]() $\omega _k\wedge \alpha \wedge \theta _l$
is a continuous n-form which is non-zero if and only if
$\omega _k\wedge \alpha \wedge \theta _l$
is a continuous n-form which is non-zero if and only if
![]() $k+l=d_s$
. The previous discussion justifies the following convergence:
$k+l=d_s$
. The previous discussion justifies the following convergence:
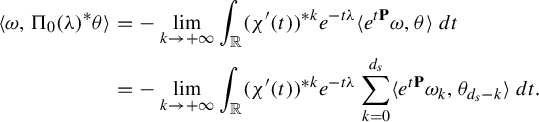 $$ \begin{align*} \langle \omega, \Pi_0(\unicode{x3bb})^{*}\theta\rangle&=-\lim_{k\to+\infty}\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega, \theta\rangle\,dt \\&=- \lim_{k\to+\infty}\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\sum_{k=0}^{d_s}\langle e^{t\mathbf P}\omega_k, \theta_{d_s-k}\rangle\,dt. \end{align*} $$
$$ \begin{align*} \langle \omega, \Pi_0(\unicode{x3bb})^{*}\theta\rangle&=-\lim_{k\to+\infty}\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega, \theta\rangle\,dt \\&=- \lim_{k\to+\infty}\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\sum_{k=0}^{d_s}\langle e^{t\mathbf P}\omega_k, \theta_{d_s-k}\rangle\,dt. \end{align*} $$
Here, we have noticed that the integration over all the manifold is an n-current of order zero and thus extends to continuous n-forms.
By Assumption 1, we can find a trivialization basis
![]() $(Y^j_{u})_{1\leq j \leq d_s}\in C^0(\mathcal M; E_u^{*})$
such that
$(Y^j_{u})_{1\leq j \leq d_s}\in C^0(\mathcal M; E_u^{*})$
such that
![]() $ E_u^{*}=\mathrm {Span}\{Y^j_{u}, \ 1\leq j \leq d_s\}$
and
$ E_u^{*}=\mathrm {Span}\{Y^j_{u}, \ 1\leq j \leq d_s\}$
and
![]() $(Y^j_{s})_{1\leq j \leq d_u}\in C^0(\mathcal M; E_s^{*})$
such that
$(Y^j_{s})_{1\leq j \leq d_u}\in C^0(\mathcal M; E_s^{*})$
such that
![]() $ {E_s^{*}=\mathrm {Span}\{Y^j_{s}, \ 1\leq j \leq d_u\}}$
. Let
$ {E_s^{*}=\mathrm {Span}\{Y^j_{s}, \ 1\leq j \leq d_u\}}$
. Let
![]() $Y_s^1\wedge \cdots \wedge Y_s^{d_s}\wedge \alpha \wedge Y_s^1\wedge \cdots \wedge Y_s^{d_u}=: \tilde \omega \wedge \alpha \wedge \tilde \theta $
be a non-vanishing continuous n-form which we suppose to be positive. We notice to start that, using the Anosov property, there is an
$Y_s^1\wedge \cdots \wedge Y_s^{d_s}\wedge \alpha \wedge Y_s^1\wedge \cdots \wedge Y_s^{d_u}=: \tilde \omega \wedge \alpha \wedge \tilde \theta $
be a non-vanishing continuous n-form which we suppose to be positive. We notice to start that, using the Anosov property, there is an
![]() $\eta>0$
such that
$\eta>0$
such that
 $$ \begin{align*} \int_{\mathcal M}|&e^{t\mathbf{P}}(Y_u^1\wedge \cdots Y_u^{d_s-1}\wedge Y_s^1)\wedge \alpha \wedge Y_u^{d_s}\wedge Y_s^2\wedge \cdots \wedge Y_s^{d_s}| \\&\leq Ce^{-t\eta}\int_{\mathcal M}|e^{t\mathbf{P}}(Y_u^1\wedge \cdots Y_u^{d_s-1})\wedge \alpha \wedge Y_u^{d_s}\wedge Y_s^1\wedge Y_s^2\wedge \cdots \wedge Y_s^{d_s}| \\&\leq Ce^{-2t\eta}\int_{\mathcal M}|e^{t\mathbf{P}}(Y_u^1\wedge \cdots Y_u^{d_s-1} \wedge Y_u^{d_s})\wedge \alpha \wedge Y_s^1\wedge Y_s^2\wedge \cdots \wedge Y_s^{d_s}| \\&\leq Ce^{-2t\eta}\int_{\mathcal M}e^{t\mathbf P}(\tilde \omega) \wedge \alpha \wedge \tilde \theta. \end{align*} $$
$$ \begin{align*} \int_{\mathcal M}|&e^{t\mathbf{P}}(Y_u^1\wedge \cdots Y_u^{d_s-1}\wedge Y_s^1)\wedge \alpha \wedge Y_u^{d_s}\wedge Y_s^2\wedge \cdots \wedge Y_s^{d_s}| \\&\leq Ce^{-t\eta}\int_{\mathcal M}|e^{t\mathbf{P}}(Y_u^1\wedge \cdots Y_u^{d_s-1})\wedge \alpha \wedge Y_u^{d_s}\wedge Y_s^1\wedge Y_s^2\wedge \cdots \wedge Y_s^{d_s}| \\&\leq Ce^{-2t\eta}\int_{\mathcal M}|e^{t\mathbf{P}}(Y_u^1\wedge \cdots Y_u^{d_s-1} \wedge Y_u^{d_s})\wedge \alpha \wedge Y_s^1\wedge Y_s^2\wedge \cdots \wedge Y_s^{d_s}| \\&\leq Ce^{-2t\eta}\int_{\mathcal M}e^{t\mathbf P}(\tilde \omega) \wedge \alpha \wedge \tilde \theta. \end{align*} $$
Thus, a quick induction yields the following bound:
Now, choose a smooth section
![]() $\omega $
and
$\omega $
and
![]() $\theta $
such that
$\theta $
such that
![]() $\omega _0$
and
$\omega _0$
and
![]() $\theta _{d_s}$
are non-vanishing on
$\theta _{d_s}$
are non-vanishing on
![]() $\mathcal M$
. Note that such an
$\mathcal M$
. Note that such an
![]() $\omega $
can be obtained by approximating in
$\omega $
can be obtained by approximating in
![]() $C^0$
norm a non-vanishing continuous section by smooth sections. Then, we get the convergence of
$C^0$
norm a non-vanishing continuous section by smooth sections. Then, we get the convergence of
Consider thus an arbitrary
![]() $\epsilon>0$
and an integer
$\epsilon>0$
and an integer
![]() $k_0\geq 0$
such that for any
$k_0\geq 0$
such that for any
![]() $k\geq k_0$
, one has
$k\geq k_0$
, one has
 $$ \begin{align*}-\epsilon \leq \bigg|\!\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega_0, \theta_0\rangle(1+O(e^{-\eta t}))\,dt+\ell\bigg| \leq \epsilon. \end{align*} $$
$$ \begin{align*}-\epsilon \leq \bigg|\!\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega_0, \theta_0\rangle(1+O(e^{-\eta t}))\,dt+\ell\bigg| \leq \epsilon. \end{align*} $$
The support of the
![]() $(\chi '(t))^{*k}$
goes to infinity with k, so we can suppose that for
$(\chi '(t))^{*k}$
goes to infinity with k, so we can suppose that for
![]() $k\geq k_0$
, one has
$k\geq k_0$
, one has
![]() $ 1-\epsilon \leq 1+O(e^{-\eta t})\leq 1+\epsilon $
on the support of the integrand. In other words, we have obtained
$ 1-\epsilon \leq 1+O(e^{-\eta t})\leq 1+\epsilon $
on the support of the integrand. In other words, we have obtained
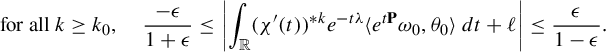 $$ \begin{align*}\text{ for all } k\geq k_0, \quad \frac{-\epsilon}{1+\epsilon} \leq \bigg|\!\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega_0, \theta_0\rangle\,dt+\ell\bigg|\leq \frac{\epsilon}{1-\epsilon}. \end{align*} $$
$$ \begin{align*}\text{ for all } k\geq k_0, \quad \frac{-\epsilon}{1+\epsilon} \leq \bigg|\!\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega_0, \theta_0\rangle\,dt+\ell\bigg|\leq \frac{\epsilon}{1-\epsilon}. \end{align*} $$
This also proves the boundedness of the above integral with
![]() $\omega _0$
and
$\omega _0$
and
![]() $\theta _0$
replaced by
$\theta _0$
replaced by
![]() $\tilde \omega $
and
$\tilde \omega $
and
![]() $\tilde \theta $
, and this shows that
$\tilde \theta $
, and this shows that
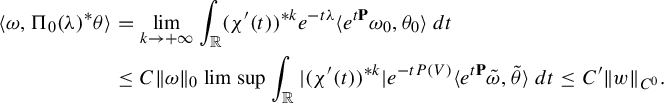 $$ \begin{align*} \langle\omega, \Pi_0(\unicode{x3bb})^{*}\theta\rangle& =\lim_{k\to+\infty}\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega_0, \theta_0\rangle\,dt \\ &\leq C\|\omega\|_0\limsup\int_{\mathbb R}|(\chi'(t))^{*k}|e^{-tP(V)}\langle e^{t\mathbf P}\tilde \omega, \tilde \theta\rangle\,dt \leq C'\|w\|_{C^0}. \end{align*} $$
$$ \begin{align*} \langle\omega, \Pi_0(\unicode{x3bb})^{*}\theta\rangle& =\lim_{k\to+\infty}\int_{\mathbb R}(\chi'(t))^{*k}e^{-t\unicode{x3bb}}\langle e^{t\mathbf P}\omega_0, \theta_0\rangle\,dt \\ &\leq C\|\omega\|_0\limsup\int_{\mathbb R}|(\chi'(t))^{*k}|e^{-tP(V)}\langle e^{t\mathbf P}\tilde \omega, \tilde \theta\rangle\,dt \leq C'\|w\|_{C^0}. \end{align*} $$
The above bound actually holds for any
![]() $\theta $
and
$\theta $
and
![]() $\omega $
, and we get that every co-resonant state is an order zero current.
$\omega $
, and we get that every co-resonant state is an order zero current.
Restrictions of co-resonant state on unstable manifolds are well defined. Following the strategy of the proof of Proposition 3.2, we consider a co-resonant state
![]() $\theta $
which satisfies
$\theta $
which satisfies
![]() $\mathrm {WF}(\theta )\subset E_s^{*}$
. For any
$\mathrm {WF}(\theta )\subset E_s^{*}$
. For any
![]() $x\in \mathcal M$
, we can thus define the restriction of
$x\in \mathcal M$
, we can thus define the restriction of
![]() $\theta $
to
$\theta $
to
![]() $\mathcal W^u(x)$
. We will denote
$\mathcal W^u(x)$
. We will denote
![]() $\theta _x:=\theta _{|\mathcal W^u(x)}$
. More explicitly, for a smooth function
$\theta _x:=\theta _{|\mathcal W^u(x)}$
. More explicitly, for a smooth function
![]() $f\in C^{\infty }(\mathcal M)$
, we can define
$f\in C^{\infty }(\mathcal M)$
, we can define
where the bracket denotes the distributional pairing and
![]() $[\mathcal W^u(x)]$
denotes the
$[\mathcal W^u(x)]$
denotes the
![]() $d_u$
-current which consists in integrating over the unstable manifold
$d_u$
-current which consists in integrating over the unstable manifold
![]() $\mathcal W^u(x)$
. Then,
$\mathcal W^u(x)$
. Then,
![]() $\theta _x$
is seen to be of order zero, in other words,
$\theta _x$
is seen to be of order zero, in other words,
![]() $\{\theta _x\mid x\in \mathcal M\}$
defines a system of measures on the unstable leaves.
$\{\theta _x\mid x\in \mathcal M\}$
defines a system of measures on the unstable leaves.
The system of measures
![]() $\{\theta _x\mid x\in \mathcal M\}$
satisfies
$\{\theta _x\mid x\in \mathcal M\}$
satisfies
![]() $\varphi _t$
-conformality. This is again a consequence of the fact that
$\varphi _t$
-conformality. This is again a consequence of the fact that
![]() $\theta $
is a co-resonant state. More precisely, for any smooth function
$\theta $
is a co-resonant state. More precisely, for any smooth function
![]() $f\in C^{\infty }(\mathcal M)$
, we can write
$f\in C^{\infty }(\mathcal M)$
, we can write
Using
![]() $e^{t\mathbf P}( f[\mathcal W^u(x)])=e^{t\mathbf P} f[\mathcal W^u(\varphi _t x)]$
then yields
$e^{t\mathbf P}( f[\mathcal W^u(x)])=e^{t\mathbf P} f[\mathcal W^u(\varphi _t x)]$
then yields
which is exactly the
![]() $\varphi _t$
-conformality for the potential V.
$\varphi _t$
-conformality for the potential V.
The system of measures
![]() $\{\theta _x \mid x\in \mathcal M\}$
satisfies the change of variable by holonomy. This a consequence of the continuity of
$\{\theta _x \mid x\in \mathcal M\}$
satisfies the change of variable by holonomy. This a consequence of the continuity of
![]() $x\mapsto \theta _x$
, which is shown as in the proof of Proposition 3.2. Indeed, another way of obtaining
$x\mapsto \theta _x$
, which is shown as in the proof of Proposition 3.2. Indeed, another way of obtaining
![]() $\theta _x$
is to write
$\theta _x$
is to write
![]() $\theta $
as a linear combination of smooth
$\theta $
as a linear combination of smooth
![]() $d_u$
-form with distributional coefficients in
$d_u$
-form with distributional coefficients in
![]() $\mathcal H^{-s}$
. Then, the restriction
$\mathcal H^{-s}$
. Then, the restriction
![]() $\theta _x$
is obtained by pulling back the smooth forms and the coefficients. The pullback on the coefficients are well defined by the wavefront set condition and we deduce the continuity property by the continuity of the coefficients.
$\theta _x$
is obtained by pulling back the smooth forms and the coefficients. The pullback on the coefficients are well defined by the wavefront set condition and we deduce the continuity property by the continuity of the coefficients.
Following the proof of Proposition 3.2 and using [Reference Climenhaga10, Corollary 3.12], we obtain the existence of a constant
![]() $c>0$
such that for any
$c>0$
such that for any
![]() $x\in \mathcal M$
, one has
$x\in \mathcal M$
, one has
![]() $\theta _x=c m^u_{x,V}$
.
$\theta _x=c m^u_{x,V}$
.
The first resonance
![]() $P(V)$
is simple. The first part of the proof shows that it suffices to prove that for any
$P(V)$
is simple. The first part of the proof shows that it suffices to prove that for any
![]() $\omega \in C^{\alpha }(\mathcal M; \Lambda _0^{d_s})$
, one has
$\omega \in C^{\alpha }(\mathcal M; \Lambda _0^{d_s})$
, one has
![]() $(\omega , \theta )=c(\omega , m^u_V)$
. Note that such a
$(\omega , \theta )=c(\omega , m^u_V)$
. Note that such a
![]() $\omega $
writes
$\omega $
writes
![]() $\omega =f\mathrm {vol}_{\mathcal W^u(x)}$
for some
$\omega =f\mathrm {vol}_{\mathcal W^u(x)}$
for some
![]() $f\in C^{0}(\mathcal M)$
, we can then write
$f\in C^{0}(\mathcal M)$
, we can then write
where
![]() $\delta _{\mathcal W^u(x)}$
is the integration of function on the unstable manifold of x (see equation (56)). Remark that here, the last bracket is the usual distributional pairing. In particular,
$\delta _{\mathcal W^u(x)}$
is the integration of function on the unstable manifold of x (see equation (56)). Remark that here, the last bracket is the usual distributional pairing. In particular,
![]() $\theta _x$
is the restriction to the unstable manifold
$\theta _x$
is the restriction to the unstable manifold
![]() $\mathcal W^u(x)$
of the measure
$\mathcal W^u(x)$
of the measure
![]() ${\mathrm {vol}_{\mathcal W^u}\wedge \alpha \wedge \theta }$
. Using the last part of the proof of Proposition 3.2 then yields that
${\mathrm {vol}_{\mathcal W^u}\wedge \alpha \wedge \theta }$
. Using the last part of the proof of Proposition 3.2 then yields that
This concludes the proof.
We can now prove the second part of Theorem 1.2 for
![]() $d_s$
-forms.
$d_s$
-forms.
Proposition 4.4. The equilibrium state
![]() $\mu _{V}$
is given by the averaging formula (8).
$\mu _{V}$
is given by the averaging formula (8).
Finally, if the flow is weak mixing with respect to the equilibrium state
![]() $\mu _{V}$
, then the only resonance on the critical axis is
$\mu _{V}$
, then the only resonance on the critical axis is
![]() $P(V)$
.
$P(V)$
.
Proof. The averaging formula is derived from the product formula of Lemma 4.1 and the expression of the projector
![]() $ \Pi _0(P(V))$
using the exact same argument as in the proof of Proposition 3.3. Suppose now that there is another co-resonant state
$ \Pi _0(P(V))$
using the exact same argument as in the proof of Proposition 3.3. Suppose now that there is another co-resonant state
![]() $\theta $
associated to a resonance
$\theta $
associated to a resonance
![]() $P(V)+i\unicode{x3bb} $
on the critical axis. We use the fact that
$P(V)+i\unicode{x3bb} $
on the critical axis. We use the fact that
![]() $\theta $
is of order
$\theta $
is of order
![]() $0$
as well as [Reference Simon35, Ch. 6, equation (2.6)] to get that there exists a Borel measure
$0$
as well as [Reference Simon35, Ch. 6, equation (2.6)] to get that there exists a Borel measure
![]() $\mu _{\theta }$
and a
$\mu _{\theta }$
and a
![]() $\mu _{\theta }^\unicode{x3bb} $
-measurable function
$\mu _{\theta }^\unicode{x3bb} $
-measurable function
![]() $T_{\theta }$
with values in
$T_{\theta }$
with values in
![]() $\Lambda ^{d_s}(E_u^{*}\oplus E_s^{*})$
normalized
$\Lambda ^{d_s}(E_u^{*}\oplus E_s^{*})$
normalized
![]() $\mu _{\theta }^\unicode{x3bb} $
-almost everywhere such that
$\mu _{\theta }^\unicode{x3bb} $
-almost everywhere such that
where the bracket here denotes the scalar product on
![]() $\Lambda ^{d_s}(E_u^{*}\oplus E_s^{*})$
. Moreover, the measure
$\Lambda ^{d_s}(E_u^{*}\oplus E_s^{*})$
. Moreover, the measure
![]() $\mu _{\theta }^\unicode{x3bb} $
is defined by
$\mu _{\theta }^\unicode{x3bb} $
is defined by
The proof of the previous proposition showed that there is a
![]() $C>0$
such that
$C>0$
such that
Now, using equations (62), (68), as well as the bound
(which can be found in the proof of [Reference Climenhaga10, Theorem 3.10]), we get that
![]() $\mu $
satisfies an upper Gibbs bound. In other words, we have
$\mu $
satisfies an upper Gibbs bound. In other words, we have
![]() $\mu \ll \mu _V$
. In particular, the Radon–Nikodym density
$\mu \ll \mu _V$
. In particular, the Radon–Nikodym density
![]() $h:={d\mu _\theta ^\unicode{x3bb} }/{d\mu }$
is an element of
$h:={d\mu _\theta ^\unicode{x3bb} }/{d\mu }$
is an element of
![]() $L^{\infty }(\mathcal M, \mu _V)$
.
$L^{\infty }(\mathcal M, \mu _V)$
.
We use [Reference Reed and Simon33, Theorem VII.14] to see that the flow is weakly mixing if and only if the only eigenvalue is
![]() $1$
and it is a simple eigenvalue. In other words, if
$1$
and it is a simple eigenvalue. In other words, if
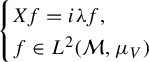 $$ \begin{align} \begin{cases} Xf=i\unicode{x3bb} f,\\ f\in L^2(\mathcal M,\mu_{V}) \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} Xf=i\unicode{x3bb} f,\\ f\in L^2(\mathcal M,\mu_{V}) \end{cases} \end{align} $$
has no solution except for
![]() $\unicode{x3bb} =0$
and f constant. However, then, we have shown that h is a non-trivial solution of the above system which contradicts weak mixing.
$\unicode{x3bb} =0$
and f constant. However, then, we have shown that h is a non-trivial solution of the above system which contradicts weak mixing.
5 Other critical axes and regularity of the pressure
In this section, we will prove the statement about critical axes of Theorem 1.1 as well as Corollary 1.1.
Proof. We start from the Guillemin trace formula,
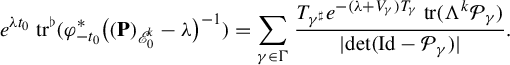 $$ \begin{align*}e^{\unicode{x3bb} t_0}\operatorname{\mathrm{tr}}^{\flat} (\varphi_{-t_0}^{*}\big( (\mathbf{P})_{\mathscr E_0^{k}}-\unicode{x3bb}\big)^{-1})=\sum_{\gamma\in \Gamma}\frac{T_{\gamma^{\sharp}}e^{-(\unicode{x3bb}+V_{\gamma}) T_{\gamma}}\operatorname{\mathrm{tr}}(\Lambda^{k}\mathcal P_{\gamma})}{|\kern-2.2pt\det(\mathrm{Id}-\mathcal P_{\gamma})|}.\end{align*} $$
$$ \begin{align*}e^{\unicode{x3bb} t_0}\operatorname{\mathrm{tr}}^{\flat} (\varphi_{-t_0}^{*}\big( (\mathbf{P})_{\mathscr E_0^{k}}-\unicode{x3bb}\big)^{-1})=\sum_{\gamma\in \Gamma}\frac{T_{\gamma^{\sharp}}e^{-(\unicode{x3bb}+V_{\gamma}) T_{\gamma}}\operatorname{\mathrm{tr}}(\Lambda^{k}\mathcal P_{\gamma})}{|\kern-2.2pt\det(\mathrm{Id}-\mathcal P_{\gamma})|}.\end{align*} $$
We know by Lemma 4.2 that the critical axis of
![]() $(\mathbf {P})_{\mathscr E_0^{d_s}}$
is
$(\mathbf {P})_{\mathscr E_0^{d_s}}$
is
![]() $\{\mathrm {Re}(\unicode{x3bb} )=P(V)\}$
. We will prove that the other functions are analytic in a half-plane
$\{\mathrm {Re}(\unicode{x3bb} )=P(V)\}$
. We will prove that the other functions are analytic in a half-plane
![]() $\{\mathrm {Re}(\unicode{x3bb} )>P(V)-\epsilon \}$
for some
$\{\mathrm {Re}(\unicode{x3bb} )>P(V)-\epsilon \}$
for some
![]() $\epsilon>0.$
We list the eigenvalues of the Poincaré map
$\epsilon>0.$
We list the eigenvalues of the Poincaré map
for some uniform constant
![]() $\eta>0$
given by the Anosov property. Now we can compute
$\eta>0$
given by the Anosov property. Now we can compute
where
![]() $\sigma _k$
is the kth symmetric polynomial. We see that the maximum value of
$\sigma _k$
is the kth symmetric polynomial. We see that the maximum value of
![]() $\operatorname {\mathrm {tr}}(\Lambda ^{k}\mathcal P_{\gamma })$
is attained at
$\operatorname {\mathrm {tr}}(\Lambda ^{k}\mathcal P_{\gamma })$
is attained at
![]() $k=d_s$
, where one can choose all eigenvalues larger than
$k=d_s$
, where one can choose all eigenvalues larger than
![]() $1$
without choosing any other eigenvalues. In particular, there is a constant
$1$
without choosing any other eigenvalues. In particular, there is a constant
![]() $C>0$
, independent of
$C>0$
, independent of
![]() $\gamma $
and k such that if
$\gamma $
and k such that if
![]() $k\neq d_s$
, then
$k\neq d_s$
, then
However now, we know that for
![]() $k=d_s$
, the trace is analytic and converges in
$k=d_s$
, the trace is analytic and converges in
![]() $\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
. In particular, because all terms are positive, if
$\{\mathrm {Re}(\unicode{x3bb} )>P(V)\}$
. In particular, because all terms are positive, if
![]() $\epsilon <\eta $
, then for any
$\epsilon <\eta $
, then for any
![]() $\unicode{x3bb} \in (P(V)-\epsilon , P(V))$
, one has
$\unicode{x3bb} \in (P(V)-\epsilon , P(V))$
, one has
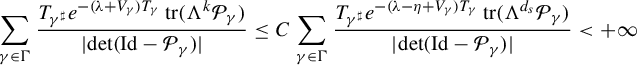 $$ \begin{align*} \sum_{\gamma\in \Gamma}\frac{T_{\gamma^{\sharp}}e^{-(\unicode{x3bb}+V_{\gamma}) T_{\gamma}}\operatorname{\mathrm{tr}}(\Lambda^{k}\mathcal P_{\gamma})}{|\kern-2.1pt\det(\mathrm{Id}-\mathcal P_{\gamma})|}\leq C\sum_{\gamma\in \Gamma}\frac{T_{\gamma^{\sharp}}e^{-(\unicode{x3bb}-\eta +V_{\gamma}) T_{\gamma}}\operatorname{\mathrm{tr}}(\Lambda^{d_s}\mathcal P_{\gamma})}{|\kern-2.1pt\det(\mathrm{Id}-{\mathcal P}_{\gamma})|}<+\infty \end{align*} $$
$$ \begin{align*} \sum_{\gamma\in \Gamma}\frac{T_{\gamma^{\sharp}}e^{-(\unicode{x3bb}+V_{\gamma}) T_{\gamma}}\operatorname{\mathrm{tr}}(\Lambda^{k}\mathcal P_{\gamma})}{|\kern-2.1pt\det(\mathrm{Id}-\mathcal P_{\gamma})|}\leq C\sum_{\gamma\in \Gamma}\frac{T_{\gamma^{\sharp}}e^{-(\unicode{x3bb}-\eta +V_{\gamma}) T_{\gamma}}\operatorname{\mathrm{tr}}(\Lambda^{d_s}\mathcal P_{\gamma})}{|\kern-2.1pt\det(\mathrm{Id}-{\mathcal P}_{\gamma})|}<+\infty \end{align*} $$
and this shows that the left-hand side is analytic in the region
![]() $\{\mathrm {Re}(\unicode{x3bb} )>P(V)-\epsilon \}$
as claimed.
$\{\mathrm {Re}(\unicode{x3bb} )>P(V)-\epsilon \}$
as claimed.
Now we prove Corollary 1.1.
Proof. From [Reference Bonthonneau3, Theorem 1], we can find a
![]() $C^1$
neighborhood
$C^1$
neighborhood
![]() $\mathcal U$
of
$\mathcal U$
of
![]() $(X_0, V_0)$
and an anisotropic Sobolev space
$(X_0, V_0)$
and an anisotropic Sobolev space
![]() $\mathcal H^{s_0}$
such that for any
$\mathcal H^{s_0}$
such that for any
![]() $(X,V)\in \mathcal U$
, the operator
$(X,V)\in \mathcal U$
, the operator
![]() $-X+V$
has discrete spectrum in
$-X+V$
has discrete spectrum in
![]() $\{\mathrm {Re}(\unicode{x3bb} )\geq -1\}$
. Now, the pressure
$\{\mathrm {Re}(\unicode{x3bb} )\geq -1\}$
. Now, the pressure
![]() $P_X(V+J^u)$
is obtained as a simple eigenvalue (from Theorem 1.1) of a smooth family of operators acting on
$P_X(V+J^u)$
is obtained as a simple eigenvalue (from Theorem 1.1) of a smooth family of operators acting on
![]() $\mathcal H^{s_0}$
. One deduces the regularity statement by a perturbation argument of the resolvent, just like in the proof of [Reference Bonthonneau3, Corollary 2]. The regularity of
$\mathcal H^{s_0}$
. One deduces the regularity statement by a perturbation argument of the resolvent, just like in the proof of [Reference Bonthonneau3, Corollary 2]. The regularity of
![]() $P_X(V)$
is obtained by the same argument but on
$P_X(V)$
is obtained by the same argument but on
![]() $d_s$
-forms.
$d_s$
-forms.
Acknowledgements
The author would like to thank Colin Guillarmou and Thibault Lefeuvre for introducing him to to this problem and more generally to the field, as well as for their careful and precious guidance during the writing of this paper. The author would also like to thank Gabriel Paternain and Gabriel Rivière for making some comments on an earlier version of the paper, and Julien Moy for assistance with making Figure 1.
A Appendix. Hölder continuity of a distributional product
In this appendix, we fix a continuous function
![]() $\varphi $
and an order zero distribution
$\varphi $
and an order zero distribution
![]() $\theta $
such that
$\theta $
such that
![]() $\mathrm {WF}(\theta )\subset E_s^{*}$
. This means that the distributional product
$\mathrm {WF}(\theta )\subset E_s^{*}$
. This means that the distributional product
![]() $(\delta _{\mathcal W^u(x)},\varphi \theta )$
is well defined. We will prove the following result.
$(\delta _{\mathcal W^u(x)},\varphi \theta )$
is well defined. We will prove the following result.
Proposition A.1. There exists
![]() $C(\varphi )>0,\alpha >0$
and
$C(\varphi )>0,\alpha >0$
and
![]() $\epsilon>0$
such that if
$\epsilon>0$
such that if
![]() $d(x,x')<\epsilon $
, then
$d(x,x')<\epsilon $
, then
Here, the exponent
![]() $\alpha $
only depends on the unstable foliation.
$\alpha $
only depends on the unstable foliation.
Proof. The proof is mostly contained in the proof of [Reference Weich38, Proposition 6]. Indeed, to get equation (A.1), one needs to prove superpolynomial decay of the Fourier transform of
![]() $\delta _{\mathcal W^u(x)}-\delta _{\mathcal W^u(x')}$
for
$\delta _{\mathcal W^u(x)}-\delta _{\mathcal W^u(x')}$
for
![]() $\xi \notin \Omega $
, where a small conic neighborhood of
$\xi \notin \Omega $
, where a small conic neighborhood of
![]() $E_0^{*}\oplus E_u^{*}$
with a constant that is Hölder continuous. In other words,
$E_0^{*}\oplus E_u^{*}$
with a constant that is Hölder continuous. In other words,
where the Fourier transforms should be, strictly speaking, defined locally using charts. The super polynomial decay is proved in [Reference Weich38, Proposition 6] using integration by parts. Inspection of the proof shows that all
![]() $C^k$
norms of the operator
$C^k$
norms of the operator
![]() $L_l$
, which is used to integrate by parts, depend Hölder continuously on the base point x. Weich only uses continuity in the proof to get uniform constant
$L_l$
, which is used to integrate by parts, depend Hölder continuously on the base point x. Weich only uses continuity in the proof to get uniform constant
![]() $C_N$
, but using the Hölder continuity instead to bound the difference yields the refinement above.
$C_N$
, but using the Hölder continuity instead to bound the difference yields the refinement above.
On
![]() $\Omega $
, we use the fact that the Fourier transform of
$\Omega $
, we use the fact that the Fourier transform of
![]() $\theta $
decays super polynomially and that
$\theta $
decays super polynomially and that
![]() $|\widehat {\delta _{\mathcal W^u(x)}}(\xi )-\widehat {\delta _{\mathcal W^u(x')}}(\xi )|$
has order zero. Actually, using the Hölder continuity of the foliation, the above difference is again controlled by
$|\widehat {\delta _{\mathcal W^u(x)}}(\xi )-\widehat {\delta _{\mathcal W^u(x')}}(\xi )|$
has order zero. Actually, using the Hölder continuity of the foliation, the above difference is again controlled by
![]() $d(x,x')^{\alpha }$
and using the definition of the distributional product yields equation (A.1).
$d(x,x')^{\alpha }$
and using the definition of the distributional product yields equation (A.1).








