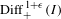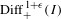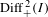Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brum, Joaquín
Matte Bon, Nicolás
Rivas, Cristóbal
and
Triestino, Michele
2024.
Solvable groups and affine actions on the line.
Journal de l’École polytechnique — Mathématiques,
Vol. 12,
Issue. ,
p.
23.
Carnevale, João
2025.
Groups acting on the line with at most 2 fixed points: an extension of Solodov’s theorem.
Comptes Rendus. Mathématique,
Vol. 363,
Issue. G10,
p.
951.