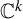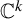Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bianchi, Fabrizio
and
Dinh, Tien-Cuong
2024.
Every complex Hénon map is exponentially mixing of all orders and satisfies the CLT.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,