No CrossRef data available.
Article contents
Existence and non-existence of solutions to the coboundary equation for measure-preserving systems
Published online by Cambridge University Press: 04 July 2022
Abstract
A fundamental question in the field of cohomology of dynamical systems is to determine when there are solutions to the coboundary equation: $$ \begin{align*} f = g - g \circ T. \end{align*} $$
$$ \begin{align*} f = g - g \circ T. \end{align*} $$
In many cases, T is given to be an ergodic invertible measure-preserving transformation on a standard probability space 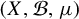 $(X, {\mathcal B}, \mu )$ and
$(X, {\mathcal B}, \mu )$ and 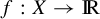 is contained in
is contained in 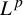 $L^p$ for
$L^p$ for 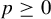 $p \geq 0$. We extend previous results by showing for any measurable f that is non-zero on a set of positive measure, the class of measure-preserving T with a measurable solution g is meager (including the case where
$p \geq 0$. We extend previous results by showing for any measurable f that is non-zero on a set of positive measure, the class of measure-preserving T with a measurable solution g is meager (including the case where 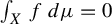 $\int _X f\,d\mu = 0$). From this fact, a natural question arises: given f, does there always exist a solution pair T and g? In regards to this question, our main results are as follows. Given measurable f, there exist an ergodic invertible measure-preserving transformation T and measurable function g such that
$\int _X f\,d\mu = 0$). From this fact, a natural question arises: given f, does there always exist a solution pair T and g? In regards to this question, our main results are as follows. Given measurable f, there exist an ergodic invertible measure-preserving transformation T and measurable function g such that 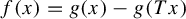 $f(x) = g(x) - g(Tx)$ for almost every (a.e.)
$f(x) = g(x) - g(Tx)$ for almost every (a.e.) 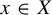 $x\in X$, if and only if
$x\in X$, if and only if 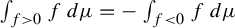 $\int _{f> 0} f\,d\mu = - \int _{f < 0} f\,d\mu $ (whether finite or
$\int _{f> 0} f\,d\mu = - \int _{f < 0} f\,d\mu $ (whether finite or 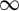 $\infty $). Given mean-zero
$\infty $). Given mean-zero 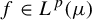 $f \in L^p(\mu )$ for
$f \in L^p(\mu )$ for 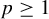 $p \geq 1$, there exist an ergodic invertible measure-preserving T and
$p \geq 1$, there exist an ergodic invertible measure-preserving T and 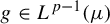 $g \in L^{p-1}(\mu )$ such that
$g \in L^{p-1}(\mu )$ such that 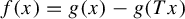 $f(x) = g(x) - g( Tx )$ for a.e.
$f(x) = g(x) - g( Tx )$ for a.e. 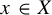 $x \in X$. In some sense, the previous existence result is the best possible. For
$x \in X$. In some sense, the previous existence result is the best possible. For 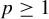 $p \geq 1$, there exists a dense
$p \geq 1$, there exists a dense 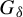 $G_{\delta }$ set of mean-zero
$G_{\delta }$ set of mean-zero 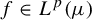 $f \in L^p(\mu )$ such that for any ergodic invertible measure-preserving T and any measurable g such that
$f \in L^p(\mu )$ such that for any ergodic invertible measure-preserving T and any measurable g such that 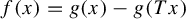 $f(x) = g(x) - g(Tx)$ almost everywhere, then
$f(x) = g(x) - g(Tx)$ almost everywhere, then 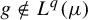 $g \notin L^q(\mu )$ for
$g \notin L^q(\mu )$ for 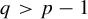 $q> p - 1$. Finally, it is shown that we cannot expect finite moments for solutions g, when
$q> p - 1$. Finally, it is shown that we cannot expect finite moments for solutions g, when 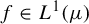 $f \in L^1(\mu )$. In particular, given any
$f \in L^1(\mu )$. In particular, given any 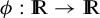 such that
such that 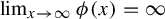 $\lim _{x\to \infty } \phi (x) = \infty $, there exist mean-zero
$\lim _{x\to \infty } \phi (x) = \infty $, there exist mean-zero 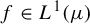 $f \in L^1(\mu )$ such that for any solutions T and g, the transfer function g satisfies:
$f \in L^1(\mu )$ such that for any solutions T and g, the transfer function g satisfies: 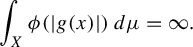 $$ \begin{align*} \int_{X} \phi ( | g(x) | )\,d\mu = \infty. \end{align*} $$
$$ \begin{align*} \int_{X} \phi ( | g(x) | )\,d\mu = \infty. \end{align*} $$
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press


