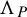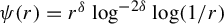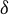1. Introduction
Iterated function systems (IFSs) have been studied intensively since the 1980s by several groups of researchers, including Bandt, Barnsley, Dekking, Falconer, Graf, Hata, Hutchinson, Mauldin, Schief, Simon, Solomyak, and Urbański. For a very selective sampling of such research see [Reference Bandt and Graf2–Reference Barnsley4, Reference Dekking9, Reference Falconer12, Reference Graf, Mauldin and Williams13, Reference Hutchinson20, Reference Mauldin and Urbański24, Reference Mauldin and Urbański26, Reference Schief33, Reference Simon, Solomyak and Urbański35]. Much of the early research on IFSs focused on systems with a finite number of Euclidean similarities as generators. Since the 1990s the theory has been extended to handle systems with countably many conformal maps. Mauldin and Urbański were among the pioneers of this extension of IFS theory, first to the study of infinite conformal iterated function systems (CIFSs), and then to their generalizations, namely, conformal graph directed Markov systems (CGDMSs) that may be used to study Fuchsian and Kleinian group limit sets as well as Julia sets associated with holomorphic and meromorphic iteration; see [Reference Mauldin and Urbański24, Reference Mauldin and Urbański26].
In particular, the CIFS/CGDMS framework may be leveraged to encode a variety of sets that appear naturally at the interfaces of dynamical systems, fractal geometry and Diophantine approximation. In particular, with an eye on the focus of our paper, one can encode real numbers via their continued fraction expansions leading to the Gauss continued fraction IFS, which is a prime example of an infinite CIFS whose generators are the Möbius maps
![]() $x \mapsto 1/(a + x)$
for
$x \mapsto 1/(a + x)$
for
![]() $a \in {\mathbb {N}}$
. Given any subset
$a \in {\mathbb {N}}$
. Given any subset
![]() $A\subset {\mathbb {N}}$
, let
$A\subset {\mathbb {N}}$
, let
![]() $\Lambda _A$
denote the set of all irrationals
$\Lambda _A$
denote the set of all irrationals
![]() $x\in [0,1]$
whose continued fraction partial quotients all lie in A. Then
$x\in [0,1]$
whose continued fraction partial quotients all lie in A. Then
![]() $\Lambda _A$
may be expressed as the limit set of the subsystem of the Gauss IFS that comprises the maps
$\Lambda _A$
may be expressed as the limit set of the subsystem of the Gauss IFS that comprises the maps
![]() $x \mapsto 1/(a + x)$
for
$x \mapsto 1/(a + x)$
for
![]() $a \in A$
; see, for example, [Reference Chousionis, Leykekhman and Urbański7, Reference Hensley18, Reference Mauldin and Urbański25].
$a \in A$
; see, for example, [Reference Chousionis, Leykekhman and Urbański7, Reference Hensley18, Reference Mauldin and Urbański25].
We focus on
![]() $\Lambda _P$
, the prime Cantor set of our title, that is, the Cantor set of irrationals whose continued fraction entries are prime numbers. Let
$\Lambda _P$
, the prime Cantor set of our title, that is, the Cantor set of irrationals whose continued fraction entries are prime numbers. Let
![]() $\delta = \delta _P$
denote the common value [Reference Mauldin and Urbański25, Theorems 2.7 and 2.11] for the Hausdorff and packing dimensions of
$\delta = \delta _P$
denote the common value [Reference Mauldin and Urbański25, Theorems 2.7 and 2.11] for the Hausdorff and packing dimensions of
![]() $\Lambda _P$
. Using a result due to Erdős [Reference Erdös10] guaranteeing the existence of arbitrarily large two-sided gaps in the sequence of primes, Mauldin and Urbański [Reference Mauldin and Urbański25, Corollaries 4.5 and 5.6] proved that despite there being a conformal measure and a corresponding invariant Borel probability measure for this CIFS, the
$\Lambda _P$
. Using a result due to Erdős [Reference Erdös10] guaranteeing the existence of arbitrarily large two-sided gaps in the sequence of primes, Mauldin and Urbański [Reference Mauldin and Urbański25, Corollaries 4.5 and 5.6] proved that despite there being a conformal measure and a corresponding invariant Borel probability measure for this CIFS, the
![]() $\delta $
-dimensional Hausdorff and packing measures were zero and infinity, respectively. (Such phenomena cannot occur in the setting of finite-alphabet Gauss IFSs, since their limit sets are Ahlfors regular.) This result led naturally to the surprisingly resistant problem, first stated by Mauldin and Urbański in [Reference Mauldin and Urbański25, Problem 2 in §7] and later repeated by Mauldin in the 2013 Erdős centennial volume [Reference Mauldin23, Problem 7.1], of determining whether there was an appropriate dimension function with respect to which the Hausdorff and packing measures of
$\delta $
-dimensional Hausdorff and packing measures were zero and infinity, respectively. (Such phenomena cannot occur in the setting of finite-alphabet Gauss IFSs, since their limit sets are Ahlfors regular.) This result led naturally to the surprisingly resistant problem, first stated by Mauldin and Urbański in [Reference Mauldin and Urbański25, Problem 2 in §7] and later repeated by Mauldin in the 2013 Erdős centennial volume [Reference Mauldin23, Problem 7.1], of determining whether there was an appropriate dimension function with respect to which the Hausdorff and packing measures of
![]() $\Lambda _P$
were positive and finite. The study of such dimension functions, called exact dimension functions, has offered mathematicians myriad challenges over the past century. A very selective sampling of results follows: for Liouville numbers see [Reference Olsen and Renfro27]; for Bedford–McMullen self-affine carpets see [Reference Peres28, Reference Peres29]; for geometrically finite Kleinian limit sets see [Reference Simmons34]; and for random recursive constructions, Brownian sample paths and beyond see [Reference Graf, Mauldin and Williams13, Reference Taylor38].
$\Lambda _P$
were positive and finite. The study of such dimension functions, called exact dimension functions, has offered mathematicians myriad challenges over the past century. A very selective sampling of results follows: for Liouville numbers see [Reference Olsen and Renfro27]; for Bedford–McMullen self-affine carpets see [Reference Peres28, Reference Peres29]; for geometrically finite Kleinian limit sets see [Reference Simmons34]; and for random recursive constructions, Brownian sample paths and beyond see [Reference Graf, Mauldin and Williams13, Reference Taylor38].
2. Main theorems
We start by stating our main results; precise definitions will follow in the next section. Let
![]() $\delta = \delta _P$
denote the common value [Reference Mauldin and Urbański25, Theorems 2.7 and 2.11] for the Hausdorff and packing dimensions of
$\delta = \delta _P$
denote the common value [Reference Mauldin and Urbański25, Theorems 2.7 and 2.11] for the Hausdorff and packing dimensions of
![]() $\Lambda _P$
. If
$\Lambda _P$
. If
![]() $\mu $
is a locally finite Borel measure on
$\mu $
is a locally finite Borel measure on
![]() $\mathbb R$
, then we let
$\mathbb R$
, then we let
 $$ \begin{align*} \mathcal H^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal H^\psi(A): \mu(\mathbb R\setminus A) = 0\},\\ \mathcal P^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal P^\psi(A): \mu(\mathbb R\setminus A) = 0\}. \end{align*} $$
$$ \begin{align*} \mathcal H^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal H^\psi(A): \mu(\mathbb R\setminus A) = 0\},\\ \mathcal P^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal P^\psi(A): \mu(\mathbb R\setminus A) = 0\}. \end{align*} $$
A function
![]() $\psi $
is doubling if for all
$\psi $
is doubling if for all
![]() $C_1 \geq 1$
, there exists
$C_1 \geq 1$
, there exists
![]() $C_2 \geq 1$
such that for all
$C_2 \geq 1$
such that for all
![]() $x,y$
with
$x,y$
with
![]() $C_1^{-1} \leq x/y \leq C_1$
, we have
$C_1^{-1} \leq x/y \leq C_1$
, we have
![]() $C_2^{-1} \leq \psi (x)/\psi (y) \leq C_2$
.
$C_2^{-1} \leq \psi (x)/\psi (y) \leq C_2$
.
Theorem 2.1. Let
![]() $\mu = \mu _P$
be the conformal measure on
$\mu = \mu _P$
be the conformal measure on
![]() $\Lambda _P$
, and let
$\Lambda _P$
, and let
![]() $\psi $
be a doubling dimension function such that
$\psi $
be a doubling dimension function such that
![]() $\Psi (r) = r^{-\delta } \psi (r)$
is monotonic. Then
$\Psi (r) = r^{-\delta } \psi (r)$
is monotonic. Then
![]() $\mathcal H^\psi (\mu ) = 0$
if the series
$\mathcal H^\psi (\mu ) = 0$
if the series
 $$ \begin{align} \sum_{k=1}^\infty \frac{y^{({1-2\delta})/({1-\delta})}}{(\log y)^{{\delta}/({1-\delta})}}\upharpoonleft_{y=\Psi(\unicode{x3bb}^{-k})} \end{align} $$
$$ \begin{align} \sum_{k=1}^\infty \frac{y^{({1-2\delta})/({1-\delta})}}{(\log y)^{{\delta}/({1-\delta})}}\upharpoonleft_{y=\Psi(\unicode{x3bb}^{-k})} \end{align} $$
diverges, and
![]() $=\infty $
if it converges, for all (equivalently, for any) fixed
$=\infty $
if it converges, for all (equivalently, for any) fixed
![]() $\unicode{x3bb}> 1$
.
$\unicode{x3bb}> 1$
.
Note that
![]() $1/2 < \delta \approx 0.657 < 1$
[Reference Chousionis, Leykekhman and Urbański7, Table 1 and §3], so the exponent in the numerator is negative.
$1/2 < \delta \approx 0.657 < 1$
[Reference Chousionis, Leykekhman and Urbański7, Table 1 and §3], so the exponent in the numerator is negative.
The following corollary negatively resolves [Reference Mauldin23, Problem 7.1] and part of [Reference Mauldin and Urbański25, Problem 2 in §7] for sufficiently regular dimension functions, for example Hardy L-functions [Reference Hardy16, Reference Hardy17].
Corollary 2.2. For any doubling dimension function
![]() $\psi $
such that
$\psi $
such that
![]() $\Psi (r) = r^{-\delta } \psi (r)$
is monotonic, we have
$\Psi (r) = r^{-\delta } \psi (r)$
is monotonic, we have
![]() $\mathcal H^\psi (\Lambda _P) \in \{0,\infty \}$
.
$\mathcal H^\psi (\Lambda _P) \in \{0,\infty \}$
.
Proof. By way of contradiction suppose that
![]() $0 < \mathcal H^\psi (\Lambda _P) < \infty $
. Then
$0 < \mathcal H^\psi (\Lambda _P) < \infty $
. Then
![]() $\mathcal H^\psi \upharpoonleft \Lambda _P$
is a conformal measure on
$\mathcal H^\psi \upharpoonleft \Lambda _P$
is a conformal measure on
![]() $\Lambda _P$
and therefore a scalar multiple of
$\Lambda _P$
and therefore a scalar multiple of
![]() $\mu _P$
, and thus
$\mu _P$
, and thus
![]() $\mathcal H^\psi (\Lambda _P) = \mathcal H^\psi (\mathcal H^\psi \upharpoonleft \Lambda _P) \in \{0,\infty \}$
by Theorem 2.1, a contradiction.
$\mathcal H^\psi (\Lambda _P) = \mathcal H^\psi (\mathcal H^\psi \upharpoonleft \Lambda _P) \in \{0,\infty \}$
by Theorem 2.1, a contradiction.
Remark. Letting
![]() $\psi (r) = r^\delta \log ^s(1/r)$
with
$\psi (r) = r^\delta \log ^s(1/r)$
with
![]() $s> ({1-\delta })/({2\delta -1})$
gives an example of a function that satisfies the hypotheses of Theorem 2.1 such that the series (2.1) converges. For this function, we have
$s> ({1-\delta })/({2\delta -1})$
gives an example of a function that satisfies the hypotheses of Theorem 2.1 such that the series (2.1) converges. For this function, we have
![]() $\mathcal H^\psi (\Lambda _P) \geq \mathcal H^\psi (\mu ) = \infty $
. This affirmatively answers part of [Reference Mauldin and Urbański25, Problem 2 in §7].
$\mathcal H^\psi (\Lambda _P) \geq \mathcal H^\psi (\mu ) = \infty $
. This affirmatively answers part of [Reference Mauldin and Urbański25, Problem 2 in §7].
Theorem 2.3. Let
![]() $\mu $
be the conformal measure on
$\mu $
be the conformal measure on
![]() $\Lambda _P$
, let
$\Lambda _P$
, let
![]() $\theta = 21/40$
, and let
$\theta = 21/40$
, and let
 $$ \begin{align} \phi(x) = \frac{\log(x)\log\log(x)\log\log\log\log(x)}{\log^2\log\log(x)}\cdot \end{align} $$
$$ \begin{align} \phi(x) = \frac{\log(x)\log\log(x)\log\log\log\log(x)}{\log^2\log\log(x)}\cdot \end{align} $$
Then
We can get a stronger result for packing measure by assuming the following conjecture.
Conjecture 2.4. Let
![]() $p_n$
denote the nth prime, and let
$p_n$
denote the nth prime, and let
![]() $d_n = p_{n + 1} - p_n$
. For each
$d_n = p_{n + 1} - p_n$
. For each
![]() $k\geq 1$
let
$k\geq 1$
let
 $$ \begin{align*} R_k &{\, \stackrel{\mathrm{def}}{=}\, } \limsup_{n\to\infty} \frac{\min(d_{n+1},\ldots,d_{n + k})}{\log^2(p_n)}\cdot \end{align*} $$
$$ \begin{align*} R_k &{\, \stackrel{\mathrm{def}}{=}\, } \limsup_{n\to\infty} \frac{\min(d_{n+1},\ldots,d_{n + k})}{\log^2(p_n)}\cdot \end{align*} $$
Then
![]() $0 < R_k < \infty $
for all
$0 < R_k < \infty $
for all
![]() $k\in {\mathbb {N}}$
.
$k\in {\mathbb {N}}$
.
Remark. The case
![]() $k = 1$
of Conjecture 2.4 is known as the Cramér–Granville conjecture. Early heuristics led Harald Cramér to conjecture that it is true with
$k = 1$
of Conjecture 2.4 is known as the Cramér–Granville conjecture. Early heuristics led Harald Cramér to conjecture that it is true with
![]() $R_1 = 1$
[Reference Cramér8]. Applying Cramér’s heuristics to the case
$R_1 = 1$
[Reference Cramér8]. Applying Cramér’s heuristics to the case
![]() $k\geq 2$
of Conjecture 2.4 yields the prediction that
$k\geq 2$
of Conjecture 2.4 yields the prediction that
![]() $R_k = 1/k$
. Specifically, assume that each integer n has probability
$R_k = 1/k$
. Specifically, assume that each integer n has probability
![]() $1/{\log (n)}$
of being prime. Under this assumption, for
$1/{\log (n)}$
of being prime. Under this assumption, for
![]() $m\leq n$
the probability that no integers in an interval
$m\leq n$
the probability that no integers in an interval
![]() $({n},{n+m}]$
are prime is approximately
$({n},{n+m}]$
are prime is approximately
![]() $(1 - 1/{\log (n)})^m \asymp \exp (-{m}/{\log (n)})$
. Thus, the probability that
$(1 - 1/{\log (n)})^m \asymp \exp (-{m}/{\log (n)})$
. Thus, the probability that
![]() $d_n> m$
is approximately
$d_n> m$
is approximately
![]() $\exp (-{m}/{\log (p_n)})$
, since
$\exp (-{m}/{\log (p_n)})$
, since
![]() $d_n> m$
if and only if the interval
$d_n> m$
if and only if the interval
![]() $({p_n},{\kern-1pt}{p_n{\kern-1pt}+{\kern-1pt}m}]$
has no primes. So the probability that
$({p_n},{\kern-1pt}{p_n{\kern-1pt}+{\kern-1pt}m}]$
has no primes. So the probability that
![]() $\min (d_{n+1},\ldots ,d_{n+k}){\kern-1pt}>{\kern-1pt} m$
is approximately
$\min (d_{n+1},\ldots ,d_{n+k}){\kern-1pt}>{\kern-1pt} m$
is approximately
![]() $\exp (-{km}/{\log (p_n)})$
. Now fix a constant
$\exp (-{km}/{\log (p_n)})$
. Now fix a constant
![]() $C> 0$
. The probability that
$C> 0$
. The probability that
![]() $\min (d_{n+1},\ldots ,d_{n+k}) \geq C\log ^2(p_n)$
is approximately
$\min (d_{n+1},\ldots ,d_{n+k}) \geq C\log ^2(p_n)$
is approximately
![]() $\exp (-{kC\log ^2(p_n)}/{\log (p_n)}) = p_n^{-kC}$
. Now, by the Borel–Cantelli lemma, the probability is 1 that
$\exp (-{kC\log ^2(p_n)}/{\log (p_n)}) = p_n^{-kC}$
. Now, by the Borel–Cantelli lemma, the probability is 1 that
![]() $\min (d_{n+1},\ldots ,d_{n+k}) \geq C\log ^2(p_n)$
for infinitely many n if and only if the series
$\min (d_{n+1},\ldots ,d_{n+k}) \geq C\log ^2(p_n)$
for infinitely many n if and only if the series
![]() $\sum _n p_n^{-kC}$
diverges, which by the prime number theorem is true if and only if
$\sum _n p_n^{-kC}$
diverges, which by the prime number theorem is true if and only if
![]() $C \leq 1/k$
. It follows (under this probabilistic model) that
$C \leq 1/k$
. It follows (under this probabilistic model) that
![]() $R_k = 1/k$
, where
$R_k = 1/k$
, where
![]() $R_k$
is as in Conjecture 2.4.
$R_k$
is as in Conjecture 2.4.
However, improved heuristics now suggest that
![]() $R_1 = 2e^{-\gamma }$
, where
$R_1 = 2e^{-\gamma }$
, where
![]() $\gamma $
is the Euler–Mascheroni constant; see [Reference Granville14, Reference Granville15, Reference Pintz30]. So perhaps an appropriate correction would be
$\gamma $
is the Euler–Mascheroni constant; see [Reference Granville14, Reference Granville15, Reference Pintz30]. So perhaps an appropriate correction would be
![]() $R_k = 2 e^{-\gamma }/k$
.
$R_k = 2 e^{-\gamma }/k$
.
Theorem 2.5. If the cases
![]() $k=1,2$
of Conjecture 2.4 are true, then
$k=1,2$
of Conjecture 2.4 are true, then
![]() $\mathcal P^\psi (\mu ) \in (0,\infty )$
, where
$\mathcal P^\psi (\mu ) \in (0,\infty )$
, where
![]() $\psi $
is given by the formula
$\psi $
is given by the formula
Note that the cases
![]() $k=1,2$
of Conjecture 2.4 correspond to information about the lengths of one-sided and two-sided gaps in the primes, respectively.
$k=1,2$
of Conjecture 2.4 correspond to information about the lengths of one-sided and two-sided gaps in the primes, respectively.
Question 2.6. Determine whether (2.5) is an exact dimension function for the prime Cantor set, that is, whether
![]() $0< \mathcal P^\psi (\Lambda _P) <\infty $
.
$0< \mathcal P^\psi (\Lambda _P) <\infty $
.
2.1. Outline of the proofs
The basic idea of the proofs is to use the Rogers–Taylor–Tricot density theorem (Theorem 3.5), which relates the Hausdorff and packing measures of a measure
![]() $\mu $
to the upper and lower densities
$\mu $
to the upper and lower densities
 $$ \begin{align*} \overline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \limsup_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)},\\ \underline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \liminf_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)}\cdot \end{align*} $$
$$ \begin{align*} \overline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \limsup_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)},\\ \underline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \liminf_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)}\cdot \end{align*} $$
at
![]() $\mu $
-almost every point
$\mu $
-almost every point
![]() $x\in \mathbb R$
. We use the Roger–Taylor–Tricot density theorem as applied to the conformal measure
$x\in \mathbb R$
. We use the Roger–Taylor–Tricot density theorem as applied to the conformal measure
![]() $\mu $
. The next step is to estimate these densities using a global measure formula (Theorem 4.5), which relates the
$\mu $
. The next step is to estimate these densities using a global measure formula (Theorem 4.5), which relates the
![]() $\mu $
-measure of a ball
$\mu $
-measure of a ball
![]() $B(x,r)$
to the
$B(x,r)$
to the
![]() $\mu $
-measure of certain cylinders contained in that ball. Here, a ‘cylinder’ is a set of the form
$\mu $
-measure of certain cylinders contained in that ball. Here, a ‘cylinder’ is a set of the form
![]() $[\omega ] = \phi _\omega ([0,1])$
, where
$[\omega ] = \phi _\omega ([0,1])$
, where
![]() $\phi _\omega $
is a composition of elements of the Gauss IFS (cf. §3). This allows us to estimate
$\phi _\omega $
is a composition of elements of the Gauss IFS (cf. §3). This allows us to estimate
![]() $\overline D_\mu ^\psi (x)$
and
$\overline D_\mu ^\psi (x)$
and
![]() $\underline D_\mu ^\psi (x)$
in terms of certain sets
$\underline D_\mu ^\psi (x)$
in terms of certain sets
![]() $J_{k,\alpha ,\epsilon } \subset E$
, where E is the set of primes (see Proposition 4.6 for more details). Specifically,
$J_{k,\alpha ,\epsilon } \subset E$
, where E is the set of primes (see Proposition 4.6 for more details). Specifically,
![]() $\overline D_\mu ^\psi (x)$
and
$\overline D_\mu ^\psi (x)$
and
![]() $\underline D_\mu ^\psi (x)$
can be estimated in terms of certain sets
$\underline D_\mu ^\psi (x)$
can be estimated in terms of certain sets
![]() $S_{\alpha ,1}$
and
$S_{\alpha ,1}$
and
![]() $S_{\alpha ,-1}$
, respectively.
$S_{\alpha ,-1}$
, respectively.
Next, we need to estimate the
![]() $\mu $
-measure of x such that
$\mu $
-measure of x such that
![]() $\overline D_\mu ^\psi (x) = 0$
(respectively,
$\overline D_\mu ^\psi (x) = 0$
(respectively,
![]() $\underline D_\mu ^\psi (x) = 0$
). This is done via Lemma 4.4, which relates the
$\underline D_\mu ^\psi (x) = 0$
). This is done via Lemma 4.4, which relates the
![]() $\mu $
-measure of
$\mu $
-measure of
![]() $S_{\alpha ,1}$
(respectively,
$S_{\alpha ,1}$
(respectively,
![]() $S_{\alpha ,-1}$
) to the
$S_{\alpha ,-1}$
) to the
![]() $\mu $
-measures of
$\mu $
-measures of
![]() $J_{k,\alpha ,1}$
(respectively,
$J_{k,\alpha ,1}$
(respectively,
![]() $J_{k,\alpha ,-1}$
). Specifically, the former is
$J_{k,\alpha ,-1}$
). Specifically, the former is
![]() $0$
if and only if the latter series converges. So the next thing we need to do is estimate the series
$0$
if and only if the latter series converges. So the next thing we need to do is estimate the series
![]() $\sum _k \mu (J_{k,\alpha ,\epsilon })$
; this is done in Lemma 4.8 for the case of a general Gauss IFS
$\sum _k \mu (J_{k,\alpha ,\epsilon })$
; this is done in Lemma 4.8 for the case of a general Gauss IFS
![]() $(\phi _a)_{a\in E}$
. Finally, in §5 we perform further computations in the case where E is the set of primes, yielding Theorems 2.1, 2.3, and 2.5.
$(\phi _a)_{a\in E}$
. Finally, in §5 we perform further computations in the case where E is the set of primes, yielding Theorems 2.1, 2.3, and 2.5.
2.2. Layout of the paper
In §3 we introduce preliminaries such as the concept of Gauss IFSs and Hausdorff and packing dimensions, as well as the Rogers–Taylor–Tricot theorem and its corollary. In §4 we prove some results that hold in the general setting of Gauss IFSs, which are used to prove our main theorems but may also be interesting in their own right. Finally, in §5 we specialize to the case of the prime Gauss IFS, allowing us to prove our main theorems.
3. Preliminaries and notation
Convention 3.1. In what follows,
![]() $A \lesssim B$
means that there exists a constant
$A \lesssim B$
means that there exists a constant
![]() $C> 0$
such that
$C> 0$
such that
![]() $A \leq C B$
.
$A \leq C B$
.
![]() $A\asymp B$
means
$A\asymp B$
means
![]() $A \lesssim B \lesssim A$
.
$A \lesssim B \lesssim A$
.
![]() $A \lesssim _+ B$
means there exists a constant C such that
$A \lesssim _+ B$
means there exists a constant C such that
![]() $A \leq B + C$
.
$A \leq B + C$
.
![]() $A \lesssim _{+,\times } B$
means that there exist constants
$A \lesssim _{+,\times } B$
means that there exist constants
![]() $C_1,C_2$
such that
$C_1,C_2$
such that
![]() $A \leq C_1 B + C_2$
.
$A \leq C_1 B + C_2$
.
Convention 3.2. All measures and sets are assumed to be Borel, and measures are assumed to be locally finite. Sometimes we restate these hypotheses for emphasis.
Recall that the continued fraction expansion of an irrational number
![]() $x\in (0,1)$
is the unique sequence of positive integers
$x\in (0,1)$
is the unique sequence of positive integers
![]() $(a_n)$
such that
$(a_n)$
such that
 $$ \begin{align*} x = [0;a_1,a_2,\ldots] {\, \stackrel{\mathrm{def}}{=}\, } \cfrac{1}{a_1 + \cfrac{1}{a_2 + \ddots}} \end{align*} $$
$$ \begin{align*} x = [0;a_1,a_2,\ldots] {\, \stackrel{\mathrm{def}}{=}\, } \cfrac{1}{a_1 + \cfrac{1}{a_2 + \ddots}} \end{align*} $$
Given
![]() $E \subset {\mathbb {N}}$
, we define the set
$E \subset {\mathbb {N}}$
, we define the set
![]() $\Lambda _E$
to be the set of all irrationals in
$\Lambda _E$
to be the set of all irrationals in
![]() $(0,1)$
whose continued fraction expansions lie entirely in E. Equivalently,
$(0,1)$
whose continued fraction expansions lie entirely in E. Equivalently,
![]() $\Lambda _E$
is the image of
$\Lambda _E$
is the image of
![]() $E^{\mathbb {N}}$
under the coding map
$E^{\mathbb {N}}$
under the coding map
![]() $\pi :{\mathbb {N}}^{\mathbb {N}} \to (0,1)$
defined by
$\pi :{\mathbb {N}}^{\mathbb {N}} \to (0,1)$
defined by
![]() $\pi ((a_n)) = [0;a_1,a_2,\ldots ]$
.
$\pi ((a_n)) = [0;a_1,a_2,\ldots ]$
.
The set
![]() $\Lambda _E$
can be studied dynamically in terms of its corresponding Gauss iterated function system, that is, the collection of maps
$\Lambda _E$
can be studied dynamically in terms of its corresponding Gauss iterated function system, that is, the collection of maps
![]() $\Phi _E {\, \stackrel {\mathrm {def}}{=}\, } (\phi _a)_{a\in E}$
, where
$\Phi _E {\, \stackrel {\mathrm {def}}{=}\, } (\phi _a)_{a\in E}$
, where
(The Gauss IFS
![]() $\Phi _E$
is a special case of a conformal iterated function system (see, for example, [Reference Chousionis, Leykekhman and Urbański7, Reference Mauldin and Urbański24, Reference Mauldin and Urbański25]), but in this paper we deal only with the Gauss IFS case.) Let
$\Phi _E$
is a special case of a conformal iterated function system (see, for example, [Reference Chousionis, Leykekhman and Urbański7, Reference Mauldin and Urbański24, Reference Mauldin and Urbański25]), but in this paper we deal only with the Gauss IFS case.) Let
![]() $E^* = \bigcup _{n\geq 0} E^n$
denote the collection of finite words in the alphabet E. For each
$E^* = \bigcup _{n\geq 0} E^n$
denote the collection of finite words in the alphabet E. For each
![]() $\omega \in E^*$
, let
$\omega \in E^*$
, let
![]() $\phi _\omega = \phi _{\omega _1}\circ \cdots \circ \phi _{\omega _{|\omega |}}$
, where
$\phi _\omega = \phi _{\omega _1}\circ \cdots \circ \phi _{\omega _{|\omega |}}$
, where
![]() $|\omega |$
denotes the length of
$|\omega |$
denotes the length of
![]() $\omega $
. Then
$\omega $
. Then
Equivalently,
![]() $\pi (\omega )$
is the unique intersection point of the cylinder sets
$\pi (\omega )$
is the unique intersection point of the cylinder sets
![]() $[\omega \upharpoonleft [1,n]]$
, where
$[\omega \upharpoonleft [1,n]]$
, where
Next, we define the pressure of a real number
![]() $s \geq 0$
to be
$s \geq 0$
to be
 $$ \begin{align*} {\mathbb P}_E(s) {\, \stackrel{\mathrm{def}}{=}\, } \lim_{n\to\infty} \frac1n \log \sum_{\omega\in E^n} \|\phi_\omega'\|^s, \end{align*} $$
$$ \begin{align*} {\mathbb P}_E(s) {\, \stackrel{\mathrm{def}}{=}\, } \lim_{n\to\infty} \frac1n \log \sum_{\omega\in E^n} \|\phi_\omega'\|^s, \end{align*} $$
where
![]() $\|\phi _\omega '\| {\, \stackrel {\mathrm {def}}{=}\, } \sup _{x\in [0,1]} |\phi _\omega '(x)|$
. The Gauss IFS
$\|\phi _\omega '\| {\, \stackrel {\mathrm {def}}{=}\, } \sup _{x\in [0,1]} |\phi _\omega '(x)|$
. The Gauss IFS
![]() $\Phi _E$
is called regular if there exists
$\Phi _E$
is called regular if there exists
![]() $\delta = \delta _E \geq 0$
such that
$\delta = \delta _E \geq 0$
such that
![]() ${\mathbb P}_E(\delta _E) = 0$
. The following result was proven in [Reference Mauldin and Urbański24].
${\mathbb P}_E(\delta _E) = 0$
. The following result was proven in [Reference Mauldin and Urbański24].
Proposition 3.3. [Reference Mauldin and Urbański24, Theorem 3.5]
Let
![]() $\Phi _E$
be a regular (Gauss) IFS. Then there exists a unique measure
$\Phi _E$
be a regular (Gauss) IFS. Then there exists a unique measure
![]() $\mu = \mu _E$
on
$\mu = \mu _E$
on
![]() $\Lambda _E$
such that
$\Lambda _E$
such that
 $$ \begin{align*} \mu_E(A) = \sum_{a\in E} \int_{\phi_a^{-1}(A)} |\phi_a'(x)|^{\delta_E} \;{d}\mu_E(x) \end{align*} $$
$$ \begin{align*} \mu_E(A) = \sum_{a\in E} \int_{\phi_a^{-1}(A)} |\phi_a'(x)|^{\delta_E} \;{d}\mu_E(x) \end{align*} $$
for all
![]() $A \subset [0,1]$
.
$A \subset [0,1]$
.
The measure
![]() $\mu $
appearing in Proposition 3.3 is called the conformal measure of
$\mu $
appearing in Proposition 3.3 is called the conformal measure of
![]() $\Phi _E$
, and
$\Phi _E$
, and
![]() $\delta _E$
is called the conformal dimension of
$\delta _E$
is called the conformal dimension of
![]() $\Phi _E$
. Recall that the bounded distortion property (cf. [Reference Mauldin and Urbański24, (2.9)]) states that
$\Phi _E$
. Recall that the bounded distortion property (cf. [Reference Mauldin and Urbański24, (2.9)]) states that
This implies that the measure of a cylinder set
![]() $[\omega ]$
satisfies
$[\omega ]$
satisfies
and that
Convention 3.4. We write
![]() $\mu (A) = \sum _{\omega \in A} \mu (\omega )$
for all
$\mu (A) = \sum _{\omega \in A} \mu (\omega )$
for all
![]() $A \subset E^*$
, and
$A \subset E^*$
, and
![]() $\mu (A) = \mu (\pi (A))$
for all
$\mu (A) = \mu (\pi (A))$
for all
![]() $A \subset E^{\mathbb {N}}$
.
$A \subset E^{\mathbb {N}}$
.
The aim of this paper is to study the Hausdorff and packing measures of the measure
![]() $\mu _P$
, where
$\mu _P$
, where
![]() $P\subset {\mathbb {N}}$
is the set of primes. To define these quantities, let
$P\subset {\mathbb {N}}$
is the set of primes. To define these quantities, let
![]() $\psi :(0,\infty ) \to (0,\infty )$
be a dimension function, that is, a continuous increasing function such that
$\psi :(0,\infty ) \to (0,\infty )$
be a dimension function, that is, a continuous increasing function such that
![]() $\lim _{r\to 0} \psi (r) {\kern-1pt}={\kern-1pt} 0$
. Then the
$\lim _{r\to 0} \psi (r) {\kern-1pt}={\kern-1pt} 0$
. Then the
![]() $\psi $
-dimensional Hausdorff measure of a set
$\psi $
-dimensional Hausdorff measure of a set
![]() $A\subset \mathbb R$
is
$A\subset \mathbb R$
is
 $$ \begin{align*} \mathcal H^\psi(A){\, \stackrel{\mathrm{def}}{=}\, } \lim_{\epsilon\searrow 0} \inf\bigg\{&\sum_{i = 1}^\infty \psi(\operatorname{\mathrm{diam}}(U_i)): (U_i)_1^\infty\\ &\ \text{is a countable cover of } A \text{ with} \operatorname{\mathrm{diam}}(U_i)\leq\epsilon \text{ for all } i\bigg\} \end{align*} $$
$$ \begin{align*} \mathcal H^\psi(A){\, \stackrel{\mathrm{def}}{=}\, } \lim_{\epsilon\searrow 0} \inf\bigg\{&\sum_{i = 1}^\infty \psi(\operatorname{\mathrm{diam}}(U_i)): (U_i)_1^\infty\\ &\ \text{is a countable cover of } A \text{ with} \operatorname{\mathrm{diam}}(U_i)\leq\epsilon \text{ for all } i\bigg\} \end{align*} $$
and the
![]() $\psi $
-dimensional packing measure of A is defined by the formulas
$\psi $
-dimensional packing measure of A is defined by the formulas
 $$ \begin{align*} &\widetilde{\mathcal P}^\psi(A)\\ &\quad{\, \stackrel{\mathrm{def}}{=}\, } \lim_{\epsilon\searrow 0}\sup\bigg\{\sum_{j = 1}^\infty \psi(\operatorname{\mathrm{diam}}(B_j)): \begin{aligned} &(B_j)_1^\infty \text{is a countable disjoint collection of balls}\\ &\text{with centers in } A \text{ and with} \operatorname{\mathrm{diam}}(B_j)\leq\epsilon \text{ for all } j \end{aligned}\bigg\} \end{align*} $$
$$ \begin{align*} &\widetilde{\mathcal P}^\psi(A)\\ &\quad{\, \stackrel{\mathrm{def}}{=}\, } \lim_{\epsilon\searrow 0}\sup\bigg\{\sum_{j = 1}^\infty \psi(\operatorname{\mathrm{diam}}(B_j)): \begin{aligned} &(B_j)_1^\infty \text{is a countable disjoint collection of balls}\\ &\text{with centers in } A \text{ and with} \operatorname{\mathrm{diam}}(B_j)\leq\epsilon \text{ for all } j \end{aligned}\bigg\} \end{align*} $$
and
 $$ \begin{align*} \mathcal P^\psi(A) {\, \stackrel{\mathrm{def}}{=}\, } \inf\bigg\{ \sum_{i = 1}^\infty \widetilde{\mathcal P}^\psi(A_i) : A \subset \bigcup_{i = 1}^\infty A_i\bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal P^\psi(A) {\, \stackrel{\mathrm{def}}{=}\, } \inf\bigg\{ \sum_{i = 1}^\infty \widetilde{\mathcal P}^\psi(A_i) : A \subset \bigcup_{i = 1}^\infty A_i\bigg\}. \end{align*} $$
A special case is when
![]() $\psi (r) = r^s$
for some
$\psi (r) = r^s$
for some
![]() $s> 0$
, in which case we write
$s> 0$
, in which case we write
![]() $\mathcal H^\psi = \mathcal H^s$
and
$\mathcal H^\psi = \mathcal H^s$
and
![]() $\mathcal P^\psi = \mathcal P^s$
.
$\mathcal P^\psi = \mathcal P^s$
.
If
![]() $\mu $
is a locally finite Borel measure on
$\mu $
is a locally finite Borel measure on
![]() $\mathbb R$
, then we let
$\mathbb R$
, then we let
 $$ \begin{align*} \mathcal H^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal H^\psi(A): \mu(\mathbb R\setminus A) = 0\},\\ \mathcal P^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal P^\psi(A): \mu(\mathbb R\setminus A) = 0\}. \end{align*} $$
$$ \begin{align*} \mathcal H^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal H^\psi(A): \mu(\mathbb R\setminus A) = 0\},\\ \mathcal P^\psi(\mu) &{\, \stackrel{\mathrm{def}}{=}\, } \inf\{\mathcal P^\psi(A): \mu(\mathbb R\setminus A) = 0\}. \end{align*} $$
This is analogous to the definitions of the (upper) Hausdorff and packing dimensions of
![]() $\mu $
; see [Reference Falconer11, Proposition 10.3].
$\mu $
; see [Reference Falconer11, Proposition 10.3].
Remark. The Hausdorff and packing dimensions of sets [Reference Falconer11, §2.1] and the (upper) Hausdorff and packing dimensions of measures [Reference Falconer11, Proposition 10.3] can be defined in terms of
![]() $\mathcal H^s$
and
$\mathcal H^s$
and
![]() $\mathcal P^s$
as follows:
$\mathcal P^s$
as follows:
 $$ \begin{align*} {\dim_H}(A) &{\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal H^s(A)> 0\}, \overline{\dim_H}(\mu) {\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal H^s(\mu) > 0\},\\ {\dim_P}(A) &{\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal P^s(A) > 0\}, \overline{\dim_P}(\mu) {\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal P^s(\mu) > 0\}. \end{align*} $$
$$ \begin{align*} {\dim_H}(A) &{\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal H^s(A)> 0\}, \overline{\dim_H}(\mu) {\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal H^s(\mu) > 0\},\\ {\dim_P}(A) &{\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal P^s(A) > 0\}, \overline{\dim_P}(\mu) {\, \stackrel{\mathrm{def}}{=}\, } \sup\{s\geq 0:\mathcal P^s(\mu) > 0\}. \end{align*} $$
It follows from [Reference Mauldin and Urbański25, Theorems 2.7 and 2.11] and Theorems 2.1 and 2.3 above that
For each point
![]() $x\in \mathbb R$
let
$x\in \mathbb R$
let
 $$ \begin{align*} \overline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \limsup_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)},\\ \underline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \liminf_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)}\cdot \end{align*} $$
$$ \begin{align*} \overline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \limsup_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)},\\ \underline D_\mu^\psi(x) &{\, \stackrel{\mathrm{def}}{=}\, } \liminf_{r\searrow 0} \frac{\mu(B(x,r))}{\psi(r)}\cdot \end{align*} $$
Theorem 3.5. (Rogers–Taylor–Tricot density theorem, [Reference Taylor and Tricot39, Theorems 2.1 and 5.4]; see also [Reference Rogers and Taylor32])
Let
![]() $\mu $
be a positive and finite Borel measure on
$\mu $
be a positive and finite Borel measure on
![]() $\mathbb R$
, and let
$\mathbb R$
, and let
![]() $\psi $
be a dimension function. Then for every Borel set
$\psi $
be a dimension function. Then for every Borel set
![]() $A\subset \mathbb R$
,
$A\subset \mathbb R$
,
 $$ \begin{align} \mu(A) \inf_{x\in A}\frac{1}{\overline D_\mu^\psi(x)} \lesssim_\times \mathcal H^\psi(A) &\lesssim_\times \mu(\mathbb R) \sup_{x\in A}\frac{1}{\overline D_\mu^\psi(x)}, \end{align} $$
$$ \begin{align} \mu(A) \inf_{x\in A}\frac{1}{\overline D_\mu^\psi(x)} \lesssim_\times \mathcal H^\psi(A) &\lesssim_\times \mu(\mathbb R) \sup_{x\in A}\frac{1}{\overline D_\mu^\psi(x)}, \end{align} $$
 $$ \begin{align} \mu(A) \inf_{x\in A}\frac{1}{\underline D_\mu^\psi(x)} \lesssim_\times \mathcal P^\psi(A) &\lesssim_\times \mu(\mathbb R) \sup_{x\in A}\frac{1}{\underline D_\mu^\psi(x)}\cdot \end{align} $$
$$ \begin{align} \mu(A) \inf_{x\in A}\frac{1}{\underline D_\mu^\psi(x)} \lesssim_\times \mathcal P^\psi(A) &\lesssim_\times \mu(\mathbb R) \sup_{x\in A}\frac{1}{\underline D_\mu^\psi(x)}\cdot \end{align} $$
Corollary 3.6. Let
![]() $\mu ,\psi $
be as in Theorem 3.5. Then
$\mu ,\psi $
be as in Theorem 3.5. Then
 $$ \begin{align} \mathcal H^\psi(\mu) &\asymp_\times \operatorname*{ess\ sup}\limits_{x\sim \mu}\frac{1}{\overline D_\mu^\psi(x)}, \end{align} $$
$$ \begin{align} \mathcal H^\psi(\mu) &\asymp_\times \operatorname*{ess\ sup}\limits_{x\sim \mu}\frac{1}{\overline D_\mu^\psi(x)}, \end{align} $$
 $$ \begin{align} \mathcal P^\psi(\mu) &\asymp_\times \operatorname*{ess\ sup}\limits_{x\sim \mu}\frac{1}{\underline D_\mu^\psi(x)}\cdot \end{align} $$
$$ \begin{align} \mathcal P^\psi(\mu) &\asymp_\times \operatorname*{ess\ sup}\limits_{x\sim \mu}\frac{1}{\underline D_\mu^\psi(x)}\cdot \end{align} $$
Here the implied constants may depend on
![]() $\mu $
and
$\mu $
and
![]() $\psi $
, and
$\psi $
, and
![]() $\mathrm{ess\ sup}_{x\sim \mu }$
denotes the essential supremum with x distributed according to
$\mathrm{ess\ sup}_{x\sim \mu }$
denotes the essential supremum with x distributed according to
![]() $\mu $
.
$\mu $
.
Proof. We prove (3.4); (3.5) is similar. For the
![]() $\lesssim $
direction, take
$\lesssim $
direction, take
 $$ \begin{align*} A = \bigg\{x : \frac{1}{\overline D_\mu^\psi(x)} \leq \operatorname*{ess\ sup}_{y\sim \mu}\frac{1}{\overline D_\mu^\psi(y)}\bigg\} \end{align*} $$
$$ \begin{align*} A = \bigg\{x : \frac{1}{\overline D_\mu^\psi(x)} \leq \operatorname*{ess\ sup}_{y\sim \mu}\frac{1}{\overline D_\mu^\psi(y)}\bigg\} \end{align*} $$
in the right half of (3.2). A has full
![]() $\mu $
-measure, so
$\mu $
-measure, so
![]() $\mathcal H^\psi (\mu ) \leq \mathcal H^\psi (A)$
. For the
$\mathcal H^\psi (\mu ) \leq \mathcal H^\psi (A)$
. For the
![]() $\gtrsim $
direction, let B be a set of full
$\gtrsim $
direction, let B be a set of full
![]() $\mu $
-measure, fix
$\mu $
-measure, fix
![]() $t < {\mathrm{ess\ sup}}_{y\sim \mu }({1}/{\overline D_\mu ^\psi (y)})$
, and let
$t < {\mathrm{ess\ sup}}_{y\sim \mu }({1}/{\overline D_\mu ^\psi (y)})$
, and let
 $$ \begin{align*} A = B\cap \bigg\{x : \frac{1}{\overline D_\mu^\psi(x)} \geq t \bigg\}. \end{align*} $$
$$ \begin{align*} A = B\cap \bigg\{x : \frac{1}{\overline D_\mu^\psi(x)} \geq t \bigg\}. \end{align*} $$
Then
![]() $\mu (A)> 0$
. Applying the left half of (3.2), using
$\mu (A)> 0$
. Applying the left half of (3.2), using
![]() $\mathcal H^\psi (A) \leq \mathcal H^\psi (B)$
, and then taking the infimum over all B and supremum over t yields the
$\mathcal H^\psi (A) \leq \mathcal H^\psi (B)$
, and then taking the infimum over all B and supremum over t yields the
![]() $\gtrsim $
direction of (3.4).
$\gtrsim $
direction of (3.4).
Remark. For a doubling dimension function
![]() $\psi $
and a conformal measure
$\psi $
and a conformal measure
![]() $\mu = \mu _E$
, the
$\mu = \mu _E$
, the
![]() $\mathrm{ess\ sup}$
in (3.4)–(3.5) can be replaced by
$\mathrm{ess\ sup}$
in (3.4)–(3.5) can be replaced by
![]() $\operatorname *{\mbox {ess inf}}$
due to the ergodicity of the shift map
$\operatorname *{\mbox {ess inf}}$
due to the ergodicity of the shift map
![]() $\sigma $
with respect to
$\sigma $
with respect to
![]() $\mu $
[Reference Mauldin and Urbański24, Theorem 3.8]. Indeed, a routine calculation shows that
$\mu $
[Reference Mauldin and Urbański24, Theorem 3.8]. Indeed, a routine calculation shows that
![]() $\overline D_\mu ^\psi (x) \asymp \overline D_\mu ^\psi (\sigma (x))$
for all x, whence ergodicity implies that the function
$\overline D_\mu ^\psi (x) \asymp \overline D_\mu ^\psi (\sigma (x))$
for all x, whence ergodicity implies that the function
![]() $x\mapsto \overline D_\mu ^\psi (x)$
is constant
$x\mapsto \overline D_\mu ^\psi (x)$
is constant
![]() $\mu $
-almost everywhere, and similarly for
$\mu $
-almost everywhere, and similarly for
![]() $x\mapsto \underline D_\mu ^\psi (x)$
.
$x\mapsto \underline D_\mu ^\psi (x)$
.
Terminological note. If
![]() $\psi $
is a dimension function such that
$\psi $
is a dimension function such that
![]() $\mathcal H^\psi (A)$
(respectively,
$\mathcal H^\psi (A)$
(respectively,
![]() $\mathcal H^\psi (\mu )$
) is positive and finite, then
$\mathcal H^\psi (\mu )$
) is positive and finite, then
![]() $\psi $
is called an exact Hausdorff dimension function for A (respectively,
$\psi $
is called an exact Hausdorff dimension function for A (respectively,
![]() $\mu $
). Similar terminology applies to packing dimension.
$\mu $
). Similar terminology applies to packing dimension.
4. Results for regular Gauss IFSs
In this section we consider a regular Gauss IFS
![]() $\Phi _E$
and state some results concerning
$\Phi _E$
and state some results concerning
![]() $\mathcal H^\psi (\mu _E)$
and
$\mathcal H^\psi (\mu _E)$
and
![]() $\mathcal P^\psi (\mu _E)$
, given appropriate assumptions on E and
$\mathcal P^\psi (\mu _E)$
, given appropriate assumptions on E and
![]() $\psi $
. Throughout the section we will make use of the following assumptions, all of which hold for the prime Gauss IFS
$\psi $
. Throughout the section we will make use of the following assumptions, all of which hold for the prime Gauss IFS
![]() $\Phi _P$
.
$\Phi _P$
.
Assumption 4.1. The set
![]() $E \subset {\mathbb {N}}$
satisfies an asymptotic law
$E \subset {\mathbb {N}}$
satisfies an asymptotic law
where f is regularly varying with exponent
![]() $s\in (\delta ,2\delta )$
. (A function f is said to be regularly varying with exponent s if for all
$s\in (\delta ,2\delta )$
. (A function f is said to be regularly varying with exponent s if for all
![]() $a> 1$
, we have
$a> 1$
, we have
![]() $\lim _{x\to \infty } ({f(ax)}/{f(x)}) = a^s$
.) For example, if E is the set of primes, then by the prime number theorem
$\lim _{x\to \infty } ({f(ax)}/{f(x)}) = a^s$
.) For example, if E is the set of primes, then by the prime number theorem
![]() $f(N) = N/\log (N)$
satisfies (4.1), and f is regularly varying with exponent
$f(N) = N/\log (N)$
satisfies (4.1), and f is regularly varying with exponent
![]() $s {\kern-1pt}={\kern-1pt} 1 {\kern-1pt}\in{\kern-1pt} (\delta ,2\delta )$
, since
$s {\kern-1pt}={\kern-1pt} 1 {\kern-1pt}\in{\kern-1pt} (\delta ,2\delta )$
, since
![]() $1/2 {\kern-1pt}<{\kern-1pt} \delta _P {\kern-1pt}<{\kern-1pt} 1$
.
$1/2 {\kern-1pt}<{\kern-1pt} \delta _P {\kern-1pt}<{\kern-1pt} 1$
.
Assumption 4.2. There exists
![]() $\unicode{x3bb}> 1$
such that for all
$\unicode{x3bb}> 1$
such that for all
![]() $0 < r \leq 1$
,
$0 < r \leq 1$
,
For example, if E is the set of primes, then this assumption follows from the prime number theorem via a routine calculation showing that both sides are
![]() $\asymp {r^\delta }/{\log (1/r)}$
.
$\asymp {r^\delta }/{\log (1/r)}$
.
Assumption 4.3. The Lyapunov exponent
![]() $-\sum _{a\in E} \mu (a) \log \|\phi _a'\|$
is finite. Note that this is satisfied when E is the set of primes, since
$-\sum _{a\in E} \mu (a) \log \|\phi _a'\|$
is finite. Note that this is satisfied when E is the set of primes, since
![]() $\mu (a) \log \|\phi _a'\| \asymp a^{-2\delta } \log (a)$
and
$\mu (a) \log \|\phi _a'\| \asymp a^{-2\delta } \log (a)$
and
![]() $\delta> 1/2$
.
$\delta> 1/2$
.
For each
![]() $k\in {\mathbb {N}}$
, let
$k\in {\mathbb {N}}$
, let
Note that although the sets
![]() $([\omega ])_{\omega \in W_k}$
are not necessarily disjoint, there is a uniform bound (depending on
$([\omega ])_{\omega \in W_k}$
are not necessarily disjoint, there is a uniform bound (depending on
![]() $\unicode{x3bb} $
) on the multiplicity of the collection, that is, there exists a constant C independent of k such that
$\unicode{x3bb} $
) on the multiplicity of the collection, that is, there exists a constant C independent of k such that
![]() $\sup _x\{\#\{\omega \in W_k : x\in [\omega ]\}\} \leq C$
.
$\sup _x\{\#\{\omega \in W_k : x\in [\omega ]\}\} \leq C$
.
Lemma 4.4. Assume that Assumption 4.2 holds. Let
![]() ${\mathcal {J}} = (J_k)_1^\infty $
be a sequence of subsets of E, and let
${\mathcal {J}} = (J_k)_1^\infty $
be a sequence of subsets of E, and let
 $$ \begin{align*} \Sigma_{\mathcal{J}} &{\, \stackrel{{\mathrm{def}}}{=}\, } \sum_{k = 1}^\infty \mu(J_k),\\ S_{\mathcal{J}} &{\, \stackrel{{\mathrm{def}}}{=}\, } \{\omega \in E^{\mathbb{N}} : \text{ there exist infinitely many}\ (n,k)\text{ such that } \omega\upharpoonleft n \in W_k, \omega_{n + 1} \in J_k\}. \end{align*} $$
$$ \begin{align*} \Sigma_{\mathcal{J}} &{\, \stackrel{{\mathrm{def}}}{=}\, } \sum_{k = 1}^\infty \mu(J_k),\\ S_{\mathcal{J}} &{\, \stackrel{{\mathrm{def}}}{=}\, } \{\omega \in E^{\mathbb{N}} : \text{ there exist infinitely many}\ (n,k)\text{ such that } \omega\upharpoonleft n \in W_k, \omega_{n + 1} \in J_k\}. \end{align*} $$
Then
![]() $\mu (S_{\mathcal {J}})> 0$
if
$\mu (S_{\mathcal {J}})> 0$
if
![]() $\Sigma _{\mathcal {J}} = \infty $
, and
$\Sigma _{\mathcal {J}} = \infty $
, and
![]() $\mu (S_{\mathcal {J}})=0$
otherwise.
$\mu (S_{\mathcal {J}})=0$
otherwise.
Proof. For each
![]() $k\in {\mathbb {N}}$
, let
$k\in {\mathbb {N}}$
, let
We claim that
-
(1)
 $\mu (A_k) \asymp \mu (J_k)$
and that
$\mu (A_k) \asymp \mu (J_k)$
and that -
(2) the sequence
 $(A_k)_1^\infty $
is quasi-independent, meaning that
$(A_k)_1^\infty $
is quasi-independent, meaning that
 $\mu (A_k \cap A_\ell ) \lesssim \mu (A_k) \mu (A_\ell )$
whenever
$\mu (A_k \cap A_\ell ) \lesssim \mu (A_k) \mu (A_\ell )$
whenever
 $k\neq \ell $
.
$k\neq \ell $
.
Proof of (1). Since the collection
![]() $([\omega ])_{\omega \in W_k}$
has bounded multiplicity, we have
$([\omega ])_{\omega \in W_k}$
has bounded multiplicity, we have
 $$ \begin{align*} \mu(A_k) \asymp \sum_{\omega\in W_k} \sum_{a\in J_k} \mu(\omega a) \asymp \sum_{\omega\in W_k} \mu(\omega)\mu(J_k) \end{align*} $$
$$ \begin{align*} \mu(A_k) \asymp \sum_{\omega\in W_k} \sum_{a\in J_k} \mu(\omega a) \asymp \sum_{\omega\in W_k} \mu(\omega)\mu(J_k) \end{align*} $$
and
 $$ \begin{align*} \sum_{\omega\in W_k} \mu(\omega) & \asymp {\sum_{\substack{\omega \in W_{k} \|\phi_{{\omega}\upharpoonleft|\omega| - 1}'\|> \unicode{x3bb}^{-k}}}} \mu(\omega)\quad (\text{since} ([\omega])_{\omega\in W_k} \text{has bounded multiplicity)} \\ & \asymp {\sum_{\substack{\omega\in E^* \|\phi_\omega'\| > \unicode{x3bb}^{-k}}}} {\sum_{\substack{a\in E \omega a \in W_k}}} \mu(\omega) \mu(a)\\ & \asymp {\sum_{\substack{\omega\in E^* \|\phi_\omega'\| > \unicode{x3bb}^{-k}}}} \mu(\omega) {\sum_{\substack{a\in E \|\phi_{\omega a}'\| \leq \unicode{x3bb}^{-k}}}} \mu(a) \quad \text{(by {Assumption 4.2})}\\ & \asymp {\sum_{\substack{\omega\in E^* \ \|\phi_\omega'\| > \unicode{x3bb}^{-k}}}} {\sum_{\substack{a\in E \|\phi_{\omega a}'\|\leq \unicode{x3bb}^{-k}}}} \mu(\omega a) = \mu([0,1]) = 1. \end{align*} $$
$$ \begin{align*} \sum_{\omega\in W_k} \mu(\omega) & \asymp {\sum_{\substack{\omega \in W_{k} \|\phi_{{\omega}\upharpoonleft|\omega| - 1}'\|> \unicode{x3bb}^{-k}}}} \mu(\omega)\quad (\text{since} ([\omega])_{\omega\in W_k} \text{has bounded multiplicity)} \\ & \asymp {\sum_{\substack{\omega\in E^* \|\phi_\omega'\| > \unicode{x3bb}^{-k}}}} {\sum_{\substack{a\in E \omega a \in W_k}}} \mu(\omega) \mu(a)\\ & \asymp {\sum_{\substack{\omega\in E^* \|\phi_\omega'\| > \unicode{x3bb}^{-k}}}} \mu(\omega) {\sum_{\substack{a\in E \|\phi_{\omega a}'\| \leq \unicode{x3bb}^{-k}}}} \mu(a) \quad \text{(by {Assumption 4.2})}\\ & \asymp {\sum_{\substack{\omega\in E^* \ \|\phi_\omega'\| > \unicode{x3bb}^{-k}}}} {\sum_{\substack{a\in E \|\phi_{\omega a}'\|\leq \unicode{x3bb}^{-k}}}} \mu(\omega a) = \mu([0,1]) = 1. \end{align*} $$
Proof of (2). Let
![]() $k < \ell $
. Then
$k < \ell $
. Then
 $$ \begin{align*} \mu(A_k\cap A_\ell) &= \sum_{\omega\in W_k} \sum_{a\in J_k} \sum_{\substack{\tau\in E^* \omega a \tau \in W_\ell}} \sum_{b\in J_\ell} \mu(\omega a \tau b)\\ &\asymp \sum_{\omega\in W_k} \mu(\omega) \sum_{a\in J_k} \mu(a) \sum_{\substack{\tau\in E^* \omega a \tau \in W_\ell}} \mu(\tau) \mu(J_\ell)\\ &\lesssim \mu(J_k) \mu(J_\ell) \asymp \mu(A_k) \mu(A_\ell), \end{align*} $$
$$ \begin{align*} \mu(A_k\cap A_\ell) &= \sum_{\omega\in W_k} \sum_{a\in J_k} \sum_{\substack{\tau\in E^* \omega a \tau \in W_\ell}} \sum_{b\in J_\ell} \mu(\omega a \tau b)\\ &\asymp \sum_{\omega\in W_k} \mu(\omega) \sum_{a\in J_k} \mu(a) \sum_{\substack{\tau\in E^* \omega a \tau \in W_\ell}} \mu(\tau) \mu(J_\ell)\\ &\lesssim \mu(J_k) \mu(J_\ell) \asymp \mu(A_k) \mu(A_\ell), \end{align*} $$
where the
![]() $\lesssim $
in the last line is because the collection
$\lesssim $
in the last line is because the collection
![]() $\{[\tau ] : \tau \in E^*, \omega a \tau \in W_\ell \}$
has bounded multiplicity.
$\{[\tau ] : \tau \in E^*, \omega a \tau \in W_\ell \}$
has bounded multiplicity.
Now if
![]() $\sum _k \mu (J_k) < \infty $
, the convergence case of the Borel–Cantelli lemma completes the proof. If
$\sum _k \mu (J_k) < \infty $
, the convergence case of the Borel–Cantelli lemma completes the proof. If
![]() $\sum _k \mu (J_k) = \infty $
, then (2) implies that condition [Reference Beresnevich and Velani5, (3)] holds, so [Reference Beresnevich and Velani5, Lemma DBC] completes the proof.
$\sum _k \mu (J_k) = \infty $
, then (2) implies that condition [Reference Beresnevich and Velani5, (3)] holds, so [Reference Beresnevich and Velani5, Lemma DBC] completes the proof.
Theorem 4.5. (Global measure formula for Gauss IFSs)
Let
![]() $\Phi _E$
be a regular Gauss IFS. Then for all
$\Phi _E$
be a regular Gauss IFS. Then for all
![]() $x = \pi (\omega ) \in \Lambda _E$
and
$x = \pi (\omega ) \in \Lambda _E$
and
![]() $r> 0$
, there exists n such that
$r> 0$
, there exists n such that
and
where
 $$ \begin{align*} M(x,n,r) {\, \stackrel{\mathrm{def}}{=}\, } \sum_{\substack{a\in E \\ [(\omega\upharpoonleft n) a] \subset B(x,r)}} \mu((\omega\upharpoonleft n) a), \end{align*} $$
$$ \begin{align*} M(x,n,r) {\, \stackrel{\mathrm{def}}{=}\, } \sum_{\substack{a\in E \\ [(\omega\upharpoonleft n) a] \subset B(x,r)}} \mu((\omega\upharpoonleft n) a), \end{align*} $$
and where
![]() $C\geq 1$
is a uniform constant.
$C\geq 1$
is a uniform constant.
We call this theorem a ‘global measure formula’ due to its similarity to other global measure formulas found in the literature, such as [Reference Sullivan37, §7], [Reference Stratmann and Velani36, Theorem 2].
Proof. Note that the first inequality
![]() $M(x,n,r) \leq \mu (B(x,r))$
follows trivially from applying
$M(x,n,r) \leq \mu (B(x,r))$
follows trivially from applying
![]() $\mu $
to both sides of the inclusion
$\mu $
to both sides of the inclusion
![]() $\bigcup \{[\tau a] \subset B(x,r) : a\in E\} \subset B(x,r)$
.
$\bigcup \{[\tau a] \subset B(x,r) : a\in E\} \subset B(x,r)$
.
Given
![]() $x = \pi (\omega ) \in \Lambda _E$
and
$x = \pi (\omega ) \in \Lambda _E$
and
![]() $r> 0$
, let
$r> 0$
, let
![]() $m\geq 0$
be maximal such that
$m\geq 0$
be maximal such that
![]() $B(x,r)\cap \Lambda _E \subset [\omega \upharpoonleft m]$
. By applying the inverse transformation
$B(x,r)\cap \Lambda _E \subset [\omega \upharpoonleft m]$
. By applying the inverse transformation
![]() $\phi _{\omega \upharpoonleft m}^{-1}$
to the setup and using the bounded distortion property we may without loss of generality assume that
$\phi _{\omega \upharpoonleft m}^{-1}$
to the setup and using the bounded distortion property we may without loss of generality assume that
![]() $m = 0$
, or equivalently that
$m = 0$
, or equivalently that
![]() $B(x,r)$
intersects at least two top-level cylinders. We now divide into two cases.
$B(x,r)$
intersects at least two top-level cylinders. We now divide into two cases.
-
• If
 $[\omega _1] \subset B(x,r)$
, then we claim that which guarantees (4.4) with
$[\omega _1] \subset B(x,r)$
, then we claim that which guarantees (4.4) with $$ \begin{align*} B(x,r)\cap \Lambda_E \subset \bigcup_{\substack{a\in E \\ [a] \subset B(x,Cr)}} [a] \end{align*} $$
$$ \begin{align*} B(x,r)\cap \Lambda_E \subset \bigcup_{\substack{a\in E \\ [a] \subset B(x,Cr)}} [a] \end{align*} $$
 $n=0$
. Indeed, if
$n=0$
. Indeed, if
 $y = \pi (\tau ) \in B(x,r)\cap \Lambda _E$
, then
$y = \pi (\tau ) \in B(x,r)\cap \Lambda _E$
, then
 $1/({\tau _1+1}) \leq \pi (\tau ) \leq \pi (\omega ) + r \leq 1/{\omega _1} + r$
and thus
$1/({\tau _1+1}) \leq \pi (\tau ) \leq \pi (\omega ) + r \leq 1/{\omega _1} + r$
and thus  $$ \begin{align*} \operatorname{\mathrm{diam}}([\tau_1]) &\asymp \frac1{\tau_1^2} \lesssim \max\bigg(\frac1{\omega_1^2},r^2\bigg)\\ &\asymp \operatorname{\mathrm{diam}}([\omega_1]) + r^2 \leq 2r + r^2 \lesssim r. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{diam}}([\tau_1]) &\asymp \frac1{\tau_1^2} \lesssim \max\bigg(\frac1{\omega_1^2},r^2\bigg)\\ &\asymp \operatorname{\mathrm{diam}}([\omega_1]) + r^2 \leq 2r + r^2 \lesssim r. \end{align*} $$
-
• If
 $[\omega _1]$
is not contained in
$[\omega _1]$
is not contained in
 $B(x,r)$
, then one of the endpoints of
$B(x,r)$
, then one of the endpoints of
 $[\omega _1]$
, namely
$[\omega _1]$
, namely
 $1/\omega _1$
or
$1/\omega _1$
or
 $1/(\omega _1+1)$
, is contained in
$1/(\omega _1+1)$
, is contained in
 $B(x,r)$
, but not both. Suppose that
$B(x,r)$
, but not both. Suppose that
 $1/\omega _1 \in B(x,r)$
; the other case is similar. Now for all
$1/\omega _1 \in B(x,r)$
; the other case is similar. Now for all
 $N\in E$
such that
$N\in E$
such that
 $[(\omega _1 - 1)*1*N]\cap B(x,r)\neq \emptyset $
(where
$[(\omega _1 - 1)*1*N]\cap B(x,r)\neq \emptyset $
(where
 $*$
denotes concatenation), we have and thus
$*$
denotes concatenation), we have and thus $$ \begin{align*} r\geq d(1/\omega_1,[(\omega_1-1)*1*N]) \asymp 1/(\omega_1^2 N) \asymp d(1/\omega_1,\min([\omega_1*N])) \end{align*} $$
$$ \begin{align*} r\geq d(1/\omega_1,[(\omega_1-1)*1*N]) \asymp 1/(\omega_1^2 N) \asymp d(1/\omega_1,\min([\omega_1*N])) \end{align*} $$
 $[\omega _1*N] \subset B(1/\omega _1,Cr) \subset B(x,(C+1)r)$
for an appropriately large constant C. Applying
$[\omega _1*N] \subset B(1/\omega _1,Cr) \subset B(x,(C+1)r)$
for an appropriately large constant C. Applying
 $\mu $
and summing over all such N gives which implies (4.4) with
$\mu $
and summing over all such N gives which implies (4.4) with $$ \begin{align*} \mu(B(x,r)) &\leq \mu([\omega_1]\cap B(x,r)) + \sum_{\substack{N\in E \\ [(\omega_1 - 1)*1*N]\cap B(x,r)\neq {\emptyset}}} \mu([(\omega_1 - 1)*1*N])\\ &\lesssim \sum_{\substack{N\in E \\ [\omega_1*N] \subset B(x,(C+1)r)}} \mu([\omega_1*N]) \end{align*} $$
$$ \begin{align*} \mu(B(x,r)) &\leq \mu([\omega_1]\cap B(x,r)) + \sum_{\substack{N\in E \\ [(\omega_1 - 1)*1*N]\cap B(x,r)\neq {\emptyset}}} \mu([(\omega_1 - 1)*1*N])\\ &\lesssim \sum_{\substack{N\in E \\ [\omega_1*N] \subset B(x,(C+1)r)}} \mu([\omega_1*N]) \end{align*} $$
 $n=1$
. On the other hand, since we have
$n=1$
. On the other hand, since we have $$ \begin{align*} r\geq d(x,1/\omega_1) \asymp 1/(\omega_1^2 \omega_2) \geq 1/(\omega_1^2 \omega_2^2) \asymp \operatorname{\mathrm{diam}}([\omega\upharpoonleft 2]), \end{align*} $$
$$ \begin{align*} r\geq d(x,1/\omega_1) \asymp 1/(\omega_1^2 \omega_2) \geq 1/(\omega_1^2 \omega_2^2) \asymp \operatorname{\mathrm{diam}}([\omega\upharpoonleft 2]), \end{align*} $$
 $[\omega \upharpoonleft 2]\subset B(x,C r)$
as long as C is sufficiently large.
$[\omega \upharpoonleft 2]\subset B(x,C r)$
as long as C is sufficiently large.
Fix
![]() $\epsilon \in \{\pm 1\}$
(loosely speaking,
$\epsilon \in \{\pm 1\}$
(loosely speaking,
![]() $\epsilon =1$
when we are trying to prove results about Hausdorff measure, and
$\epsilon =1$
when we are trying to prove results about Hausdorff measure, and
![]() $\epsilon =-1$
when we are trying to prove results about packing measure), a real number
$\epsilon =-1$
when we are trying to prove results about packing measure), a real number
![]() $\alpha> 0$
, and a doubling dimension function
$\alpha> 0$
, and a doubling dimension function
![]() $\psi (r) = r^\delta \Psi (r)$
. We will assume that
$\psi (r) = r^\delta \Psi (r)$
. We will assume that
![]() $\Psi $
is
$\Psi $
is
![]() $\epsilon $
-monotonic, meaning that
$\epsilon $
-monotonic, meaning that
![]() $\Psi $
is decreasing if
$\Psi $
is decreasing if
![]() $\epsilon =1$
and increasing if
$\epsilon =1$
and increasing if
![]() $\epsilon =-1$
. Fix
$\epsilon =-1$
. Fix
![]() $\alpha> 0$
, and for each
$\alpha> 0$
, and for each
![]() $k\in {\mathbb {N}}$
let
$k\in {\mathbb {N}}$
let
Here
![]() $\lesseqgtr $
denotes
$\lesseqgtr $
denotes
![]() $\geq $
if
$\geq $
if
![]() $\epsilon =1$
and
$\epsilon =1$
and
![]() $\leq $
if
$\leq $
if
![]() $\epsilon =-1$
, and
$\epsilon =-1$
, and
![]() $\unicode{x3bb}> 1$
is as in Assumption 4.2. Write
$\unicode{x3bb}> 1$
is as in Assumption 4.2. Write
as defined in Lemma 4.4. Note that
![]() $S_{\alpha ,1}$
grows smaller as
$S_{\alpha ,1}$
grows smaller as
![]() $\alpha $
grows larger, while
$\alpha $
grows larger, while
![]() $S_{\alpha ,-1}$
grows larger as
$S_{\alpha ,-1}$
grows larger as
![]() $\alpha $
grows larger.
$\alpha $
grows larger.
Proposition 4.6. For all
![]() $\omega \in E^{\mathbb {N}}$
,
$\omega \in E^{\mathbb {N}}$
,
 $$ \begin{align*} \sup\{\alpha : \omega\in S_{\alpha,1}\} &\asymp \overline D_\mu^\psi(\pi(\omega)),\\ \inf\{\alpha : \omega\in S_{\alpha,-1}\} &\asymp \underline D_\mu^\psi(\pi(\omega)). \end{align*} $$
$$ \begin{align*} \sup\{\alpha : \omega\in S_{\alpha,1}\} &\asymp \overline D_\mu^\psi(\pi(\omega)),\\ \inf\{\alpha : \omega\in S_{\alpha,-1}\} &\asymp \underline D_\mu^\psi(\pi(\omega)). \end{align*} $$
Proof. Let
![]() $x = \pi (\omega )$
, fix
$x = \pi (\omega )$
, fix
![]() $r> 0$
, and let C, n, and
$r> 0$
, and let C, n, and
![]() $\tau = \omega \upharpoonleft n$
be as in the global measure formula. Write
$\tau = \omega \upharpoonleft n$
be as in the global measure formula. Write
![]() $\tau \in W_k$
for some k, as in (4.2). By the global measure formula, we have
$\tau \in W_k$
for some k, as in (4.2). By the global measure formula, we have
 $$ \begin{align*} \sum_{\substack{a\in E \\ [\tau a] \subset B(x,r)}} \mu(\tau a) \leq \mu(B(x,r)) \lesssim \sum_{\substack{a\in E \\ [\tau a] \subset B(x,Cr)}} \mu(\tau a). \end{align*} $$
$$ \begin{align*} \sum_{\substack{a\in E \\ [\tau a] \subset B(x,r)}} \mu(\tau a) \leq \mu(B(x,r)) \lesssim \sum_{\substack{a\in E \\ [\tau a] \subset B(x,Cr)}} \mu(\tau a). \end{align*} $$
Now for each
![]() $\beta \geq 1$
let
$\beta \geq 1$
let
Let
![]() $y = \pi (\sigma ^n \omega )$
, where
$y = \pi (\sigma ^n \omega )$
, where
![]() $\sigma : E^{\mathbb {N}} \to E^{\mathbb {N}}$
is the shift map. Then there exist constants
$\sigma : E^{\mathbb {N}} \to E^{\mathbb {N}}$
is the shift map. Then there exist constants
![]() $C_2,C_3> 0$
(independent of x, r, n, and k) such that for all
$C_2,C_3> 0$
(independent of x, r, n, and k) such that for all
![]() $s> 0$
,
$s> 0$
,
Taking
![]() $s = C_3^{-1}\unicode{x3bb} ^k r$
and
$s = C_3^{-1}\unicode{x3bb} ^k r$
and
![]() $s = C_2^{-1} C \unicode{x3bb} ^k \beta r$
, and using the bounded distortion property and the fact that
$s = C_2^{-1} C \unicode{x3bb} ^k \beta r$
, and using the bounded distortion property and the fact that
![]() $\mu (\tau ) \asymp \unicode{x3bb} ^{-\delta k}$
, yields
$\mu (\tau ) \asymp \unicode{x3bb} ^{-\delta k}$
, yields
 $$ \begin{align*} \Theta_1 &\lesssim \frac{1}{\psi(r)} \unicode{x3bb}^{-\delta k} \sum_{\substack{a\in E \\ [a] \subset B(y,C_2^{-1} C \unicode{x3bb}^k r)}} \mu(a),\\ \Theta_\beta &\gtrsim_\beta \frac{1}{\psi(r)} \unicode{x3bb}^{-\delta k} \sum_{\substack{a\in E \\ [a] \subset B(y,C_3^{-1} \unicode{x3bb}^k \beta r)}} \mu(a). \end{align*} $$
$$ \begin{align*} \Theta_1 &\lesssim \frac{1}{\psi(r)} \unicode{x3bb}^{-\delta k} \sum_{\substack{a\in E \\ [a] \subset B(y,C_2^{-1} C \unicode{x3bb}^k r)}} \mu(a),\\ \Theta_\beta &\gtrsim_\beta \frac{1}{\psi(r)} \unicode{x3bb}^{-\delta k} \sum_{\substack{a\in E \\ [a] \subset B(y,C_3^{-1} \unicode{x3bb}^k \beta r)}} \mu(a). \end{align*} $$
Write
![]() $b = \omega _{n + 1}$
, so that
$b = \omega _{n + 1}$
, so that
![]() $x\in [\tau b] \subset B(x,C r)$
by (4.3) and thus by the bounded distortion property
$x\in [\tau b] \subset B(x,C r)$
by (4.3) and thus by the bounded distortion property
![]() $y \in [b] \subset B(y,C_4 \unicode{x3bb} ^k r)$
for sufficiently large
$y \in [b] \subset B(y,C_4 \unicode{x3bb} ^k r)$
for sufficiently large
![]() $C_4$
. Then
$C_4$
. Then
![]() $R {\, \stackrel {\mathrm {def}}{=}\, } 2C_4 \unicode{x3bb} ^k r \geq \operatorname {\mathrm {diam}}([b])$
. Thus,
$R {\, \stackrel {\mathrm {def}}{=}\, } 2C_4 \unicode{x3bb} ^k r \geq \operatorname {\mathrm {diam}}([b])$
. Thus,
so
![]() $\Theta _1 \lesssim \Xi \lesssim _\beta \Theta _\beta $
for some
$\Theta _1 \lesssim \Xi \lesssim _\beta \Theta _\beta $
for some
![]() $C_5,C_6> 0$
, where
$C_5,C_6> 0$
, where
 $$ \begin{align*} \Xi {\, \stackrel{\mathrm{def}}{=}\, } \frac{1}{\psi(\unicode{x3bb}^{-k} R)} \unicode{x3bb}^{-\delta k} \sum_{\substack{a\in E \\ [a] \subset B([b],R)}} \mu(a) = \frac{1}{\Psi(\unicode{x3bb}^{-k} R)} R^{-\delta} \sum_{\substack{a\in E \\ [a] \subset B([b],R)}} \mu(a). \end{align*} $$
$$ \begin{align*} \Xi {\, \stackrel{\mathrm{def}}{=}\, } \frac{1}{\psi(\unicode{x3bb}^{-k} R)} \unicode{x3bb}^{-\delta k} \sum_{\substack{a\in E \\ [a] \subset B([b],R)}} \mu(a) = \frac{1}{\Psi(\unicode{x3bb}^{-k} R)} R^{-\delta} \sum_{\substack{a\in E \\ [a] \subset B([b],R)}} \mu(a). \end{align*} $$
Applying the global measure formula again yields
for some
![]() $C_7,C_8> 0$
, and thus
$C_7,C_8> 0$
, and thus
 $$ \begin{align*} \Theta_1 \geq C_9 \alpha \Rightarrow R^{-\delta} \mu(B([b],R)) \geq \alpha \Psi(\unicode{x3bb}^{-k} R) \Rightarrow \Theta_\beta \geq C_{10} \alpha,\\\Theta_\beta \leq C_{11} \alpha \Rightarrow R^{-\delta} \mu(B([b],R)) \leq \alpha \Psi(\unicode{x3bb}^{-k} R) \Rightarrow \Theta_1 \leq C_{12} \alpha \end{align*} $$
$$ \begin{align*} \Theta_1 \geq C_9 \alpha \Rightarrow R^{-\delta} \mu(B([b],R)) \geq \alpha \Psi(\unicode{x3bb}^{-k} R) \Rightarrow \Theta_\beta \geq C_{10} \alpha,\\\Theta_\beta \leq C_{11} \alpha \Rightarrow R^{-\delta} \mu(B([b],R)) \leq \alpha \Psi(\unicode{x3bb}^{-k} R) \Rightarrow \Theta_1 \leq C_{12} \alpha \end{align*} $$
for some
![]() $C_9,C_{10},C_{11},C_{12}> 0$
and for all
$C_9,C_{10},C_{11},C_{12}> 0$
and for all
![]() $\alpha> 0$
. It follows that
$\alpha> 0$
. It follows that
 $$ \begin{align*} &\overline D_\mu^\psi(\pi(\omega)) \geq C_{13} \alpha \Rightarrow \omega\in S_{\alpha,1} \Rightarrow \overline D_\mu^\psi(\pi(\omega)) \geq C_{14} \alpha,\\ &\underline D_\mu^\psi(\pi(\omega)) \leq C_{15} \alpha \Rightarrow \omega\in S_{\alpha,-1} \Rightarrow \underline D_\mu^\psi(\pi(\omega)) \leq C_{16} \alpha, \end{align*} $$
$$ \begin{align*} &\overline D_\mu^\psi(\pi(\omega)) \geq C_{13} \alpha \Rightarrow \omega\in S_{\alpha,1} \Rightarrow \overline D_\mu^\psi(\pi(\omega)) \geq C_{14} \alpha,\\ &\underline D_\mu^\psi(\pi(\omega)) \leq C_{15} \alpha \Rightarrow \omega\in S_{\alpha,-1} \Rightarrow \underline D_\mu^\psi(\pi(\omega)) \leq C_{16} \alpha, \end{align*} $$
since
![]() $\omega \in S_{\alpha ,\epsilon }$
if and only if there exist infinitely many
$\omega \in S_{\alpha ,\epsilon }$
if and only if there exist infinitely many
![]() $n,k,R$
such that
$n,k,R$
such that
![]() $\omega \upharpoonleft n \in W_k$
,
$\omega \upharpoonleft n \in W_k$
,
![]() $R\in [\|\phi _{\omega _{n+1}}'\|,1]$
, and
$R\in [\|\phi _{\omega _{n+1}}'\|,1]$
, and
![]() $R^{-\delta } \mu (B([b],R)) \lesseqgtr \alpha \Psi (\unicode{x3bb} ^{-k} R)$
, and
$R^{-\delta } \mu (B([b],R)) \lesseqgtr \alpha \Psi (\unicode{x3bb} ^{-k} R)$
, and
![]() $\limsup _{r\searrow 0} \Theta _1 = \limsup _{r\searrow 0} \Theta _\beta = \overline D_\mu ^\psi (\pi (\omega ))$
and
$\limsup _{r\searrow 0} \Theta _1 = \limsup _{r\searrow 0} \Theta _\beta = \overline D_\mu ^\psi (\pi (\omega ))$
and
![]() $\liminf _{r\searrow 0} \Theta _1 = \liminf _{r\searrow 0} \Theta _\beta = \underline D_\mu ^\psi (\pi (\omega ))$
. Taking the supremum (respectively, infimum) with respect to
$\liminf _{r\searrow 0} \Theta _1 = \liminf _{r\searrow 0} \Theta _\beta = \underline D_\mu ^\psi (\pi (\omega ))$
. Taking the supremum (respectively, infimum) with respect to
![]() $\alpha $
completes the proof.
$\alpha $
completes the proof.
So to calculate
![]() $\mathcal H^\psi (\mu )$
or
$\mathcal H^\psi (\mu )$
or
![]() $\mathcal P^\psi (\mu )$
, we need to determine whether the series
$\mathcal P^\psi (\mu )$
, we need to determine whether the series
![]() $\Sigma _{\alpha ,\epsilon } {\, \stackrel {\mathrm {def}}{=}\, } \sum _{k = 1}^\infty \mu (J_{k,\alpha ,\epsilon })$
converges or diverges for each
$\Sigma _{\alpha ,\epsilon } {\, \stackrel {\mathrm {def}}{=}\, } \sum _{k = 1}^\infty \mu (J_{k,\alpha ,\epsilon })$
converges or diverges for each
![]() $\alpha> 0$
.
$\alpha> 0$
.
Lemma 4.7. Let
![]() $\epsilon =1$
, and suppose that
$\epsilon =1$
, and suppose that
![]() $\Psi $
is
$\Psi $
is
![]() $\epsilon $
-monotonic. If
$\epsilon $
-monotonic. If
![]() $\sum _{k = 1}^\infty \mu (J_{k,\alpha ,\epsilon })$
converges (respectively, diverges) for all
$\sum _{k = 1}^\infty \mu (J_{k,\alpha ,\epsilon })$
converges (respectively, diverges) for all
![]() $\alpha> 0$
, then
$\alpha> 0$
, then
![]() $\mathcal H^\psi (\mu )=\infty $
(respectively,
$\mathcal H^\psi (\mu )=\infty $
(respectively,
![]() $=0$
); otherwise
$=0$
); otherwise
![]() $\mathcal H^\psi (\mu )$
is positive and finite. If
$\mathcal H^\psi (\mu )$
is positive and finite. If
![]() $\epsilon =-1$
, the analogous statement holds for
$\epsilon =-1$
, the analogous statement holds for
![]() $\mathcal P^\psi (\mu )$
.
$\mathcal P^\psi (\mu )$
.
Proof. By Corollary 3.6 (and the subsequent remark), it suffices to show that
![]() ${\overline D_\mu ^\psi (\pi (\omega )) = 0}$
(respectively,
${\overline D_\mu ^\psi (\pi (\omega )) = 0}$
(respectively,
![]() $=\infty $
) for a positive
$=\infty $
) for a positive
![]() $\mu $
-measure set of
$\mu $
-measure set of
![]() $\omega $
s. By Proposition 4.6, this is equivalent to showing that
$\omega $
s. By Proposition 4.6, this is equivalent to showing that
![]() $\sup \{\alpha : \omega \in S_{\alpha ,1}\} = 0$
(respectively,
$\sup \{\alpha : \omega \in S_{\alpha ,1}\} = 0$
(respectively,
![]() $=\infty $
), or equivalently that
$=\infty $
), or equivalently that
![]() $\omega \notin S_{\alpha ,1}$
(respectively,
$\omega \notin S_{\alpha ,1}$
(respectively,
![]() $\in S_{\alpha ,1}$
) for all
$\in S_{\alpha ,1}$
) for all
![]() $\alpha> 0$
. For each
$\alpha> 0$
. For each
![]() $\alpha $
, to show this for a positive
$\alpha $
, to show this for a positive
![]() $\mu $
-measure set of
$\mu $
-measure set of
![]() $\omega $
s it suffices to show that
$\omega $
s it suffices to show that
![]() $\mu (S_{\alpha ,1}) = 0$
(respectively,
$\mu (S_{\alpha ,1}) = 0$
(respectively,
![]() $>0$
), which by Lemma 4.4 is equivalent to showing that
$>0$
), which by Lemma 4.4 is equivalent to showing that
![]() $\sum _{k=1}^\infty \mu (J_{k,\alpha ,1})$
converges (respectively, diverges). The cases
$\sum _{k=1}^\infty \mu (J_{k,\alpha ,1})$
converges (respectively, diverges). The cases
![]() $\epsilon = -1$
and where
$\epsilon = -1$
and where
![]() $\sum _{k=1}^\infty \mu (J_{k,\alpha ,\epsilon })$
converges for some
$\sum _{k=1}^\infty \mu (J_{k,\alpha ,\epsilon })$
converges for some
![]() $\alpha $
but diverges for others are proven similarly.
$\alpha $
but diverges for others are proven similarly.
Lemma 4.8. Assume that Assumptions 4.1, 4.2, and 4.3 all hold, and that
![]() $\Psi $
is
$\Psi $
is
![]() $\epsilon $
-monotonic. Then there exists a constant
$\epsilon $
-monotonic. Then there exists a constant
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $\alpha> 0$
and
$\alpha> 0$
and
![]() $\epsilon \in \{\pm 1\}$
, we have
$\epsilon \in \{\pm 1\}$
, we have
where
 $$ \begin{align*} \Sigma_{\alpha,-1}' &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{1 \leq x\leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(B(a,x)\cap E))),\\ \Sigma_\alpha" &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \log(1/\Psi^{-1}(\alpha^{-1} F(a^{-1}))),\\ \Sigma_{\alpha,1}' &{\, \stackrel{\mathrm{def}}{=}\, } \Sigma_{\alpha,-1}' + \Sigma_\alpha". \end{align*} $$
$$ \begin{align*} \Sigma_{\alpha,-1}' &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{1 \leq x\leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(B(a,x)\cap E))),\\ \Sigma_\alpha" &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \log(1/\Psi^{-1}(\alpha^{-1} F(a^{-1}))),\\ \Sigma_{\alpha,1}' &{\, \stackrel{\mathrm{def}}{=}\, } \Sigma_{\alpha,-1}' + \Sigma_\alpha". \end{align*} $$
Here
![]() $F(r) = r^\delta f(r^{-1})$
, where f is as in Assumption 4.1.
$F(r) = r^\delta f(r^{-1})$
, where f is as in Assumption 4.1.
Proof. Indeed,
 $$ \begin{align*} &\sum_{k = 1}^\infty \mu(J_{k,\alpha,\epsilon})\\ &\quad= \sum_{a\in E} \mu(a) \#\{k\in{\mathbb{N}} : \text{there exists } r \in [\|\phi_a'\|,1] r^{-\delta} \mu(B([a],r)) \lesseqgtr \alpha \Psi(\unicode{x3bb}^{-k} r)\}\\ &\quad= \sum_{a\in E} \mu(a) \max\{k\in{\mathbb{N}} : \text{there exists } r \in [\|\phi_a'\|,1] r^{-\delta} \mu(B([a],r)) \lesseqgtr \alpha \Psi(\unicode{x3bb}^{-k} r)\}\\ &\qquad(\text{since } \Psi \text{ is decreasing if } \epsilon=1 \text{ and increasing if } \epsilon=-1)\\ &\quad\asymp_{+,\times} \sum_{a\in E} \mu(a) \max(0,\max_{r \in [\|\phi_a'\|,1]} \log_\unicode{x3bb}(r/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))))\\ &\quad\in \bigg[\sum_{a\in E} \mu(a) \log_\unicode{x3bb}\|\phi_a'\|,C\bigg] + \sum_{a\in E} \mu(a) \max_{r \in [\|\phi_a'\|,1]} \log_\unicode{x3bb}(1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r))))\\ &\qquad(\text{since } r \leq 1 \lesssim 1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))). \end{align*} $$
$$ \begin{align*} &\sum_{k = 1}^\infty \mu(J_{k,\alpha,\epsilon})\\ &\quad= \sum_{a\in E} \mu(a) \#\{k\in{\mathbb{N}} : \text{there exists } r \in [\|\phi_a'\|,1] r^{-\delta} \mu(B([a],r)) \lesseqgtr \alpha \Psi(\unicode{x3bb}^{-k} r)\}\\ &\quad= \sum_{a\in E} \mu(a) \max\{k\in{\mathbb{N}} : \text{there exists } r \in [\|\phi_a'\|,1] r^{-\delta} \mu(B([a],r)) \lesseqgtr \alpha \Psi(\unicode{x3bb}^{-k} r)\}\\ &\qquad(\text{since } \Psi \text{ is decreasing if } \epsilon=1 \text{ and increasing if } \epsilon=-1)\\ &\quad\asymp_{+,\times} \sum_{a\in E} \mu(a) \max(0,\max_{r \in [\|\phi_a'\|,1]} \log_\unicode{x3bb}(r/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))))\\ &\quad\in \bigg[\sum_{a\in E} \mu(a) \log_\unicode{x3bb}\|\phi_a'\|,C\bigg] + \sum_{a\in E} \mu(a) \max_{r \in [\|\phi_a'\|,1]} \log_\unicode{x3bb}(1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r))))\\ &\qquad(\text{since } r \leq 1 \lesssim 1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))). \end{align*} $$
The first term is finite by Assumption 4.3. The second term can be analyzed by considering
 $$ \begin{align*} \Sigma_{1,\alpha} &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{a^{-1} \leq r \leq 1} \log_\unicode{x3bb}(1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))),\\ \Sigma_{2,\alpha} &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{\|\phi_a'\|\leq r \leq a^{-1}/3} \log_\unicode{x3bb}(1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))). \end{align*} $$
$$ \begin{align*} \Sigma_{1,\alpha} &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{a^{-1} \leq r \leq 1} \log_\unicode{x3bb}(1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))),\\ \Sigma_{2,\alpha} &{\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{\|\phi_a'\|\leq r \leq a^{-1}/3} \log_\unicode{x3bb}(1/\Psi^{-1}(\alpha^{-1} r^{-\delta} \mu(B([a],r)))). \end{align*} $$
Then
Now for
![]() $r> 0$
sufficiently small we have
$r> 0$
sufficiently small we have
 $$ \begin{align*} \mu(B(0,r)) &\geq \sum_{a\geq r^{-1}} \mu(a) \asymp \sum_{a\geq r^{-1}} a^{-2\delta} \\ &\asymp \sum_{k = 0}^\infty \#(E\cap [2^k r^{-1}, 2^{k+1} r^{-1}]) (2^k r^{-1})^{-2\delta} \\ &\asymp \sum_{k = 0}^\infty f(2^k r^{-1}) 2^{-2k\delta} r^{2\delta} \asymp f(r^{-1}) r^{2\delta}\\ &\quad\ \text{(since} f \text{ is regularly varying with exponent } s<2\delta) \end{align*} $$
$$ \begin{align*} \mu(B(0,r)) &\geq \sum_{a\geq r^{-1}} \mu(a) \asymp \sum_{a\geq r^{-1}} a^{-2\delta} \\ &\asymp \sum_{k = 0}^\infty \#(E\cap [2^k r^{-1}, 2^{k+1} r^{-1}]) (2^k r^{-1})^{-2\delta} \\ &\asymp \sum_{k = 0}^\infty f(2^k r^{-1}) 2^{-2k\delta} r^{2\delta} \asymp f(r^{-1}) r^{2\delta}\\ &\quad\ \text{(since} f \text{ is regularly varying with exponent } s<2\delta) \end{align*} $$
and similarly for the reverse direction, giving
When
![]() $r\geq a^{-1}$
, we have
$r\geq a^{-1}$
, we have
![]() $B(0,r)\cap [0,1] \subset B([a],r) \subset B(0,2r)$
, so
$B(0,r)\cap [0,1] \subset B([a],r) \subset B(0,2r)$
, so
and thus
![]() $\Sigma _{1,C^\epsilon \alpha }' \leq \Sigma _{1,\alpha } \leq \Sigma _{1,C^{-\epsilon } \alpha }'$
, where
$\Sigma _{1,C^\epsilon \alpha }' \leq \Sigma _{1,\alpha } \leq \Sigma _{1,C^{-\epsilon } \alpha }'$
, where
 $$ \begin{align*} \Sigma_{1,\alpha}' {\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{a^{-1} \leq r \leq 1} \log(1/\Psi^{-1}(\alpha^{-1} r^\delta f(r^{-1}))). \end{align*} $$
$$ \begin{align*} \Sigma_{1,\alpha}' {\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{a^{-1} \leq r \leq 1} \log(1/\Psi^{-1}(\alpha^{-1} r^\delta f(r^{-1}))). \end{align*} $$
Since f is regularly varying with exponent
![]() $s>\delta $
, the function
$s>\delta $
, the function
![]() $F(r) = r^\delta f(r^{-1})$
is monotonically decreasing for r sufficiently small, while
$F(r) = r^\delta f(r^{-1})$
is monotonically decreasing for r sufficiently small, while
![]() $\Psi ^{-1}$
is decreasing (respectively, increasing) if
$\Psi ^{-1}$
is decreasing (respectively, increasing) if
![]() $\epsilon =1$
(respectively,
$\epsilon =1$
(respectively,
![]() $\epsilon =-1$
). It follows that the maximum occurs at
$\epsilon =-1$
). It follows that the maximum occurs at
![]() $r = a^{-1}$
(respectively,
$r = a^{-1}$
(respectively,
![]() $r = 1$
), corresponding to
$r = 1$
), corresponding to
and
The latter series always converges, whereas the former series may either converge or diverge.
On the other hand, we have
Using the change of variables
![]() $r = a^{-2} x$
and the fact that
$r = a^{-2} x$
and the fact that
![]() $\mu (b) \asymp \mu (a) \asymp a^{-2\delta }$
for all
$\mu (b) \asymp \mu (a) \asymp a^{-2\delta }$
for all
![]() $b\in E$
such that
$b\in E$
such that
![]() $B([a],r)\cap [b]\neq \emptyset $
, we get
$B([a],r)\cap [b]\neq \emptyset $
, we get
![]() $\Sigma _{2,C^\epsilon \alpha }' \lesssim \Sigma _{2,\alpha } \lesssim \Sigma _{2,C^{-\epsilon }\alpha }'$
, where
$\Sigma _{2,C^\epsilon \alpha }' \lesssim \Sigma _{2,\alpha } \lesssim \Sigma _{2,C^{-\epsilon }\alpha }'$
, where
 $$ \begin{align} \Sigma_{2,\alpha}' {\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{1 \leq x\leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(B(a,x)\cap E))) \end{align} $$
$$ \begin{align} \Sigma_{2,\alpha}' {\, \stackrel{\mathrm{def}}{=}\, } \sum_{a\in E} \mu(a) \max_{1 \leq x\leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(B(a,x)\cap E))) \end{align} $$
and
![]() $C \geq 1$
is a constant. Combining (4.5), (4.6), and (4.7) yields the conclusion.
$C \geq 1$
is a constant. Combining (4.5), (4.6), and (4.7) yields the conclusion.
5. Proofs of main theorems
In this section we consider the Gauss IFS
![]() $\Phi _P$
, where P is the set of primes. We begin with a number-theoretic lemma.
$\Phi _P$
, where P is the set of primes. We begin with a number-theoretic lemma.
Lemma 5.1. For all
![]() $\delta < 1$
,
$\delta < 1$
,
where
![]() $f(N) = N/\log (N)$
is as in Assumption 4.1.
$f(N) = N/\log (N)$
is as in Assumption 4.1.
Proof. A well-known result of Hoheisel [Reference Hoheisel19] (see also [Reference Chandrasekharan6, Ch. V] for a book reference) states that there exists
![]() $\theta < 1$
such that
$\theta < 1$
such that
(This result has seen numerous improvements (see [Reference Pintz31] for a survey), but it does not matter very much for our purposes, although the lower bound does make a difference in our upper bound for the exact packing dimension. The most recent improvements we were aware of are
![]() $\theta = 6/11 + \epsilon $
for the upper bound [Reference Lou and Yao21] and
$\theta = 6/11 + \epsilon $
for the upper bound [Reference Lou and Yao21] and
![]() $\theta = 21/40$
for the lower bound [Reference Baker, Harman and Pintz1, pp. 562].)
$\theta = 21/40$
for the lower bound [Reference Baker, Harman and Pintz1, pp. 562].)
It follows that
In this case, since
![]() $\delta < 1$
and
$\delta < 1$
and
![]() $x \leq a$
we have
$x \leq a$
we have
 $$ \begin{align*} \frac{x}{\log(a)} = \frac{x}{a} f(a) \leq \bigg(\frac{x}{a}\bigg)^\delta f(a), \end{align*} $$
$$ \begin{align*} \frac{x}{\log(a)} = \frac{x}{a} f(a) \leq \bigg(\frac{x}{a}\bigg)^\delta f(a), \end{align*} $$
and combining yields (5.1) in this case. On the other hand, if
![]() $1 \leq x \leq a^\theta $
, then
$1 \leq x \leq a^\theta $
, then
since
demonstrating (5.1) for the second case.
Thus, for appropriate
![]() $C \geq 1$
,
$C \geq 1$
,
 $$ \begin{align*} \Sigma_{\alpha,-1}' &\leq \sum_{a\in P} \mu(a) \log(1/\Psi^{-1}(C\alpha^{-1} \max_{1 \leq x\leq a/3} x^{-\delta} (x/a)^\delta f(a)))\\ &= \sum_{a\in P} \mu(a) \log(1/\Psi^{-1}(C\alpha^{-1} a^{-\delta} f(a)))\\ &= \sum_{a\in P} \mu(a) \log(1/\Psi^{-1}(C\alpha^{-1} F(a^{-1}))) \asymp_+ \Sigma_{C^{-1}\alpha}". \end{align*} $$
$$ \begin{align*} \Sigma_{\alpha,-1}' &\leq \sum_{a\in P} \mu(a) \log(1/\Psi^{-1}(C\alpha^{-1} \max_{1 \leq x\leq a/3} x^{-\delta} (x/a)^\delta f(a)))\\ &= \sum_{a\in P} \mu(a) \log(1/\Psi^{-1}(C\alpha^{-1} a^{-\delta} f(a)))\\ &= \sum_{a\in P} \mu(a) \log(1/\Psi^{-1}(C\alpha^{-1} F(a^{-1}))) \asymp_+ \Sigma_{C^{-1}\alpha}". \end{align*} $$
It follows that
![]() $\Sigma _{\alpha ,1}' \lesssim \Sigma _{C^{-1}\alpha }"$
.
$\Sigma _{\alpha ,1}' \lesssim \Sigma _{C^{-1}\alpha }"$
.
Proof of Theorem 2.1
Set
![]() $\epsilon {\kern-1pt}={\kern-1pt}1$
and
$\epsilon {\kern-1pt}={\kern-1pt}1$
and
![]() $E {\kern-1pt}={\kern-1pt} P$
. If
$E {\kern-1pt}={\kern-1pt} P$
. If
![]() $\Psi $
is increasing, then
$\Psi $
is increasing, then
![]() $\mathcal H^\psi (\mu ) {\kern-1pt}\lesssim{\kern-1pt} \mathcal H^\delta (\mu ) = 0$
and the series (2.1) diverges, so we may henceforth assume that
$\mathcal H^\psi (\mu ) {\kern-1pt}\lesssim{\kern-1pt} \mathcal H^\delta (\mu ) = 0$
and the series (2.1) diverges, so we may henceforth assume that
![]() $\Psi $
is decreasing, allowing us to use Lemma 4.8. Using the Iverson bracket notation
$\Psi $
is decreasing, allowing us to use Lemma 4.8. Using the Iverson bracket notation
 $$ \begin{align*}[\Phi] = \left\{\begin{matrix}1, & \Phi\ \text{true},\\0, &\,\Phi\ \text{false},\end{matrix}\right.\end{align*} $$
$$ \begin{align*}[\Phi] = \left\{\begin{matrix}1, & \Phi\ \text{true},\\0, &\,\Phi\ \text{false},\end{matrix}\right.\end{align*} $$
we have
 $$ \begin{align*} \Sigma_\alpha" &\asymp_+ \sum_{a \in P} \mu(a) \sum_{k=1}^\infty [ k \leq \log_\unicode{x3bb} ( 1/\Psi^{-1}(\alpha^{-1} F(a^{-1}) ) ]\\ &= \sum_{a\in P} \mu(a) \sum_{k=1}^\infty [F^{-1}(\alpha\Psi(\unicode{x3bb}^{-k})) \geq a^{-1}]\\ &\asymp \sum_{k=1}^\infty \sum_{\substack{a\in P \\ a \geq 1/F^{-1}(\alpha\Psi(\unicode{x3bb}^{-k}))}} a^{-2\delta}\\ &\asymp \sum_{k=1}^\infty \frac{x^{1-2\delta}}{\log x}\upharpoonleft_{x=1/F^{-1}(\alpha\Psi(\unicode{x3bb}^{-k}))} \end{align*} $$
$$ \begin{align*} \Sigma_\alpha" &\asymp_+ \sum_{a \in P} \mu(a) \sum_{k=1}^\infty [ k \leq \log_\unicode{x3bb} ( 1/\Psi^{-1}(\alpha^{-1} F(a^{-1}) ) ]\\ &= \sum_{a\in P} \mu(a) \sum_{k=1}^\infty [F^{-1}(\alpha\Psi(\unicode{x3bb}^{-k})) \geq a^{-1}]\\ &\asymp \sum_{k=1}^\infty \sum_{\substack{a\in P \\ a \geq 1/F^{-1}(\alpha\Psi(\unicode{x3bb}^{-k}))}} a^{-2\delta}\\ &\asymp \sum_{k=1}^\infty \frac{x^{1-2\delta}}{\log x}\upharpoonleft_{x=1/F^{-1}(\alpha\Psi(\unicode{x3bb}^{-k}))} \end{align*} $$
Now we have
![]() $f(x) {\kern-1pt}={\kern-1pt} x/\log x$
, thus
$f(x) {\kern-1pt}={\kern-1pt} x/\log x$
, thus
![]() $F(r) {\kern-1pt}={\kern-1pt} r^{\delta -1} / \log (r^{-1})$
and
$F(r) {\kern-1pt}={\kern-1pt} r^{\delta -1} / \log (r^{-1})$
and
![]() $F^{-1}(x){\kern-1pt} \asymp{\kern-1pt} (x\log x)^{1/(\delta -1)}$
. So we can continue the computation as
$F^{-1}(x){\kern-1pt} \asymp{\kern-1pt} (x\log x)^{1/(\delta -1)}$
. So we can continue the computation as
 $$ \begin{align*} &\asymp \sum_{k=1}^\infty \frac{x^{1-2\delta}}{\log x}\upharpoonleft_{x=(y\log y)^{1/(1-\delta)}, y=\alpha\Psi(\unicode{x3bb}^{-k})}\\ &\asymp \sum_{k=1}^\infty \frac{(y\log y)^{({1-2\delta})/({1-\delta})}}{\log y}\upharpoonleft_{y=\alpha\Psi(\unicode{x3bb}^{-k})}\\ &\asymp \sum_{k=1}^\infty \frac{(y\log y)^{({1-2\delta})/({1-\delta})}}{\log y}\upharpoonleft_{y=\Psi(\unicode{x3bb}^{-k})}. \end{align*} $$
$$ \begin{align*} &\asymp \sum_{k=1}^\infty \frac{x^{1-2\delta}}{\log x}\upharpoonleft_{x=(y\log y)^{1/(1-\delta)}, y=\alpha\Psi(\unicode{x3bb}^{-k})}\\ &\asymp \sum_{k=1}^\infty \frac{(y\log y)^{({1-2\delta})/({1-\delta})}}{\log y}\upharpoonleft_{y=\alpha\Psi(\unicode{x3bb}^{-k})}\\ &\asymp \sum_{k=1}^\infty \frac{(y\log y)^{({1-2\delta})/({1-\delta})}}{\log y}\upharpoonleft_{y=\Psi(\unicode{x3bb}^{-k})}. \end{align*} $$
If this series converges for all
![]() $\alpha> 0$
, then so do
$\alpha> 0$
, then so do
![]() $\Sigma _{\alpha ,1}'$
and (by Lemma 4.8)
$\Sigma _{\alpha ,1}'$
and (by Lemma 4.8)
![]() $\sum _k \mu (J_{k,\alpha ,1})$
, and thus by Lemma 4.7 we have
$\sum _k \mu (J_{k,\alpha ,1})$
, and thus by Lemma 4.7 we have
![]() $\mathcal H^\psi (\mu )=\infty $
. On the other hand, if the series diverges, then so does
$\mathcal H^\psi (\mu )=\infty $
. On the other hand, if the series diverges, then so does
![]() $\sum _k \mu (J_{k,\alpha ,1})$
for all
$\sum _k \mu (J_{k,\alpha ,1})$
for all
![]() $\alpha> 0$
, and thus by Lemma 4.7 we have
$\alpha> 0$
, and thus by Lemma 4.7 we have
![]() $\mathcal H^\psi (\mu )=0$
.
$\mathcal H^\psi (\mu )=0$
.
Proof of Theorem 2.3
We can get bounds on the exact packing dimension of
![]() $\mu _P$
by using known results about the distribution of primes. First, we state the strongest known lower bound on two-sided gaps.
$\mu _P$
by using known results about the distribution of primes. First, we state the strongest known lower bound on two-sided gaps.
Theorem 5.2. [Reference Maier22]
Let
![]() $p_n$
denote the nth prime and let
$p_n$
denote the nth prime and let
![]() $d_n = p_{n+1} - p_n$
. For all k,
$d_n = p_{n+1} - p_n$
. For all k,
where
![]() $\phi $
is as in (2.2).
$\phi $
is as in (2.2).
Let
![]() $k = 2$
and let
$k = 2$
and let
![]() $(n_\ell )$
be a sequence along which the limit superior is achieved, and let
$(n_\ell )$
be a sequence along which the limit superior is achieved, and let
![]() $a_\ell = p_{n_\ell + 2}\in P$
for some
$a_\ell = p_{n_\ell + 2}\in P$
for some
![]() $\ell \in {\mathbb {N}}$
, so that
$\ell \in {\mathbb {N}}$
, so that
![]() $P\cap B(a_\ell ,x) = \{a_\ell \}$
, where
$P\cap B(a_\ell ,x) = \{a_\ell \}$
, where
![]() $x = c\phi (a_\ell )$
for some constant
$x = c\phi (a_\ell )$
for some constant
![]() $c>0$
. Then we have
$c>0$
. Then we have
 $$ \begin{align*} \Sigma_{\alpha,-1}' &\gtrsim \sum_{a\in P} a^{-2\delta} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(P\cap B(a,x))))\\ &\geq \sum_{\ell\in{\mathbb{N}}} a_\ell^{-2\delta} \log(1/\Psi^{-1}(\alpha^{-1} c^{-\delta}\phi(a_\ell)^{-\delta} )). \end{align*} $$
$$ \begin{align*} \Sigma_{\alpha,-1}' &\gtrsim \sum_{a\in P} a^{-2\delta} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(P\cap B(a,x))))\\ &\geq \sum_{\ell\in{\mathbb{N}}} a_\ell^{-2\delta} \log(1/\Psi^{-1}(\alpha^{-1} c^{-\delta}\phi(a_\ell)^{-\delta} )). \end{align*} $$
Let
![]() $\psi (r) = r^\delta \phi ^{-\delta }(\log (1/r))$
as in (2.3), so that
$\psi (r) = r^\delta \phi ^{-\delta }(\log (1/r))$
as in (2.3), so that
![]() $\Psi (r) = \phi ^{-\delta }(\log (1/r))$
and
$\Psi (r) = \phi ^{-\delta }(\log (1/r))$
and
![]() $\Psi ^{-1}(x) = \exp (-\phi ^{-1}(x^{-1/\delta }))$
. Note that
$\Psi ^{-1}(x) = \exp (-\phi ^{-1}(x^{-1/\delta }))$
. Note that
 $$ \begin{align*} \phi^{-1}(x) = \log(1/\Psi^{-1}(x^{-\delta})) \asymp e^x \frac{\log^2 x}{x \log\log x}, \end{align*} $$
$$ \begin{align*} \phi^{-1}(x) = \log(1/\Psi^{-1}(x^{-\delta})) \asymp e^x \frac{\log^2 x}{x \log\log x}, \end{align*} $$
and thus, letting
![]() $\alpha = c^{-\delta }\gamma ^{-\delta }$
,
$\alpha = c^{-\delta }\gamma ^{-\delta }$
,
 $$ \begin{align*} a^{-2\delta} \log(1/\Psi^{-1}(\alpha^{-1} c^{-\delta}\phi(a)^{-\delta} )) &= a^{-2\delta} \phi^{-1}(\gamma \phi(a))\\ &\asymp a^{-2\delta} a^\gamma \end{align*} $$
$$ \begin{align*} a^{-2\delta} \log(1/\Psi^{-1}(\alpha^{-1} c^{-\delta}\phi(a)^{-\delta} )) &= a^{-2\delta} \phi^{-1}(\gamma \phi(a))\\ &\asymp a^{-2\delta} a^\gamma \end{align*} $$
so that
![]() $\Sigma _{\alpha ,-1}'$
diverges for
$\Sigma _{\alpha ,-1}'$
diverges for
![]() $\gamma{\kern-1.5pt}>{\kern-1.5pt} 2\delta $
. Combining with Lemmas 4.7 and 4.8 demonstrates (2.3).
$\gamma{\kern-1.5pt}>{\kern-1.5pt} 2\delta $
. Combining with Lemmas 4.7 and 4.8 demonstrates (2.3).
On the other hand, we use the lower bound of Hoheisel’s theorem (5.2) to get an upper bound on the exact packing dimension. Let
![]() $\theta = 21/40$
. Fix
$\theta = 21/40$
. Fix
![]() $a\in P$
and
$a\in P$
and
![]() $1 \leq x \leq a/3$
, and let
$1 \leq x \leq a/3$
, and let
![]() $\theta = 21/40$
as in (5.1). If
$\theta = 21/40$
as in (5.1). If
![]() $x \geq a^\theta $
, then we have
$x \geq a^\theta $
, then we have
 $$ \begin{align*} x^{-\delta} \#(P\cap B(a,x)) \gtrsim x^{-\delta} \frac{x}{\log(a)} \geq a^{-\theta\delta} \frac{a^\theta}{\log(a)} \gtrsim a^{-\theta\delta}, \end{align*} $$
$$ \begin{align*} x^{-\delta} \#(P\cap B(a,x)) \gtrsim x^{-\delta} \frac{x}{\log(a)} \geq a^{-\theta\delta} \frac{a^\theta}{\log(a)} \gtrsim a^{-\theta\delta}, \end{align*} $$
and if
![]() $x \leq a^\theta $
, then we have
$x \leq a^\theta $
, then we have
Thus, for appropriate
![]() $c_2> 0$
,
$c_2> 0$
,
 $$ \begin{align*} \Sigma_{\alpha,-1}' &\asymp \sum_{a\in P} a^{-2\delta} \max_{1 \leq x \leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(P\cap B(a,x))))\\ &\leq \sum_{a\in P} a^{-2\delta} \log(1/\Psi^{-1}(c_2 \alpha^{-1} a^{-\theta\delta})). \end{align*} $$
$$ \begin{align*} \Sigma_{\alpha,-1}' &\asymp \sum_{a\in P} a^{-2\delta} \max_{1 \leq x \leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(P\cap B(a,x))))\\ &\leq \sum_{a\in P} a^{-2\delta} \log(1/\Psi^{-1}(c_2 \alpha^{-1} a^{-\theta\delta})). \end{align*} $$
Letting
we get
Proof of Theorem 2.5
In what follows we assume the cases
![]() $k=1,2$
of Conjecture 2.4. From the case
$k=1,2$
of Conjecture 2.4. From the case
![]() $k=1$
of Conjecture 2.4, in particular from
$k=1$
of Conjecture 2.4, in particular from
![]() $R_1 < \infty $
, it follows that the gaps between primes have size
$R_1 < \infty $
, it follows that the gaps between primes have size
![]() $d_n = O(\log ^2(p_n))$
, and thus for all
$d_n = O(\log ^2(p_n))$
, and thus for all
![]() $a\in P$
and
$a\in P$
and
![]() $1\leq x\leq a/3$
, we have
$1\leq x\leq a/3$
, we have
 $$ \begin{align} x^{-\delta} \#(P\cap B(a,x)) \gtrsim x^{-\delta}\bigg( \frac{x}{\log^2(a)} + 1\bigg) \geq x^{-\delta}\bigg(\frac{x}{\log^2(a)}\bigg)^\delta = \frac{1}{\log^{2\delta}(a)}\cdot \end{align} $$
$$ \begin{align} x^{-\delta} \#(P\cap B(a,x)) \gtrsim x^{-\delta}\bigg( \frac{x}{\log^2(a)} + 1\bigg) \geq x^{-\delta}\bigg(\frac{x}{\log^2(a)}\bigg)^\delta = \frac{1}{\log^{2\delta}(a)}\cdot \end{align} $$
On the other hand, from the case
![]() $k=2$
, in particular
$k=2$
, in particular
![]() $R_2> 0$
, it follows that for an appropriate constant
$R_2> 0$
, it follows that for an appropriate constant
![]() $c> 0$
there exists an infinite set
$c> 0$
there exists an infinite set
![]() $I \subset P$
(that is, the set
$I \subset P$
(that is, the set
![]() $\{p_{n+2} : \min (d_{n+1},d_{n+2}) \geq c\log ^2(p_{n+2})\}$
for an appropriate constant
$\{p_{n+2} : \min (d_{n+1},d_{n+2}) \geq c\log ^2(p_{n+2})\}$
for an appropriate constant
![]() $c> 0$
) such that for all
$c> 0$
) such that for all
![]() $a\in I$
and
$a\in I$
and
![]() $1\leq x = x_a = c\log ^2(a) \leq a/3$
we have
$1\leq x = x_a = c\log ^2(a) \leq a/3$
we have
![]() $P\cap B(a,x) = \{a\}$
and thus
$P\cap B(a,x) = \{a\}$
and thus
 $$ \begin{align} x^{-\delta} \#(P\cap B(a,x)) = x^{-\delta} \asymp \frac{1}{\log^{2\delta}(a)}. \end{align} $$
$$ \begin{align} x^{-\delta} \#(P\cap B(a,x)) = x^{-\delta} \asymp \frac{1}{\log^{2\delta}(a)}. \end{align} $$
Now let
![]() $\psi (r) = r^\delta \log ^{-2\delta }\log (1/r)$
be as in (2.5), so that
$\psi (r) = r^\delta \log ^{-2\delta }\log (1/r)$
be as in (2.5), so that
![]() $\Psi (r) = \log ^{-2\delta }(1/r)$
and
$\Psi (r) = \log ^{-2\delta }(1/r)$
and
![]() $\Psi ^{-1}(x) = \exp (-\exp (x^{-1/2\delta }))$
. In particular,
$\Psi ^{-1}(x) = \exp (-\exp (x^{-1/2\delta }))$
. In particular,
![]() $\Psi ^{-1}$
is increasing. It follows that for appropriate
$\Psi ^{-1}$
is increasing. It follows that for appropriate
![]() $C_1 \geq 1 \geq C_2> 0$
,
$C_1 \geq 1 \geq C_2> 0$
,
 $$ \begin{align*} [a\in I]\log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_1}{\log^{2\delta}(a)}\bigg)\bigg) &\underset{(5.4)}{\leq} \max_{1\leq x\leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(B(a,x)\cap P)))\\ &\underset{(5.3)}{\leq} \log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_2}{\log^{2\delta}(a)}\bigg)\bigg), \end{align*} $$
$$ \begin{align*} [a\in I]\log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_1}{\log^{2\delta}(a)}\bigg)\bigg) &\underset{(5.4)}{\leq} \max_{1\leq x\leq a/3} \log(1/\Psi^{-1}(\alpha^{-1} x^{-\delta} \#(B(a,x)\cap P)))\\ &\underset{(5.3)}{\leq} \log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_2}{\log^{2\delta}(a)}\bigg)\bigg), \end{align*} $$
and plugging into (4.7) yields
 $$ \begin{align*} \sum_{a\in I} \mu(a) \log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_1}{\log^{2\delta}(a)}\bigg)\bigg) \leq \Sigma_{\alpha,-1}' \leq \sum_{a\in P} \mu(a) \log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_2}{\log^{2\delta}(a)}\bigg)\bigg). \end{align*} $$
$$ \begin{align*} \sum_{a\in I} \mu(a) \log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_1}{\log^{2\delta}(a)}\bigg)\bigg) \leq \Sigma_{\alpha,-1}' \leq \sum_{a\in P} \mu(a) \log\bigg(1/\Psi^{-1}\bigg(\alpha^{-1} \frac{C_2}{\log^{2\delta}(a)}\bigg)\bigg). \end{align*} $$
We get
 $$ \begin{align*} \sum_{a\in I} a^{-2\delta} a^{(\alpha C_1^{-1})^{1/2\delta}} \lesssim \Sigma_{\alpha,-1}' \lesssim \sum_{a\in P} a^{-2\delta} a^{(\alpha C_2^{-1})^{1/2\delta}}. \end{align*} $$
$$ \begin{align*} \sum_{a\in I} a^{-2\delta} a^{(\alpha C_1^{-1})^{1/2\delta}} \lesssim \Sigma_{\alpha,-1}' \lesssim \sum_{a\in P} a^{-2\delta} a^{(\alpha C_2^{-1})^{1/2\delta}}. \end{align*} $$
By choosing
![]() $\alpha> 0$
so that
$\alpha> 0$
so that
![]() $(\alpha C_2^{-1})^{1/2\delta } < 2\delta - 1$
, we get
$(\alpha C_2^{-1})^{1/2\delta } < 2\delta - 1$
, we get
![]() $\Sigma _{\alpha ,-1}' < \infty $
, and by choosing
$\Sigma _{\alpha ,-1}' < \infty $
, and by choosing
![]() $\alpha> 0$
so that
$\alpha> 0$
so that
![]() $(\alpha C_1^{-1})^{1/2\delta }> 2\delta $
, we get
$(\alpha C_1^{-1})^{1/2\delta }> 2\delta $
, we get
![]() $\Sigma _{\alpha ,-1}' = \infty $
. It follows then from Lemmas 4.7 and 4.8 that
$\Sigma _{\alpha ,-1}' = \infty $
. It follows then from Lemmas 4.7 and 4.8 that
![]() $\mathcal P^\psi (\mu )$
is positive and finite.
$\mathcal P^\psi (\mu )$
is positive and finite.
Acknowledgements
We dedicate this paper to our friend, collaborator, and teacher, Mariusz Urbański, on the occasion of his being awarded the 2023 Sierpiński Medal. The second-named author was supported by a Royal Society University Research Fellowship URF∖R1∖180649. We thank the referees for carefully checking the paper and making suggestions to improve the exposition.