Article contents
Ergodic theorem in CAT(0) spaces in terms of inductive means
Published online by Cambridge University Press: 17 March 2022
Abstract
Let 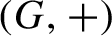 $(G,+)$ be a compact, abelian, and metrizable topological group. In this group we take
$(G,+)$ be a compact, abelian, and metrizable topological group. In this group we take 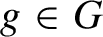 $g\in G$ such that the corresponding automorphism
$g\in G$ such that the corresponding automorphism 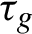 $\tau _g$ is ergodic. The main result of this paper is a new ergodic theorem for functions in
$\tau _g$ is ergodic. The main result of this paper is a new ergodic theorem for functions in 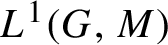 $L^1(G,M)$, where M is a Hadamard space. The novelty of our result is that we use inductive means to average the elements of the orbit
$L^1(G,M)$, where M is a Hadamard space. The novelty of our result is that we use inductive means to average the elements of the orbit 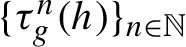 $\{\tau _g^n(h)\}_{n\in \mathbb {N}}$. The advantage of inductive means is that they can be explicitly computed in many important examples. The proof of the ergodic theorem is done firstly for continuous functions, and then it is extended to
$\{\tau _g^n(h)\}_{n\in \mathbb {N}}$. The advantage of inductive means is that they can be explicitly computed in many important examples. The proof of the ergodic theorem is done firstly for continuous functions, and then it is extended to 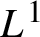 $L^1$ functions. The extension is based on a new construction of mollifiers in Hadamard spaces. This construction has the advantage that it only uses the metric structure and the existence of barycenters, and does not require the existence of an underlying vector space. For this reason, it can be used in any Hadamard space, in contrast to those results that need to use the tangent space or some chart to define the mollifier.
$L^1$ functions. The extension is based on a new construction of mollifiers in Hadamard spaces. This construction has the advantage that it only uses the metric structure and the existence of barycenters, and does not require the existence of an underlying vector space. For this reason, it can be used in any Hadamard space, in contrast to those results that need to use the tangent space or some chart to define the mollifier.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 3
- Cited by


