Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T09:49:37.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant wrapped Floer homology and symmetric periodic Reeb orbits

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems Smooth dynamical systems: general theory Symplectic geometry, contact geometry

Published online by Cambridge University Press:  04 February 2021

JOONTAE KIM ,
SEONGCHAN KIM  and
MYEONGGI KWON
JOONTAE KIM*
Affiliation:
School of Mathematics, Korea Institute for Advanced Study, 85 Hoegiro, Dongdaemun-gu, Seoul 02455, Republic of Korea (e-mail: joontae@kias.re.kr)
SEONGCHAN KIM
Affiliation:
Institut de Mathématiques, Université de Neuchâtel, Rue Emile-Argand 11, 2000 Neuchâtel, Switzerland (e-mail: seongchan.kim@unine.ch)
MYEONGGI KWON
Affiliation:
Center for Geometry and Physics, Institute for Basic Science (IBS), Pohang 37673, Korea (e-mail: mkwon@ibs.re.kr)
*
e-mail: joontae@kias.re.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this article is to apply a Floer theory to study symmetric periodic Reeb orbits. We define positive equivariant wrapped Floer homology using a (anti-)symplectic involution on a Liouville domain and investigate its algebraic properties. By a careful analysis of index iterations, we obtain a non-trivial lower bound on the minimal number of geometrically distinct symmetric periodic Reeb orbits on a certain class of real contact manifolds. This includes non-degenerate real dynamically convex star-shaped hypersurfaces in 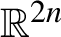${\mathbb {R}}^{2n}$ which are invariant under complex conjugation. As a result, we give a partial answer to the Seifert conjecture on brake orbits in the contact setting.

Keywords

equivariant wrapped Floer homologysymmetric periodic Reeb orbitSeifert conjecturebrake orbit

MSC classification

Primary: 53D40: Floer homology and cohomology, symplectic aspects 37C27: Periodic orbits of vector fields and flows
Secondary: 37J05: General theory, relations with symplectic geometry and topology

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 5 , May 2022 , pp. 1708 - 1763
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abouzaid, M. and Seidel, P.. An open string analogue of Viterbo functoriality. Geom. Topol. 14(2) (2010), 627–718.CrossRefGoogle Scholar
Albers, P. and Frauenfelder, U.. Leaf-wise intersections and Rabinowitz Floer homology. J. Topol. Anal. 2(1) (2010), 77–98.CrossRefGoogle Scholar
Ambrosetti, A., Benci, V. and Long, Y.. A note on the existence of multiple brake orbits. Nonlinear Anal. 21(9) (1993), 643–649.CrossRefGoogle Scholar
Benci, V.. Closed geodesics for the Jacobi metric and periodic solutions of prescribed energy of natural Hamiltonian systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(5) (1984), 401–412.CrossRefGoogle Scholar
Bolotin, S. V.. Libration motions of natural dynamical systems. Vestnik Moskov. Univ. Ser. I Mat. Mekh. (6) (1978), 72–77.Google Scholar
Bourgeois, F. and Oancea, A.. Symplectic homology, autonomous Hamiltonians, and Morse–Bott moduli spaces. Duke Math. J. 146(1) (2009), 71–174.CrossRefGoogle Scholar
Bourgeois, F. and Oancea, A.. ${S}^1$ -equivariant symplectic homology and linearized contact homology. Int. Math. Res. Not. 2017(13) (2017), 3849–3937.Google Scholar
Duistermaat, J. J.. On the Morse index in variational calculus. Adv. Math. 21(1976), 173–195.CrossRefGoogle Scholar
Floer, A., Hofer, H. and Salamon, D.. Transversality in elliptic Morse theory for the symplectic action. Duke Math. J. 80(1) (1995), 251–292.CrossRefGoogle Scholar
Frauenfelder, U.. Dihedral homology and the moon. J. Fixed Point Theory Appl. 14(1) (2013), 55–69.CrossRefGoogle Scholar
Frauenfelder, U. and Kang, J.. Real holomorphic curves and invariant global surfaces of section. Proc. Lond. Math. Soc. (3) 112(3) (2016), 477–511.CrossRefGoogle Scholar
Frauenfelder, U. and van Koert, O.. The Hörmander index of symmetric periodic orbits. Geom. Dedicata 168(2014), 197–205.CrossRefGoogle Scholar
Frauenfelder, U. and van Koert, O.. The Restricted Three Body Problem and Holomorphic Curves (Pathways in Mathematics), 1st edn. Birkhäuser, Basel, 2018.CrossRefGoogle Scholar
Giambò, R., Giannoni, F. and Piccione, P.. Multiple brake orbits in $m$ -dimensional disks. Calc. Var. Partial Differential Equations 54(3) (2015), 2553–2580.CrossRefGoogle Scholar
Giambò, R., Giannoni, F. and Picione, P.. Multiple brake orbits and homoclinics in Riemannian manifolds. Arch. Ration. Mech. Anal. 200(2) (2011), 691–724.CrossRefGoogle Scholar
Giambò, R., Giannoni, F. and Picione, P.. Examples with minimal number of brake orbits and homoclinics in annular potential regions. J. Differential Equations 256(8) (2014), 2677–2690.CrossRefGoogle Scholar
Gutt, J.. The positive equivariant symplectic homology as an invariant for some contact manifolds. J. Symplectic Geom. 15(4) (2017), 1019–1069.CrossRefGoogle Scholar
Gutt, J. and Kang, J.. On the minimal number of periodic orbits on some hypersurfaces in ${\mathbb{R}}^{2n}$ . Ann. Inst. Fourier (Grenoble) 66(6) (2016), 2485–2505.CrossRefGoogle Scholar
Hayashi, K.. Periodic solution of classical Hamiltonian systems. Tokyo. J. Math. 6(2) (1983), 473–486.CrossRefGoogle Scholar
Hofer, H., Wysocki, K. and Zehnder, E.. The dynamics on three-dimensional strictly convex energy surfaces. Ann. of Math. 148(1) (1998), 197–289.CrossRefGoogle Scholar
Hörmander, L.. Fourier integral operators. I. Acta Math. 127(1–2) (1971), 79–183.CrossRefGoogle Scholar
Hutchings, M.. Floer homology of families. I. Algebr. Geom. Topol. 8(1) (2008), 435–492.CrossRefGoogle Scholar
Kang, J.. Symplectic homology of displaceable Liouville domains and leafwise intersection points. Geom. Dedicata 170(1) (2014), 135–142.CrossRefGoogle Scholar
Kang, J.. On reversible maps and symmetric periodic points. Ergod. Th. & Dynam. Sys. 38(4) (2018), 1479–1498.CrossRefGoogle Scholar
Kato, T.. Perturbation Theory for Linear Operators. Grundlehren der Mathematischen Wissenschaften, Band 132, 2nd edn. Springer, Berlin, 1976.Google Scholar
Kim, J., Kwon, M. and Lee, J.. Volume growth in the component of fibered twists. Commun. Contemp. Math. 20(8) (2018), 1850014, 43.CrossRefGoogle Scholar
Kwon, M. and van Koert, O.. Brieskorn manifolds in contact topology. Bull. Lond. Math. Soc. 48(2) (2016), 173–241.CrossRefGoogle Scholar
Liu, C. and Zhang, D.. Multiplicity of brake orbits on compact convex symmetric reversible hypersurfaces in ${\mathbb{R}}^{2n}$ . Proc. Lond. Math. Soc. 107(3) (2013), 1–38.Google Scholar
Liu, C. and Zhang, D.. Iteration theory of $l$ -index and multiplicity of brake orbits. J. Differential Equations 257(4) (2014), 1194–1245.CrossRefGoogle Scholar
Liu, C. and Zhang, D.. Multiple brake orbits on compact convex symmetric reversible hypersurfaces in ${\mathbb{R}}^{2n}$ . Ann. Inst. H. Poincaré Anal. Non Linéaire 31(3) (2014), 531–554.Google Scholar
Liu, C. and Zhang, D.. Seifert conjecture in the even convex case. Comm. Pure Appl. Math. 67(10) (2014), 1563–1604.CrossRefGoogle Scholar
Long, Y.. Bott formula of the Maslov-type index theory. Pacific J. Math. 187(1) (1999), 113–149.CrossRefGoogle Scholar
Long, Y., Zhang, D. and Zhu, C.. Multiple brake orbits in bounded symmetric domains. Adv. Math. 203(2) (2006), 568–635.CrossRefGoogle Scholar
McDuff, D. and Salamon, D.. Introduction to Symplectic Topology (Oxford Graduate Texts in Mathematics), 3rd edn. Oxford University Press, Oxford, 2017.CrossRefGoogle Scholar
Merry, W. J.. Lagrangian Rabinowitz Floer homology and twisted cotangent bundles. Geom. Dedicata 171(1) (2014), 345–386.CrossRefGoogle Scholar
Mohnke, K.. Holomorphic disks and the chord conjecture. Ann. of Math. (2) 154(1) (2001), 219–222.CrossRefGoogle Scholar
Poźniak, M.. Floer homology, Novikov rings and clean intersections. Northern California Symplectic Geometry Seminar (American Mathematical Society Translations Series 2, 196). American Mathematical Society, Providence, RI, 1999, pp. 119–181.Google Scholar
Rabinowitz, P. H.. On the existence of periodic solutions for a class of symmetric Hamiltonian systems. Nonlinear Anal. 11(5) (1987), 599–611.CrossRefGoogle Scholar
Ritter, A. F.. Topological quantum field theory structure on symplectic cohomology. J. Topol. 6(2) (2013), 391–489.CrossRefGoogle Scholar
Robbin, J. and Salamon, D.. The Maslov index for paths. Topology 32(4) (1993), 827–844.CrossRefGoogle Scholar
Robbin, J. and Salamon, D.. The spectral flow and the Maslov index. Bull. Lond. Math. Soc. 27(1) (1995), 1–33.CrossRefGoogle Scholar
Salamon, D. and Zehnder, E.. Morse theory for periodic solutions of Hamiltonian systems and the Maslov index. Comm. Pure Appl. Math. 45(10) (1992), 1303–1360.CrossRefGoogle Scholar
Seidel, P. and Smith, I.. Localization for involutions in Floer cohomology. Geom. Funct. Anal. 20(6) (2010), 1464–1501.CrossRefGoogle Scholar
Seifert, H.. Periodische Bewegungen Mechanischer Systeme. Math. Z. 51 (1948), 197–216.CrossRefGoogle Scholar
Szulkin, A.. An index theory and existence of multiple brake orbits for star-shaped Hamiltonian systems. Math. Ann. 283(2) (1989), 241–255.CrossRefGoogle Scholar
van Groesen, E.. Analytical mini-max methods for Hamiltonian brake orbits of prescribed energy. J. Math. Anal. Appl. 132(1) (1988), 1–12.CrossRefGoogle Scholar
Viterbo, C.. Functors and computations in Floer homology with applications. I. Geom. Funct. Anal. 9(5) (1999), 985–1033.CrossRefGoogle Scholar
Zhang, D.. Brake type closed characteristics on reversible compact convex hypersurfaces in ${\mathbb{R}}^{2n}$ . Nonlinear Anal. 74 (2011), 3149–3158.CrossRefGoogle Scholar