Article contents
Equidistribution of Farey sequences on horospheres in covers of 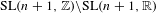 $\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
$\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
Published online by Cambridge University Press: 07 October 2019
Abstract
We establish the limiting distribution of certain subsets of Farey sequences, i.e., sequences of primitive rational points, on expanding horospheres in covers  $\unicode[STIX]{x1D6E5}\backslash \text{SL}(n+1,\mathbb{R})$ of
$\unicode[STIX]{x1D6E5}\backslash \text{SL}(n+1,\mathbb{R})$ of  $\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ , where
$\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ , where 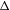 $\unicode[STIX]{x1D6E5}$ is a finite-index subgroup of
$\unicode[STIX]{x1D6E5}$ is a finite-index subgroup of 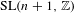 $\text{SL}(n+1,\mathbb{Z})$ . These subsets can be obtained by projecting to the hyperplane
$\text{SL}(n+1,\mathbb{Z})$ . These subsets can be obtained by projecting to the hyperplane 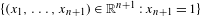 $\{(x_{1},\ldots ,x_{n+1})\in \mathbb{R}^{n+1}:x_{n+1}=1\}$ sets of the form
$\{(x_{1},\ldots ,x_{n+1})\in \mathbb{R}^{n+1}:x_{n+1}=1\}$ sets of the form 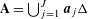 $\mathbf{A}=\bigcup _{j=1}^{J}\mathbf{a}_{j}\unicode[STIX]{x1D6E5}$ , where for all
$\mathbf{A}=\bigcup _{j=1}^{J}\mathbf{a}_{j}\unicode[STIX]{x1D6E5}$ , where for all 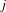 $j$ ,
$j$ , 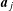 $\mathbf{a}_{j}$ is a primitive lattice point in
$\mathbf{a}_{j}$ is a primitive lattice point in 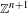 $\mathbb{Z}^{n+1}$ . Our method involves applying the equidistribution of expanding horospheres in quotients of
$\mathbb{Z}^{n+1}$ . Our method involves applying the equidistribution of expanding horospheres in quotients of 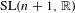 $\text{SL}(n+1,\mathbb{R})$ developed by Marklof and Strömbergsson, and more precisely understanding how the full Farey sequence distributes in
$\text{SL}(n+1,\mathbb{R})$ developed by Marklof and Strömbergsson, and more precisely understanding how the full Farey sequence distributes in 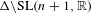 $\unicode[STIX]{x1D6E5}\backslash \text{SL}(n+1,\mathbb{R})$ when embedded on expanding horospheres as done in previous work by Marklof. For each of the Farey sequence subsets, we extend the statistical results by Marklof regarding the full multidimensional Farey sequences, and solutions by Athreya and Ghosh to Diophantine approximation problems of Erdős–Szüsz–Turán and Kesten. We also prove that Marklof’s result on the asymptotic distribution of Frobenius numbers holds for sets of primitive lattice points of the form
$\unicode[STIX]{x1D6E5}\backslash \text{SL}(n+1,\mathbb{R})$ when embedded on expanding horospheres as done in previous work by Marklof. For each of the Farey sequence subsets, we extend the statistical results by Marklof regarding the full multidimensional Farey sequences, and solutions by Athreya and Ghosh to Diophantine approximation problems of Erdős–Szüsz–Turán and Kesten. We also prove that Marklof’s result on the asymptotic distribution of Frobenius numbers holds for sets of primitive lattice points of the form 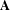 $\mathbf{A}$ .
$\mathbf{A}$ .
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 3
- Cited by


