Article contents
Dynamics of induced systems
Published online by Cambridge University Press: 12 May 2016
Abstract
In this paper we study the dynamical properties of actions on the space of compact subsets of the phase space. More precisely, if 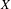 $X$ is a metric space, let
$X$ is a metric space, let 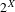 $2^{X}$ denote the space of non-empty compact subsets of
$2^{X}$ denote the space of non-empty compact subsets of 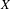 $X$ provided with the Hausdorff topology. If
$X$ provided with the Hausdorff topology. If 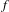 $f$ is a continuous self-map on
$f$ is a continuous self-map on 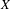 $X$ , there is a naturally induced continuous self-map
$X$ , there is a naturally induced continuous self-map 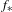 $f_{\ast }$ on
$f_{\ast }$ on 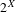 $2^{X}$ . Our main theme is the interrelation between the dynamics of
$2^{X}$ . Our main theme is the interrelation between the dynamics of 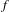 $f$ and
$f$ and  $f_{\ast }$ . For such a study, it is useful to consider the space
$f_{\ast }$ . For such a study, it is useful to consider the space 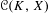 ${\mathcal{C}}(K,X)$ of continuous maps from a Cantor set
${\mathcal{C}}(K,X)$ of continuous maps from a Cantor set 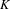 $K$ to
$K$ to 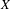 $X$ provided with the topology of uniform convergence, and
$X$ provided with the topology of uniform convergence, and 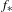 $f_{\ast }$ induced on
$f_{\ast }$ induced on 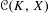 ${\mathcal{C}}(K,X)$ by composition of maps. We mainly study the properties of transitive points of the induced system
${\mathcal{C}}(K,X)$ by composition of maps. We mainly study the properties of transitive points of the induced system 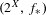 $(2^{X},f_{\ast })$ both topologically and dynamically, and give some examples. We also look into some more properties of the system
$(2^{X},f_{\ast })$ both topologically and dynamically, and give some examples. We also look into some more properties of the system 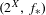 $(2^{X},f_{\ast })$ .
$(2^{X},f_{\ast })$ .
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 12
- Cited by

