Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-26T00:38:22.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous orbit equivalence of topological Markov shifts and dynamical zeta functions

Published online by Cambridge University Press:  06 February 2015

KENGO MATSUMOTO  and
HIROKI MATUI
KENGO MATSUMOTO
Affiliation:
Department of Mathematics, Joetsu University of Education, Joetsu, Niigata 943-8512, Japan email kengo@juen.ac.jp
HIROKI MATUI
Affiliation:
Graduate School of Science, Chiba University, Inage-ku, Chiba 263-8522, Japan email matui@math.s.chiba-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

For continuously orbit equivalent one-sided topological Markov shifts 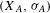$(X_{A},{\it\sigma}_{A})$ and 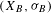$(X_{B},{\it\sigma}_{B})$, their eventually periodic points and cocycle functions are studied. As a result, we directly construct an isomorphism between their ordered cohomology groups 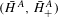$(\bar{H}^{A},\bar{H}_{+}^{A})$ and 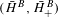$(\bar{H}^{B},\bar{H}_{+}^{B})$. We also show that the cocycle functions for the continuous orbit equivalences give rise to positive elements of their ordered cohomology groups, so that the zeta functions of continuously orbit equivalent topological Markov shifts are related. The set of Borel measures is shown to be invariant under continuous orbit equivalence of one-sided topological Markov shifts.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1557 - 1581
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Boyle, M. and Handelman, D.. Orbit equivalence, flow equivalence and ordered cohomology. Israel J. Math. 95 (1996), 169–210.Google Scholar
Cuntz, J. and Krieger, W.. A class of C ∗ -algebras and topological Markov chains. Invent. Math. 56(3) (1980), 251–268.Google Scholar
Huang, D.. Flow equivalence of reducible shifts of finite type. Ergod. Th. & Dynam. Sys. 14(04) (1994), 695–720.CrossRefGoogle Scholar
Huang, D.. Flow equivalence of reducible shifts of finite type and Cuntz–Krieger algebras. J. Reine Angew. Math. 462 (1995), 185–217.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Matsumoto, K.. Orbit equivalence of topological Markov shifts and Cuntz–Krieger algebras. Pacific J. Math. 246(1) (2010), 199–225.CrossRefGoogle Scholar
Matsumoto, K.. Classification of Cuntz–Krieger algebras by orbit equivalence of topological Markov shifts. Proc. Amer. Math. Soc. 141(7) (2013), 2329–2342.CrossRefGoogle Scholar
Matsumoto, K. and Matui, H.. Continuous orbit equivalence of topological Markov shifts and Cuntz–Krieger algebras. Kyoto J. Math. to appear, arXiv:1307.1299.Google Scholar
Matui, H.. Homology and topological full groups of étale groupoids on totally disconnected spaces. Proc. Lond. Math. Soc. 104(1) (2012), 27–56.Google Scholar
Matui, H.. Topological full groups of one-sided shifts of finite type. J. Reine Angew. Math. to appear,arXiv:1210.5800.Google Scholar
Morita, T.. Meromorphic extensions of a class of dynamical zeta functions and their special values at the origin. Ergod. Th. & Dynam. Sys. 26(04) (2006), 1127–1158.Google Scholar
Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990).Google Scholar
Parry, W. and Sullivan, D.. A topological invariant for flows on one-dimensional spaces. Topology 14(4) (1975), 297–299.Google Scholar
Poon, Y. T.. A K-theoretic invariant for dynamical systems. Trans. Amer. Math. Soc. 311(2) (1989), 515–533.Google Scholar
Renault, J.. A groupoid approach to C ∗ -algebras (Lecture Notes in Mathematics, 793) . Springer, Berlin, Heidelberg and New York, 1980.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic formalism. Addison-Wesley, Reading, MA, 1978.Google Scholar
Ruelle, D.. Dynamical zeta functions and transfer operators. Notices Amer. Math. Soc. 49(8) (2002), 887–895.Google Scholar
Rørdam, M.. Classification of Cuntz–Krieger algebras. K-theory 9(1) (1995), 31–58.Google Scholar