Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T00:32:45.900Z Has data issue: false hasContentIssue false
  • English
  • Français

The contact property for symplectic magnetic fields on 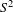$S^{2}$

Published online by Cambridge University Press:  10 November 2014

GABRIELE BENEDETTI
GABRIELE BENEDETTI*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, CB3 0WB, UK email G.Benedetti@dpmms.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we give some positive and negative results about the contact property for the energy levels ${\rm\Sigma}_{c}$ of a symplectic magnetic field on 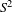$S^{2}$. In the first part we focus on the case of the area form on a surface of revolution. We state a sufficient condition for an energy level to be of contact type and give an example where the contact property fails. If the magnetic curvature is positive, the dynamics and the action of invariant measures can be numerically computed. The collected data hint at the conjecture that an energy level of a symplectic magnetic field with positive magnetic curvature should be of contact type. In the second part we show that, for a small energy $c$, there exist a convex hypersurface 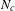$N_{c}$ in 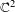$\mathbb{C}^{2}$ and a double cover 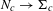$N_{c}\rightarrow {\rm\Sigma}_{c}$ such that the pull-back of the characteristic distribution on 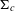${\rm\Sigma}_{c}$ is the standard characteristic distribution on 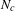$N_{c}$. As a corollary, we prove that there are either two or infinitely many periodic orbits on 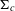${\rm\Sigma}_{c}$. The second alternative holds if there exists a contractible prime periodic orbit.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 3 , May 2016 , pp. 682 - 713
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abraham, R. and Marsden, J. E.. Foundations of Mechanics, 2nd edn. Benjamin/Cummings Advanced Book Program, Reading, MA, 1978.Google Scholar
Bahri, A. and Taĭmanov, I. A.. Periodic orbits in magnetic fields and Ricci curvature of Lagrangian systems. Trans. Amer. Math. Soc. 350(7) (1998), 2697–2717.Google Scholar
Boothby, W. M.. An Introduction to Differentiable Manifolds and Riemannian Geometry (Pure and Applied Mathematics, 120), 2nd edn. Academic Press, Orlando, FL, 1986.Google Scholar
Boothby, W. M. and Wang, H. C.. On contact manifolds. Ann. of Math. (2) 68 (1958), 721–734.CrossRefGoogle Scholar
Brouwer, L. E. J.. Beweis des ebenen Translationssatzes. Math. Ann. 72(1) (1912), 37–54.Google Scholar
Cieliebak, K., Ginzburg, V. L. and Kerman, E.. Symplectic homology and periodic orbits near symplectic submanifolds. Comment. Math. Helv. 79(3) (2004), 554–581.CrossRefGoogle Scholar
Contreras, G.. The Palais–Smale condition on contact type energy levels for convex Lagrangian systems. Calc. Var. Partial Differential Equations 27(3) (2006), 321–395.Google Scholar
Contreras, G., Iturriaga, R., Paternain, G. P. and Paternain, M.. Lagrangian graphs, minimizing measures and Mañé’s critical values. Geom. Funct. Anal. 8(5) (1998), 788–809.Google Scholar
Contreras, G., Macarini, L. and Paternain, G. P.. Periodic orbits for exact magnetic flows on surfaces. Int. Math. Res. Not. 8 (2004), 361–387.Google Scholar
Contreras, G. and Oliveira, F.. C 2 densely the 2-sphere has an elliptic closed geodesic. Ergod. Th. & Dynam. Sys. 24(5) (2004), 1395–1423.Google Scholar
Cristofaro-Gardiner, D. and Hutchings, M.. From one Reeb orbit to two. Preprint, 2012, arXiv:1202.4839.Google Scholar
Eliashberg, Y.. Three lectures on symplectic topology in Cala Gonone. Basic notions, problems and some methods. Rend. Sem. Fac. Sci. Univ. Cagliari 58(suppl) (1988), 27–49.Google Scholar
Eliashberg, Y.. Contact 3-manifolds twenty years since J. Martinet’s work. Ann. Inst. Fourier (Grenoble) 42(1–2) (1992), 165–192.CrossRefGoogle Scholar
Etnyre, J. B.. Tight contact structures on lens spaces. Commun. Contemp. Math. 2(4) (2000), 559–577.Google Scholar
Franks, J.. Geodesics on S 2 and periodic points of annulus homeomorphisms. Invent. Math. 108(2) (1992), 403–418.CrossRefGoogle Scholar
Franks, J.. Area preserving homeomorphisms of open surfaces of genus zero. New York J. Math. 2 (1996), 1–19 (electronic).Google Scholar
Frauenfelder, U., Merry, W. J. and Paternain, G. P.. Floer homology for magnetic fields with at most linear growth on the universal cover. J. Funct. Anal. 262(7) (2012), 3062–3090.Google Scholar
Frauenfelder, U., Merry, W. J. and Paternain, G. P.. Floer homology for non-resonant magnetic fields on flat tori. Preprint, 2013, arXiv:1305.3141.Google Scholar
Frauenfelder, U. and Schlenk, F.. Hamiltonian dynamics on convex symplectic manifolds. Israel J. Math. 159 (2007), 1–56.CrossRefGoogle Scholar
Ginzburg, V. L.. On closed trajectories of a charge in a magnetic field. An application of symplectic geometry. Contact and Symplectic Geometry (Cambridge, 1994) (Publications of the Newton Institute, 8). Cambridge University Press, Cambridge, 1996, pp. 131–148.Google Scholar
Ginzburg, V. L. and Gürel, B. Z.. Relative Hofer–Zehnder capacity and periodic orbits in twisted cotangent bundles. Duke Math. J. 123(1) (2004), 1–47.Google Scholar
Ginzburg, V. L. and Gürel, B. Z.. Periodic orbits of twisted geodesic flows and the Weinstein–Moser theorem. Comment. Math. Helv. 84(4) (2009), 865–907.Google Scholar
Ginzburg, V. L. and Kerman, E.. Periodic orbits in magnetic fields in dimensions greater than two. Geometry and Topology in Dynamics (Winston-Salem, NC, 1998/San Antonio, TX, 1999) (Contemporary Mathematics, 246). American Mathematical Society, Providence, RI, 1999, pp. 113–121.Google Scholar
Ginzburg, V. L. and Kerman, E.. Periodic orbits of Hamiltonian flows near symplectic extrema. Pacific J. Math. 206(1) (2002), 69–91.Google Scholar
Gromov, M.. Pseudoholomorphic curves in symplectic manifolds. Invent. Math. 82(2) (1985), 307–347.CrossRefGoogle Scholar
Guillemin, V.. The Radon transform on Zoll surfaces. Adv. Math. 22(1) (1976), 85–119.Google Scholar
Harris, A. and Paternain, G. P.. Dynamically convex Finsler metrics and J-holomorphic embedding of asymptotic cylinders. Ann. Global Anal. Geom. 34(2) (2008), 115–134.Google Scholar
Hofer, H. and Kriener, M.. Holomorphic curves in contact dynamics. Differential Equations: La Pietra 1996 (Florence) (Proceedings of Symposia in Pure Mathematics, 65). American Mathematical Society, Providence, RI, 1999, pp. 77–131.Google Scholar
Hofer, H., Wysocki, K. and Zehnder, E.. The dynamics on three-dimensional strictly convex energy surfaces. Ann. of Math. (2) 148(1) (1998), 197–289.Google Scholar
Hryniewicz, U., Licata, J. and Salomão, P.. A dynamical characterization of universally tight lens spaces. Proc. Lond. Math. Soc., to appear. Preprint, 2013, arXiv:1306.6617.Google Scholar
Hryniewicz, U. and Salomão, P.. Global properties of tight Reeb flows with applications to Finsler geodesic flows on S 2. Math. Proc. Cambridge Philos. Soc. 154(1) (2012), 1–27.Google Scholar
Kerman, E.. Periodic orbits of Hamiltonian flows near symplectic critical submanifolds. Int. Math. Res. Not. 17 (1999), 953–969.Google Scholar
Kerman, E.. Squeezing in Floer theory and refined Hofer–Zehnder capacities of sets near symplectic submanifolds. Geom. Topol. 9 (2005), 1775–1834.Google Scholar
Koh, D.. On the evolution equation for magnetic geodesics. Calc. Var. Partial Differential Equations 36(3) (2009), 453–480.CrossRefGoogle Scholar
Lu, G.. Finiteness of the Hofer–Zehnder capacity of neighborhoods of symplectic submanifolds. Int. Math. Res. Not. 2006 (2006), Art. ID 76520, 1–33 (electronic).Google Scholar
Macarini, L.. Hofer–Zehnder semicapacity of cotangent bundles and symplectic submanifolds. Preprint, 2003, arXiv:math/0303230.Google Scholar
Macarini, L.. Hofer–Zehnder capacity and Hamiltonian circle actions. Commun. Contemp. Math. 6(6) (2004), 913–945.Google Scholar
McDuff, D.. Applications of convex integration to symplectic and contact geometry. Ann. Inst. Fourier (Grenoble) 37(1) (1987), 107–133.Google Scholar
Merry, W. J.. Closed orbits of a charge in a weakly exact magnetic field. Pacific J. Math. 247(1) (2010), 189–212.Google Scholar
Osuna, O.. Periodic orbits of weakly exact magnetic flows. Preprint, 2005.Google Scholar
Paternain, G. P.. Magnetic rigidity of horocycle flows. Pacific J. Math. 225(2) (2006), 301–323.Google Scholar
Polterovich, L.. Geometry on the group of Hamiltonian diffeomorphisms. Proceedings of the International Congress of Mathematicians. Deutsche Mathematiker Vereinigung, Berlin, 1998, Vol. II (Extra Vol. II) pp. 401–410 (electronic).Google Scholar
Rabinowitz, P. H.. Periodic solutions of Hamiltonian systems. Comm. Pure Appl. Math. 31(2) (1978), 157–184.Google Scholar
Rabinowitz, P. H.. Periodic solutions of a Hamiltonian system on a prescribed energy surface. J. Differential Equations 33(3) (1979), 336–352.Google Scholar
Schlenk, F.. Applications of Hofer’s geometry to Hamiltonian dynamics. Comment. Math. Helv. 81(1) (2006), 105–121.Google Scholar
Schneider, M.. Closed magnetic geodesics on S 2. J. Differential Geom. 87(2) (2011), 343–388.CrossRefGoogle Scholar
Schneider, M.. Alexandrov embedded closed magnetic geodesics on S 2. Ergod. Th. & Dynam. Sys. 32(4) (2012), 1471–1480.Google Scholar
Schneider, M.. Closed magnetic geodesics on closed hyperbolic Riemann surfaces. Proc. Lond. Math. Soc. (3) 105(2) (2012), 424–446.Google Scholar
Taĭmanov, I. A.. Closed extremals on two-dimensional manifolds. Uspekhi Mat. Nauk 47(2(284)) (1992), 143–185, 223.Google Scholar
Taĭmanov, I. A.. Periodic magnetic geodesics on almost every energy level via variational methods. Regul. Chaotic Dyn. 15(4–5) (2010), 598–605.Google Scholar
Taubes, C. H.. The Seiberg–Witten equations and the Weinstein conjecture. Geom. Topol. 11 (2007), 2117–2202.Google Scholar
Usher, M.. Floer homology in disk bundles and symplectically twisted geodesic flows. J. Mod. Dyn. 3(1) (2009), 61–101.Google Scholar
Weinstein, A.. Fourier integral operators, quantization, and the spectra of Riemannian manifolds. Géométrie symplectique et physique mathématique (Colloque International du CNRS, No. 237, Aix-en-Provence, 1974). Éditions du Centre National de la Recherche Scientifique, Paris, 1975, pp. 289–298. With questions by W. Klingenberg and K. Bleuler and replies by the author.Google Scholar
Weinstein, A.. Periodic orbits for convex Hamiltonian systems. Ann. of Math. (2) 108(3) (1978), 507–518.Google Scholar
Weinstein, A.. On the hypotheses of Rabinowitz’ periodic orbit theorems. J. Differential Equations 33(3) (1979), 353–358.Google Scholar