Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-25T08:16:07.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditions for equality between Lyapunov and Morse decompositions

Published online by Cambridge University Press:  08 January 2015

LUCIANA A. ALVES  and
LUIZ A. B. SAN MARTIN
LUCIANA A. ALVES
Affiliation:
Faculdade de Matemática – Universidade Federal de Uberlândia, Campus Santa Mônica, Av. João Naves de Ávila, 2121, 38408-100 Uberlândia – MG, Brasil email lualves@famat.ufu.br
LUIZ A. B. SAN MARTIN
Affiliation:
Imecc – Unicamp, Departamento de Matemática, Rua Sérgio Buarque de Holanda, 651, Cidade Universitária Zeferino Vaz, 13083-859 Campinas – SP, Brasil email smartin@ime.unicamp.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 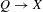$Q\rightarrow X$ be a continuous principal bundle whose group 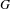$G$ is reductive. A flow 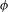${\it\phi}$ of automorphisms of 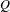$Q$ endowed with an ergodic probability measure on the compact base space 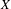$X$ induces two decompositions of the flag bundles associated to $Q$: a continuous one given by the finest Morse decomposition and a measurable one furnished by the multiplicative ergodic theorem. The second is contained in the first. In this paper we find necessary and sufficient conditions so that they coincide. The equality between the two decompositions implies continuity of the Lyapunov spectra under perturbations leaving unchanged the flow on the base space.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1007 - 1036
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alves, L. A. and San Martin, L. A. B.. Multiplicative ergodic theorem on flag bundles of semi-simple Lie groups. Discrete Contin. Dyn. Syst. 33 (2013), 1247–1273.Google Scholar
Bonatti, C., Diaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity (Encyclopedia of Mathematical Sciences, 102). Springer, Berlin, 2005.Google Scholar
Braga Barros, C. J. and San Martin, L. A. B.. Chain transitive sets for flows on flag bundles. Forum Math. 19 (2007), 19–60.Google Scholar
Bronstein, I. U. and Chernii, V. F.. Linear extensions satisfying Perron’s condition I. Differ. Equ. 14 (1978), 1234–1243.Google Scholar
Colonius, F. and Kliemann, W.. The Dynamics of Control. Birkhäuser, Boston, MA, 2000.Google Scholar
Conley, C.. Isolated Invariant Sets and the Morse Index (CBMS Regional Conference Series in Mathematics, 38). American Mathematical Society, Providence, RI, 1978.Google Scholar
Duistermat, J. J., Kolk, J. A. C. and Varadarajan, V. S.. Functions, flows and oscillatory integral on flag manifolds. Compos. Math. 49 (1983), 309–398.Google Scholar
Ferraiol, T., Patrão, M. and Seco, L.. Jordan decomposition and dynamics on flag manifolds. Discrete Contin. Dyn. Syst. 26(3) (2010), 923–947.CrossRefGoogle Scholar
Ferraiol, T. and San Martin, L. A. B.. Differentiability of Lyapunov exponents and Morse decompositions. Preprint, 2014, to appear, arXiv:1405.1262.Google Scholar
Furman, A.. On the multiplicative ergodic theorem for uniquely ergodic systems. Ann. Inst. Henri Poincaré Probab. Stat. 33 (1997), 797–815.Google Scholar
Guivarch’, Y. and Raugi, A.. Frontière de Furstenberg, proprietés de contraction et théorèmes de convergence. Probab. Theory Relat. Top. 69 (1985), 187–242.Google Scholar
Herman, M. R.. Construction d’un diffeomorphisme minimal d’entropie topologique non nulle. Ergod. Th. & Dynam. Sys. 1 (1981), 65–76.Google Scholar
Knapp, A. W.. Lie Groups: Beyond an Introduction (Progress in Mathematics, 140), 2nd edn. Birkhäuser, Basel, 2004.Google Scholar
Mañé, R.. Ergodic Theory and Differentiable Dynamics. Springer, Berlin, 1989.Google Scholar
Patrão, M. and San Martin, L. A. B.. Morse decomposition of semiflows on fiber bundles. Discrete Contin. Dyn. Syst. 17 (2007), 561–587.CrossRefGoogle Scholar
Patrão, M., San Martin, L. A. B. and Seco, L.. Conley indexes and stable sets for flows on flag bundles. Dyn. Syst. 24 (2009), 249–276.Google Scholar
San Martin, L. A. B.. Invariant control sets on flag manifolds. Math. Control Signals Systems 6 (1993), 41–61.CrossRefGoogle Scholar
San Martin, L. A. B.. Maximal semigroups in semi-simple Lie groups. Trans. Amer. Math. Soc. 353 (2001), 5165–5184.Google Scholar
San Martin, L. A. B. and Seco, L.. Morse and Lyapunov spectra and dynamics on flag bundles. Ergod. Th. & Dynam. Sys. 30 (2010), 893–922.Google Scholar
San Martin, L. A. B., Rocio, O. G. and Verdi, M. A.. Semigroup actions on adjoint orbits. J. Lie Theory 22 (2012), 931–948.Google Scholar
Selgrade, J.. Isolated invariant sets for flows on vector bundles. Trans. Amer. Math. Soc. 203 (1975), 259–390.Google Scholar
Warner, G.. Harmonic Analysis on Semi-simple Lie Groups I. Springer, Berlin, 1972.Google Scholar