Article contents
Amenable dynamical systems over locally compact groups
Published online by Cambridge University Press: 25 June 2021
Abstract
We establish several new characterizations of amenable 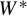 $W^*$- and
$W^*$- and 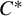 $C^*$-dynamical systems over arbitrary locally compact groups. In the
$C^*$-dynamical systems over arbitrary locally compact groups. In the 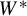 $W^*$-setting we show that amenability is equivalent to (1) a Reiter property and (2) the existence of a certain net of completely positive Herz–Schur multipliers of
$W^*$-setting we show that amenability is equivalent to (1) a Reiter property and (2) the existence of a certain net of completely positive Herz–Schur multipliers of 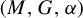 $(M,G,\alpha )$ converging point weak* to the identity of
$(M,G,\alpha )$ converging point weak* to the identity of 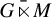 $G\bar {\ltimes }M$. In the
$G\bar {\ltimes }M$. In the 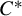 $C^*$-setting, we prove that amenability of
$C^*$-setting, we prove that amenability of 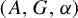 $(A,G,\alpha )$ is equivalent to an analogous Herz–Schur multiplier approximation of the identity of the reduced crossed product
$(A,G,\alpha )$ is equivalent to an analogous Herz–Schur multiplier approximation of the identity of the reduced crossed product 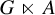 $G\ltimes A$, as well as a particular case of the positive weak approximation property of Bédos and Conti [On discrete twisted
$G\ltimes A$, as well as a particular case of the positive weak approximation property of Bédos and Conti [On discrete twisted 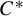 $C^*$-dynamical systems, Hilbert
$C^*$-dynamical systems, Hilbert 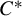 $C^*$-modules and regularity. Münster J. Math. 5 (2012), 183–208] (generalized to the locally compact setting). When
$C^*$-modules and regularity. Münster J. Math. 5 (2012), 183–208] (generalized to the locally compact setting). When  $Z(A^{**})=Z(A)^{**}$, it follows that amenability is equivalent to the 1-positive approximation property of Exel and Ng [Approximation property of
$Z(A^{**})=Z(A)^{**}$, it follows that amenability is equivalent to the 1-positive approximation property of Exel and Ng [Approximation property of 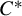 $C^*$-algebraic bundles. Math. Proc. Cambridge Philos. Soc. 132(3) (2002), 509–522]. In particular, when
$C^*$-algebraic bundles. Math. Proc. Cambridge Philos. Soc. 132(3) (2002), 509–522]. In particular, when 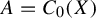 $A=C_0(X)$ is commutative, amenability of
$A=C_0(X)$ is commutative, amenability of 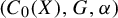 $(C_0(X),G,\alpha )$ coincides with topological amenability of the G-space
$(C_0(X),G,\alpha )$ coincides with topological amenability of the G-space 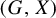 $(G,X)$.
$(G,X)$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 6
- Cited by


