No CrossRef data available.
Article contents
Transcendental Julia sets of minimal Hausdorff dimension
Published online by Cambridge University Press: 06 January 2025
Abstract
We show the existence of transcendental entire functions 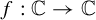 $f: \mathbb {C} \rightarrow \mathbb {C}$ with Hausdorff-dimension
$f: \mathbb {C} \rightarrow \mathbb {C}$ with Hausdorff-dimension 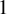 $1$ Julia sets, such that every Fatou component of f has infinite inner connectivity. We also show that there exist singleton complementary components of any Fatou component of f, answering a question of Rippon and Stallard [Eremenko points and the structure of the escaping set. Trans. Amer. Math. Soc. 372(5) (2019), 3083–3111]. Our proof relies on a quasiconformal-surgery approach developed by Burkart and Lazebnik [Interpolation of power mappings. Rev. Mat. Iberoam. 39(3) (2023), 1181–1200].
$1$ Julia sets, such that every Fatou component of f has infinite inner connectivity. We also show that there exist singleton complementary components of any Fatou component of f, answering a question of Rippon and Stallard [Eremenko points and the structure of the escaping set. Trans. Amer. Math. Soc. 372(5) (2019), 3083–3111]. Our proof relies on a quasiconformal-surgery approach developed by Burkart and Lazebnik [Interpolation of power mappings. Rev. Mat. Iberoam. 39(3) (2023), 1181–1200].
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
References
Albrecht, S. and Bishop, C. J.. Speiser class Julia sets with dimension near one. J. Anal. Math. 141(1) (2020), 49–98.CrossRefGoogle Scholar
Astala, K. and Gehring, F. W.. Quasiconformal analogues of theorems of Koebe and Hardy–Littlewood. Michigan Math. J. 32(1) (1985), 99–107.CrossRefGoogle Scholar
Astala, K., Iwaniec, T. and Martin, G.. Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane (Princeton Mathematical Series, 48). Princeton University Press, Princeton, NJ, 2009.Google Scholar
Avila, A. and Lyubich, M.. Lebesgue measure of Feigenbaum Julia sets. Ann. of Math. (2) 195(1) (2022), 1–88.CrossRefGoogle Scholar
Baker, I. N.. The domains of normality of an entire function. Ann. Acad. Sci. Fenn. Ser. A I Math. 1(2) (1975), 277–283.CrossRefGoogle Scholar
Buff, X. and Chéritat, A.. Quadratic Julia sets with positive area. Ann. of Math. (2) 176(2) (2012), 673–746.CrossRefGoogle Scholar
Bergweiler, W.. An entire function with simply and multiply connected wandering domains. Pure Appl. Math. Q. 7(1) (2011), 107–120.CrossRefGoogle Scholar
Bishop, C. J.. A transcendental Julia set of dimension 1. Invent. Math. 212(2) (2018), 407–460.CrossRefGoogle Scholar
Burkart, J. and Lazebnik, K.. Interpolation of power mappings. Rev. Mat. Iberoam. 39(3) (2023), 1181–1200.CrossRefGoogle Scholar
Bergweiler, W., Rippon, P. J. and Stallard, G. M.. Multiply connected wandering domains of entire functions. Proc. Lond. Math. Soc. (3) 107(6) (2013), 1261–1301.CrossRefGoogle Scholar
Benini, A. M., Rippon, P. J. and Stallard, G. M.. Permutable entire functions and multiply connected wandering domains. Adv. Math. 287 (2016), 451–462.CrossRefGoogle Scholar
Burkart, J.. Transcendental Julia sets with fractional packing dimension. Conform. Geom. Dyn. 25 (2021), 200–252.CrossRefGoogle Scholar
Bergweiler, W. and Zheng, J.-H.. On the uniform perfectness of the boundary of multiply connected wandering domains. J. Aust. Math. Soc. 91(3) (2011), 289–311.CrossRefGoogle Scholar
Douady, A. and Hubbard, J. H.. On the dynamics of polynomial-like mappings. Ann. Sci. Éc. Norm. Supér. (4) 18(2) (1985), 287–343.CrossRefGoogle Scholar
Ferreira, G. R.. Multiply connected wandering domains of meromorphic functions: internal dynamics and connectivity. J. Lond. Math. Soc. (2) 106(3) (2022), 1897–1919.CrossRefGoogle Scholar
Fagella, N., Jarque, X. and Lazebnik, K.. Univalent wandering domains in the Eremenko–Lyubich class. J. Anal. Math. 139(1) (2019), 369–395.CrossRefGoogle Scholar
Herring, M. E.. Mapping properties of Fatou components. Ann. Acad. Sci. Fenn. Math. 23(2) (1998), 263–274.Google Scholar
Kisaka, M. and Shishikura, M.. On multiply connected wandering domains of entire functions. Transcendental Dynamics and Complex Analysis (London Mathematical Society Lecture Note Series, 348). Cambridge University Press, Cambridge, 2008.Google Scholar
Lehto, O. and Virtanen, K. I.. Quasiconformal Mappings in the Plane (Die Grundlehren der mathematischen Wissenschaften, 126), 2nd edn. Springer-Verlag, New York, 1973; translated from the German by K. W. Lucas.CrossRefGoogle Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300(1) (1987), 329–342.CrossRefGoogle Scholar
McMullen, C. T.. Complex Dynamics and Renormalization (Annals of Mathematics Studies, 135). Princeton University Press, Princeton, NJ, 1994.Google Scholar
Misiurewicz, M.. On iterates of
 ${e}^z$
. Ergod. Th. & Dynam. Sys. 1(1) (1981), 103–106.CrossRefGoogle Scholar
${e}^z$
. Ergod. Th. & Dynam. Sys. 1(1) (1981), 103–106.CrossRefGoogle Scholar
Rempe-Gillen, L. and Sixsmith, D.. On connected preimages of simply-connected domains under entire functions. Geom. Funct. Anal. 29(5) (2019), 1579–1615.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. On multiply connected wandering domains of meromorphic functions. J. Lond. Math. Soc. (2) 77(2) (2008), 405–423.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. Eremenko points and the structure of the escaping set. Trans. Amer. Math. Soc. 372(5) (2019), 3083–3111.CrossRefGoogle Scholar
Shishikura, M.. The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets. Ann. of Math. (2) 147(2) (1998), 225–267.CrossRefGoogle Scholar
Shishikura, M.. Conformality of quasiconformal mappings at a point, revisited. Ann. Acad. Sci. Fenn. Math. 43(2) (2018), 981–990.CrossRefGoogle Scholar
Stallard, G. M.. The Hausdorff dimension of Julia sets of entire functions. Ergod. Th. & Dynam. Sys. 11(4) (1991), 769–777.CrossRefGoogle Scholar
Stallard, G. M.. The Hausdorff dimension of Julia sets of entire functions. II. Math. Proc. Cambridge Philos. Soc. 119(3) (1996), 513–536.CrossRefGoogle Scholar
Stallard, G. M.. The Hausdorff dimension of Julia sets of entire functions. IV. J. Lond. Math. Soc. (2) 61(2) (2000), 471–488.CrossRefGoogle Scholar
Steinmetz, N.. The formula of Riemann–Hurwitz and iteration of rational functions. Complex Var. Theory Appl. 22(3–4) (1993), 203–206.Google Scholar
Tao, T.. Analysis. II (Texts and Readings in Mathematics, 38), 3rd edn. Hindustan Book Agency, New Delhi, 2014.Google Scholar
Urbański, M.. Rational functions with no recurrent critical points. Ergod. Th. & Dynam. Sys. 14(2) (1994), 391–414.CrossRefGoogle Scholar
Zhang, X.. A generalized family of transcendental functions with one dimensional Julia sets. J. Difference Equ. Appl. 30(2) (2024), 184–232.CrossRefGoogle Scholar


