Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-11T20:10:24.396Z Has data issue: false hasContentIssue false
  • English
  • Français

On invariant subalgebras of group 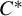$C^*$ and von Neumann algebras

Part of: Selfadjoint operator algebras Locally compact groups and their algebras

Published online by Cambridge University Press:  04 November 2022

MEHRDAD KALANTAR Open the ORCID record for MEHRDAD KALANTAR [Opens in a new window]  and
NIKOLAOS PANAGOPOULOS
MEHRDAD KALANTAR*
Affiliation:
Department of Mathematics, University of Houston, Houston, TX 77004, USA (e-mail: npanagopoulos@uh.edu)
NIKOLAOS PANAGOPOULOS
Affiliation:
Department of Mathematics, University of Houston, Houston, TX 77004, USA (e-mail: npanagopoulos@uh.edu)
*
e-mail: mkalantar@uh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an irreducible lattice 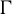$\Gamma $ in the product of higher rank simple Lie groups, we prove a co-finiteness result for the 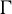$\Gamma $-invariant von Neumann subalgebras of the group von Neumann algebra 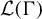$\mathcal {L}(\Gamma )$, and for the 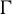$\Gamma $-invariant unital 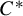$C^*$-subalgebras of the reduced group 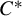$C^*$-algebra 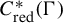$C^*_{\mathrm {red}}(\Gamma )$. We use these results to show that: (i) every 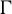$\Gamma $-invariant von Neumann subalgebra of 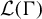$\mathcal {L}(\Gamma )$ is generated by a normal subgroup; and (ii) given a weakly mixing unitary representation 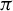$\pi $ of 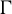$\Gamma $, every 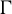$\Gamma $-equivariant conditional expectation on 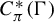$C^*_\pi (\Gamma )$ is the canonical conditional expectation onto the 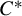$C^*$-subalgebra generated by a normal subgroup.

Keywords

invariant subalgebrasunitary representationslattices

MSC classification

Primary: 22D25: $C^*$-algebras and $W^*$-algebras in relation to group representations
Secondary: 46L40: Automorphisms
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 10 , October 2023 , pp. 3341 - 3353
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseev, V. and Brugger, R.. A rigidity result for normalized subfactors. J. Operator Theory 86(1) (2021), 3–15.CrossRefGoogle Scholar
Anantharaman-Delaroche, C. and Popa, S.. An introduction to $I{I}_1$ factors, in preparation.Google Scholar
Amrutam, T. and Hartman, Y.. Subalgebras, subgroups, and singularity. Preprint, 2022, arXiv:2208.06019.Google Scholar
Amrutam, T. and Jiang, Y.. On invariant von Neumann subalgebras rigidity property. Preprint, 2022, arXiv:2205.10700.CrossRefGoogle Scholar
Arveson, W. B.. Subalgebras of ${C}^{\ast }$ -algebras. Acta Math. 123 (1969), 141–224.CrossRefGoogle Scholar
Bader, U., Boutonnet, R. and Houdayer, C.. Charmenability of higher rank arithmetic groups. Preprint, 2021, arXiv:2112.01337.Google Scholar
Bader, U., Boutonnet, R., Houdayer, C. and Peterson, J.. Charmenability of arithmetic groups of product type. Invent. Math. 229 (2022), 929–985.Google Scholar
Bekka, B., Cowling, M. and de la Harpe, P.. Some groups whose reduced ${C}^{\ast }$ -algebra is simple. Publ. Math. Inst. Hautes Études Sci. 80 (1994), 117–134 (1995).CrossRefGoogle Scholar
Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property $({\textit{T}})$ (New Mathematical Monographs, 11). Cambridge University Press, Cambridge, 2008.Google Scholar
Bekka, B.. Amenable unitary representations of locally compact groups. Invent. Math. 100(2) (1990), 383–401.CrossRefGoogle Scholar
Bekka, B.. Operator-algebraic superridigity for ${SL}_n\kern-1pt(\mathbb{Z})$ , $n\ge 3$ . Invent. Math. 169(2) (2007), 401–425.CrossRefGoogle Scholar
Boutonnet, R. and Houdayer, C.. Stationary characters on lattices of semisimple Lie groups. Publ. Math. Inst. Hautes Études Sci. 133 (2021), 1–46.CrossRefGoogle Scholar
Boutonnet, R., Ioana, A. and Peterson, J.. Properly proximal groups and their von Neumann algebras. Ann. Sci. Éc. Norm. Supér. (4) 54(2) (2021), 445–482 (English, with English and French summaries).CrossRefGoogle Scholar
Breuillard, E., Kalantar, M., Kennedy, M. and Ozawa, N.. ${C}^{\ast }$ -simplicity and the unique trace property for discrete groups. Publ. Math. Inst. Hautes Études Sci. 126 (2017), 35–71.CrossRefGoogle Scholar
Brugger, R.. Characters on infinite groups and rigidity. PhD Dissertation, Georg-August University of Göttingen, 2018.Google Scholar
Bader, U. and Shalom, Y.. Factor and normal subgroup theorems for lattices in products of groups. Invent. Math. 163(2) (2006), 415–454.CrossRefGoogle Scholar
Bekka, B. and Valette, A.. Kazhdan’s property $({\textit{T}})$ and amenable representations. Math. Z. 212(2) (1993), 293–299.CrossRefGoogle Scholar
Chifan, I. and Das, S.. Rigidity results for von Neumann algebras arising from mixing extensions of profinite actions of groups on probability spaces. Math. Ann. 378(3–4) (2020), 907–950.CrossRefGoogle Scholar
Chifan, I., Das, S. and Sun, B.. Invariant subalgebras of von Neumann algebras arising from negatively curved groups. Preprint, 2022, arXiv:2207.13775.CrossRefGoogle Scholar
Choda, M.. Group factors of the Haagerup type. Proc. Japan Acad. Ser. A Math. Sci. 59(5) (1983), 174–177.CrossRefGoogle Scholar
Dong, Z.. Haagerup property for ${C}^{\ast }$ -algebras. J. Math. Anal. Appl. 377(2) (2011), 631–644.CrossRefGoogle Scholar
Das, S. and Peterson, J.. Poisson boundaries of II1 factors. Preprint, 2022, arXiv:2009.11787.CrossRefGoogle Scholar
Furman, A.. On minimal strongly proximal actions of locally compact groups. Israel J. Math. 136 (2003), 173–187.CrossRefGoogle Scholar
Furstenberg, H.. Poisson boundaries and envelopes of discrete groups. Bull. Amer. Math. Soc. (N.S.) 73 (1967), 350–356.CrossRefGoogle Scholar
Grigorchuk, R., Musat, M. and Rørdam, M.. Just-infinite ${C}^{\ast }$ -algebras. Comment. Math. Helv. 93(1) (2018), 157–201.CrossRefGoogle Scholar
Haagerup, U.. The standard form of von Neumann algebras. Math. Scand. 37(2) (1975), 271–283.CrossRefGoogle Scholar
Hamana, M.. Injective envelopes of C*-dynamical systems. Tohoku Math. J. (2) 37 (1985), 463–487.CrossRefGoogle Scholar
Hartman, Y. and Kalantar, M.. Stationary ${C}^{\ast }$ -dynamical systems. J. Eur. Math. Soc. (JEMS), to appear.Google Scholar
Izumi, M.. Non-commutative Poisson boundaries. Discrete Geometric Analysis (Contemporary Mathematics, 347). American Mathematical Society, Providence, RI, 2004, pp. 69–81.CrossRefGoogle Scholar
Jones, V. F. R.. Index for subfactors. Invent. Math. 72(1) (1983), 1–25.CrossRefGoogle Scholar
Le Boudec, A.. ${C}^{\ast }$ -simplicity and the amenable radical. Invent. Math. 209(1) (2017), 159–174.CrossRefGoogle Scholar
Margulis, G. A.. Discrete Subgroups of Semisimple Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 17). Springer-Verlag, Berlin, 1991.CrossRefGoogle Scholar
Okayasu, R. and Tomatsu, R.. Haagerup approximation property for arbitrary von Neumann algebras. Publ. Res. Inst. Math. Sci. 51(3) (2015), 567–603.CrossRefGoogle Scholar
Peterson, J.. Character rigidity for lattices in higher-rank groups. Preprint, 2015.Google Scholar
Popa, S.. On the relative Dixmier property for inclusions of ${C}^{\ast }$ -algebras. J. Funct. Anal. 171(1) (2000), 139–154.CrossRefGoogle Scholar
Suzuki, Y.. Haagerup property for ${C}^{\ast }$ -algebras and rigidity of ${C}^{\ast }$ -algebras with property $({\textit{T}})$ . J. Funct. Anal. 265(8) (2013), 1778–1799.CrossRefGoogle Scholar
Stuck, G. and Zimmer, R. J.. Stabilizers for ergodic actions of higher rank semisimple groups. Ann. of Math. (2) 139(3) (1994), 723–747.CrossRefGoogle Scholar