Article contents
On higher-order Fourier analysis in characteristic p
Published online by Cambridge University Press: 27 January 2023
Abstract
In this paper, the nilspace approach to higher-order Fourier analysis is developed in the setting of vector spaces over a prime field 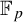 $\mathbb {F}_p$, with applications mainly in ergodic theory. A key requisite for this development is to identify a class of nilspaces adequate for this setting. We introduce such a class, whose members we call p-homogeneous nilspaces. One of our main results characterizes these objects in terms of a simple algebraic property. We then prove various further results on these nilspaces, leading to a structure theorem describing every finite p-homogeneous nilspace as the image, under a nilspace fibration, of a member of a simple family of filtered finite abelian p-groups. The applications include a description of the Host–Kra factors of ergodic
$\mathbb {F}_p$, with applications mainly in ergodic theory. A key requisite for this development is to identify a class of nilspaces adequate for this setting. We introduce such a class, whose members we call p-homogeneous nilspaces. One of our main results characterizes these objects in terms of a simple algebraic property. We then prove various further results on these nilspaces, leading to a structure theorem describing every finite p-homogeneous nilspace as the image, under a nilspace fibration, of a member of a simple family of filtered finite abelian p-groups. The applications include a description of the Host–Kra factors of ergodic 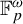 $\mathbb {F}_p^\omega $-systems as p-homogeneous nilspace systems. This enables the analysis of these factors to be reduced to the study of such nilspace systems, with central questions on the factors thus becoming purely algebraic problems on finite nilspaces. We illustrate this approach by proving that for
$\mathbb {F}_p^\omega $-systems as p-homogeneous nilspace systems. This enables the analysis of these factors to be reduced to the study of such nilspace systems, with central questions on the factors thus becoming purely algebraic problems on finite nilspaces. We illustrate this approach by proving that for 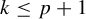 $k\leq p+1$ the kth Host–Kra factor is an Abramov system of order at most k, extending a result of Bergelson–Tao–Ziegler that holds for
$k\leq p+1$ the kth Host–Kra factor is an Abramov system of order at most k, extending a result of Bergelson–Tao–Ziegler that holds for 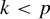 $k< p$. We illustrate the utility of p-homogeneous nilspaces also by showing that the structure theorem yields a new proof of the Tao–Ziegler inverse theorem for Gowers norms on
$k< p$. We illustrate the utility of p-homogeneous nilspaces also by showing that the structure theorem yields a new proof of the Tao–Ziegler inverse theorem for Gowers norms on 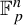 $\mathbb {F}_p^n$.
$\mathbb {F}_p^n$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by


