Article contents
Dynamical behavior of alternate base expansions
Published online by Cambridge University Press: 22 December 2021
Abstract
We generalize the greedy and lazy 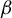 $\beta $-transformations for a real base
$\beta $-transformations for a real base 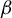 $\beta $ to the setting of alternate bases
$\beta $ to the setting of alternate bases 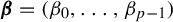 ${\boldsymbol {\beta }}=(\beta _0,\ldots ,\beta _{p-1})$, which were recently introduced by the first and second authors as a particular case of Cantor bases. As in the real base case, these new transformations, denoted
${\boldsymbol {\beta }}=(\beta _0,\ldots ,\beta _{p-1})$, which were recently introduced by the first and second authors as a particular case of Cantor bases. As in the real base case, these new transformations, denoted 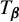 $T_{{\boldsymbol {\beta }}}$ and
$T_{{\boldsymbol {\beta }}}$ and 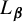 $L_{{\boldsymbol {\beta }}}$ respectively, can be iterated in order to generate the digits of the greedy and lazy
$L_{{\boldsymbol {\beta }}}$ respectively, can be iterated in order to generate the digits of the greedy and lazy 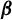 ${\boldsymbol {\beta }}$-expansions of real numbers. The aim of this paper is to describe the measure-theoretical dynamical behaviors of
${\boldsymbol {\beta }}$-expansions of real numbers. The aim of this paper is to describe the measure-theoretical dynamical behaviors of 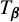 $T_{{\boldsymbol {\beta }}}$ and
$T_{{\boldsymbol {\beta }}}$ and 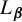 $L_{{\boldsymbol {\beta }}}$. We first prove the existence of a unique absolutely continuous (with respect to an extended Lebesgue measure, called the p-Lebesgue measure)
$L_{{\boldsymbol {\beta }}}$. We first prove the existence of a unique absolutely continuous (with respect to an extended Lebesgue measure, called the p-Lebesgue measure) 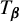 $T_{{\boldsymbol {\beta }}}$-invariant measure. We then show that this unique measure is in fact equivalent to the p-Lebesgue measure and that the corresponding dynamical system is ergodic and has entropy
$T_{{\boldsymbol {\beta }}}$-invariant measure. We then show that this unique measure is in fact equivalent to the p-Lebesgue measure and that the corresponding dynamical system is ergodic and has entropy 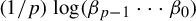 $({1}/{p})\log (\beta _{p-1}\cdots \beta _0)$. We give an explicit expression of the density function of this invariant measure and compute the frequencies of letters in the greedy
$({1}/{p})\log (\beta _{p-1}\cdots \beta _0)$. We give an explicit expression of the density function of this invariant measure and compute the frequencies of letters in the greedy 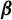 ${\boldsymbol {\beta }}$-expansions. The dynamical properties of
${\boldsymbol {\beta }}$-expansions. The dynamical properties of 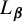 $L_{{\boldsymbol {\beta }}}$ are obtained by showing that the lazy dynamical system is isomorphic to the greedy one. We also provide an isomorphism with a suitable extension of the
$L_{{\boldsymbol {\beta }}}$ are obtained by showing that the lazy dynamical system is isomorphic to the greedy one. We also provide an isomorphism with a suitable extension of the 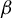 $\beta $-shift. Finally, we show that the
$\beta $-shift. Finally, we show that the 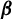 ${\boldsymbol {\beta }}$-expansions can be seen as
${\boldsymbol {\beta }}$-expansions can be seen as  $(\beta _{p-1}\cdots \beta _0)$-representations over general digit sets and we compare both frameworks.
$(\beta _{p-1}\cdots \beta _0)$-representations over general digit sets and we compare both frameworks.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by


